一种基于星载氢钟误差信号提取的实现方法

赵广东， 陈鹏飞， 刘 杰， 黄 奕， 李思衡

(1. 上海航天电子技术研究所，上海 201109；2. 中国科学院上海天文台，上海 200030)

1 引 言

卫星导航定位系统实际上是卫星测距和定时系统。无论在星上或者地面的主控站或监测站都需要有高精度的原子钟。被动型星载氢原子钟作为星载原子钟的一个分类，可适用于配置我国自主研发的导航组网卫星，提供高精度时间和频率基准。该系统主要为各类用户提供定位、导航、测速、授时和通信等服务，且系统的时间基准信号的稳定性及漂移率对系统的定位精度有着决定性的影响。目前国际上只有欧洲的伽利略卫星导航系统以及我国的北斗卫星系统配备了星载氢原子钟。目前星载氢原子钟的指标可以达到频率准确度≤±5×10-12，秒稳定度≤1×10-12，万秒稳定度≤1×10-14，天稳定度≤7×10-15，频率漂移率≤1×10-14/天。

被动型星载氢原子钟有单频以及双频两种工作模式，单频电路采用一种调制频率，实现对微波腔和晶振信号的复用控制，完成系统闭环；与之相对，双频电路采用两种探测频率，分时对微波腔和晶振信号进行闭环控制。相比之下，双频电路在长期稳定性指标和温度系数等方面较容易控制。本文讨论了被动型星载氢钟电路系统双频方案中，如何从物理部分调制信号中提取检出微波腔及晶振的分时误差信号，并通过模拟开关实现误差信号分离，分别送入AD模数转换器数字采样，实现误差闭环控制，并最终实现微波腔及原子信号的锁定。本研究探讨的是如何将其中两路误差调制信号进行包络检波解调的实现方法。

2 原理分析

被动型星载氢原子钟与主动型原子钟的工作原理差异在于其需要电路系统给物理系统外部激励信号，激发内部提纯出来的氢原子跃迁，对跃迁出来的信号进行误差提取、分离，通过PID算法，实现对误差量的控制，从而实现原子钟的锁定。原理示意图如图1所示。

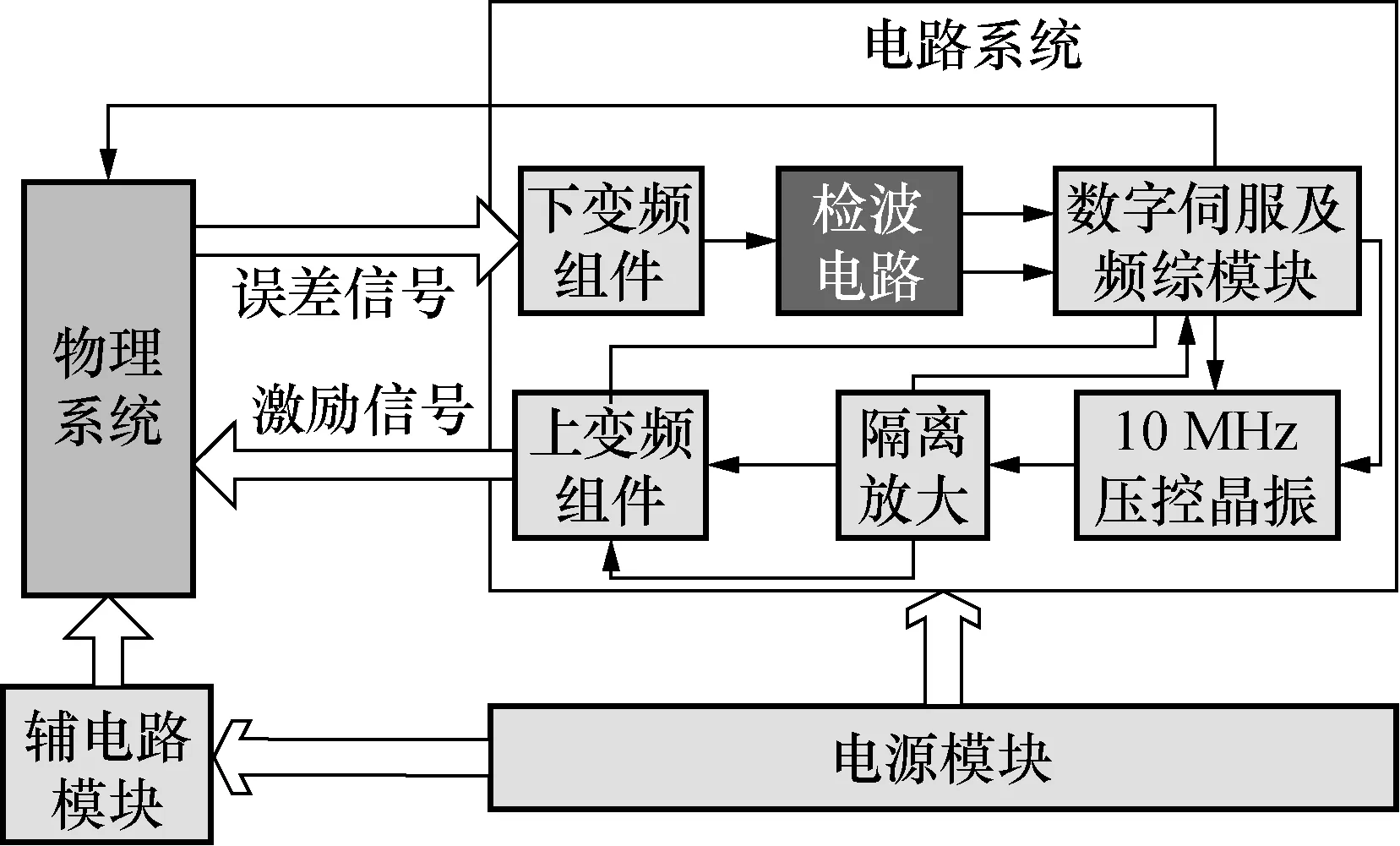
图1 被动型星载氢原子钟原理框图Fig.1 Functional block diagram of the space-borne hydrogen atomic clock

2.1 探测信号分析

被动型星载氢原子钟的双频实现方案中，假设晶振探测信号的中心频点为f0，微波腔探测信号的中心频点为f1，在一个T时间探测周期内，对氢原子的探测时间为T1，对微波腔的探测时间为T2。在T1时间内，以探测信号中心f0为基准，实现f0+fc与f0-fc的频点跳变，跳变周期为t1；进入T2时间后，以探测信号中心f1为基准，实现f1+fd与f1-fd的频点跳变，跳变周期为t2。T2时间结束后，重新进入T1时间循环激励。一般情况下，探测信号的频率综合输出，令f0=f1，下文均用f0来表示探测信号中心频点。其中，f0初始理论值为1 420.405 751 MHz，fc=12.5 Hz，fd=50 kHz；T1=4.04 s，T2=400 ms，t1=t2=40 ms；

星载氢原子钟物理腔激励信号按上述周期交替馈入物理腔，持续探测物理微波腔以及氢原子的能级跃迁信号。经过伺服控制电路分别反馈控制物理变容二极管容值以及晶振压控电压后，探测信号频率进入可控范围，微波腔幅度调制的误差信号以及电路系统的恒温晶振的误差信号逐渐变得清晰，直至可以被系统解调并通过相应的反馈通道控制并锁定。

物理系统的微波腔可以看作带宽很窄的门限滤波器，周期内的探测信号通过后形成了调幅波，当微波腔中心频点与f0存在频率差，则微波腔的探测输出信号在T2时间内，存在+fd与-fd的相邻跳频时间内的信号幅度差，经过包络检波后获取的就是其误差信号，当该误差信号进入一定范围内后即可经过比例积分运算后经过内部的变容二极管进行调整，从而将微波腔的中心频点最终锁定在系统需要的频点上。

同上，当探测信号f0+fc与f0-fc相邻周期的信号进入氢原子跃迁条件的误差范围内后，原子跃迁的误差信息经过包络检波后获取，同样经过比例积分运算后反馈至恒温晶振的压控电压端调整晶振的输出频率，最终消除了相邻周期的探测误差，实现晶振输出频率锁定在氢原子的跃迁频率上。

被动型氢钟的探测信号用指数形式表示的函数Ainc如下。令：

Ainc=A0exp{i{[ω0+φc(t)]t}}

(1)

则：

Ainc=A0exp{i[ω0t+mg(t)]}

(2)

式中：A0为探测信号的幅度；ω0为探测信号的中心频率；jc(t)为调制信号的函数；t为时间；m为调制指数;g(t)为调制函数。

在单频方案的被动型星载氢钟应用中，调制信号函数jc(t)一般为正弦波；在双频方案中，jc(t)为按照一定周期跳动的4个常数，两两一组分别用以探测微波腔以及原子信号，如图2的工作模式。

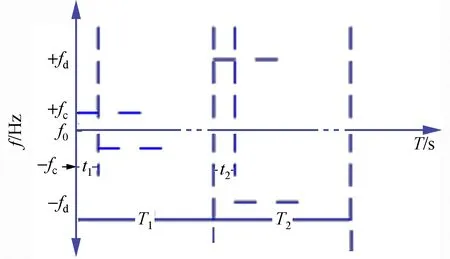
图2 探测信号工作时序Fig.2 Detection signal time sequence

2.2 误差信号的特性分析

如上所述，微波腔及晶振两路的探测信号以f0为中心频点，在各自时间周期内经过物理系统后，携带着相应的误差信号输出至电路系统。如图1所示，经过下变频组件将频谱搬移至中心频点为 19.6 MHz 的中频信号。

在探测信号初始馈入物理微波腔时，中心频率偏差较大，无法激励出微波腔误差信号及晶振误差信号，误差自测信号显示为噪声。当微波腔温度稳定后，变容二极管控制电压以及晶振压控电压进入可控范围后，被动型星载氢原子钟探测出来的输出信号均为各自带有幅度信息的调制信号，误差信号示意如图3所示。

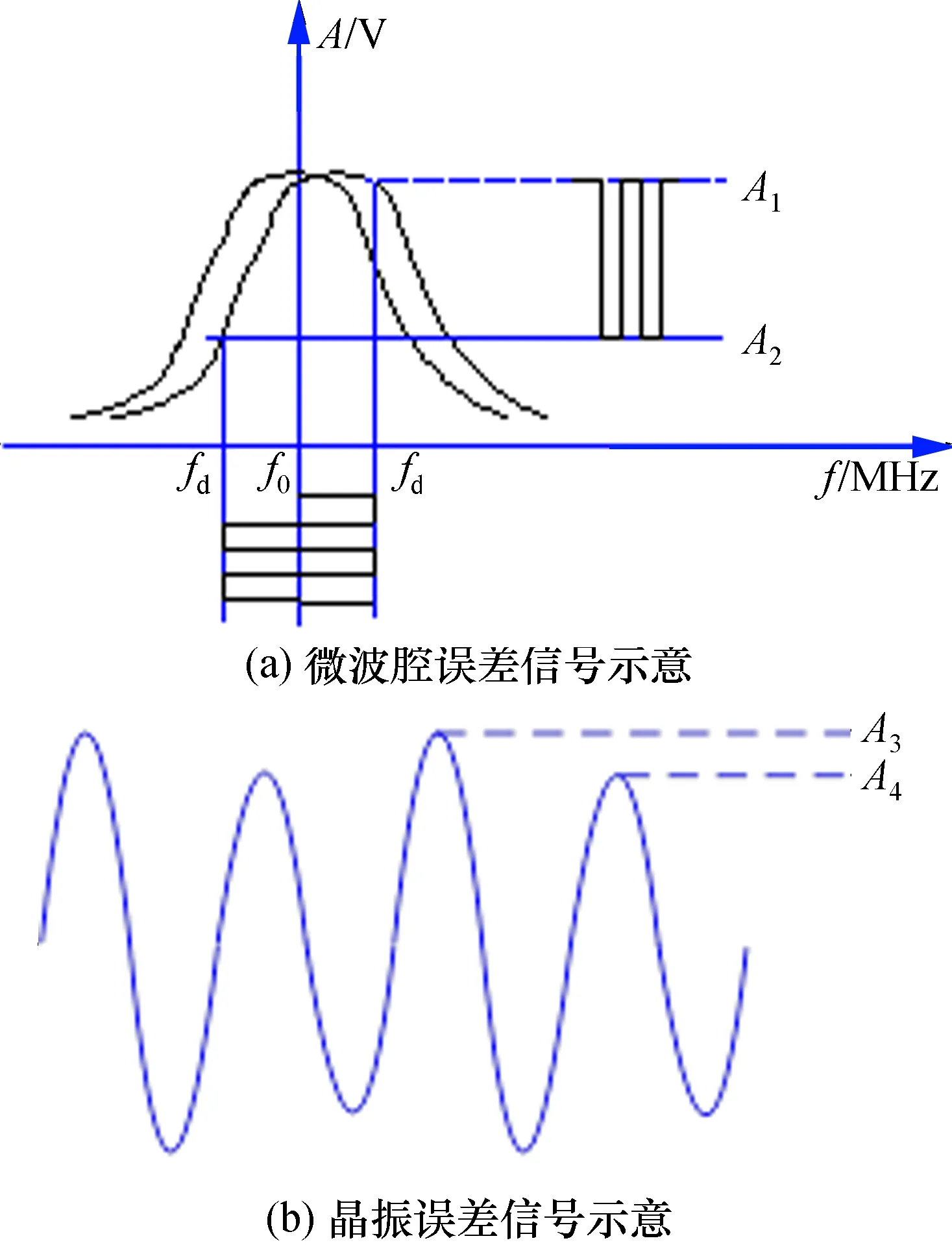
图3 误差信号示意图Fig.3 Schematic diagram of error signals

3 方案实现

3.1 误差信号包络检波方案的实现

包含有两种误差信号的调幅波，载波信号经过下变频组件后频谱被搬至19.6 MHz，再通过信号放大、积分滤波、包络检波、信号分离以及电平变换的方法从而实现误差信号的分离、提取。信号流程如图4所示。

在物理系统分别激励出的T1和T2周期的晶振误差信号和微波腔误差信号由于相应的探测信号功率相差11 dB，因此解调出的误差信号功率也相差较大，故需要找到一个合适的包络检波二极管入口功率。方案中前级的中频放大器以及阻抗匹配电路实现了电平的可调整性以及阻抗的50 Ω匹配，避免了因放大链路自激从而导致检波二极管功率堵塞顶饱和。图1中的下变频组件与中频放大器链路总增益共约75 dB，如阻抗匹配失配或中频放大器在工程设计中接地效果不佳，则极易发生信号自激。

在二极管包络检波将图3的误差信息从调幅波以包络的形式检出后，直流电平较低，信号中可能混有串扰的载波信号以及复杂多变的系统噪声，对误差信号的采样计算精度会有一定程度的影响，该影响足以恶化被动型氢原子钟输出基准信号的性能。故后级通过窄带低通滤波器进行滤波平滑。通过其S(2,1)参数仿真结果如图5可知，方案中采用的滤波电路在载波频点处约有45 dB的抑制能力，足以防止干扰信号对误差信号检波电平产生影响。

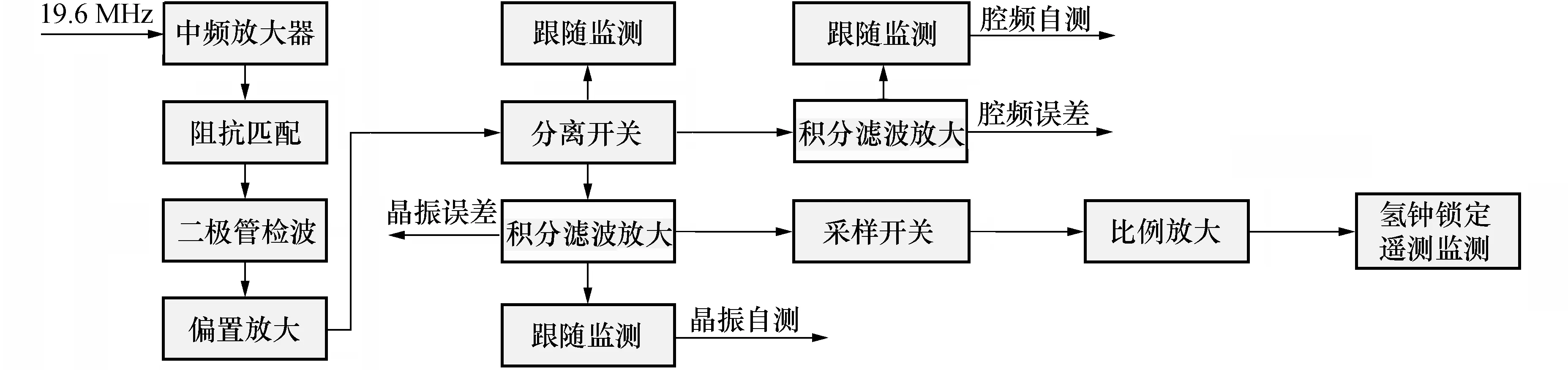
图4 误差信号提取分离框图Fig.4 Block diagram of error signal’s extraction and separation

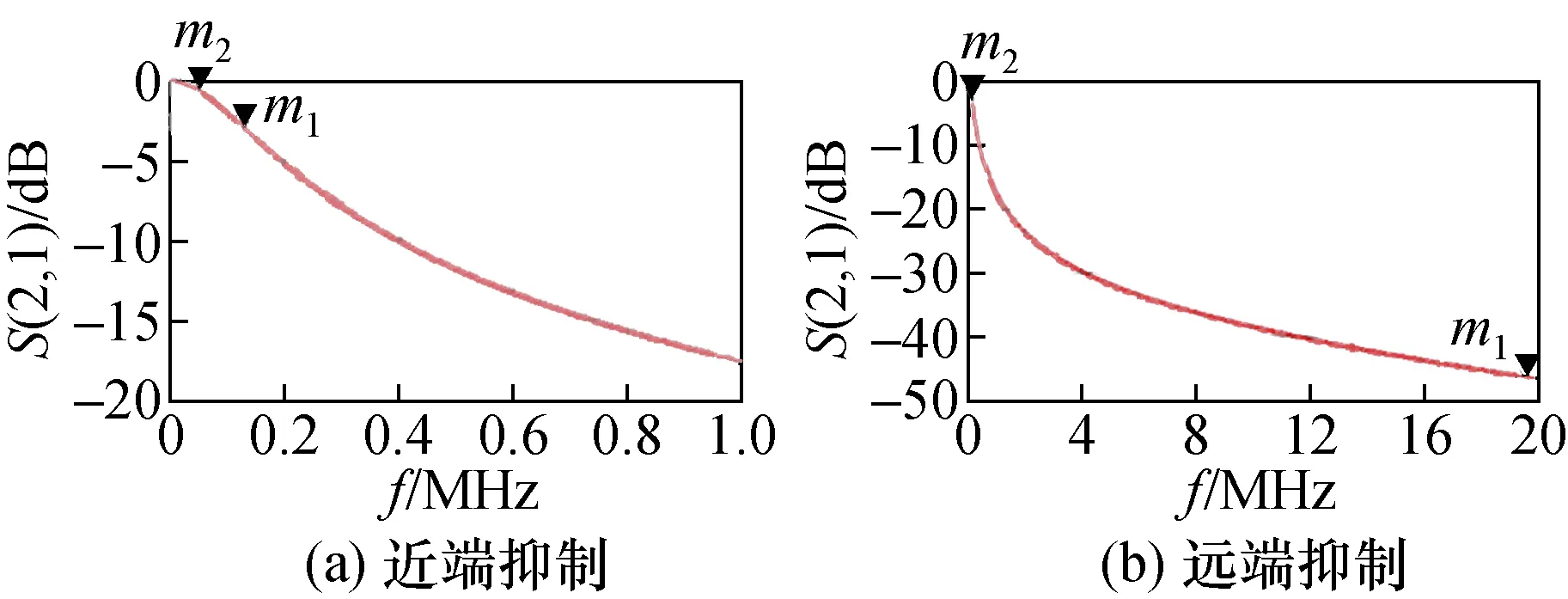
图5 滤波特性Fig.5 Characteristics of filter

根据前文分析可知，因在T1和T2周期内的探测信号的功率特性不一样，故包络检波出的包络电平也是有区别的。在T1周期内的晶振误差信号较弱，在T2周期内的微波腔误差信号较强，故在实现误差分离前，需对解调出来的误差信号进行电平运算，以满足后级的采样精度要求。因为物理系统的原子跃迁信号增益是有差异的，信号的信噪比同样也有所区别，故包络检波的通道设计的原则是让两路误差信号尽量清晰，并处在通道的线性区，不允许有失真情况存在。因此，设计了检波滤波后的第一级运算放大电路如图6所示。因采取的是调幅信号负包络检波，故对解调出的包络电平进行反向放大。同时为了防止外部参考偏置电压的抖动或者噪声对信号的提取有影响，图6中+6 V外部参考偏置电压源采用高精度稳压二极管独立电路，有效地防止了上述可能的负面影响。

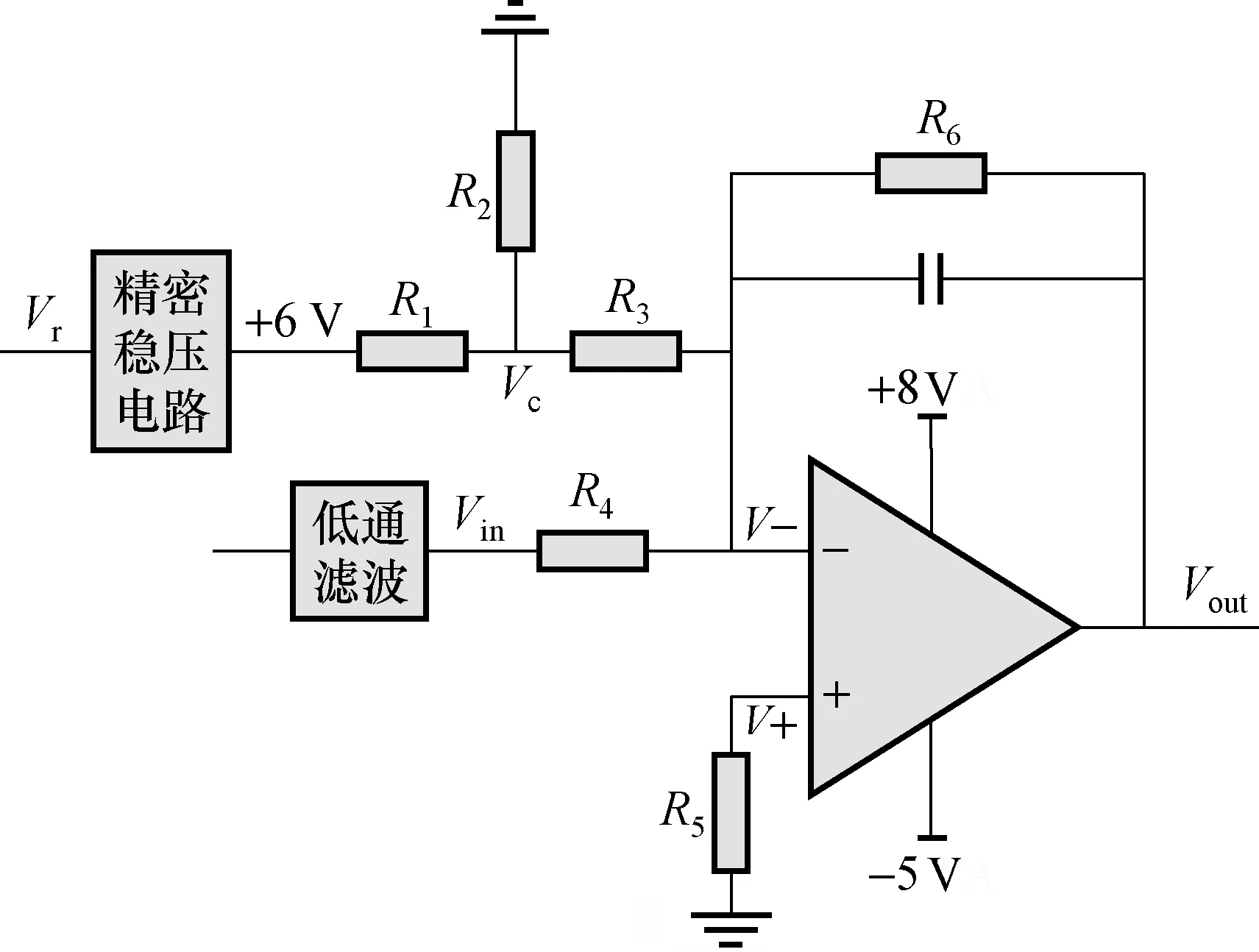
图6 检波后电平转换电路Fig.6 Convertor circuit

图6中，检波电平偏置及放大输出计算等式如下：

令

(3)

(4)

式中：Vc为外部参考偏置电平;Vout为误差信号经过运放放大后的电平。则

(5)

分析式(4)得知，电路中的电阻R4决定了包络检波出的误差信号的放大倍数，而Vc决定了误差信号的直流偏置电平位置。根据不同的原子钟的误差信号特性，需要将误差信号尽量放大清晰并处在合适的偏置电平位置。

3.2 误差信号的分离提取

在完成了误差信号包络检波及电平变换后，要考虑如何将T1和T2时间范围内的两路误差信号分离出来分别做处理。本研究采用的是三路二选一的模拟开关CC4053来实现分离方案。原理如图7所示。

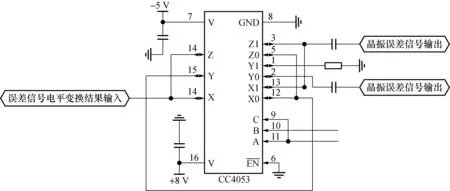
图7 误差信号分离开关原理图Fig.7 Principle diagram of error signal separation switch

两路经过电平变换后的误差信号通过第一路X(和Z通道并联使用)通道后，通过开关控制信号S1将T1时间内的晶振误差信号从X1通路经过隔直电容后取出，波形如图3(b)所示；T2时间内的腔频误差信号送入Y通道，并通过开关控制信号S2提取出T2周期时间内的误差信息同样经过隔直电容后取出，波形如图3(b)所示,进而实现了两路误差信号的分离。误差信号分离控制时序需和探测信号频点跳变时序一致，才能尽可能多的有效采集到误差信号。

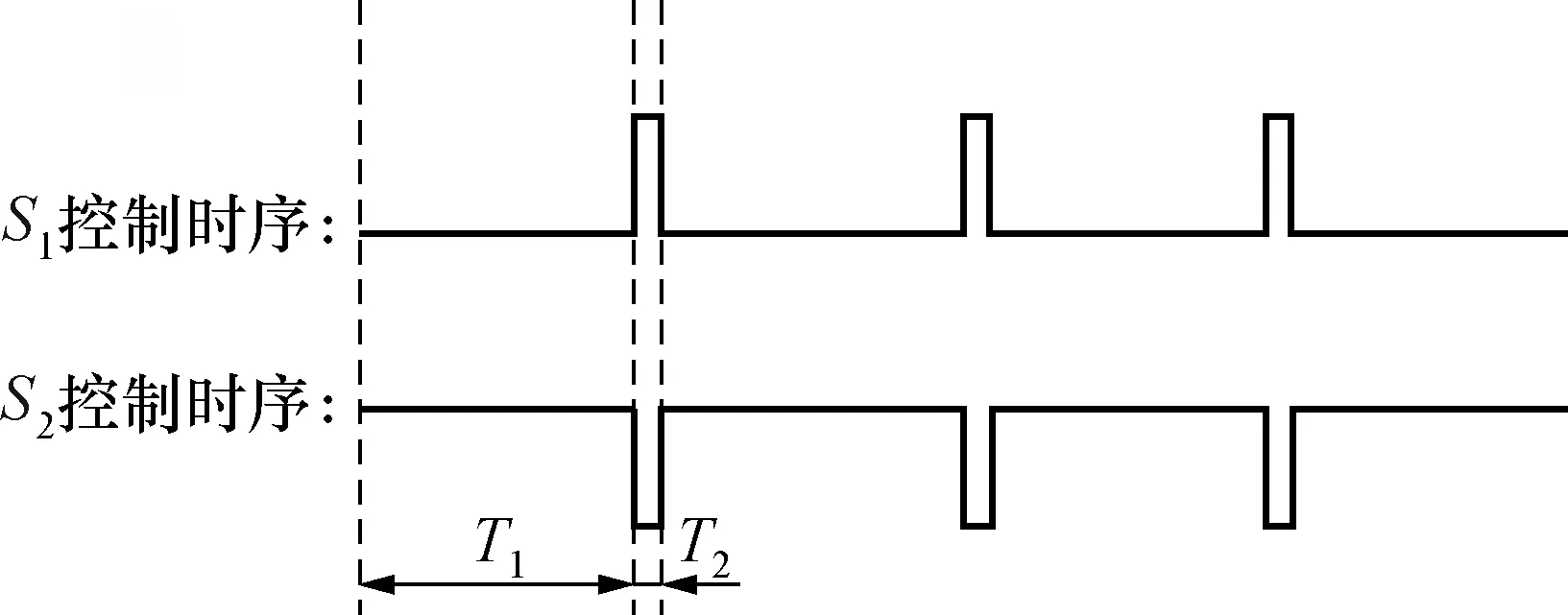
图8 误差信号分离控制时序Fig.8 Error signal separation control sequence

3.3 遥测信号的实现

被动型星载氢原子钟锁定后的稳定状态应是恒温晶振锁定在了氢原子的跃迁频率上，该锁定环路消除了上述的两路误差之一的晶振误差，即图3(b)中的A3及A4幅度值无限接近相等。在第1.4节中实现误差分离后，根据两路误差信号的特性，再次分别进行滤波放大。原子跃迁信号被锁定后，由于幅度误差被消除，物理系统输出稳定的类似正弦波信号。同样采用CC4053开关，先通过X通道取出了误差信号的正半周信号，其次对该正半周信号的峰值进行了采样保持，平滑滤波后作为遥测电压输出。该信号的遥测值除了反映星载氢原子钟是否锁定外，一定程度上反映了激荡出的氢原子跃迁出的信号的质量，是在轨时对星载氢原子钟性能判断的主要手段。

图9 锁定遥测生成原理图Fig.9 Diagram of locking telemetry’s generation

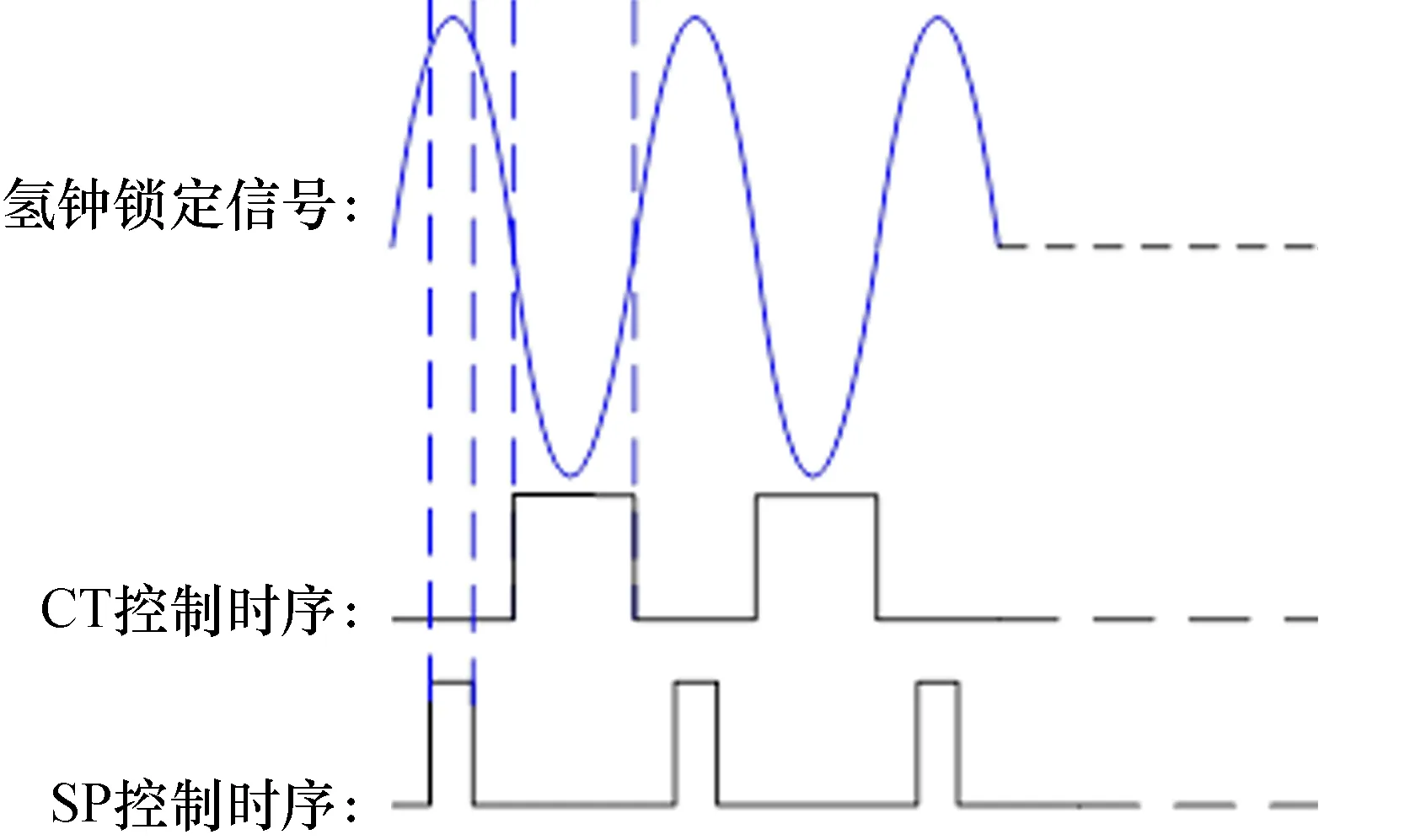
图10 遥测电压采样时序Fig.10 Telemetry voltage sampling sequence

4 结果分析

根据对被动型星载氢原子钟物理部分输出的调幅信号功率及下变频组件链路增益计算后可知，中频放大器入口调制电平总范围约为-10～-32 dBm。通过输入纯载波信号(幅度不变，检波后为固定电平)，设步进为1 dBm，测出包络检波解调通道中第一级运算放大器输出电平的标校情况如表1所示，均在通道的线性区内。

现模拟物理部分输出信号，通过信号模拟器生成载波19.6 MHz的AM调幅信号，调制信号25 Hz，调制深度设为40%，输入调制信号波形如图11所示。

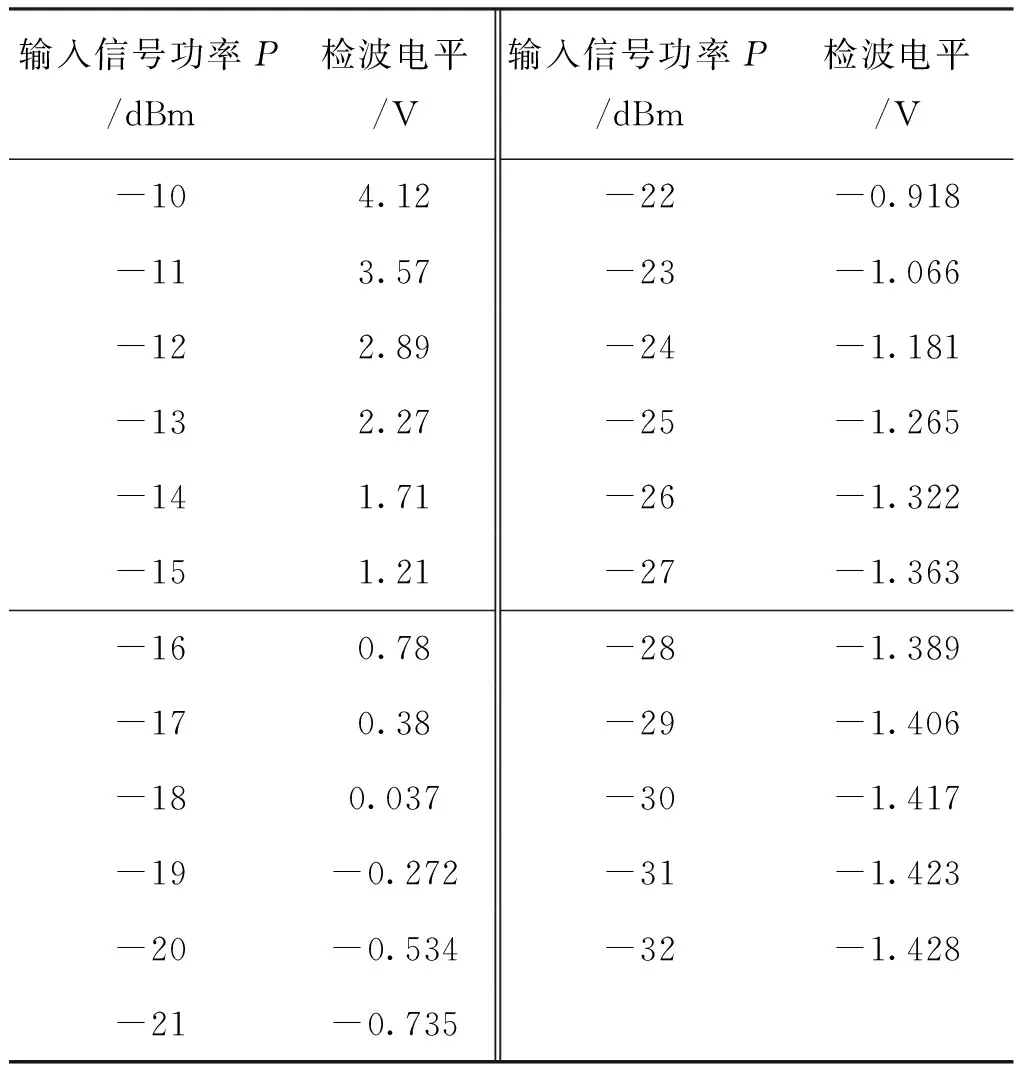
表1 检波电平标校Tab.1 Voltage of detector

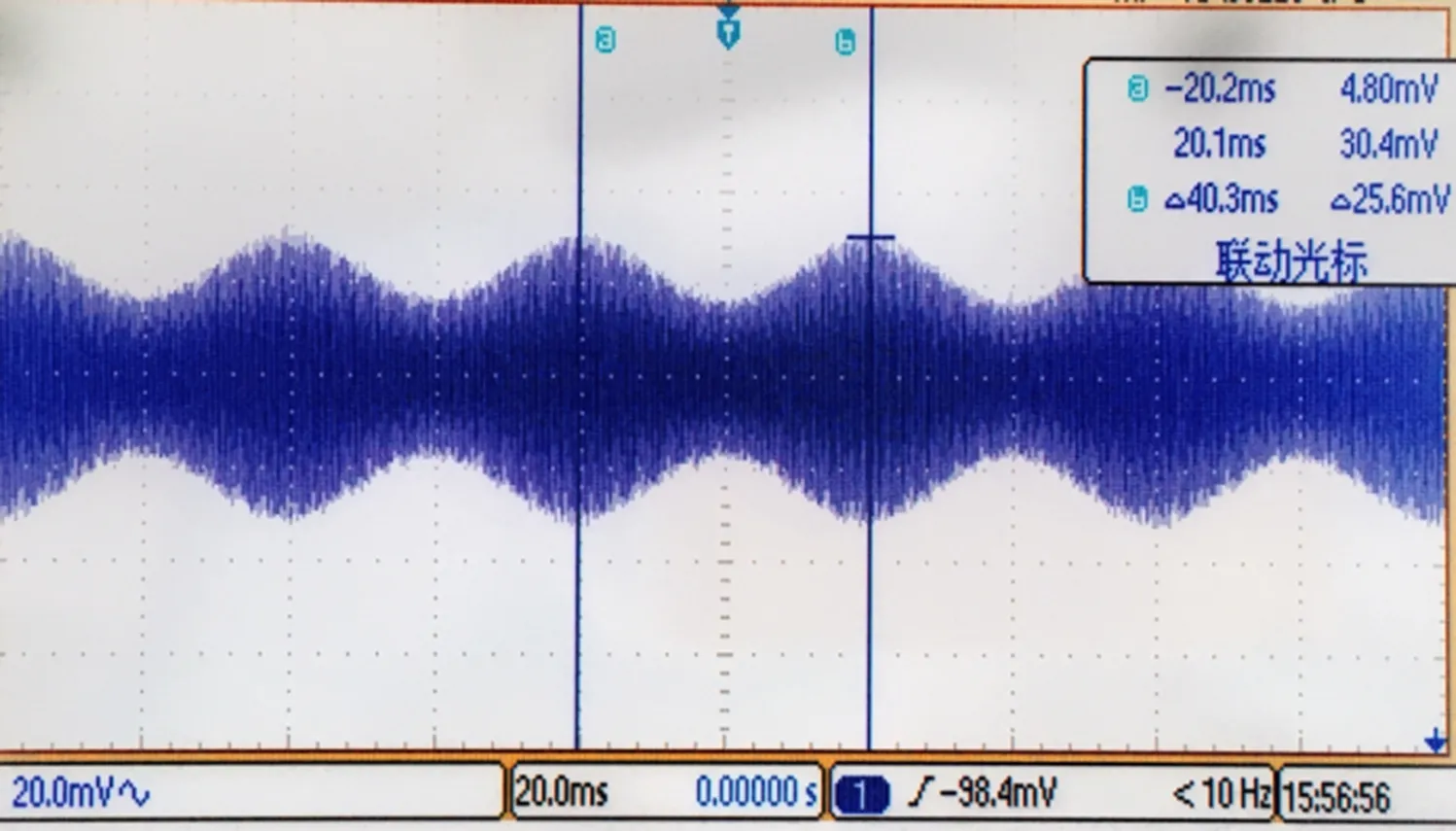
图11 调制信号输入波形Fig.11 Waveform of modulated signal

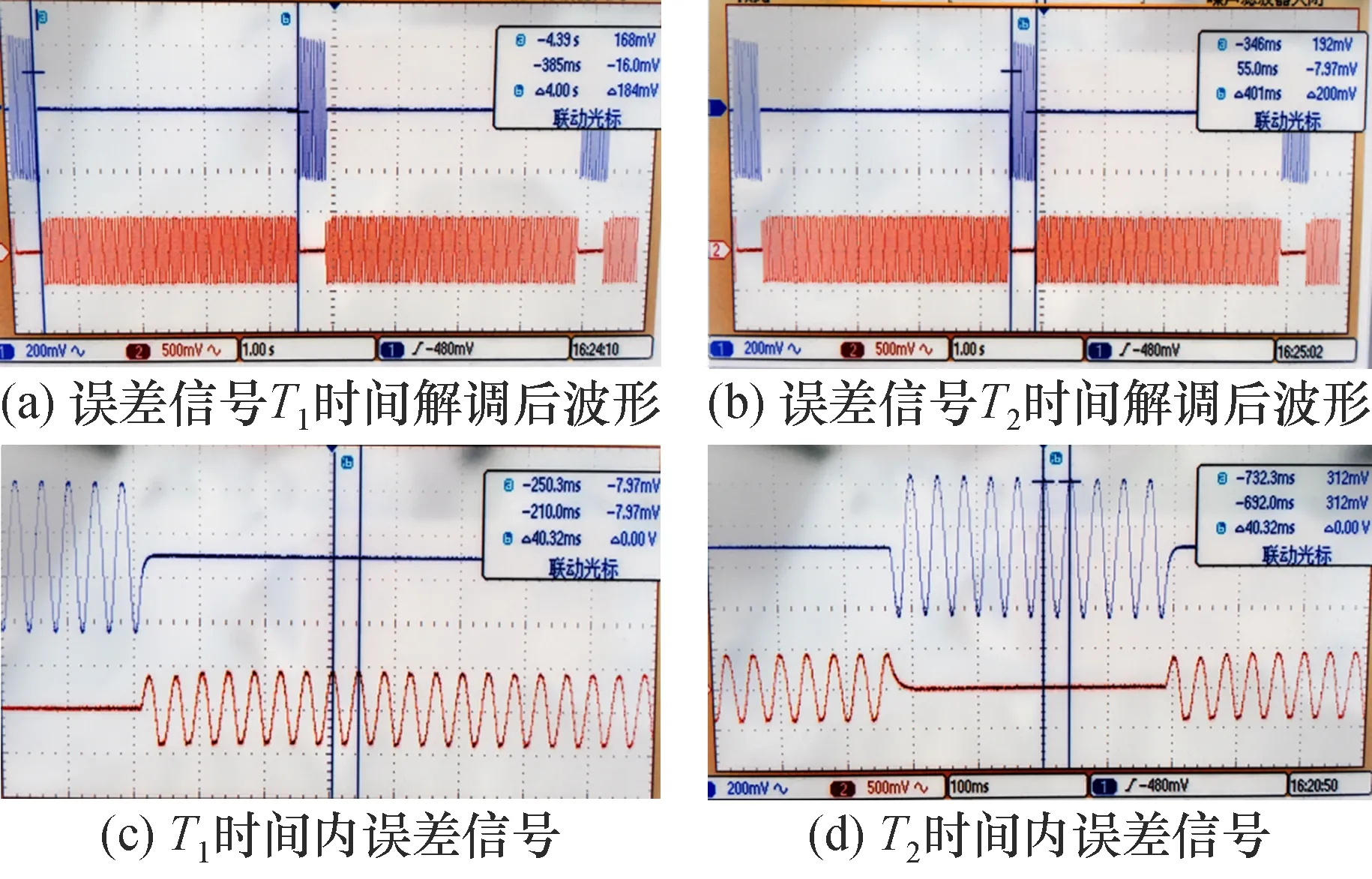
图12 解调后误差信号波形Fig.12 Error signal waveform after demodulation

5 结 论

本文研究了被动型星载氢原子钟双频方案的幅度调制误差信号通过包络检波的实现方法，分析了如何将氢原子钟两路误差信号分离提取。通过相关通道的理论分析以及验证测试表明，本方法能够实现被动型星载氢钟两路误差调幅信号的精确解析，后续研究将考虑误差调幅信号数字解调的方案，其优点是硬件资源使用较少，控制时序配置更加灵活，且更加有利于实现后续的原子钟小型化设计。