100 kA快响应精密冲击分流器研制及特性分析

龙兆芝， 李文婷， 范佳威， 谢施君， 刘少波， 余也凤

(1.中国电力科学研究有限公司，湖北武汉430074；2.国网四川省电力公司电力科学研究院，四川成都610072)

1 引 言

雷击至输电线路、建筑等物体上时产生极高的电压，导致绝缘闪络或击穿的同时，还附带强大的冲击电流，这将产生非常高的地电位抬升，严重危害设备和人身安全[1～4]。许多电气设备的设计中都要考虑暂态电流耐受能力；防雷设备、避雷装置都需要进行冲击电流耐受试验。因此，冲击电流测量的准确性直接影响防雷设备、接地网的防雷性能评价[5，6]。由于冲击电流为暂态电流信号，具有短时性和不可复现性，且其波形种类很多，时间参数跨度很大，因此相较于直流电流和工频电流，测量结果的不确定度分量更多，量值溯源的难度更大[7]。目前国际上各国计量研究院公布的测量能力中，仅德国联邦物理技术研究院(PTB)建立了20 kA、(8/20)μs的冲击电流标准测量系统，刻度因数测量不确定度为5×10-3(k=2)，时间参数测量不确定度为2×10-2(k=2)。

冲击电流测量系统包括电流转换装置和二次采集装置。电流转换装置主要分为基于电磁感应原理的罗氏线圈、磁场传感器以及基于电阻原理的分流器[8～10]。罗氏线圈和磁场传感器适用于防雷产品的雷电流耐受试验，优点为不直接接入回路，接线较为简单，缺点为阶跃响应慢，一般为200 ns左右；由于积分回路为电子回路，比例系数受温度影响较大[11～13]。分流器为具有极低电感的电阻，阶跃响应快，分流器的阻值为金属体电阻，稳定性好[14～17]，因此，更加适合作为标准电流转换装置。目前，我国尚未建立冲击电流标准测量装置，随着测量技术不断发展，测量手段不断完善，溯源方法也进一步完善。本文介绍一台100 kA精密冲击分流器的研制及其特性参数理论分析和试验验证，研究冲击电流测量装置的溯源方案和不确定度评定方案。

2 冲击电流测量

2.1 电流波形分析

根据国家标准GB/T 16927.4对雷电流波形的规定[18]，目前模拟雷电流的冲击电流分为指数型电流波形与方波电流波形。绝大部分电气设备的耐受电流试验主要采用指数型冲击电流波形，如图1所示，其主要特征参数为电流峰值Ip、波头时间T1和半峰值时间T2。图中T为电流峰值0.1倍处点与电流峰值0.9倍之间的时间间隔，波头时间T1=1.25T，半峰值时间为视在原点与波形下降沿50%峰值处的时间间隔T2，因此不同时间参数的双指数冲击电流波形可表示为：T1/T2，其中4/10 μs、8/20 μs的雷电波电流波形属于最常用于雷电冲击电流测试的电流波形。根据防雷设备的耐受电流峰值范围以及我国各单位配置的冲击电流测量装置的额定电流，研制冲击分流器设计参数为：额定电流为100 kA，测量波形为4/10 μs、8/20 μs的双指数雷电流波形。对波形进行频谱分析，雷电流99.5%以上的频率成分小于200 kHz，因此测量装置的响应时间满足200 ns以内，可保证电流波形的测量。使用分流器作为电流装换装置时，可保证其响应特性满足该要求。

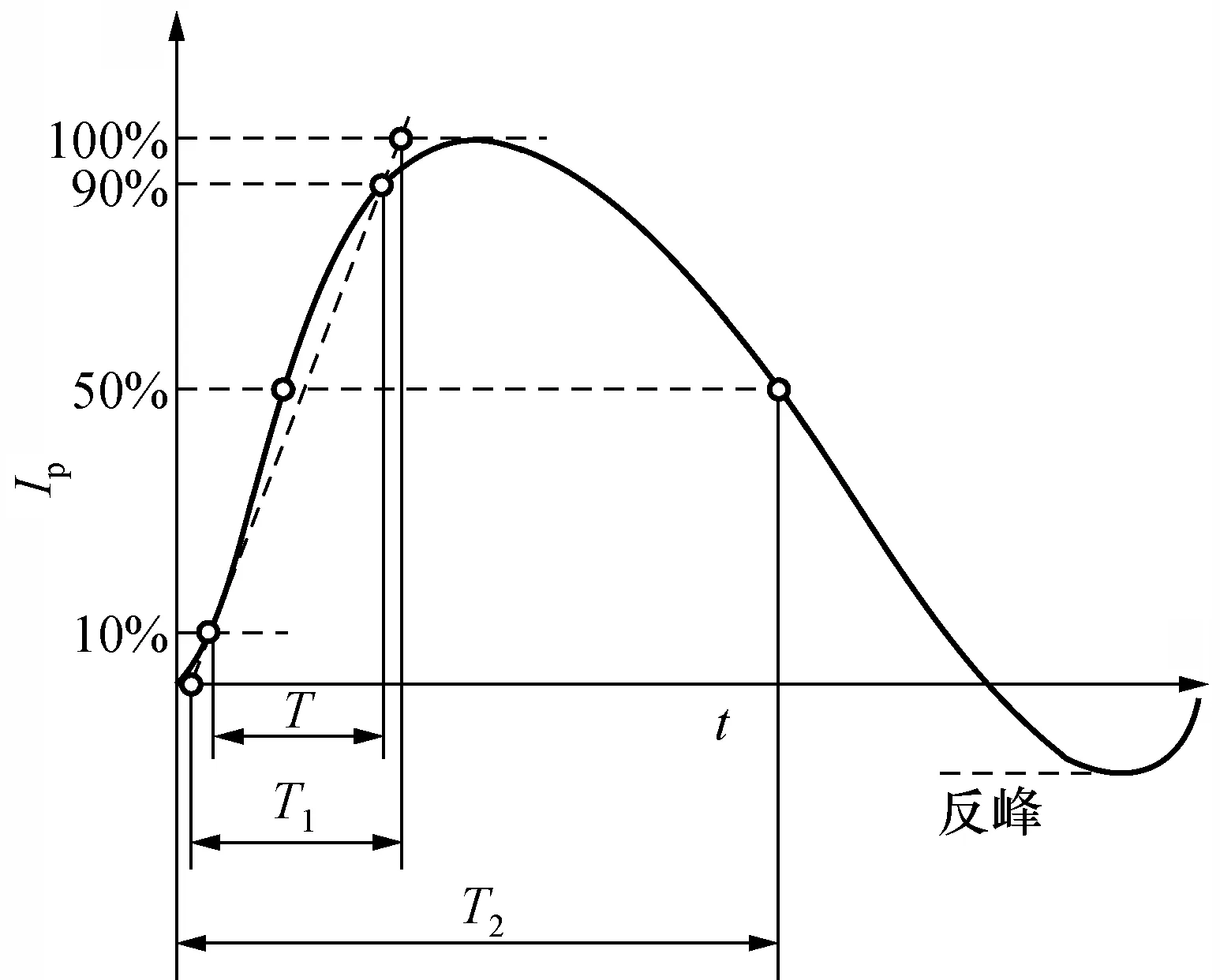
图1 标准雷电波示意图Fig.1 Standard lightning waveform

2.2 分流器原理

分流器按其结构可分为双股对折式分流器、同轴管式分流器和盘式分流器等。对折式分流器的残余电感较大，阶跃响应性能较差；盘式分流器阶跃特性好，但可测量的电流幅值较小[19]。而同轴分流器兼顾杂散电感小，响应特性好；电阻值较大，电阻体温升小的优点，因此同轴式分流器是最适合作为标准冲击电流转换装置的分流器结构，其结构如图2所示，其中：1是电流输出铜杆，2是隔离绝缘片，3是电阻体，4是铜外壳，5是测量电压导线，6是输出电缆接头。

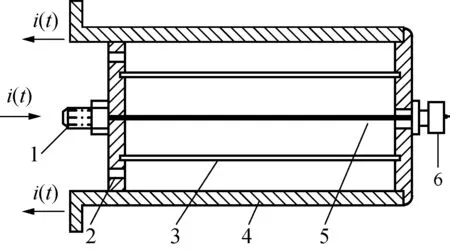
图2 分流器的结构Fig.2 Schematic diagram of impulse shunt

分流器的电阻体一般使用金属箔卷焊成圆筒形状，其电阻值的计算公式见式(1)[19，20]，本文设计的分流器电阻值的设计值为1 mΩ。

(1)

式中：R0是电阻值，Ω；ρ是材料电阻率，Ω·m；l是电阻长度，m；a是内径，m；h是电阻厚度，m。

根据同轴分流器的结构，杂散电感根据式(2)进行计算：

(2)

式中：L0是电感值，H；h是电阻厚度，m；r是电阻体内径，m。

大电流流经金属导体时，电流分流将趋近于导体外侧，且电流频率越高，趋肤效应就越明显，因此为了改善电阻体的频率特性，需要计算电阻体的渗透深度δ[21]：

(3)

式中：δ是渗透深度，m； μ0是真空磁导率，4 π×10-7H/m； μr是相对磁导率； f是被测电流频率，Hz。

导体层厚度必须小于δ/2。假设电流频率为200 kHz，金属体电阻率为0.5×10-6Ω·m，计算结果渗透深度为0.712 mm，因此实际导体层厚度应小于0.35 mm。为进一步减小趋肤效应的影响，实际选用的金属导体厚度小于0.1 mm。

2.3 温升计算

当脉冲大电流流过分流器时，由于其持续时间短，来不及散热，可认为脉冲大电流产生的全部热量都被电阻材料吸收。电阻材料吸热后，温度升高。温度太高会在电阻材料中引起较大的热应力甚至使电阻圆筒和绝缘介质烧坏。一般允许温升小于100 ℃[22]。温升与电阻变化的计算公式见式(4)、式(5)：

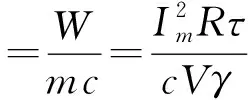
(4)

ΔR=ΔϑRα

(5)

式中：Δϑ是温升，K；W是分流器中消耗的能量，J；m是电阻材料的质量，kg；c是电阻材料的比热容，J/(kg·K)；R是分流器的电阻，Ω；ΔR是分流器电阻的变化量，Ω；α是温度系数，K-1；γ是密度， g/cm3；τ是时间间隔，s。

3 分流器研制

3.1 电阻温度系数

使用恒温箱测量电阻材料在(-1～90)℃范围内的温度系数。将电阻材料放置在恒温箱中，使用阻抗分析仪WK6500B测量电阻值，室温(20±2)℃，为了减小电阻引线引入的测量误差，采用四线测量法测量电阻。图2(a)为实验接线回路，图2(b)为测量结果，以-10 ℃的测量结果作为起始点，从图中可以看出康铜的温度系数约为-4×10-5/K，锰铜材料的温度系数为5.5×10-5/K。因此选用康铜材料作为分流器电阻的材料。另外试验过程中发现，一旦温度发生剧烈变化(突升或突降)，电阻值将随之产生较大改变，因此在实际使用分流器时应尽量避免外界环境温度的突变。

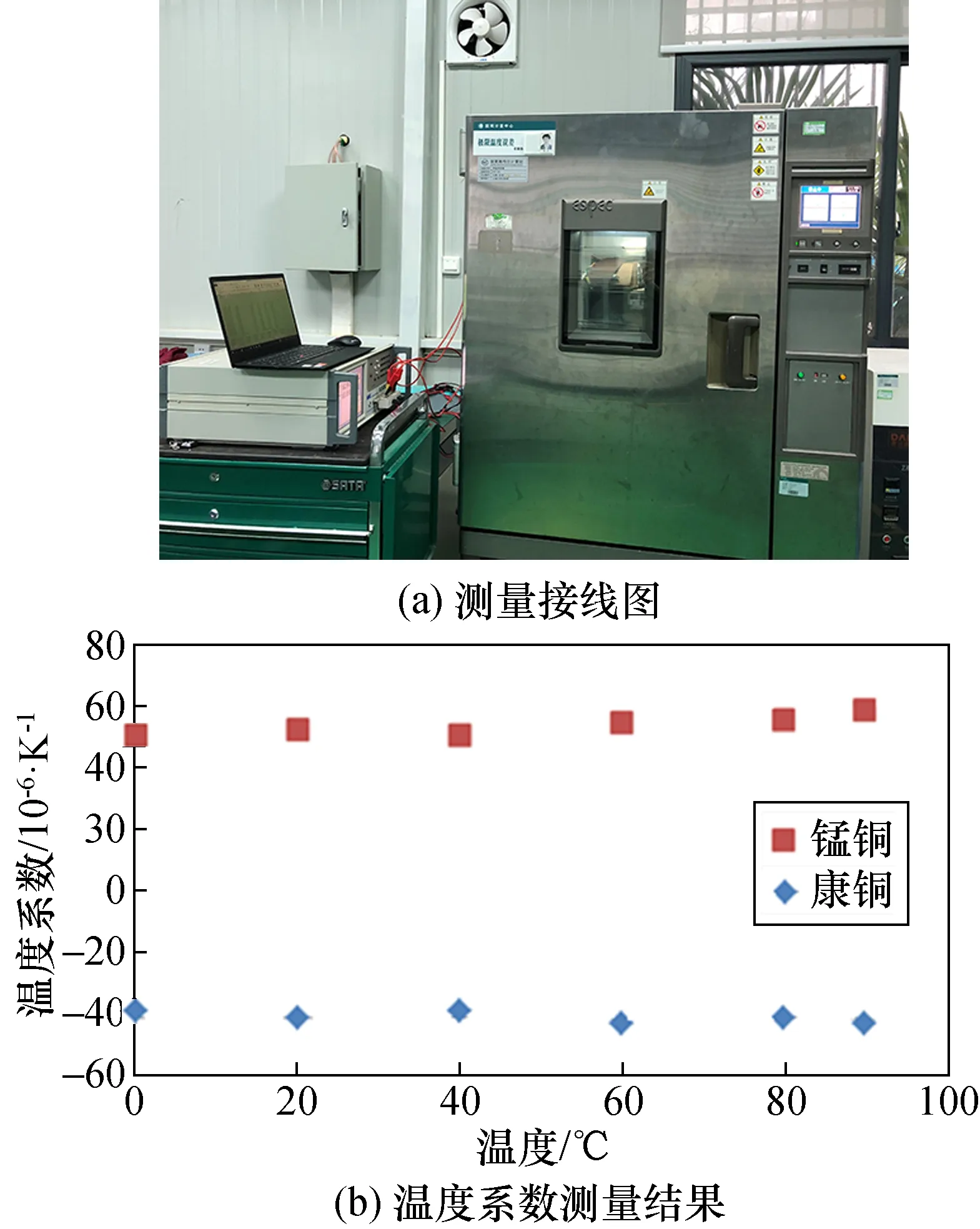
图3 电阻材料温度系数测量Fig.3 Measurement of temperature coefficient of resistance materials

使用0.1 mm康铜箔研制如图2所示100 kA同轴管式分流器，电阻箔在聚四氟乙烯支撑筒上卷绕成圆筒状，电阻体首尾焊接在黄铜杆上，回流金属外壳也采用黄铜加工。

3.2 动态特性

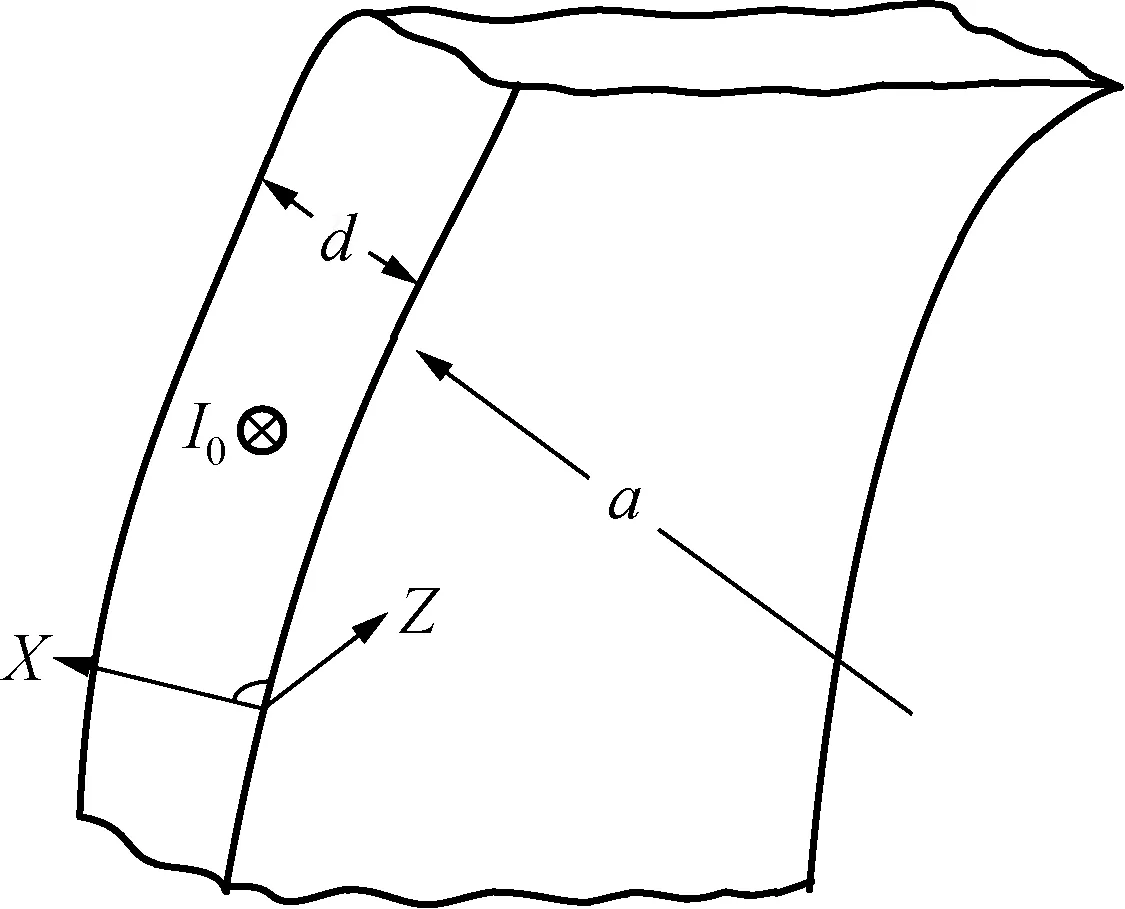
图4 电阻体截面示意图Fig.4 Cross section diagram of resistance

当一个理想阶跃电流I0流入同轴管式分流器时，初始时刻电流在导体表面无限薄层中流动。在同一瞬间，导体外会产生磁场，如图4所示。当电流分布在电阻体的整个横截面上时，外部磁场穿透导体内部。根据麦克斯韦方程计算磁场H0在导体中随时间变化的传播，由于d≪a：

(6)

(7)

式中：t是时间，s；x是径向穿透厚度，m；a是电阻体内径，m；b是电阻体外径，m；d是电阻厚度，m。

利用感应定律，计算出的通过内表面近轴线的电压降为：

(8)

式中：eM(t)是电压降，V；I0是电流，A；R0是电阻值，Ω；t是时间，s；L0是电感值，H；υ是传播速度，m/s。

这些方程描述了同轴管式分流器的阶跃响应。管式分流器上述方程对应于图5(a)所示的等效电路，将分流器等效成n段，n个电阻元件R0的并联为分流器的直流电阻值R，n个电感串联为分流器的内部杂散电感。管式分流器在电流阶跃上升沿时刻也没有感应峰值，t=0时，式(10)中，I0R0右边部分为0，此时电压降为0。图5(a)可简化成图5(b)，图中L′的计算公式为：

L′=0.43L0

(9)

式中：L′是电阻体等效电感值，H。

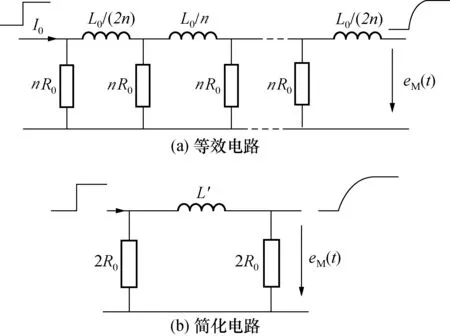
图5 分流器等效电路Fig.5 Equivalent circuit of shunt

计算上升时间为：

T1=0.167L0/R0=0.167μd2/ρ

(10)

测量带宽为：

B=1.46R0/L0=1.46ρ/(μd2)

(11)

3.3 改善输出电压波形

图6为分流器输出信号测量导线的连接方式，测量瞬态电流时，由于趋肤效应的影响，电流分布在最外层，因此将输出导线焊接在导体外侧可改善其测量特性，将绝缘支撑杆和导体钻孔用于导线穿入。分流器流过的电流不会在绝缘筒内部产生干扰磁场，因此输出电压不包含任何感应干扰分量。

图6 分流器输出电压信号连接方式Fig.6 Connection method of output voltage signal of shunt

表1为分流器技术参数表，分流器电阻的内径为150 mm，厚度为0.1 mm，长度为95 mm，电阻值为0.967 5 mΩ。假设冲击电流峰值为100 kA，脉宽为50 μs，计算得到分流器电阻的温升为36.3 ℃。

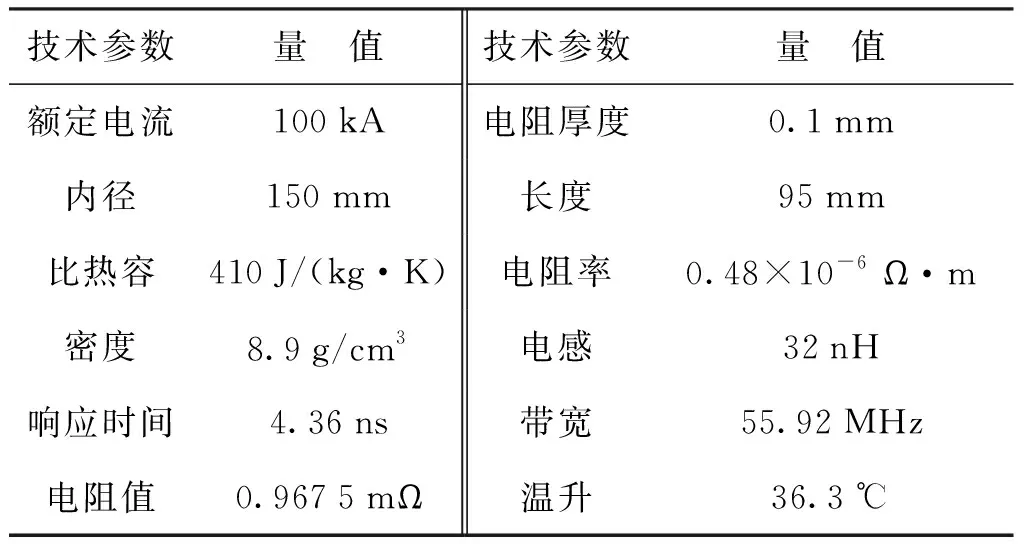
表1 100 kA分流器技术参数Tab.1 Technical parameters of shunt with rated current 100 kA

4 特性试验

4.1 稳态电阻值测量

使用标准电流源Fluke5520A校准器测量所研制分流器的电阻值，校准器可产生50 Hz的交流电流，幅值(5～20)A；使用数字多用表Agilent 34401A测量分流器的输出电压。测量回路如图7所示，测量时环境温度为20 ℃，相对湿度60%。测量时分流器的输出电缆使用长度为15 m，波阻抗为50 Ω的双屏蔽射频电缆，电缆的输出端连接50 Ω的匹配电阻。校准器的内阻为kΩ级，因此输出引线的电阻对测量结果可忽略不计，测量电阻值为0.969 7 mΩ，与设计值非常吻合，根据GB/T 16927.4-2014的规定[22]，冲击电流测量装置的刻度因数为被测电流与测量仪器测量电压的比值，单位为A/V。因此该分流器的刻度因数为1031.2 A/V。

图7 稳态电阻值测量回路Fig.7 Measurement of shunt resistance under AC current

4.2 阶跃响应试验

图8(a)为阶跃响应试验回路示意图，图中：DC是直流源；R是充电电阻；C是同轴电缆；K是继电器；S是分流器；M是匹配器；O是数字示波器。从图中可以看出，装置采用同轴电缆为储能元件，使用直流源通过充电电阻对同轴电缆充电，充电完成之后，触发继电器对分流器放电，整个回路尽可能地减小回路杂散电感。分流器输出电压端连接15 m同轴电缆和匹配电阻，然后与数字示波器相连。试验时同轴电缆的长度为100 m，同轴电缆的波阻抗为50 Ω，如果电缆末端连接50 Ω负载时反射系数为0，不产生反射；但当电缆末端连接阻值为mΩ级的分流器时，相当于短路，反射系数为-1，行波完全反射，沿着同轴电缆传播。传播速度v由绝缘的介电特性和磁导率决定，计算如式(12)所示：

(12)

式中：ε为介电常数，F/m；μ为材料磁导率，N/A2；εr为相对介电常数；μr为相对磁导率；c为光速， 3×108m/s。

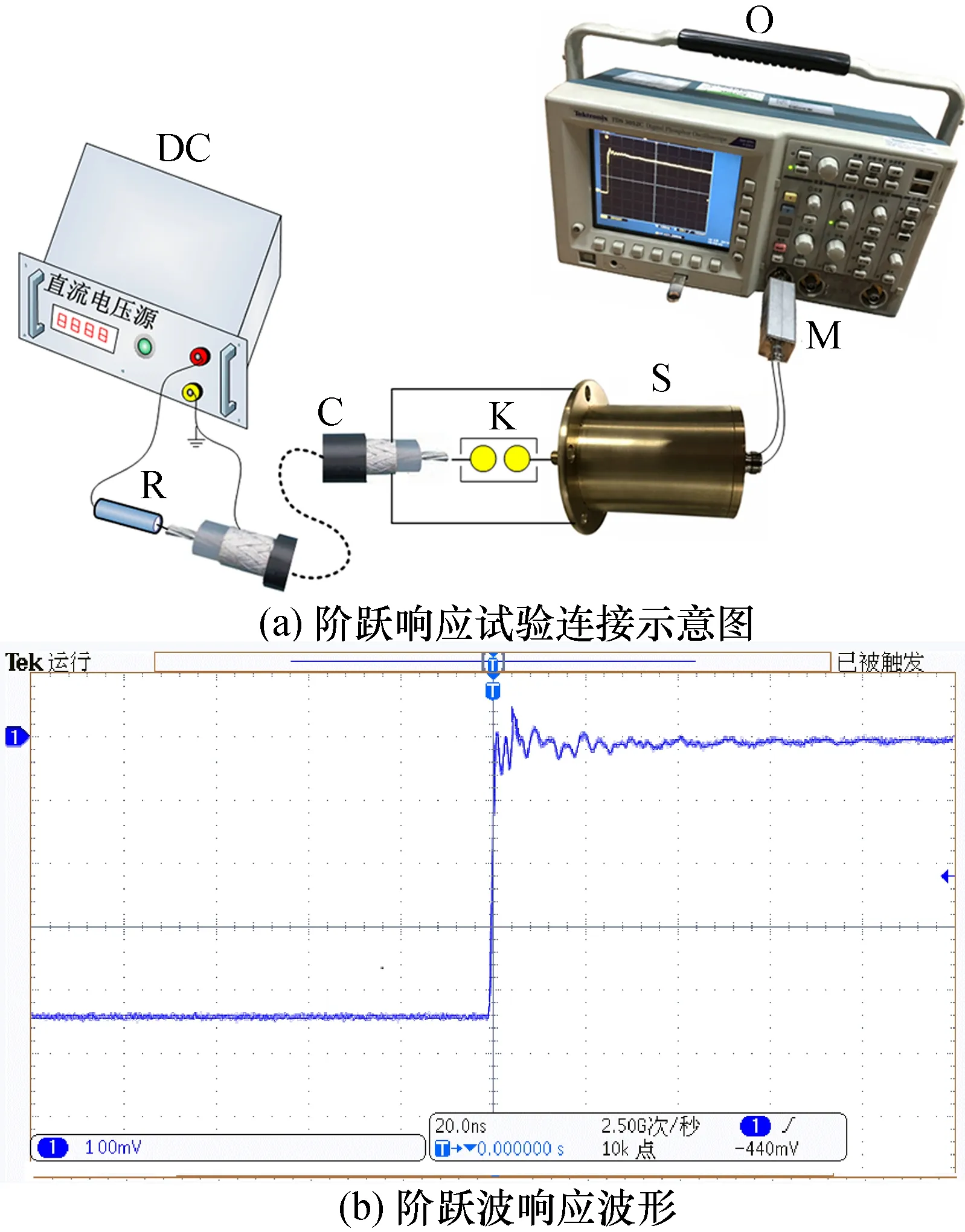
图8 阶跃响应试验Fig.8 Test of step response

同轴电缆的相对介电常数为2.3，相对磁导率为1，因此行波的传导速度为1.98×108m/s，100 m的同轴电缆从始端传输到末端需要的时间约为500 ns，回程约为500 ns，从而产生了脉宽约1 μs的方波电流信号。

图8(b)为测量得到研制分流器的阶跃响应波形，计算到分流器的上升时间为3.4 ns，过冲为13.2%，稳定时间为28 ns。因此可以看出由于不能完全消除回路杂散电感，存在过冲的同时分流器的阶跃响应时间也小于理论计算值。

分流器动态特性引起其测量冲击电流峰值和时间误差可以通过卷积积分的方法计算得到。对阶跃响应波形进行归一化处理，如式(13)所示：

(13)

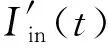
g(t)和Iin(t)以相同的采样间隔采样，并且g(t)和Iin(t)的采样点数也相同，将连续卷积转换成离散卷积的形式，如式(14)所示：

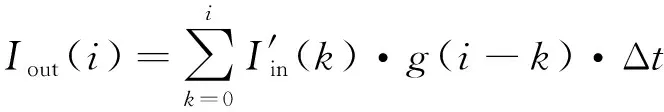
(14)

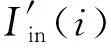
使用LABVIEW软件进行卷积计算，输入电流波形为实验室实测8/20 μs的标准雷电流波形数据，计算输出电流波形与输入电流波形的峰值误差和时间参数误差分别为0.05%，0.1%和0.08%。

4.3 测量冲击电流

由于暂态电流流入地时将抬升地电位，一个回路中如果同时接入两台分流器时，两台分流器的输出信号不能直接接入同一台测量仪器的双通道，地电位的不同将导致测量结果不准确。同时使用分流器测量冲击电流时还需要注意抗干扰措施。冲击大电流试验回路如图9所示，图中：S是分流器；Rk是匹配电阻；MC是测量电缆；H是屏蔽机箱；M是测量仪器；F是滤波器；T是隔离变压器；W是接地线。测量电缆使用双屏蔽同轴电缆，或者在屏蔽电缆外壁增加金属屏蔽层。电缆首端双层屏蔽直接接地，电缆末端外层屏蔽连接测量仪器(数字示波器、数字记录仪)外侧的屏蔽箱，测量仪器的供电电源需要通过隔离变压器或者滤波器，或者直接使用不间断电源(UPS)供电。

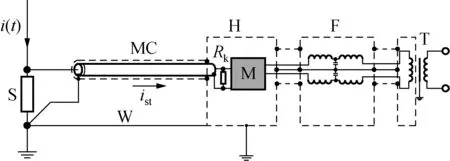
图9 冲击大电流试验回路Fig.9 Test setting of impulse high current

4.4 线性度试验

使用已校准的罗氏线圈测量分流器刻度因数和时间参数随电流峰值的变化。100 kA罗氏线圈在20 kA下测量误差为0.2%，测量不确定度为0.5%。罗氏线圈自身的线性度与已在德国PTB研究院比对的100 kA标准分流器比对得到，如图10所示，从图中可以看出，罗氏线圈的刻度因数随电流峰值的增大而减小，整个量程范围内刻度因数变化在0.5%以内，并且正负极性的变化趋势相同。

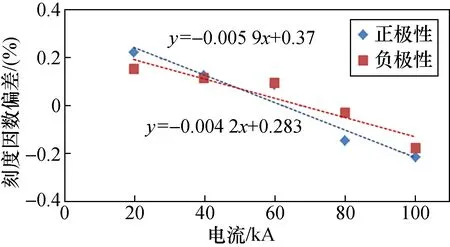
图10 罗氏线圈线性度测量结果Fig.10 The test results of linearity of Rogowski coil

图11 分流器校准回路Fig.11 Calibration circuit of shunt

使用罗氏线圈从5～95 kA电流范围内测量分流器的线性度，试验接线回路见图11。测量数据将罗氏线圈自身的线性度和时间参数误差进行修正，最终的测量结果见图12，单极性单个电流点重复测量10次。图12(a)为刻度因数随电流的变化，从图中可以看出，整个电流测量范围内，刻度因数与其平均值的相对偏差在±0.2%以内，无极性效应；时间参数测量误差也根据PTB比对的分流器进行误差补偿之后得到最终的测量结果，图12(b)为上升时间随电流峰值的变化；图12(c)为半峰值时间随电流的变化，从图中可以看出，时间参数测量误差变化非常小，测量误差在0.4%以内。

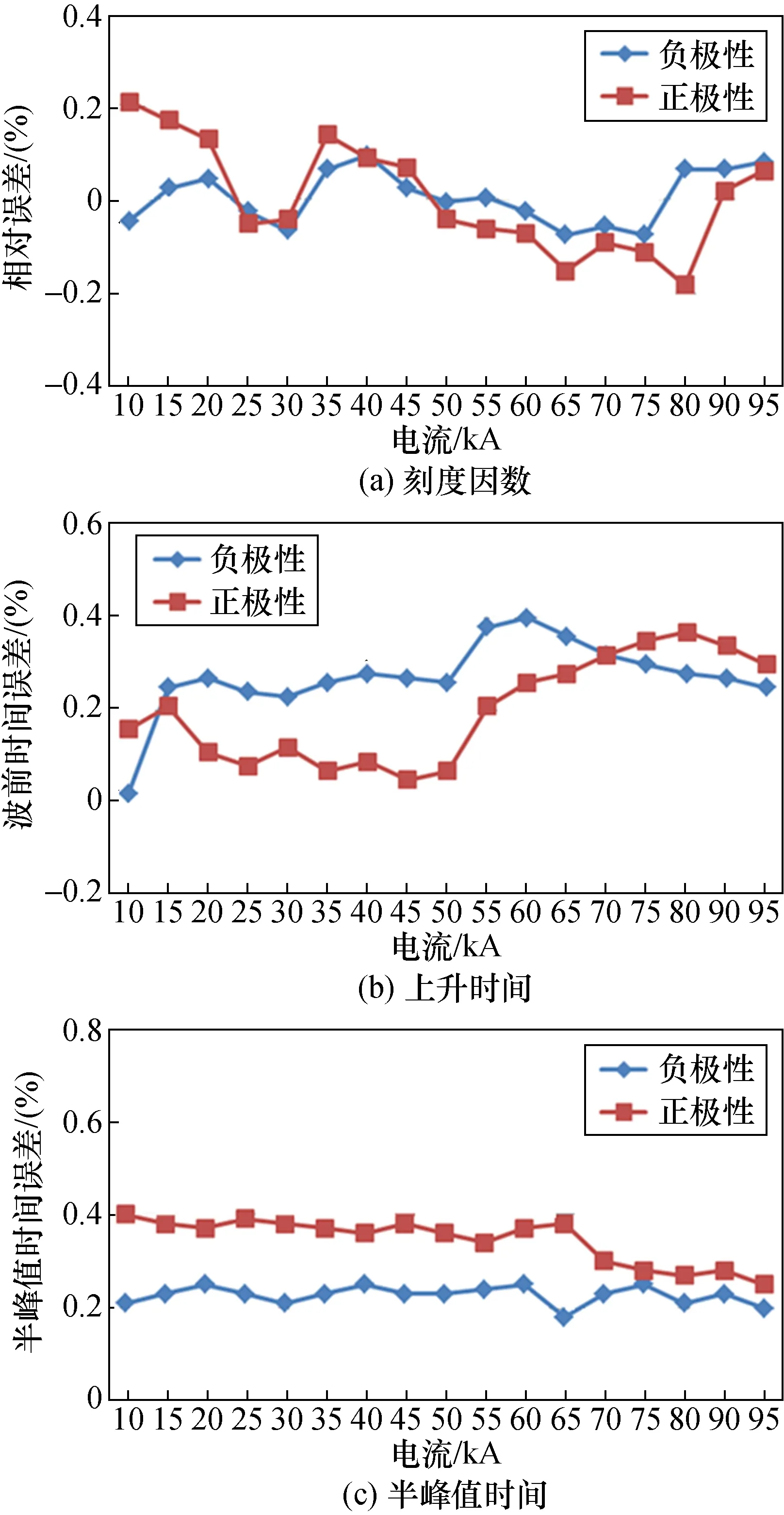
图12 刻度因数和时间参数随电流峰值的变化Fig.12 Change of scale factor and time parameter with different peak current

4.5 短时稳定性

假设短时间内在相同温度条件下，罗氏线圈的刻度因数不发生变化。在20 kA电流下校准分流器的刻度因数之后，去掉罗氏线圈，仅对分流器施加90 kA的冲击电流20次，每次测量间隔时间为 3 min， 试验结束后，再次在20 kA下使用罗氏线圈测量分流器的刻度因数，试验前后刻度因数变化0.05%。

4.6 长期稳定性

分别在2018-10-11和2019-03-12使用稳态电流源对分流器的电阻值进行5次测量，稳态电流源输出20 A的直流电流，测量不确定度为0.08%。测量方法与本文第2.3节一致，单个电流点重复测量10次，取其平均值，实验环境温度不变。不同时间点偏差最大值为0.08%。

4.7 测量不确定度评定

根据不确定度传播率的方法(GUM)[23]计算被测量估计值的测量不确定度，表2为研制的100 kA分流器与高精度数字记录仪组成测量装置后的峰值测量不确定度评定表，评定时电流转换装置和数字记录仪分开进行评定。分流器稳态刻度因数由稳态电流标准源校准得到，稳态校准源的不确定度为0.08%，正态分布。另外长期稳定性、短期稳定性、线性度、邻近回路电流影响根据试验结果计算得到，假设为均匀分布。动态特性引入的不确定度根据分流器阶跃响应波形以及被测冲击电流波形卷积法得到的测量误差计算而来，假设为均匀分布。温度效应通过分流器电阻体温度系数与温升计算得到。数字记录仪的峰值和时间参数测量误差使用冲击电压标准波源进行校准得到[24，25]，标准波源峰值参数不确定度为0.05%，其主要不确定度分量包括标准波源、线性度等。从表2中可以看出整套测量装置测量不确定度主要分量为稳态电阻值测量、线性度以及数字记录仪引入的不确定度分量，计算得到95%置信概率的扩展不确定度为0.41%(k=2)，时间参数影响因素主要为分流器的动态特性、数字记录仪时间参数测量误差以及环境条件影响，其时间参数测量不确定度0.8%(k=2)。

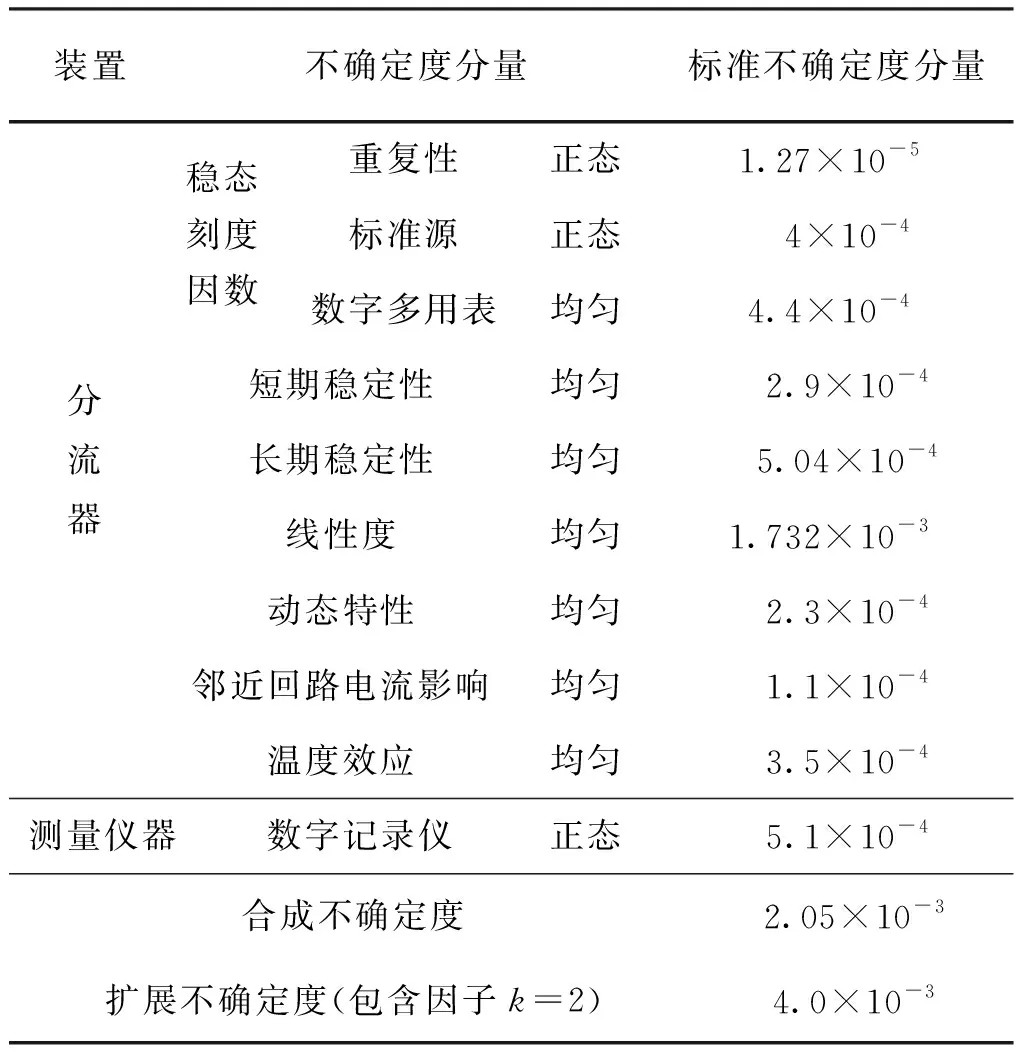
表2 测量不确定度评定表Tab.2 Evaluation form of uncertainty

5 结 论

研制了快响应精密冲击分流器，幅值100 kA，使用厚度0.1 mm的康铜作为电阻材料，其温度系数为-4×10-5/K，稳态刻度因数为1 031.2 A/V。研制的方波电流源测量分流器的阶跃响应，其上升时间为3.2 ns，使用卷积积分的方法计算分流器动态特性对所测电流波形峰值和时间参数的测量误差为0.05%、0.1%。在大电流下对分流器线性度、稳定性、邻近回路电流影响等特性参数进行测量。研究组成测量装置后的测量不确定度评定方法，测量系统中分流器和数字记录仪分开进行不确定度评定，最终评定的峰值测量不确定度为0.41%(k=2)，时间参数测量不确定度为0.8%(k=2)。说明整套测量装置可作为标准测量装置用于电流传感器的校准。