主动式双波长红外激光测温标定实验研究
曲 岩, 宦克为, 安保林, 董 伟,赵云龙, 宋旭尧, 原遵东
(1.长春理工大学,吉林长春130022; 2.中国计量科学研究院,北京100029)
1 引 言
辐射测温具有测温范围广、响应速度快、不侵入和破坏被测目标温场、理论上不存在测温上限等优点[1],近年来在我国发展十分迅速,已被广泛应用于航天、冶金和医疗等行业[2~9]。
辐射测温领域的一大难题是目标“真实温度”的获取。传统的辐射测温方法受限于目标发射率的影响,通常只能获得目标的亮度温度,无法直接测量目标的“真实温度”,尤其在发射率较低的情况下,二者之间差异巨大[10]。实际应用中,为克服目标发射率未知对辐射测温方法精度的限制,双波段比色测温方法[11]被广泛应用,一般通过分光结构获取目标在2个测量波段的能量,结合比值技术实现目标真实温度测量。尽管国内外对双波段比色测温技术进行不断地优化[12,13],如采用非调制的激光通过近似相近波段下发射率相等来消除发射率等[10],但在理论模型上都存在近似假设而无法完全消除发射率的影响。
近年来,一种新型主动式双波长红外激光测温方法逐渐受到关注[14~16],该方法通过可调制激光光源和反序光电探测结构相配合,可在待测目标表面发射率未知的条件下进行温度测量。然而,目前针对主动式双波长红外激光测温方法的研究积累较少,存在一些问题亟待解决[17]。如采用同源标定,导致测温系统适用范围狭窄;标定结果往往需要计算修正,修正量也会存在一定误差;缺乏稳定高精度的独立标定源,在外场环境下应用受限等。
因此,本文基于主动式双波长红外激光测温方法的原理,设计了一种可获取表面真实温度的高精度标定源,实验分析了标定源的稳定性和均匀性。应用所搭建的标定源对主动式双波长红外激光测温系统进行标定实验,得到了相应的标定结果。此外,对系统的可靠性进行了分析验证。
2 原 理
2.1 黑体辐射理论
根据普朗克辐射定律,辐射源的辐射能力可以通过该辐射源在一定波长λ和温度T下的辐射亮度L0(λ,T)来表征[18],表示为:
(1)
式中:c1=3.741 8×10-16W·m2为第一辐射常数;c2=1.438 8×10-2m·K为第二辐射常数;λ为波长;T为黑体辐射源热力学温度。
2.2 主动式双波长红外激光测温原理
主动式双波长红外激光测温的基本原理是双波长激光-材料相互作用下的光热效应理论,采用反序波长探测和相敏检测技术实现对未知发射率高温物体的表面真实温度进行测量。
首先,使用波长λ1的激光投射到待测高温材料表面使其产生温升ΔT,使用波长λ2的探测器来测量温升ΔT,获得的光电流Ip(λ2)可表示为:
IP(λ2)=R2·ε1·ε2·Ω2·Δλ2·τ1·τ2·
(2)
式中:R2为探测器光谱响应度函数;ε1为材料在波长λ1的光谱发射率;ε2为材料在波长λ2的光谱发射率;Ω2为测量立体角;Δλ2为测量带宽;τ1仪器系统在波长λ1的光谱透过率;τ2仪器系统在波长λ2的光谱透过率;P1为激光功率;G1(t)为与被测物体温度响应有关的系数;L0(λ2,T)为温度为T的黑体在波长λ2的光谱辐射亮度。
对于半无限大不透明物体,有
(3)
式中:K为导热系数;D为热扩散系数;ω为激光调制频率。
同样,使用波长为λ2的激光加热被测材料,用波长λ1的探测器测量,得到响应的光电流Ip(λ1)为
IP(λ1)=R1·ε1·ε2·Ω1·Δλ1·τ1·τ2·
(4)
式中:R1为探测器光谱响应度函数;Ω1为测量立体角;Δλ1为测量带宽;P2为激光功率;G2(t)为与被测物体温度响应有关的系数;L0(λ1,T)为温度为T的黑体在波长λ1的光谱辐射亮度。
将式(2)与式(4)做比,可以得到一个不含发射率项的等式:
(5)
式中:CALP为标定系数,由实验系统中的仪器参数组成,可通过实验室高精度标定源准确测定。
2.2 CALP参数标定原理
由双波长红外激光主动式测温理论模型公式(5),可以反推出标定系数CALP。需要指出的是Ip(λ1)/Ip(λ2)=S1/S2,S1/S2为2个测量通道测量获得的信号的比值,可通过锁相放大器测量得到的交流电压结合低噪声放大器增益设置,精确测定。结合标定源外推出的表面真实温度,即可得到系统标定系数:
(6)
由式(6)不难看出,精确标定CALP参数的关键在于样品表面真实温度T的精确获得。换言之,通过实验设计已知表面真实温度的标定源,即可实现参数的高精度标定。
3 实验装置
3.1 高精度表面温度标定源
标定源中加热样品由化学气相合成碳化硅陶瓷(CVC-SiC)制成,该材料是一种潜在的高温发射率量值传递标准材料,具备耐高温、不易氧化、辐射特性较为稳定等特点。标定样品内置一等热电偶,溯源至我国基础测温基准。高精度数字表与热电偶连接,可求出热电偶与样品接触点的温度,从而外推出标定样品表面真实温度。
样品内部热电偶布置方案如图1,将2只一等标准热电偶分别插入标定源所用样品事先预置的两个具有深度差的孔中。由于样品是由同一种材料均匀制成,导热系数随温度变化,根据文献[19], SiC材料导热系数随温度变化关系为
K=0.396-1.633×10-4T
(7)
实际测量中热电偶1和热电偶2温度差值约为2 K,通过计算,在本实验温度变化范围内导热系数相对变化量为0.1%,因此可近似认为样品温度呈线性分布。
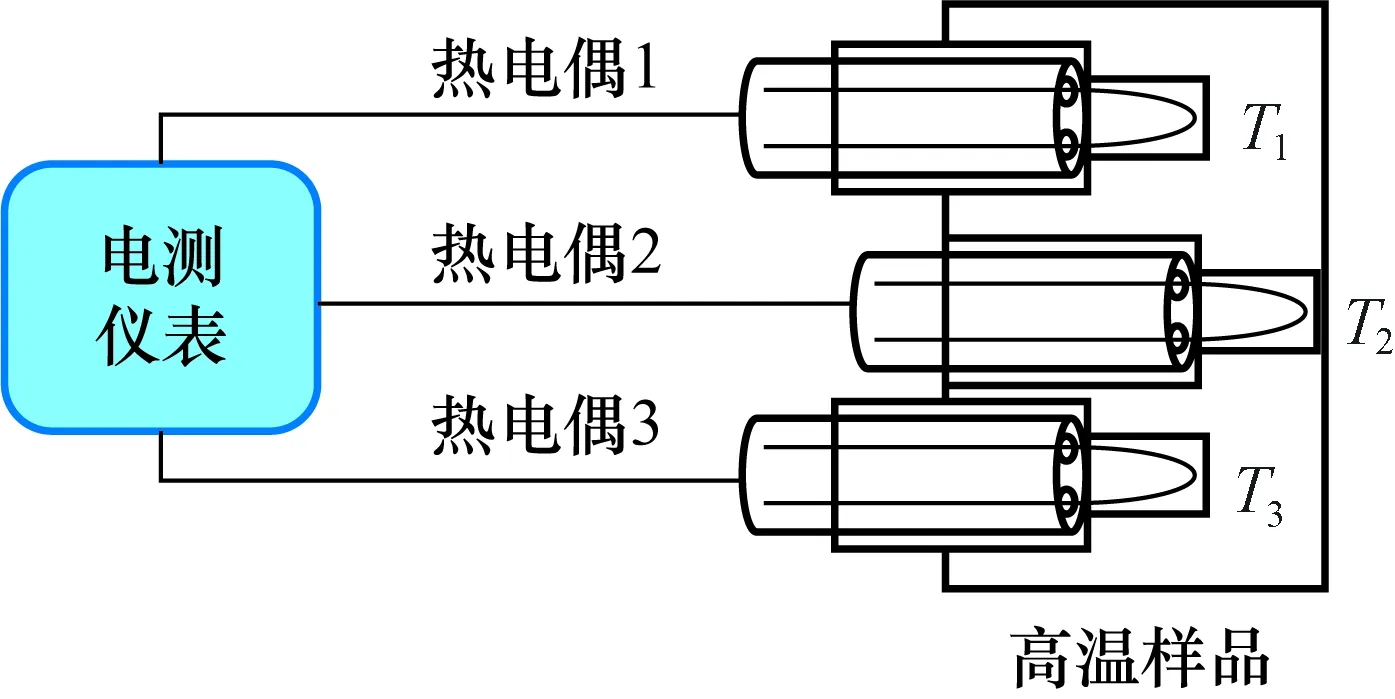
图1 样品内部热电偶布置方案Fig.1 Layout plan of sample internal thermocouple
热电偶1测得的温度值为T1,热电偶2测得的温度值为T2,热电偶1和热电偶2深度差为b,热电偶2距离标定样品表面的距离为a。
温度外推计算方法如式(8),求得标定源表面真实温度T:
(8)
将所得表面真实温度代入已推导出的理论模型,完成标定。
3.2 辐射温度计
本文所用的传递级标准辐射温度计为TRT IV.82型辐射温度计,测量波长为3.9 μm,这个波段是国家计量领域标定实验常用的中红外波段。用NIM的传递级标准辐射温度计作为标准器,设置辐射温度计内的发射率参数为1后测量的结果为物体的亮度温度。使用传递级标准辐射温度计对标定样品进行表面辐射温度测量,验证样品表面辐射温度稳定性及均匀性。
3.3 双波长红外激光主动式测温系统
基于双波长激光-材料相互作用下的光热效应理论,采用反序波长探测和相敏检测技术,设计并搭建一套基于光热效应的双波长红外激光主动式测温系统,如图2所示。本文所搭建的双波长红外激光主动式测温系统主要由红外激光光源子系统、成像与瞄准子系统和光电探测子系统构成。其中,红外激光光源子系统由激光器和函数发生器构成;成像与瞄准子系统由光学镜头和光纤构成;光电探测子系统主要由2个与激光波长对应的窄带滤光片辐射计、可调增益放大器和锁相放大器构成。
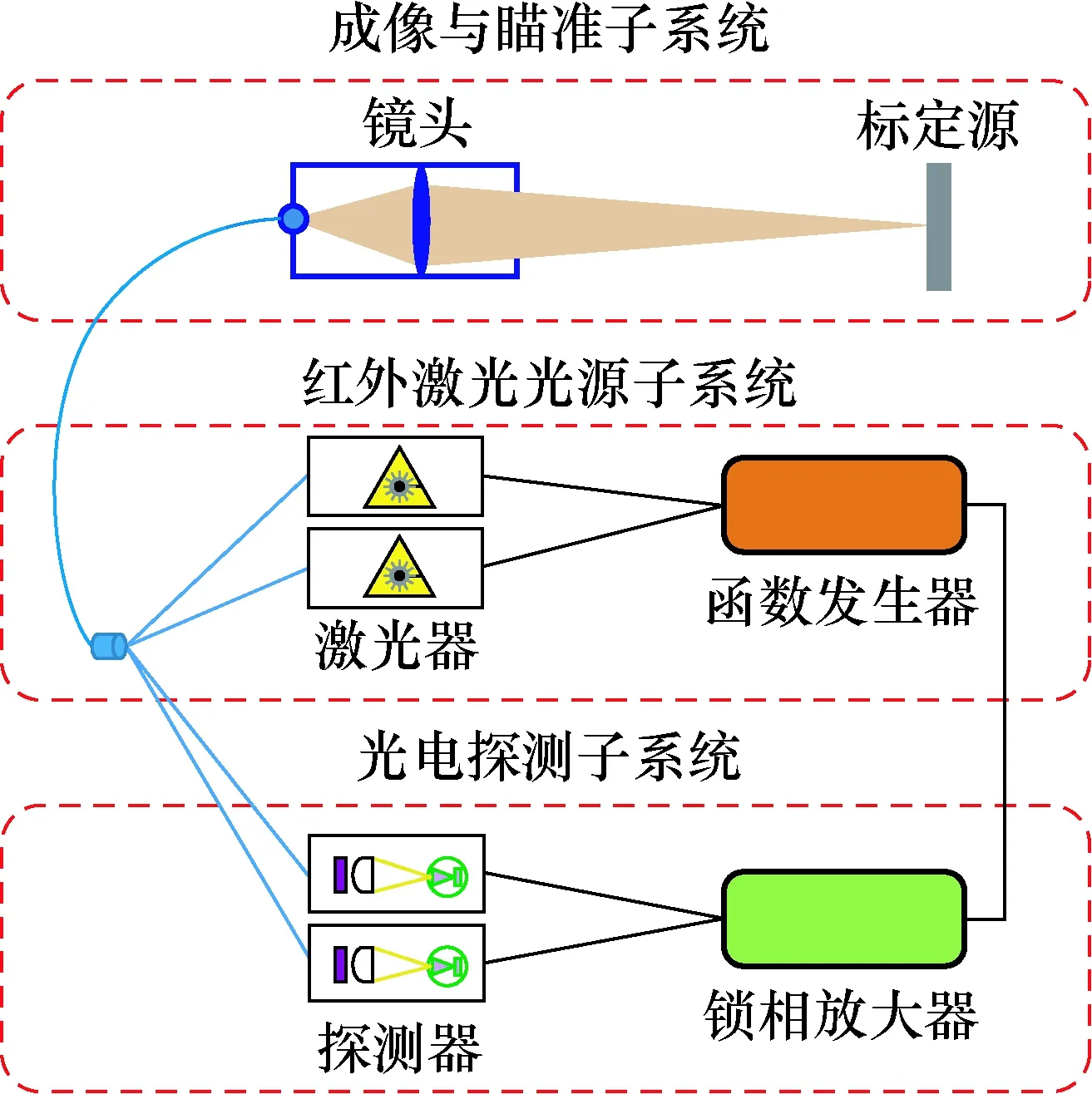
图2 主动式双波长红外激光测温系统Fig.2 Active dual-wavelength infrared laser thermometry system
基于相敏检测技术,可精准获取待测目标面温升导致的交流信号。调制激光器,使其产生一定频率的激光并投射至目标面,目标面出现相应的温升,该温升信号经系统光路投射至光电探测系统,在光热效应的作用下,探测器产生同频率的交流信号,探测器将该信号输出至锁相放大器,锁相放大器根据函数发生器的调制参考信号进行相敏检波处理,准确获得来自目标面的交流信号,该信号由数据采集系统采集并进行处理。
4 实验结果
4.1 标定源稳定性验证
本文标定源在20 min内的真实温度和亮度温度变化测量结果如图3所示。其中,定标源中心的真实温度由热电偶测量值外推获得;定标源中心亮度温度由辐射温度计测量得到。采样时间间隔为1 s。
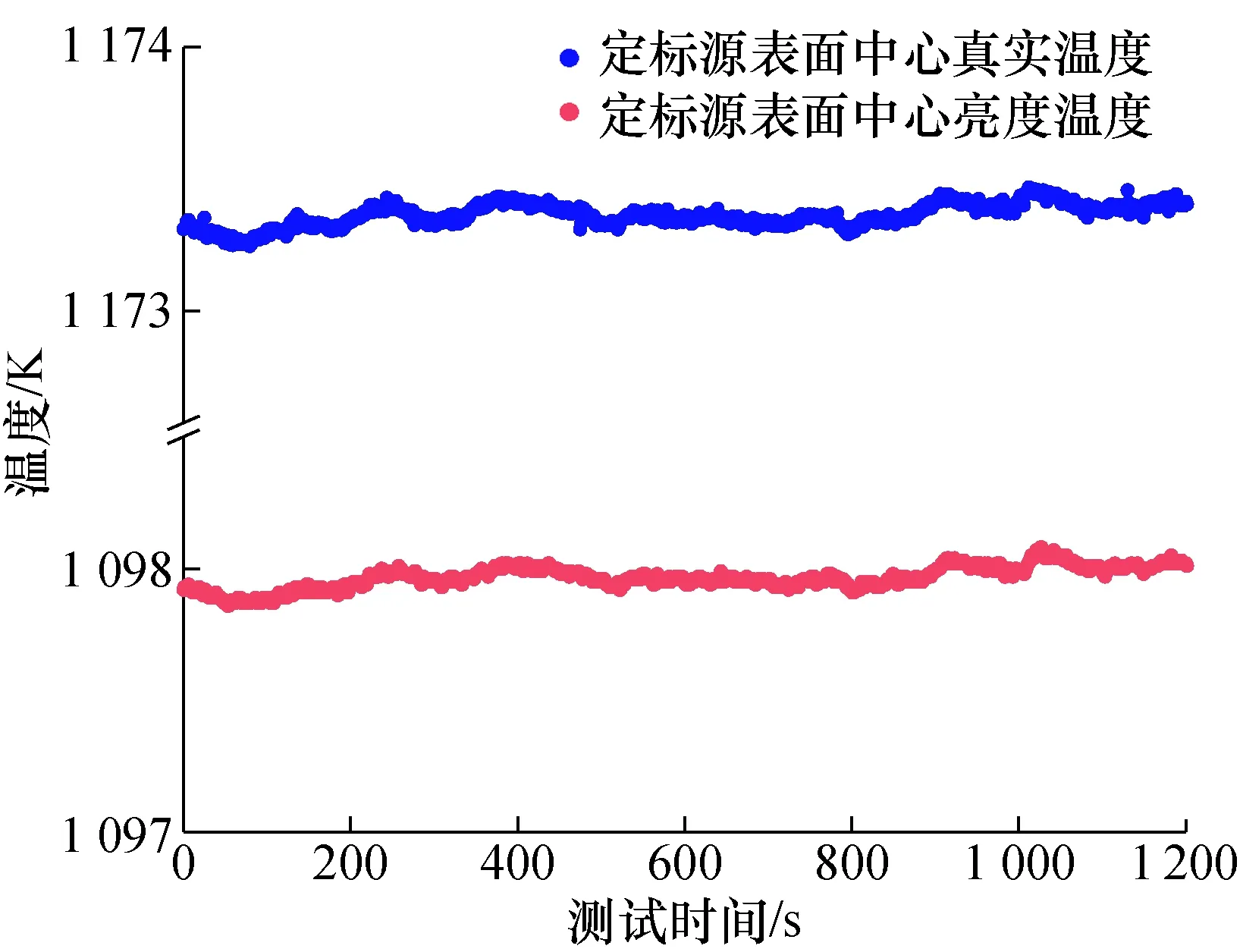
图3 温度稳定性实验结果Fig.3 Temperature stability test results
由图3可知:标定源的真实温度与标准辐射温度计所测亮度温度变化趋势一致,证明外推表面真实温度的可靠性良好;表面真实温度20 min内最大偏差为0.22 K,标准偏差为0.04 K,相对标准偏差0.01%,证明所采用标定源稳定性良好,适合用于高精度标定。
4.2 标定源均匀性验证实验
本文使用接触法和辐射法2种方案进行标定源均匀性验证。
接触法的均匀性测量结果如图4所示。其中,两端热电偶温度偏差指的是样品两侧等深度的热电偶1与热电偶3所测温度之差,采样间隔为1 s。由图4可知,标定源在1 173 K时两端热电偶温度偏差绝对值小于0.81 K。
辐射法的测量方案如图5所示,将标准辐射温度计置于二维精密步进电机上,在标定样品的水平(X)方向和竖直(Y)方向上进行循环扫描测量,相邻扫描点间隔为2 mm,重复3次。
辐射法的均匀性测量结果分别如图6和图7所示。其中,图6展示的是标准辐射温度计3测量各点温度相对于中心平均温度T0的差值;图7展示的是对应的相对偏差δ,δ计算式为[20]:
(9)
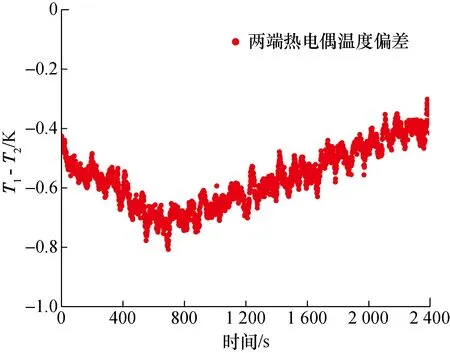
图4 两端热电偶温度偏差Fig.4 Temperature deviation between two thermocouples
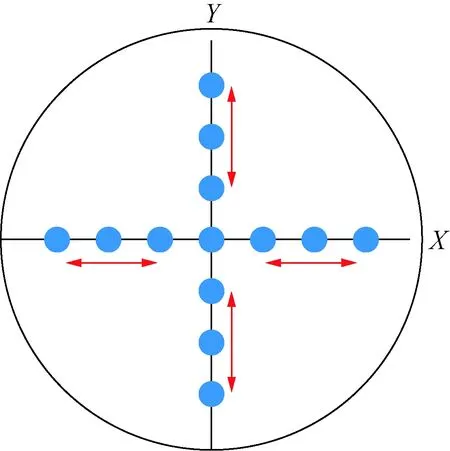
图5 均匀性扫描方案Fig.5 Uniformity scanning scheme
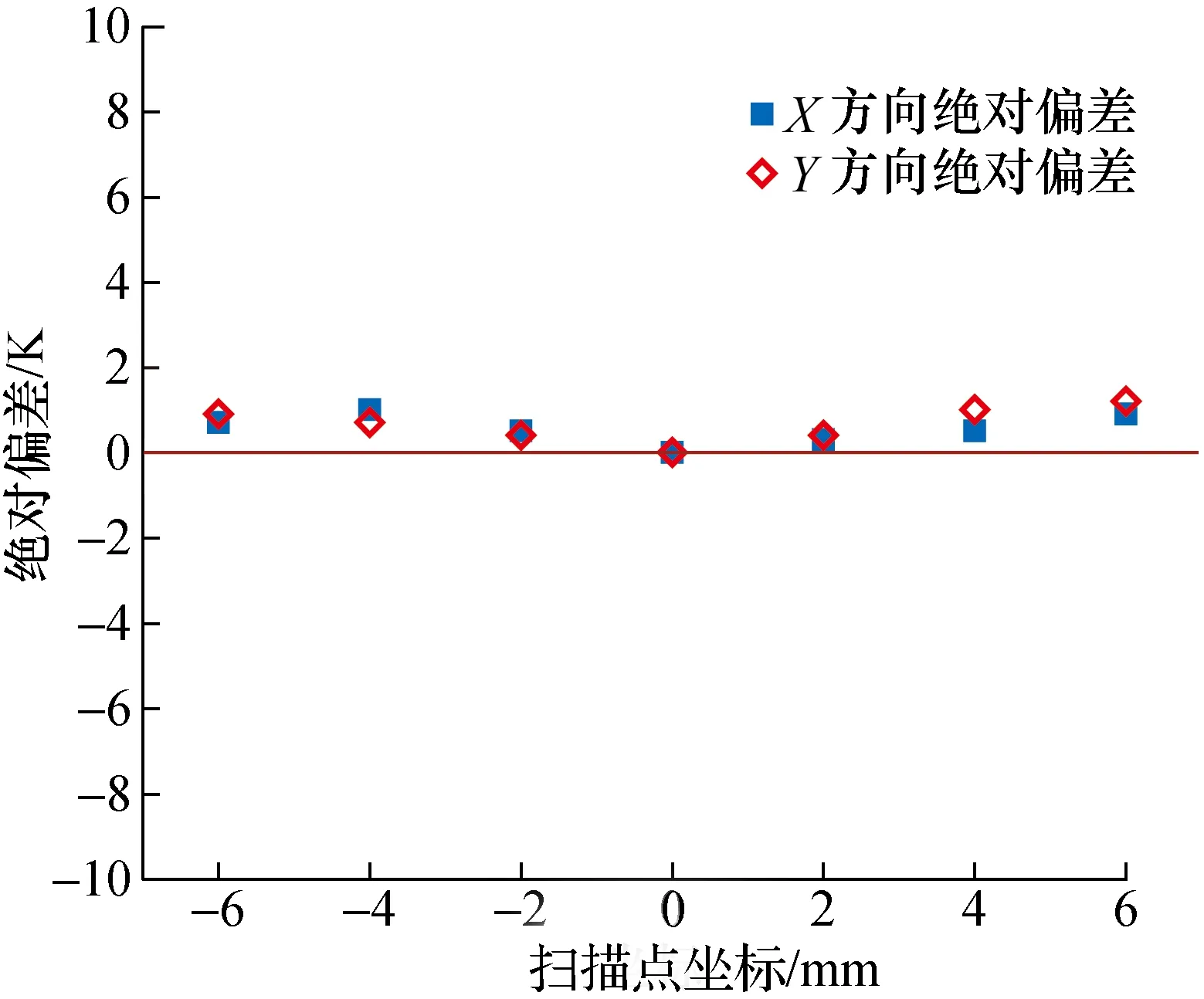
图6 X和Y方向各点绝对偏差Fig.6 Absolute deviation of dots in the X and Y directions
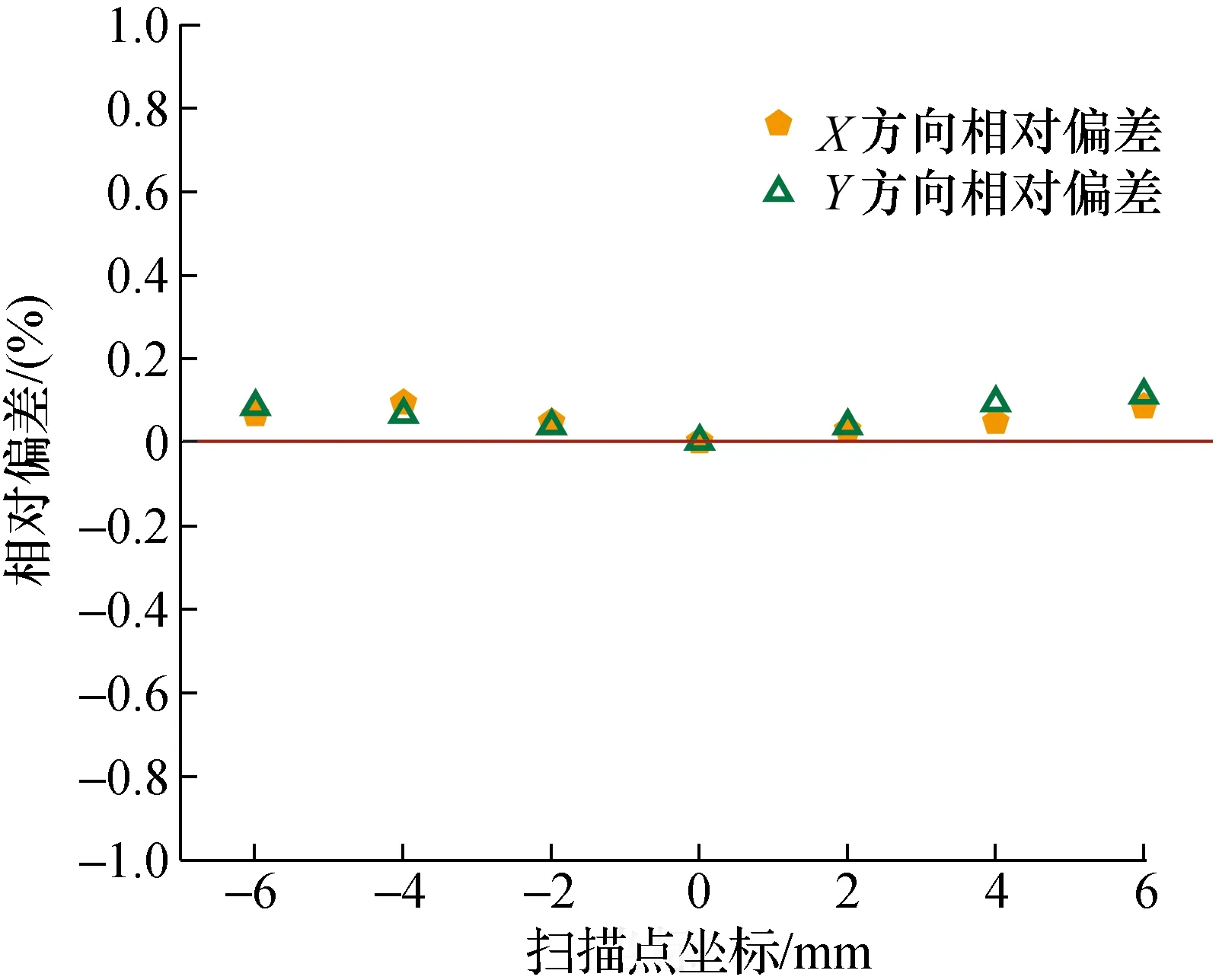
图7 X和Y方向各点相对偏差Fig.7 Relative deviation of dots in the X and Y directions
经实验测量,标定源表面各点温度的标准偏差为0.34 K,相对标准偏差为0.03%。其中,X方向上各点的标准偏差为0.35 K,相对标准偏差为0.03%;Y方向上各点的标准偏差为0.42 K,相对标准偏差为0.04%。该结果表明:标定源表面温度均匀性良好,能够满足双波长红外激光测温系统标定要求。
4.3 采集信号的稳定性
将所搭建标定源应用于双波长红外激光主动式测温系统,检验采集信号的稳定性,从而进一步评估所选标定源的可靠性。两路测量通道在不同目标温度下锁相放大器所采集到的信号如图8所示,每个温度点采集60组数据,时间间隔为1 s。
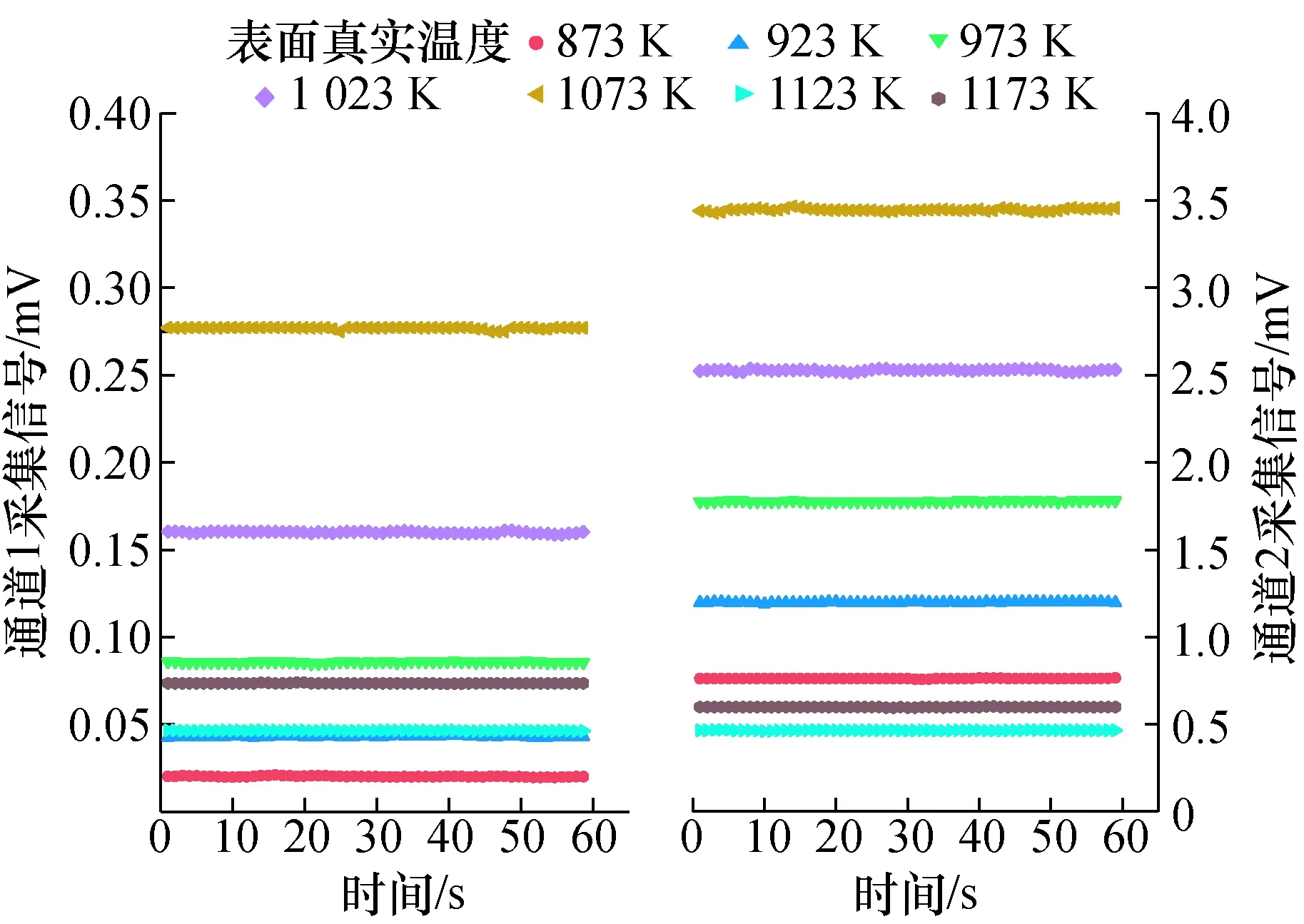
图8 两路通道在不同温度下的测量信号Fig.8 Measurement signals from two channels at different temperatures
需要说明的是,图8中1 123 K、1 173 K信号值相对较低是因为该温度下系统所用放大器过载,因此将放大倍率由108调整到107,导致采集信号偏低,但因为是两路通道同时调节,所以并不影响最终温度的计算。
两路测量信号的相对标准偏差如图9所示。可以看出,通道1在923 K及以上锁相采集信号的相对标准偏差<0.7%,且随着温度的升高,相对标准偏差呈下降趋势;通道2在873 K及以上锁相采集信号的相对标准偏差<0.4%,整体趋势较为稳定。
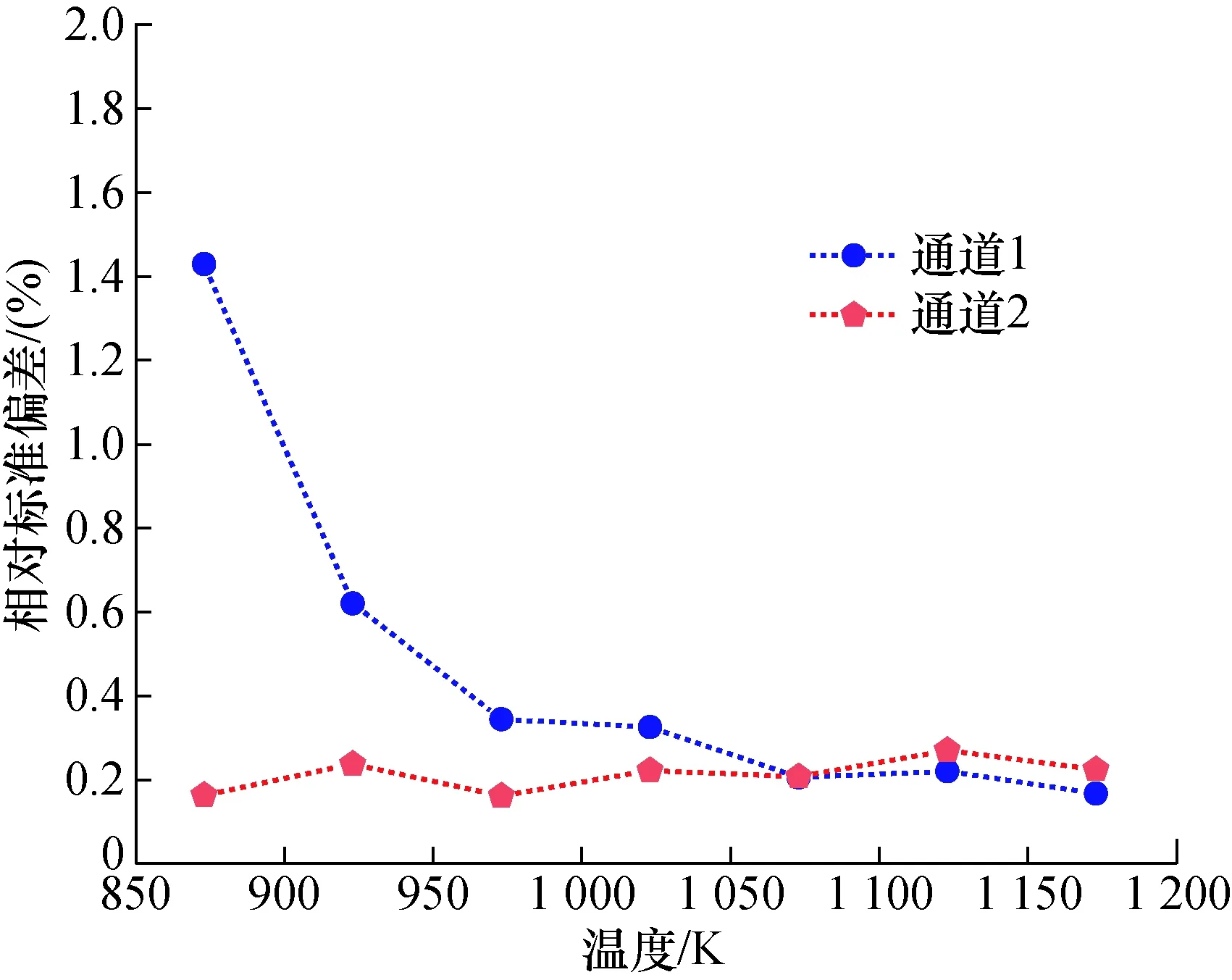
图9 两路测量信号的相对标准偏差Fig.9 Relative standard deviation of two measurement signals
由图9可知,应用标定源后,通道1的偏差对于整个采集系统贡献在温度较低时更为明显,随着测量温度的升高,通道1信号相对标准偏差更小,稳定性更优,因此整个系统随测量温度上升稳定性更好,从而再次证明了标定源性能良好。
4.4 标定源可靠性验证
依据红外激光主动式测温系统标定原理,开展了红外激光主动测温标定实验,并对标定源的可靠性进行了验证分析。由标定公式(6)可知,标定源在不同温度下,两个波长滤光片辐射计测量信号经锁相放大器相敏检波处理后的信号比值(S1/S2)与光谱辐射亮度一阶导数比值(L′(λ1)/L′(λ2))呈线性的函数关系。通过对实验结果计算发现,如果应用单温度点标定方法,各温度点标定系数相对偏差最大达到9.99%,这将使得温度测量产生显著的误差,在1 173 K时,偏差甚至会达到20 K以上。因此,本文采用了拟合曲线斜率的标定方法。
确定了标定方法后,选择合适的标定源样品材料十分关键。因此,本文对可能适用于标定的4种不同材料样品进行了测试。由图10可知,材料1(即SiC)的R2最大,拟合度最佳,其它3种材料的测试结果在各温度点下无规律地分布在材料1拟合曲线的两侧。证明了材料1不但相较于其它材料的样品具备更好稳定性,而且具备一定的普适性。因此使用该种材料制作标定源对双波长红外激光主动式测温系统进行标定。
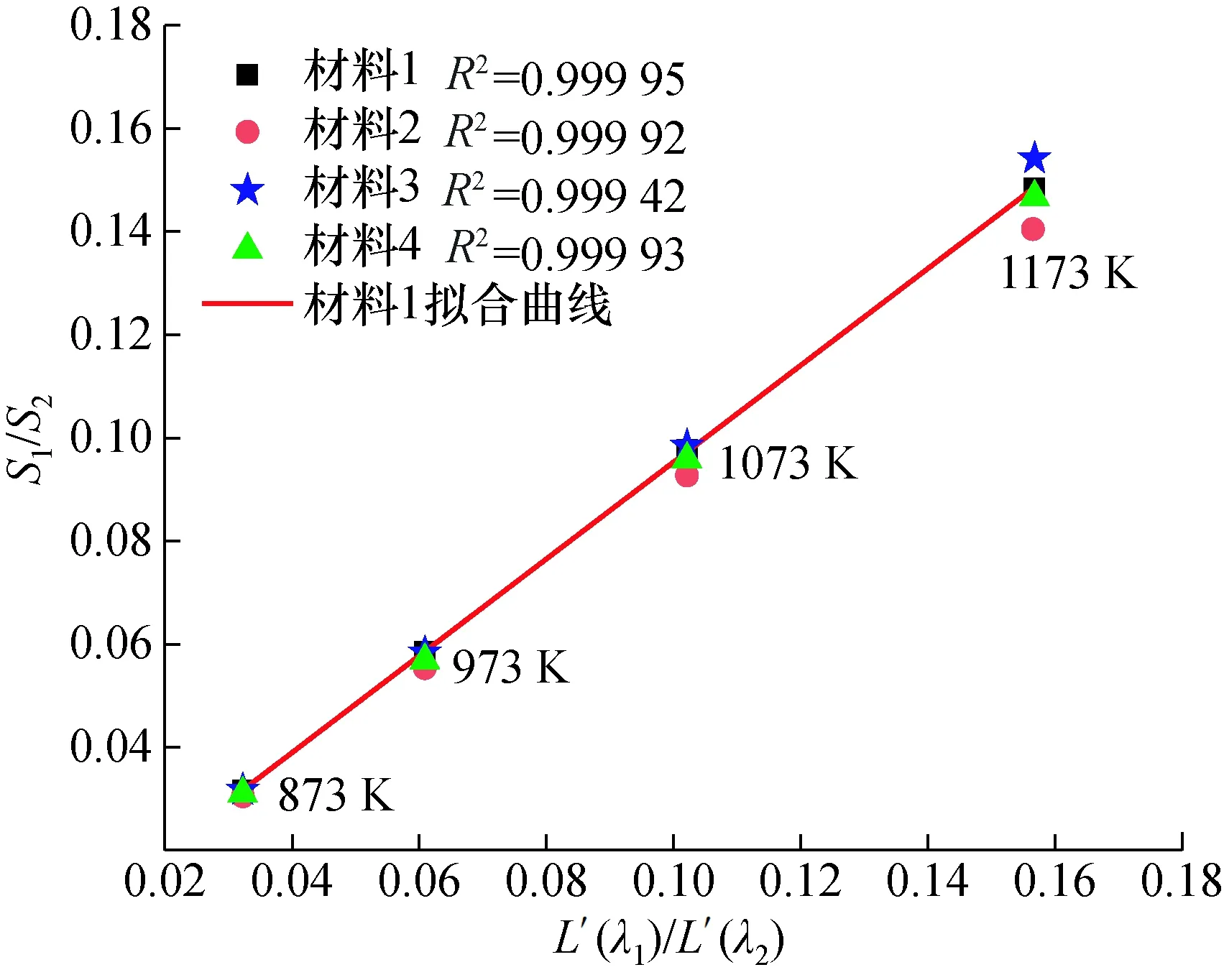
图10 不同材料拟合结果Fig.10 Fitting results of different materials
本文在确定了标定源的应用材料后,对其在873~1 173 K温区范围内进行了3次重复标定试验,结果如图11,经计算标定系数为0.774 8。
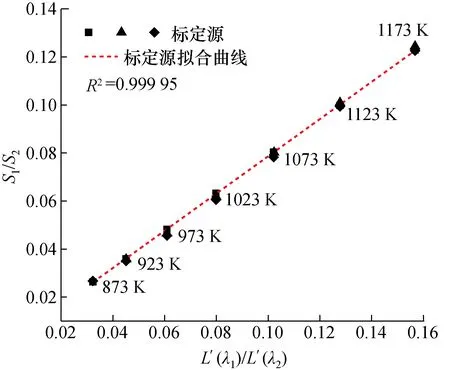
图11 重复标定实验Fig.11 Repeated calibration experiment
经计算,3次标定实验标定系数相对标准偏差为0.28%,对标定源应用拟合曲线斜率标定方法重复性良好,因此可将标定源进一步应用到后续的主动式双波长红外激光测温实验。
5 结 论
本文基于双波长红外激光主动式测温原理,搭建了主动式双波长红外激光测温标定源,开展了标定实验研究。结果表明:
1) 稳定性方面,标定源表面真实温度在20 min内标准偏差为0.04 K,相对标准偏差为0.01%;均匀性方面,标定源表面各点温度的标准偏差为0.34 K,相对标准偏差为0.03%。证明本文所建立的标定源温度稳定性、均匀性良好。
2) 信号采集方面,锁相放大器数据采集结果在923 K及以上的相对标准偏差<0.7%,且随着温度的升高稳定性更优。
3) 通过线性拟合,发现输出信号比值与光谱辐射亮度一阶导数的比值具有良好的线性关系;标定源3次重复试验标定系数相对标准偏差为0.28%,标定系数重复性良好。
综上所述,所搭建主动式双波长红外激光测温标定源性能良好,可应用于未来的主动式双波长红外激光测温实验。

