融入曲率尺度空间算法的图像配准方法

章 盛,李培华,钱名思,刘玉莉

(1.中航华东光电有限公司,安徽 芜湖 241002；2.安徽省现代显示技术重点实验室,安徽 芜湖 241002；3.国家特种显示工程技术研究中心,安徽 芜湖 241002；4.特种显示国家工程实验室,安徽 芜湖 241002)

1 引 言

图像配准普遍应用在遥感图像配准[1]、医学图像配准[2]和全景显示[3]等领域,其中2006年Herbert Bay等人提出的加速稳健特征(Speeded Up Robust Features,SURF)算法[4]是经典的图像配准算法,其以尺度不变特征变换(Scale Invariant Feature Transform,SIFT)算法[5-6]为基础对图像特征的提取和描述进行了优化,结果是在保持了平移、旋转与尺度等变化不变性的前提下提升了执行效率。近年来,科研者根据SURF算法存在实时性问题,提出了将角点提取算法融入传统SURF算法的想法,互取优势,例如葛盼盼等人于2014年提出的Harris-SURF算法[7],彭勃宇等人于2015年提出的SUSAN-SURF算法[8],张敬丽等人于2016年提出的MIC-SURF算法[9],产叶林等人于2019年提出的FAST-SURF算法[10],四种改进算法最终得到的结论是在图像配准实时性方面得到了改善；同时由于SURF算法具备很好的稳健性,许金鑫等人于2017年使用形态学边缘检测算法对待配准图像进行预处理,然后利用SURF算法进行异源图像的配准,并将优化SURF算法应用于电气设备图像的配准,为异源图像的配准提供了一种途径[11]；2018年,王民等人利用压缩感知原理[12]对SURF算法生成的描述子向量进行降维处理,提升了实时性并应用于手语关键帧的配准[13]。

针对实时性要求比较高的应用场景,传统SURF算法表现出其在实时性方面的不足,本文首先针对图像角点特征提取耗时长的问题,使用曲率尺度空间(Curvature Scale Space,CSS)算法[14]提取图像角点特征,然后针对图像角点特征匹配耗时长的问题,使用改进SURF描述子、改进相似性距离算法和随机采样一致性((Random Sample Consensus,RANSAC)[15]算法对图像角点特征描述子的形成和匹配进行改进,最终得到CSS-SPP-SURF算法。

2 CSS-SPP-SURF算法

CSS-SPP-SURF算法按照实现流程分成三个步骤:①图像角点特征的提取；②图像角点特征描述子向量的生成和降维；③图像角点特征的匹配。CSS-SPP-SURF算法的实现流程框图如图1所示。

2.1 图像角点特征的提取

Mokhtarian和Suomela团队于1998年提出的一种基于曲线曲率的图像角点特征提取算法,即CSS算法,其是在Canny算法[16]的基础上延伸的算法,该算法提取图像角点特征分为三步:

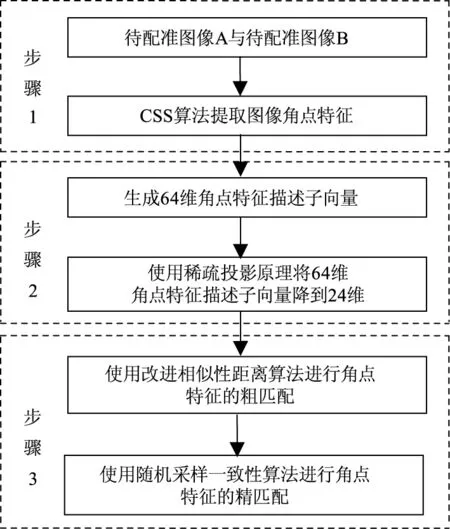
图1 CSS-SPP-SURF算法的实现流程框图

①采用Canny算法生成边缘轮廓图像；②在尺度空间的低尺度上使用局部曲率极大值提取图像角点特征,并向高尺度跟踪定位这个图像角点特征；③与T型角点特征作比较剔除相近的角点特征中一个。曲线的曲率κ的函数表达式的如式(1)所示:

κ(μ,σ)=

(1)

其中,κ(μ,σ)表示曲线的曲率；Xμ(μ,σ),Xμμ(μ,σ)分别表示X(μ,σ)的一阶、二阶导数；Yμ(μ,σ),Yμμ(μ,σ)分别表示Y(μ,σ)的一阶、二阶导数；μ表示弧长参数；σ表示尺度因子。

针对公式(1),X(μ,σ)和Y(μ,σ)的一阶、二阶导数的表达式分别如式(2)～(5)所示:

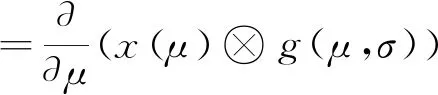
=x(μ)⊗gμ(μ,σ)

(2)

=x(μ)⊗gμμ(μ,σ)

(3)

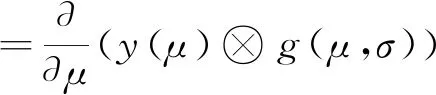
=y(μ)⊗gμ(μ,σ)

(4)

=y(μ)⊗gμμ(μ,σ)

(5)

其中,Xμ(μ,σ),Xμμ(μ,σ)分别表示X(μ,σ)的一阶、二阶导数；Yμ(μ,σ),Yμμ(μ,σ)分别表示Y(μ,σ)的一阶、二阶导数；x(μ)和y(μ)分别表示曲线上点的横坐标和纵坐标；g(μ,σ)表示以尺度因子σ为参数的高斯函数;μ表示弧长参数;σ表示尺度因子;⊗表示卷积运算;gu(μ,σ),guu(μ,σ)分别表示g(μ,σ)的一阶、二阶导数。

2.2 改进SURF描述子

CSS-SPP-SURF算法生成图像角点特征描述子向量分为两个阶段,阶段一是利用Haar小波生成64维图像角点特征描述子向量,阶段二是利用稀疏投影原理将64维图像角点特征描述子向量降维到24维,仿真实验中发现降维到12维,图像角度特征的匹配速度有一定提升,但匹配效果不太理想,综合考虑选择降维到24维。

针对阶段一得到64维图像角点特征描述子向量,假定其为K,首先利用小波变换基矩阵Ψ将64维描述子向量转换为64维稀疏矩阵Y,然后利用稀疏投影矩阵R∈R24×64将64维稀疏矩阵Y转换为24维测量向量K′,最后将得到的24维测量向量K′作为图像角点特征描述子向量,如式(6)所示:

K′=RY=RΨK

(6)

其中,K′表示24维测量向量;R表示24×64维的稀疏投影矩阵;Y表示64维的稀疏向量;Ψ表示64×64维的小波变换基矩阵;K表示64维的图像角点特征描述子向量。

2.3 图像角点特征的匹配

图像角点特征的匹配分为两个阶段,阶段一使用改进的相似性距离算法进行粗匹配；阶段二使用RANSAC算法进行精匹配。

阶段一假设对图像L与图像R的图像角点特征进行粗匹配实验,设定图像L的图像角点特征描述子向量为Ui(x1,x2,x3,…,x22,x23,x24),图像R的图像角点特征描述子向量为Vj(y1,y2,y3,…,y22,y23,y24),整个匹配实验过程分为三个步骤:

步骤1:图像L到图像R采用曼哈顿距离进行相似性距离度量,曼哈顿距离定义式如式(7)所示,同时相似性距离的最小值和次最小值的比值满足公式(8),遍历图像L的图像角点特征集U,得到匹配图像角点特征集A。

(7)

其中,d(Ui,Vj)表示图像角点特征之间的相似性距离;xm表示图像L中图像角点特征描述子向量的元素;ym表示图像R中图像角点特征描述子向量的元素。

(8)

其中,d(Ui,V1j)、d(Ui,V2j)分别表示特征集U中的特征Ui与特征集V中的最近邻特征V1j、次最近邻特征V2j的相似性距离;Th1表示阈值,本文设定Th1的值为0.75。

步骤2:图像R到图像L采用欧式距离进行相似性距离度量,欧式距离定义式如式(9)所示,同时相似性距离的最小值和次最小值的比值满足式(10)所示,遍历图像R的图像角点特征集V,得到匹配图像角点特征集B。

(9)

其中,d(Vj,Ui)表示图像角点特征之间的相似性距离;ym表示图像R中图像角点特征描述子向量的元素;xm表示图像L中图像角点特征描述子向量的元素。

(10)

其中,d(Vj,U1i)、d(Vj,U2i)分别表示特征集V中的特征Vj与特征集U中的最近邻特征U1i、次最近邻特征U2i的相似性距离;Th2表示阈值,本文设定Th2的值为0.75。

步骤3:比较匹配图像角点特征集A与B,选取完全相同的匹配图像角点特征组成备用的匹配图像角点特征集M。

阶段二采用RANSAC算法对阶段一得到的备用匹配图像角点特征集M进行进一步提纯,得到最终的匹配图像角点特征集F。

3 仿真实验

实验仿真软件为MATLAB R2014a,实验仿真硬件为计算机,计算机的中央处理器配置是Intel Core i3-3240 CPU @ 3.40GHz (4 CPUs)、内存配置是4096MB RAM、操作系统配置是Windows 7 旗舰版32位。

仿真实验分为两个阶段,第一阶段选用立体匹配库中的Venus可见光图像、异源融合库中的Jeep_in_Smoke红外图像和Normal Medical Database库中的手部CT医学图像作为仿真实验一图像,其中图2(a) ～ (d)是立体匹配库中的Venus源、右视、形变和旋转图像,像素大小为434×383；图2 (a2) ～ (d2)是异源融合库中Jeep_in_Smoke红外源、右视、形变和旋转图像,像素大小为580×450；图2 (a3) ～(d3)是Normal Medical Database库中的手部CT医学源、右视、形变和旋转图像,像素大小为240×256；以验证CSS-SPP-SURF算法对不同源图像的可行性。第二阶段选用立体匹配库中不同规模的图像库作为仿真实验二图像,立体匹配库中每对待配准图像仅有源、右视两张图像,以验证CSS-SPP-SURF算法的普遍适应性。

图2 实验一的待配准图像

仿真实验一使用传统SIFT算法、传统SURF算法、Forstner-SURF算法、Harris-SURF算法、Trajkovic-SURF算法与CSS-SPP-SURF算法对实验一图像进行图像配准实验,实验步骤分为三步:①图2(a)分别与图2(b)～(d)进行图像配准实验；②图2(a2)分别图2(b2)～(d2)进行图像配准实验；③图2(a3)分别与图2(b3)～(d3)进行图像配准实验,最终得到图像角点特征的检测结果图如图3(a)～(r4)所示,图像角点特征的匹配结果图如图4(a)～(i6)所示。

仿真实验一为了比较CSS-SPP-SURF算法与传统SIFT算法、传统SURF算法、Forstner-SURF算法、Harris-SURF算法、Trajkovic-SURF算法之间的效率,选取待配准图像的角点特征数目、角点特征匹配数目、角点特征正确匹配数目、图像配准准确率、图像配准时间与图像配准时间下降率共六个指标作为评价依据,其中图像配准准确率和图像配准时间下降率的计算公式如式(11)、(12)所示,仿真实验数据对比分析图如图5(a)～(f)所示,通过图5(d)可知,CSS-SPP-SURF算法与传统SIFT算法、传统SURF算法、Forstner-SURF算法、Harris-SURF算法、Trajkovic-SURF算法相比,在图像配准的准确率方面相当。通过图5(f)可知,CSS-SPP-SURF算法与传统SIFT算法、传统SURF算法、Forstner-SURF算法、Harris-SURF算法、Trajkovic-SURF算法相比,在图像配准的速度方面具有一定的优势。

(11)

(12)

图3 图像角点特征的提取结果图

其中,图3(a)～(r)、(a2)～(r2)、(a3)～(r3)、(a4)～(r4)表示使用传统SIFT算法、传统SURF算法、Forstern-SURF算法、Harris-SURF算法、Trajkovic-SURF算法与CSS-SPP-SURF算法分别对实验一待配准图像中源图像、右视图像、形变图像、旋转图像的角点特征提取结果图。

图4 图像角点特征的匹配结果图

其中,图4(a)～(i)、(a2)～(i2)、(a3)～(i3)、(a4)～(i4)、 (a5)～(i5)、(a6)～(i6)分别表示使用传统SIFT算法、传统SURF算法、Forstern-SURF算法、Harris-SURF算法、Trajkovic-SURF算法与CSS-SPP-SURF算法对实验一待配准图像的角点特征匹配结果图。源-右视表示源图像和右视图像之间的配准、源-形变表示源图像和形变图像之间的配准和源-旋转表示源图像和旋转图像之间的配准。

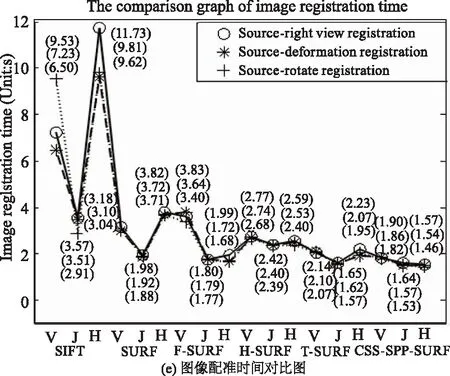
图5 图像配准的对比分析图

图5中，V表示Venus可见光图像；J表示Jeep_in_Smoke红外图像；H表示手部CT医学图像；SIFT表示传统SIFT算法；SURF表示传统SURF算法；F-SURF表示Forstern-SURF算法；H-SURF表示Harris-SURF算法；T-SURF表示Trajkovic-SURF算法；CSS-SPP-SURF表示CSS-SPP-SURF算法。其中，图5(a)～(f)表示使用传统SIFT算法、传统SURF算法、Forstern-SURF算法、Harris-SURF算法、Trajkovic-SURF算法与CSS- SPP-SURF算法对实验一图像的特征提取数目、特征匹配数目、正确特征匹配数目、配准准确率、配准时间和配准时间下降率的对比分析图。

仿真实验二首先从立体匹配库中分别选择100、200、300、400对图像作为四种不同规模待配准图像库,然后使用传统SIFT算法、传统SURF算法、Forstern-SURF算法、Harris-SURF算法、Trajkovic-SURF算法与CSS-SPP-SURF算法对四种不同规模待配准图像库进行配准,并对评价指标进行记录并统计,统计结果如表1所示,最后对表1的仿真实验数据进行分析得到两点结论:①CSS-SPP-SURF算法与传统SIFT算法、传统SURF算法、Forstern-SURF算法、Harris-SURF算法、Trajkovic-SURF算法相比,图像配准准确率相当；②图像配准时间分别降低了73.61%、43.27%、44.54%、34.31%与8.05%。

表1 不同规模图像集的图像配准时间、准确率比较

表1中，SIFT代表传统SIFT算法；SURF代表传统SURF算法；F-SURF代表Forstner-SURF算法；H-SURF代表Harris-SURF算法；T-SURF代表Trajkovic-SURF算法；C-SURF代表CSS-SPP-SURF算法；时间指图像配准时间,单位是秒,准确率指图像配准准确率,单位是%。

4 结 论

本文提出了CSS-SPP-SURF算法,该算法使用CSS算法、改进SURF描述子、改进相似性距离算法和RANSAC算法对传统SURF算法进行改进,解决了其图像特征检测和匹配耗时长的问题。通过仿真实验发现两点:①CSS-SPP-SURF算法对可见光、红外与医学图像同样有效；②通过对立体匹配库实验说明了该算法对于实时性要求比较高的应用场景具有普遍有效性。