高超声速再入目标动态红外辐射特性修正计算

刘太阳,刘 辉,邹 坚

(1.空军预警学院,湖北 武汉 430019；2.解放军32228部队,江苏 南京 211132)

1 引 言

高超声速飞行器能于临近空间做长时间、远距离的高超声速(Ma≥5)飞行,并具备大规模的轨道机动能力,因而具备极强的突防性能[1]。在高超声速飞行器目标特性研究中,目标红外辐射特性的计算和分析是重要内容,其对于高超声速目标的早期预警和跟踪识别具有根本性的支撑意义。

但是由于高超声速飞行器飞行环境的复杂多变,高速尤其高超声速条件下会出现各种复杂的流体现象及模态,对其特性分析构成较大的干扰和困难。相比于传统航空领域的亚音速或超音速流动,高超声速流动会出现诸如激波与边界层的相互干扰、边界层传热传质、化学反应以及烧蚀等特殊流动现象,具有薄激波层、熵层、黏性干扰效应、高温效应以及低密度流动效应等显著特征[2-3]。这些特殊的流体现象和热/化学平衡和非平衡状态,导致高超声速再入飞行器的气动加热模型非常复杂[3-5]。尤其在实装及现场试验条件有限的情况下,相应气动加热及辐射效应的精确计算更加困难。

本文旨在探索一种结合工程计算经验的红外特性分析方法,基于传统气动加热理论,考虑大气环境参数变化特点,探索应用大气密度作为高度修正因子构建目标关键点的气动加热温度计算公式,为高超声速目标的红外辐射特性分析提供支撑,满足相关分析论证和实验规划的计算需求。

2 传统气动加热理论

当高速气流流过物体表面时,由于摩擦、压力改变和速度受到阻滞等原因,会使物体周围的空气温度升高。这种热量通过热传导和辐射等方式传给物体,而使物体温度升高的现象称为空气动力加热。气流速度愈高,气动加热现象愈严重,气动加热造成的飞行器表面的温度变化可以用如下公式计算[6-8]:

(1)

式中,Ts为飞行器表面温度；T0为飞行环境的大气温度；k为恢复系数,其值取决于飞行器所处的大气层的气流流场,层流取值约为0.82,紊流取值约为0.87；γ为空气的定压热容量和定容热容量之比,通常取值约为1.3；Ma为以马赫数表示的飞行器飞行速度,1Ma的速度即为声音在空气中的传播速度(对于航空飞行器而言,此值约为340 m/s)。

典型工程计算中,航空飞行器表面因空气动力加热的温度通常可以采用如下的工程经验公式来计算[7]:

Ts=T0[1+0.164·Ma2]

(2)

公式(2)中Ma前面的系数对应公式(1)中的恢复系数k以及空气的定压热容量和定容热容量之比γ。

以上传统气动加热理论主要适用于飞行在20 km以下大气层内的航空目标。此类目标主要飞行在对流层顶部和平流层底部,飞行器受到大气层的气动加热作用而导致其温度高于环境温度。

3 高超声速再入目标气动加热模型

在高超声速飞行器的飞行过程中,其将长时间遭遇复杂多变的空气动力加热环境,涉及高超声速稀薄空气流、高温下的气体化学/热非平衡流动,稀薄气体效应和非平衡气体效应都比较显著,传统经典的连续流动理论和化学平衡假设均已失效[9]。在公式(1)和公式(2)中,除环境温度T0随海拔高度变化外,声音传播速度、恢复系数k以及空气的定压热容量和定容热容量之比γ也随大气参数变化而变化,需要根据大气模型数据(包括海拔高度、大气温度、大气密度、大气压强等参数)进行修正。

3.1 基本大气及声速模型

当前理论研究中,应用的主要是国际标准大气模型,其基本原则为选取地球中纬度地区的全年实际大气参数的统计均值作为标准大气参数,且认为大气是相对湿度为零的完全气体[10]。实用中,较为经典的国际标准大气模型是美国标准大气(1976),其对不同高度的大气密度、气压、温度以及声速进行分段建模,并提供了较为详细的计算方式。典型高度下的大气参数如表1所示。

表1 典型高度下的大气参数(1976标准大气)

气动加热计算中,大气密度和当地声速是较为关键计算要素。基于模型对其进行计算,得出基本结果如图1所示。

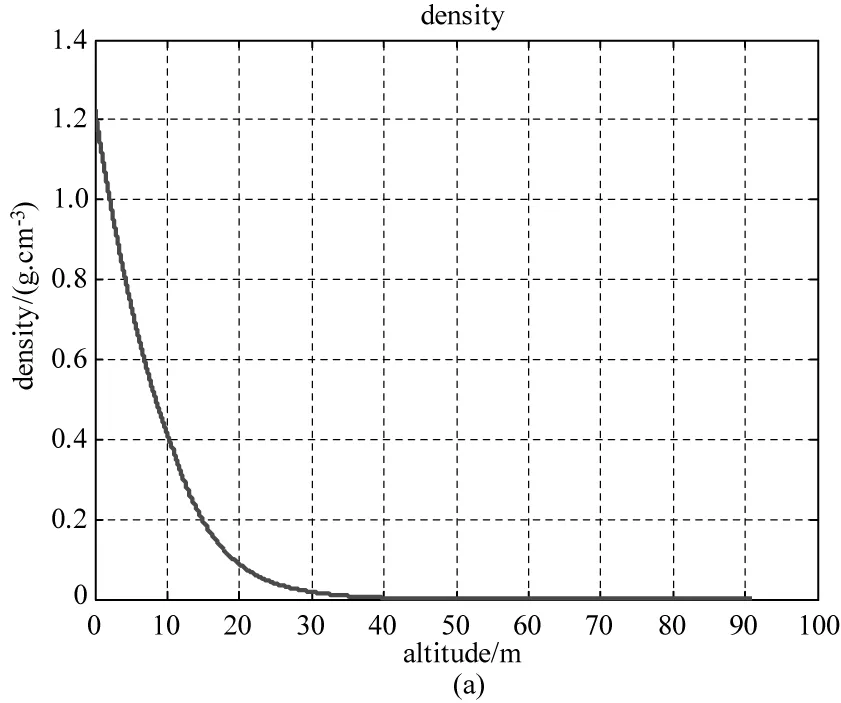
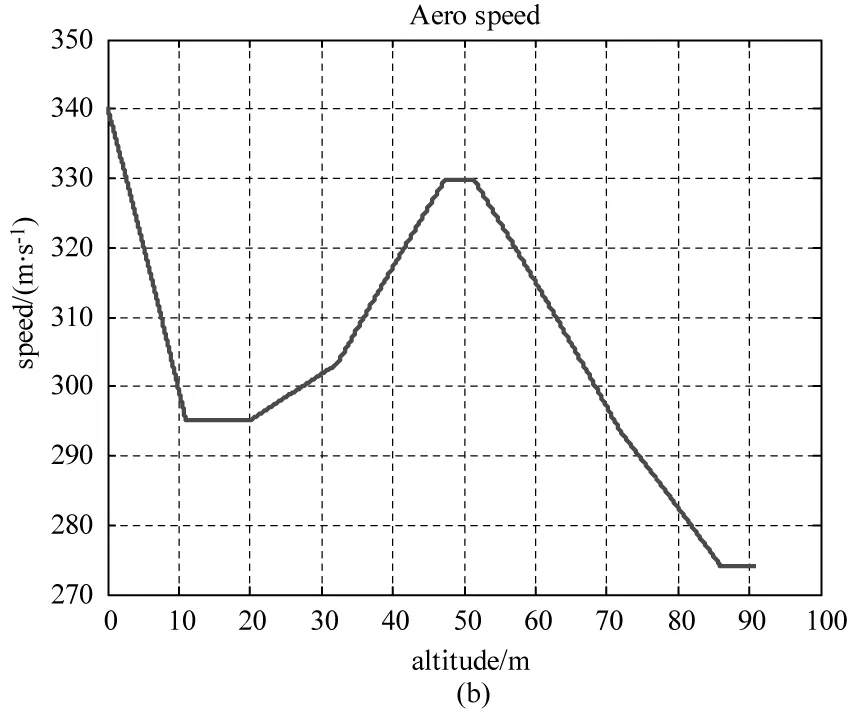
图1 标准大气参数计算结果

实际上,计算数值只能作为大气气象条件的一个参考值,现实中的气象条件随着时间的推移会不断变化。在需要精确的大气参数的场合,仍然需要以具体区域和条件下的细化模型或相关实时及场地测量数据为准。

3.2 基于高度系数矫正的驻点温度计算

基于实际工程计算经验,本文考虑采用大气密度作为该项系数(设定为a)的高度修正因子,并取海拔高度为19 km时该项系数(即a)取公式(2)中的工程经验值(即0.164)。此时公式(2)写为:

Ts=T0[1+a·Ma2]

(3)

系数a考虑高度修正,则高度为h处公式(3)中的系数a可以用如下修正公式:

(4)

式中,a0为海拔高度为19 km对应的系数(a0=0.164)；ρ0为海拔高度为19 km对应的大气密度；ρ为高度h处大气密度。

则高度h处的气动加热温度计算公式调整为:

(5)

式中,T0(h)为高度h处的大气温度；Ma(h)为高度h处飞行器飞行速度v对应当地声速的马赫数,其计算公式为:

(6)

3.3 目标黑体辐射计算

在对黑体进行辐射计算中,普朗克公式避免了维恩公式和瑞利-金斯公式无法计算特殊波段辐射的问题(尤其维恩公式,在长波段误差较大),能够适用于整个电磁波段[7]。因此,把高速飞行中的目标看作黑体,采用普朗克公式计算其驻点处的红外辐射,相应基本公式为:

(7)

其中,c1=2πhc2,c2=ch/k分别为第一、第二辐射常数。

4 典型计算结果分析

基于以上修正模型,针对典型高超声速飞行条件下的目标红外辐射情况进行仿真计算。仿真对象采用典型带控制翼的锥形体再入机动飞行器参数[11-12],质量设置为907 kg,气动参考面积0.35,其最大升力系数0.6,采用相关气动数据表格对升力系数和阻力系数进行拟合插值。为尽量涵盖目标飞行高度范围,经试验设置飞行条件为中高空小攻角再入模式:再入高度60 km,再入速度4600 m/s,再入弹道倾角-6°。应用经典动力学理论,得出对应目标运动弹道如图2所示。

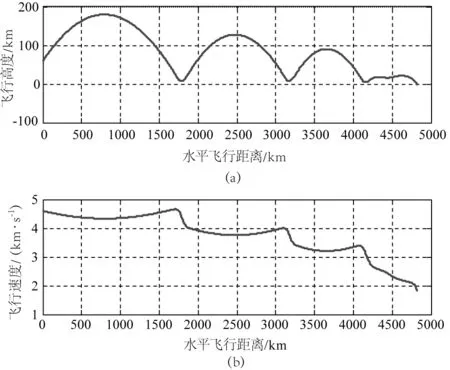
图2 目标运动弹道高度及速度参数

将目标运动参数注入提出的气动加热温度的修正计算模型,计算得出飞行器端点(驻点)的温度如图3所示。

基于黑体辐射模型,并结合当前主要红外探测装备工作波段及模式情况,可计算得出目标在典型红外波段的辐射曲线如图4所示。

对上述数据取半对数,得出结果如图5所示。

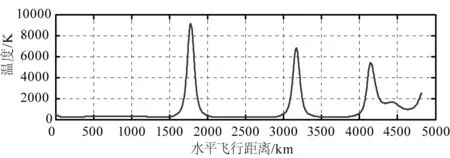
图3 目标弹头驻点温度

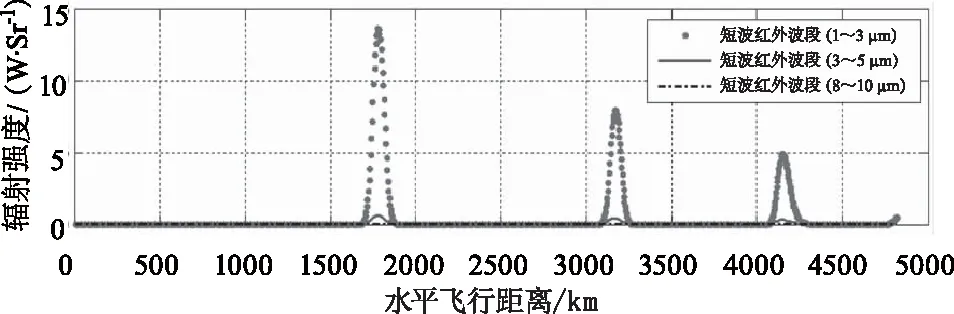
图4 目标弹头迎头方向的辐射强度计算结果

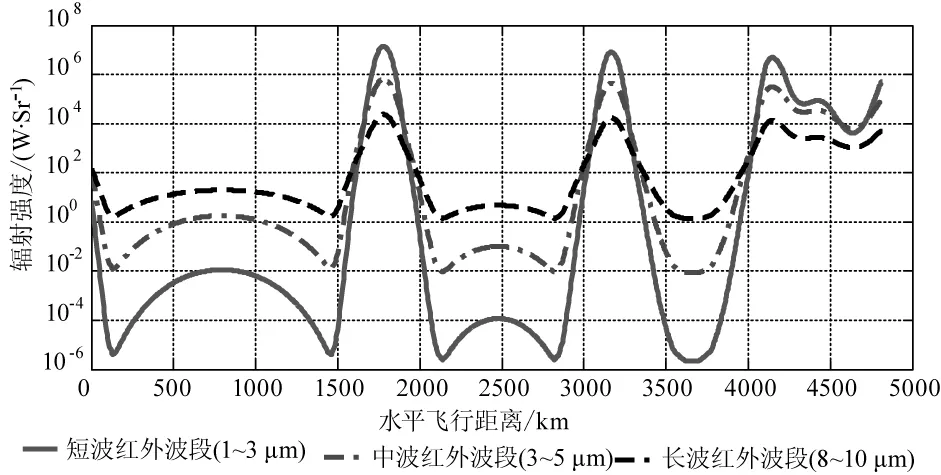
图5 目标弹头迎头方向的辐射强度(半对数)

综合以上各图分析,可以得出结论:

1)目标在做跳跃弹道飞行时,随高度降低其弹头温度急速升高,但其在高度上升后,弹头受气动加热产生的温度受速度和大气密度等参数的复合影响下降,其主要峰值的产生时机与弹道高度波谷(亦即速度峰值)基本重合。

2)在典型的中长短各个波段,总体辐射强度与温度呈正比关系,相应辐射强度峰值亦与气动加热温度及飞行速度紧密相关；长、中、短波段的辐射峰值可达104、106和107量级(单位W/Sr)。

3)目标速度越高,其短波辐射越强烈,而长波辐射相对较弱,反之,“低速”条件下则长波辐射更加强烈；三个波段辐射强度大体平衡的时机出现在多个弹道高度转换期间,其强度在102量级。

需指出的是,修正的公式主要侧重于气动加热的“外部”效应计算,但并未考虑弹头材质、热容及散热等自身“内部”特性。因而涉及到具体装备实验时,依然需进行细化考虑。

5 结 论

当前,对于高超声速条件下的热流计算及红外辐射计算问题,相关理论研究较多且大多数计算方法比较复杂,应用条件苛刻。在工程实现与测试验证方面,更缺少较为标准和有效的计算方法。而结合实际应用需求,可以基于相应工程计算经验,对某些关键参数进行合理的修正和调整,从而得出具有近似精度的计算结果,亦不失为一种较为实际的途径。