基于椭圆斑点序列图像估测清晰成像的方法

马 倩,朱兴龙,尹珺瑶

(扬州大学机械工程学院,江苏 扬州 225127)

1 引 言

单目视觉测量,因成本低廉、系统简洁所具备的特点,国内外学者做了大量的研究工作。文献[1]提出了一种在材料动态变形中对捕获的图像进行去模糊的方法,该方法与高斯方法和Lucy-理查森方法相比,它具有好的图像恢复效果；文献[2]针对光学畸变,提出了把光学畸变当作物体之间的几何变形,通过几何变换模型(GTM)建立光学系统,采用算法来估计GTM,消除制造和装配过程中引入的误差；文献[3]介绍了一种非接触式测量应力应变的方法,在承受压缩载荷的情况下,通过激光束反射在延性材料的横截面上图像的变化,通过图像处理分析这个区域的增加量值,得到了应力应变图；文献[4]提出了一种基于激光测量仪的单目视觉框架,通过曲线拟合确定拟合函数,修正镜头畸变；文献[5]提出了一种基于圆特征的单目视觉水下目标物3D距离估测方法,该方法解决了因光的折射造成图像失真的问题,应用解析几何解估测水下圆特征的方位和中心坐标；文献[6]在两种类型的美学判断中对序列效果进行量化,在连续判断过程中,观察到不同类型的偏差；文献[7]提出了一种在主成分分析(PCA)域中对降级的面部图像序列进行去噪的有效算法,该算法具有更好对面部图像的恢复和识别性能；文献[8]研究了场序(FS)成像背景下的运动补偿方法,解决了图像强度的已知方法和改进方法在图像变换和强度校正方法中的相邻图像通道之间的不一致的问题,获得了一组379种适用于FS数据流的运动估计方法；文献[9]提出了一种在Radon领域的Meteosat图像序列编码方法来解决不同成像器的遥感图像序列压缩方法的低呈现率问题。测试结果表明,该方法优于JPEG-LS标准的性能,可作为一般气象图像的预处理,特别适用于气象现象跟踪、分割等解压过程后的气象图像序列；文献[10]讨论了2D+X数据量上与机器学习有关的两个问题。对于数据条件问题,将二维空间卷积引入到基于一维希尔伯特的实例中,该方法对于卷积网络的信息可压缩性非常准确,并且提供了三种数据库；文献[11]针对复杂的环境条件,提出了一种基于多线索融合和卡尔曼滤波的红外小目标跟踪算法。实验结果证明,该算法可以有效提高跟踪的鲁棒性和准确性；文献[12]针对卷积神经网络(CNN)的深度学习模型中的目标检测问题,提出了一种新的易于学习的方法,通过无监督的时空分析来逐步改进图像序列中的对象检测；文献[13]针对单平台观测条件下目标运动特性反演问题,提出了基于序列图像的目标空间位置重建及运动参数估计模型和方法。采用反向追踪策略,根据追踪路径与目标发射面的交点,采用迭代估计,搜索最优发射面,确定目标空间位置；文献[14]提出了基于红外空域监测探测系统的视频运动模糊复原算法。该算法通过引入主、客观两套评价体系对使用的算法以及其他经典算法作对比,评估复原结果。实验结果表明:复原视频各帧的峰值信噪比和均方误差,均优于对比算法；文献[15]提出了一种基于3-D剪切波(3DST)和广义高斯模型的多模态医学序列图像融合方法来处理医学序列图像的局限性。通过实验对融合图像的主客观性能进行比较,结果表明所提算法可以获得更好的融合效果；文献[16]研究了一种仅使用单目相机对非合作目标进行远程相对运动估计的相对导航方法。该方法利用非线性系统的相对“局部弱可观测性”理论分析了单目序列图像的可观测性。 分析结果表明,仅依靠单目序列图像,完全估计远程非合作目标的相对运动；文献[17]针对口腔环境复杂性和牙齿拓扑结构多样性的问题,提出一种基于齿科序列图像的超分辨率重建算法,实验结果表明,这种算法提高了重建指标,具有较强的鲁棒性。

采用图像序列可以进行运动物体估测、测量和三维重建、非合作目标自主导航、多模态医学图像融合、模糊物体复原；利用卫星图像序列编码技术检测火灾区域及发生时间；通过序列图像的深度学习,可以实现动作识别、人脸识别、审美判断等。本文提出的一种基于序列斑点图像估测清晰成像位置的方法,即移动透镜在不同位置分别获取不同位置下的斑点图像,通过图像处理得到斑点图像中心坐标值,根据理论推导的解析模型,分成两段拟合,求取交点位置,该交点位置即为成像的最清晰位置。最后通过实验,将透镜调整至最佳位置并获取图像,通过边缘梯度检测和像素均值检测,验证了该位置就是清晰成像的最佳位置。

2 透镜成像模型

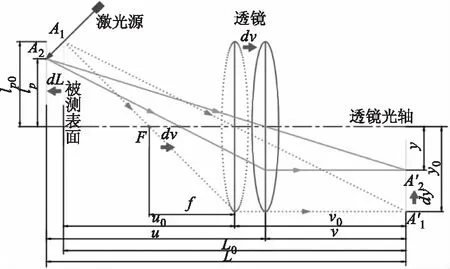
图1 透镜成像模型

由图1分析可知,假设初始位置服从透镜成像规律,则有:

(1)

若被测物体移动dL,则激光斑点在被测表面上移动后距离oo′为lp。

lp=lp0-dLtanα

(2)

由透镜成像公式可知:

(3)

由式(3)-式(1),可得深度信息差:

(4)

将式(2)代入式(4)得:

经整理得:

(ftanα+y)tanαdL2-(2flp0tanα-c0ytanα+lp0y)·

dL+flp02+fy2-c0lp0y=0

(5)

当测量系统安装完成后,式(5)中,lp0、α、f便固定下来,深度信息的变化dL仅与成像斑点中心坐标值y有关,如果知道成像光点中心坐标值y,那么深度信息的变化便可获得。

因此如何准确获取物体发生位移后的斑点中心坐标,是本文研究的关键问题。

3 透镜最佳位置搜索方法

3.1 搜索方法的理论分析

在测量范围内,通过直线伺服电机调整透镜的位置,运用相机记录透镜不同位置的斑点图像,形成斑点图像序列,该序列斑点图像将形成模糊→逐渐清晰→清晰→逐渐模糊→模糊的一个过程,表现为序列斑点图像的直径由最大→逐渐变小→逐渐变大→最大,如图2所示。

图2 斑点序列图像

这一过程中,清晰的图像从落在CCD面之前,逐渐落在CCD面上,然后落在CCD面之后。在记录的斑点图像序列中有可能没有服从透镜成像规律的最清晰图像,但是可以通过斑点图像的直径的变化与透镜移动的关系估测出服从透镜成像规律的透镜位置。如图3所示,当被测物体发生移动后,如果清晰图像成像在CCD面之前,实际成像在CCD面上的是模糊图像。模糊图像在y方向的界点由y1、y2、y3和y4的坐标表征。

图3 清晰图像成像在CCD面之前

在这种情况下,y3和y4被淹没在模糊图像中,因此界点由y1、y2表征,其表达式如式(6)和式(7)所示:

y1=(lp+r)(v0-f-dv)/f

(6)

y2=f(lp-r)/(u0-f+dL+dv)

(7)

由式(6)和式(7),计算斑点成像直径大小:

(8)

如果清晰图像成像在CCD面之后,实际成像在CCD面上的是模糊图像。

图4 清晰图像成像在CCD面之后

在这种情况下,y1和y2被淹没在模糊图像中,因此界点由y3和y4表征,其表达式如式(9)和式(10)所示:

y3=(lp-r)(v0-f-dv)/f

(9)

y4=f(lp+r)/(u0-f+dL+dv)

(10)

由式(9)和式(10),计算斑点图像直径大小:

(11)

当上述种情况下直径相等时,此时的dv即为凸镜位置的最佳值,该位置的成像一定落在CCD面上,即服从透镜成像规律,证明如下:

设初始位置的物距和像距分别为u0、v0,焦距为f,服从透镜成像规律,则有:

u0v0=f(u0+v0)

(12)

现在被测标靶移动dL,透镜移动dv,那么现在的物距和像距分别为u、v,则有:

u=u0+dL+dv

(13)

v=v0-dv

(14)

根据式(8)和式(11),当它们相等时,有:

dv2-(v0-u0-dL)dv-(v0-f)dL=0

(15)

解式(15)可得:

(16)

式(16)中,

Δ=(v0-u0-dL)2+4(v0-f)dL。

将式(16)分别代入式(13)和式(14),得:

(17)

(18)

由式(17)和式(18),可得:

(19)

将式(12)及Δ代入上式,得:

证毕。

3.2 算法实现

通过序列斑点图像,采用最小二乘椭圆拟合法可以获得斑点直径数据点集D(Di,dvi)和斑点中心数据点集C(yi,dvi)(i=1,…,I0),I0为序列斑点图像的个数。将斑点直径数据点集D(Di,dvi)分为两个子点集D(Di,dvi)(i=1,…,I0/2)和D2(Di,dvi)(i=I0/2,…,I0)。

针对子点集D(Di,dvi)(i=1,…,I0/2),采用式(8)和式(11)导出的解析式,采用罚函数法确定其参数,具体方法如下:

(20)

同时满足:

(21)

于是将式(20)、(21)转化为求以下罚函数的极值问题,即:

并规定:

这样可以获得:

(22)

同理可以获得子点集D2(Di,dvi)(i=I0/2,…,I0)对应的表达式如下:

(23)

求解式(22)和式(23),可得其交点,该交点的dv*值即为估测的透镜的最佳位置。

然后对斑点中心数据点集C(yi,dvi)(i=1,…,I0)进行拟合,所采用的方法同上,得到y=f(dv),将dv*代入,从而得到y*=f(dv*),y*就是通过序列斑点图像获取透镜最佳位置后,估测得到的清晰斑点图像的中心坐标。算法的流程图如图5所示。

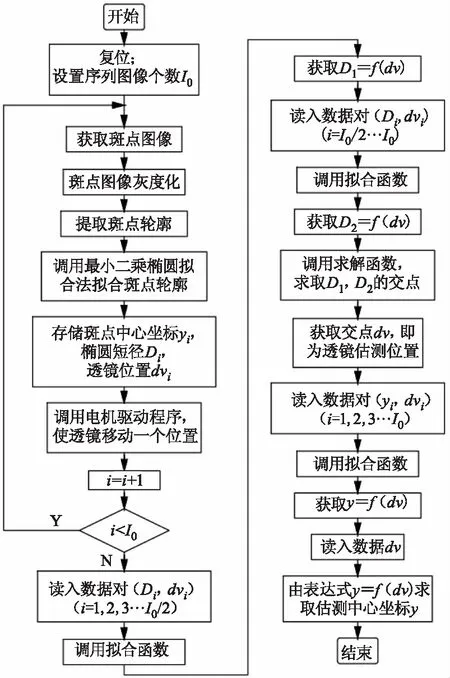
图5 拟合算法流程图

4 实 验

4.1 实验装置

实验装置由相机、光纤激光器、透镜、直线电机等组成,相机选用 BaumerTXG50c,分辨率为2480×1920,像素尺寸3.45 μm×3.45 μm镜头焦距25 mm,开发平台采用Vs2010 +OpenCv,如图6所示。

4.2 理论数据验证

为了验证以上所提方法的正确性和可行性,首先从理论数据入手,根据本文提出的测量系统,设u0=v0=2f,dL=5 mm,f=25 mm,r=5 mm,lp=25 mm,其解析解由式(2～27)得到,dv2+5dv-125=0,解之得dv*=8.9564 mm。根据光路图可得,清晰斑点图像中心坐标值y*=16.0436 mm。

图6 实验装置

下面通过设计的算法来进行估测,看看是否与解析求得的结果一致。首先通过式(8)和式(11),当dv从0变化到22 mm时(每次1 mm变化),获取斑点图像序列,得到斑点图像直径和斑点图像中心坐标值y,并记录在表1中。

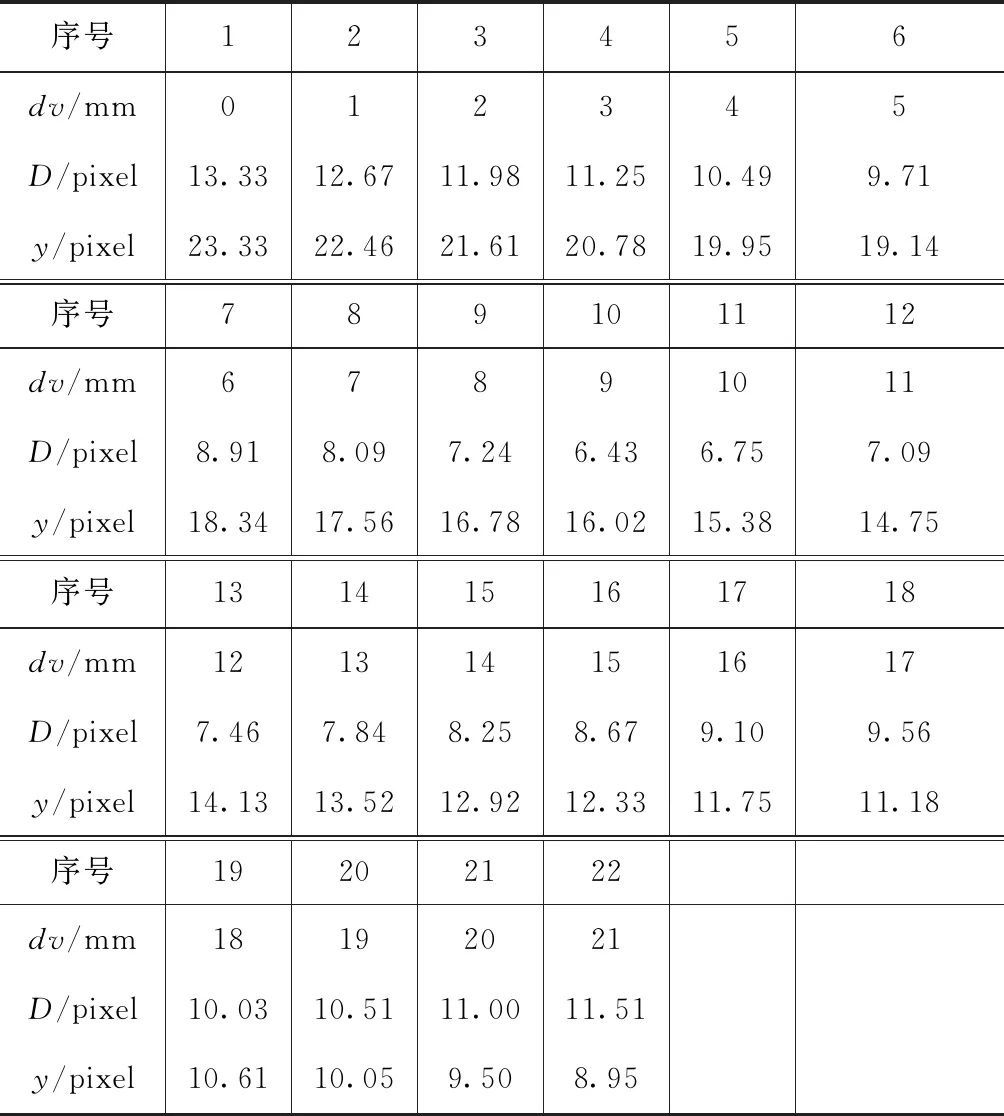
表1 理论斑点图像序列数据点集

根据表1的数据点集,得到斑点图像前段直径和后段直径的拟合函数如下:

(24)

(25)

它们的变化过程如图7所示,求解式(24)和(25),得dv*=8.9568 mm,而解析值为8.9564 mm,两者相差甚微,说明设计的基于斑点图像序列估测清晰成像位置算法从理论上是可行的和正确的。

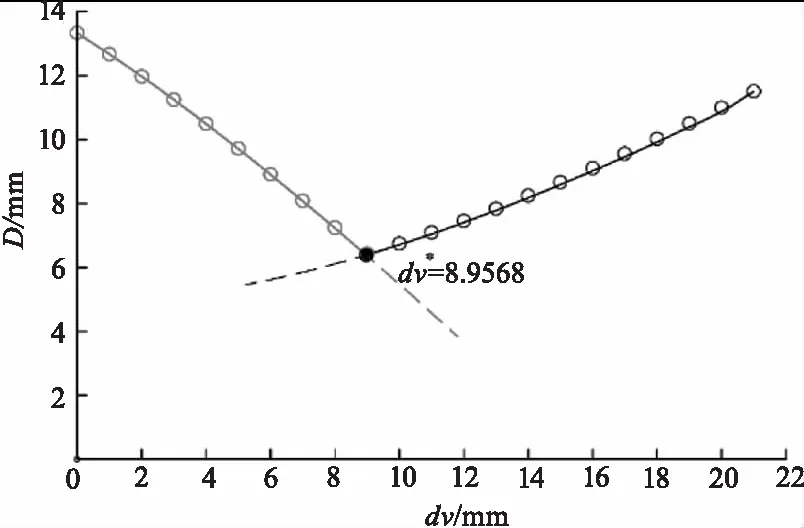
图7 斑点椭圆短径变化曲线

再从表1的数据点集,绘制斑点轮廓中心坐标值y随透镜位置变化的曲线如图8所示。

图8 斑点轮廓中心坐标值y变化曲线

从图8中可以看出,中心坐标值y与dv不符合线性关系,这里采用三次多项式函数拟合,其拟合的表达式如下:

y=23.396-0.938dv+0.016dv2-2e-4dv3

(26)

将dv*代入式(26),可得y=16.134 mm,而解析值为16.044 mm。两者相差0.09 mm,搜索方法所得到的解基本逼近解析解。

4.3 斑点图像序列估测实验

通过实验系统获取15幅序列斑点图像如图9所示,经灰度化处理后,通过轮廓提取,得到序列椭圆轮廓。从图7可以看出,序列斑点图像从模糊→逐渐清晰→清晰→逐渐模糊→模糊的过程,表现为序列斑点图像的短径由最大→逐渐变小→逐渐变大→最大,从序列斑点图像获取的数据点集见表2。

图9 序列斑点图像

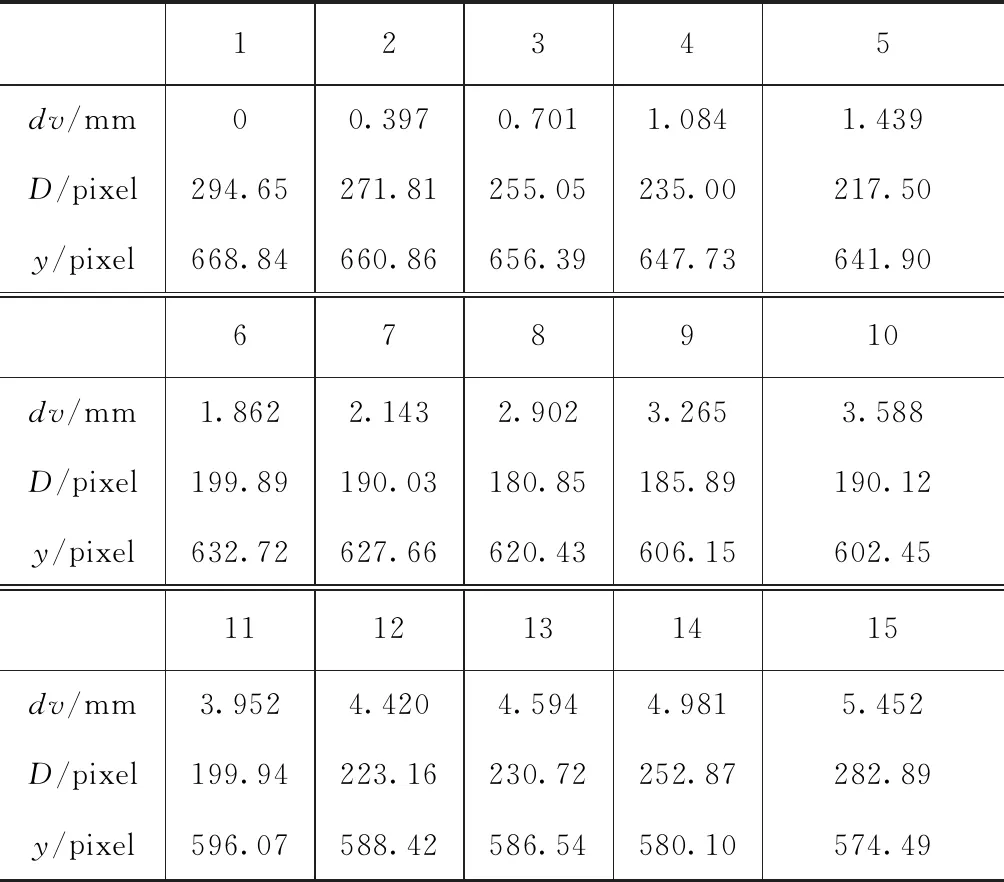
表2 序列斑点图像数据点集

根据表2的数据点集,得到椭圆短径前段和后段的拟合函数如下:

(27)

(28)

求解式(27)和(28),得dv*=2.950 mm。

在图10中,曲线①、④为表2中前半段数据的拟合曲线,,曲线②、③为表2中后半段数据的拟合曲线,两段拟合曲线在dv*=2.9503 mm处有交点,曲线③、④在透镜成像过程中实际上是不会产生的。

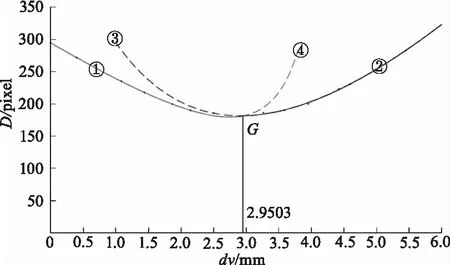
图10 斑点椭圆短径变化曲线

再从表2的数据点集,绘制斑点轮廓中心坐标值y随透镜位置变化的曲线如图11所示。从图11中可以看出,它们之间并不是线性关系,结合前面的理论数据拟合,这里仍采用三次多项式拟合,其表达式如下:

y=669.063-19.203dv-0.308dv2+0.119dv3

(29)

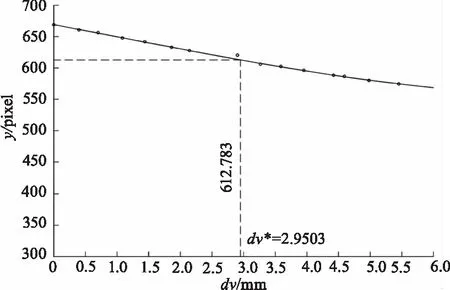
图11 斑点轮廓中心坐标值y变化曲线

将dv*代入式(29),可得y*=612.783pixel。这样将y*带入前面推导的公式(5),可以求得深度信息的变化。

4.4 清晰成像位置结果的实验验证

4.4.1 边缘梯度验证

为了验证上述估测结果的正确性,将透镜移至dv*,获取该位置的斑点图像,如图12所示。

采用图像处理获取该图像的边缘梯度值,并与15幅序列斑点图像的边缘梯度值进行比较,见表3。

图12 估测位置的斑点图像

表3 15幅斑点图像序列的边缘梯度均值

当dv*=2.9503 mm时,图像的梯度均值为130.8389。与表3中列出的梯度均值比较可以看出,该dv*=2.9503 mm位置的边缘梯度值最大,验证了该位置的斑点图像最清晰。

4.4.2 像素均值验证

采集的15幅斑点图像序列的像素均值,见表4。

表4 15幅斑点图像序列的像素均值

当dv*=2.9503 mm时,图12的像素均值为233.39 pixel。与表4中列出的像素均值比较可以看出,该透镜位置dv*=2.9503 mm时,估测图像的像素均值最大,验证了该位置的斑点图像最清晰,证明了通过斑点图像序列估测的清晰成像位置是服从透镜成像规律的,验证了基于斑点图像序列估测清晰成像位置的算法是可行的。

5 结 论

提出的一种基于斑点序列图像估测清晰成像位置的方法,通过图像处理获取斑点图像序列的椭圆短径数据。根据理论推导的解析模型,采用两段拟合,获取拟合函数,然后求取交点位置。通过理论证明,该交点位置即为估测的清晰图像位置。通过实验,计算了估测位置图像的梯度均值和像素均值,并与15幅斑点图像序列的梯度均值和像素均值相比较,估测位置的图像具有最大梯度均值和最大像素均值,验证了基于斑点图像序列估测清晰成像位置的算法是可行的。