均匀液滴喷射性能的实验研究

薛松龄，柴宝华，王泽鸣，朱锦新

均匀液滴喷射性能的实验研究

薛松龄，柴宝华，王泽鸣，朱锦新

（中国原子能科学研究院，北京 102413）

液滴式辐射器中液滴的喷射性能决定了液滴层中液滴的直径、间距、速度等参数，进而决定了整个液滴层的辐射散热性能。利用Rayleigh-Weber射流理论初步确定产生均匀液滴流的频率范围，完成了喷射实验装置的设计。通过实验研究了工质压力、扰动频率、喷孔的直径、喷孔长径比对均匀液滴流产生的影响。

均匀液滴；喷射；扰动频率

液滴式辐射器（Liquid Droplet Radiator）是一种新型的空间散热装置，其设计构想是由Mattick和Hertzberg[1]提出的。其工作原理是把热工质以细小液滴的形式向太空喷射，在行进过程中向空间辐射热量，工质液滴冷却后加以收集，由循环泵送回到换热器中继续进行工质循环。液滴式辐射器的散热是通过以亿计的小液滴组成的液滴层进行的，所以液滴式辐射器具有极大的散热面积。相同散热功率下，采用不同工质时液滴式辐射器的质量约为热管式辐射器质量的10%～20%[2]。在太阳能动力系统中如果使用液液滴式辐射器，整个动力系统的比质量与使用热管式辐射器时相比低约27%[3]。因此液滴式辐射器存在极大的质量优势。

液滴的喷射性能决定了液滴流中液滴的直径、间距、速度，这些参数又进一步决定了整个液滴层的辐射散热性能。因此许多研究者对液滴的喷射性能进行研究。White等人的研究发现喷射孔的形状并不影响形成均匀液滴的实验条件范围，形成均匀液滴流的实验条件的工作范围是由工质物性、扰动频率和液滴的速度等因素共同决定的[4]。日本的Tsuyoshi等在微重力条件下进行了单条液滴流喷射试验[5,6]，在微重力条件下验证了由质量守恒导出均匀液滴直径和间距的计算关系式。

国内针对液滴喷射性能也进行了很多研究，但主要的应用背景是面向喷墨打印、燃烧喷嘴以及压电润滑系统以及激光惯性约束聚变研究中的靶丸研制等。刘文巍等[7]为研究液滴喷雾燃烧，研制了单液滴发生装置，研究了不同电压、频率和喷口直径等条件下的液滴发生特性。魏胜等[8]采用液滴法制备空心玻璃微球，根据Rayleigh流体不稳定原理，确定了射流振荡波频率范围，分析了充电偏转过程，在不同的压力及孔径下，确定了最佳偏转振荡频率与射流初始速率和充电环长度的关系表达式。

本文围绕液滴式辐射器中液滴的喷射行为展开试验研究，分析了不同试验条件对均匀液滴流产生的影响。

1　液滴喷射原理

1990年Savart[9]对射流不稳定性和断裂机理进行了系统研究，发现射流表面存在着不同程度的扰动，这些扰动随时间逐渐增长，最终导致射流断裂而形成液滴。

Rayleigh[10-12]对射流不稳定性及其断裂机理进行了系统研究后提出，当扰动的增长速度最大时，为射流断裂的最优条件，并给出扰动增长率与无量纲波数的关系为：

Rayleigh射流理论中的射流的断裂条件与Plateau[13]提出的射流断裂条件一致。但Rayleigh理论只考虑了表面张力对射流断裂的作用，未考虑流体黏性和射流半径的影响。

Weber[14]对Rayleigh的扰动理论进行了完善和修正，考虑了液体的黏性和周围环境介质的密度，将射流不稳定方程修正为：

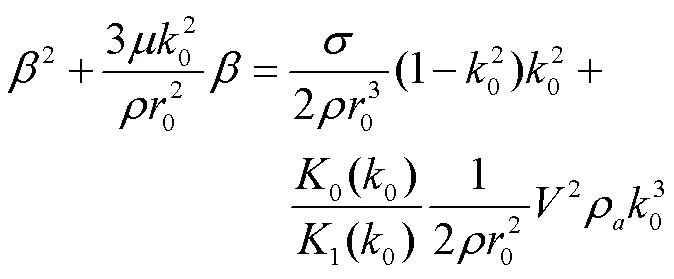
Weber在推导射流不稳定性方程的过程中仅考虑了环境介质密度的影响，而忽略了环境介质的黏度。

2　实验装置设计

实验采用的工质为DC704硅油，其工质特性如表1所示。液滴发生器的设计压力不高于0.5 MPa，液滴的设计直径范围为0.4～0.65 mm。

表1　DC704工质特性

图1　扰动增长率与无量纲波数的关系

振源系统主要由压电陶瓷、函数发生器和高压放大器等组成。

液滴流的拍摄和分析通过成像与分析系统完成，该系统的主要组成部件为高速摄像机、面光源、图像处理软件以及相关附件组成。高速像机型号为PCO.dimax.HD，相机的最小曝光时间为1ms，可连续拍摄液滴的形态。利用Camware图像处理软件进行图像处理。为了确定图像中液滴的尺寸，采用标尺进行对比测量，标尺的最小刻度为0.1 mm，精度为0.005 mm。

3　实验结果分析

试验过程中针对不同的工质压力、扰动频率、喷孔直径以及喷孔的长径比进行了喷射试验，并对结果进行了对比分析。液滴直径的实验数据是每种试验工况下9个液滴样本直径的平均值。

3.1　不同工质压力及扰动频率的影响

当喷孔的直径为0.2 mm，孔深为1 mm时，随着工质压力的增加，产生均匀液滴流的扰动频率也随之增加。

由图2可知当扰动频率在2.5 kHz时，射流断裂距离最短，液滴流呈现出相对均匀的液滴状态。

图2　0.2 MPa压力下不同扰动频率的实验结果

图3为0.3 MPa压力下不同扰动频率的试验结果。从图3中可以看到当扰动频率在4.5～5 kHz时，液滴流呈现出相对均匀的液滴状态。

图3　0.3 MPa压力下不同扰动频率的实验结果

随着工质压力的增加，产生均匀液滴的扰动频率也逐渐增加。产生的均匀液滴的直径逐渐减小，结果如表2所示。

表2　不同压力下0.2 mm喷孔的试验结果

3.2　不同喷孔直径的影响

喷孔直径分别为0.2 mm和0.3 mm（如表3所示），在不同工质压力下的喷射试验结果显示，产生均匀液滴流的扰动频率范围发生了明显地移动。

表3　不同压力下0.3 mm喷孔的试验结果

注：工质压力为0.2 MPa时，液滴的平均直径出现最大偏差为0.018 mm。

由表3和表2的结果对比可知，同样的工质压力条件下，孔径越小，喷射阻力越大，相应的射流喷射速度会减小，产生均匀液滴流的扰动频率也降低了。均匀液滴流中的液滴的直径也相应的减小。

3.3　不同喷孔长径比的影响

设定工质压力为0.2 MPa，喷孔直径为0.3 mm，孔深分别为0.5 mm、1 mm、2 mm、3 mm时进行喷射试验。

图4展示了当喷孔直径为0.3 mm，孔深为0.5 mm时不同扰动频率下的射流断裂情况。

图4　0.2 MPa压力下不同扰动频率的实验结果（孔径0.3 mm—孔深0.5 mm）

当孔深为0.5 mm时，随着扰动频率的增加，射流逐渐从非均匀液滴流到均匀液滴流再到非均匀液滴流的变化非常明显。扰动频率在2.5～3.5 kHz的频率范围内可以得到均匀的液滴流。

由图5可知，当孔深为1 mm时，产生均匀液滴流的扰动频率范围在4.5～6.5 kHz。由图6可知，当孔深为2 mm时，产生均匀液滴流的扰动频率范围在1～1.25 kHz。当孔深为3 mm时，扰动频率在0.5～2.25 kHz的范围内，未出现均匀液滴流，如图7所示。原因是喷孔的阻力过大，过低的流速导致无均匀液滴流的出现。

图5　0.2 MPa压力下不同扰动频率的实验结果（孔径0.3 mm—孔深1 mm）

图6　0.2 MPa压力下不同扰动频率的实验结果（孔径0.3 mm—孔深2 mm）

由于产生均匀液滴流的扰动频率随着射流速度的增加而增加，由上述实验结果可知，当孔深为1 mm时，射流速度最大。

当喷孔的长径比约为3时，通过喷孔的流量达到最大值。

图7　0.2 MPa压力下不同扰动频率的实验结果（孔径0.3 mm—孔深3 mm）

4　结论

通过喷射实验，得到如下结论：

（1）当工质射流的喷射速度变化时，产生均匀液滴的扰动频率也随之变化。当工质射流喷射速度增加时，产生均匀液滴流的扰动频率会随之升高。

（2）产生的均匀液滴的直径大小与喷孔直径有关，并随着频率的增加而减小。

（3）喷孔存在最优长径比，使得通过喷孔的工质流量最大。

［1］ Mattick A.T.，Hertzberg A. The Liquid Droplet Radiator -an Untralight weight Heat Rejection System for Efficient Energy Conversion in Space［J］．1982，9（3）：165-172.

［2］ Taussig R.T.，Mattick A.T. Droplet Radiator Systems for Spacecraft Thermal Control［J］．Journal of Spacecraft and Rockets，1986，23（1）：10-17.

［3］ Massardo A.F.，Tagliafico L.A.，Fossa M.，et al. Solar Space Power System Optimization with Ultralight Radiator［J］．Journal of Propulsion and Power，1997，13（4）：560-564.

［4］ White K A. Liquid Droplet Radiator Development Status［C］．22ndThermophysics Conference. 1987.

［5］ Tsuyoshi T.，Takuya K.，Kensuke W.，Kota N.，et al. Numerical and Experimental Studies on Circulation of Working Fluid in Liquid Droplet Radiator［J］．Acta Astronautica，2006，59：192-199.

［6］ Tsuyoshi T.，Takuya K.，Harunori N.，Isao K. Thermal Design of Liquid Droplet Radiator for Space Solar-Power System［J］．Journal of Spacecraft and Rockets. 2005，42（3）：493-499.

［7］ 刘文巍，黄云，李水清．适用于稳态蒸发和燃烧的定频率单液滴发生器的研究［J］．工程热物理学报，2013（08）：1570-1573.

［8］ 魏胜，漆小波，张占文，等．液滴发生器系统中流速及震荡频率的确定［J］．强激光与粒子束，2011，23（7）：1925-1928.

［9］ Plateau J.A.F.Statique Exp’erimentale et Th’eorique des Liquides Soumis aux Seules Forces Mol’eculaires［J］．Gauthier Villars：Pairs，1873，1（1）：2-10.

［10］ Rayleigh J W S. On the stability，or instability，of certain fluid motions［J］．Proceedings of the London Mathematical Society，1879，10（4）：57-70.

［11］ Rayleigh J W S. Further observations upon liquid jets，in continuation of those recorded in the Royal Society’s Proceedings for March and May［J］．Proceeding of the Royal Society of London，1882，34：130-145.

［12］ Keller J.B. Spatial instability of a jet［J］．Physics of Fluids，1973，16（12）：2052.

［13］ Rayleigh J W S. On the instability of jets［J］．Proceedings of the Royal Society of London，Mthematics，1878，10：4-12.

［14］ Yuen M. Non-linear capillary instability of a liquid jet［J］． Journal of Fluid Mechanics，1968，33（1）：151-163.

Experimental Study on Injection Performance of Uniform Droplets

XUE Songling，CHAI Baohua，WANG Zeming，ZHU Jinxin

（China Institute of Atomic Energy，Beijing 102413，China）

Diameter，space，velocity and other parameters of droplets，and then the heat radiation performance of the whole droplet layer，are determined by the droplet injection performance of liquid droplet radiator. Utilizing the Rayleigh-Weber jet theory，the frequency range at which uniform liquid droplet flow are output was preliminarily figured out，and the design of this experimental injection device. Through tests，the effects of working medium pressure，disturbance frequency，jet orifice diameter and length-diameter ratio on uniform droplet flow were verified.

Uniform droplet；Injection；Disturbance frequency

V41

A

0258-0918（2021）05-1042-05

2021-04-00

薛松龄（1981—），女，内蒙古赤峰人，高级工程师，硕士，现从事空间散热方面研究