基于ISO GUM的螺旋桨敞水试验不确定度分析方法研究
刘 伟,王文涛,孙立宪,毛镇界
(中国船舶科学研究中心,无锡 214082)
不确定度的概念最早由原美国标准局(NBS)在1963年提出,目前国际上通用的ISO GUM方法是国际标准化组织ISO于1995年正式发布的“测量不确定度表示指南”(Guide to the Expression of Uncertainty in Measurement).1998年至今,我国陆续修订发布了多稿国家计量技术规范,其评定方法及概念与GUM完全一致.最新版为JJF1059.1-2012[1].
在水动力性能模型试验方面,ITTC作为权威组织推荐了一些试验的不确定度分析导则,包括阻力、敞水、自航试验等.但是ITTC之前一直沿用AIAA (American Institute of Aeronautics and Astronautics)的不确定度分析标准,直到25届ITTC[2]才开始采用ISO-GUM的分析体系,提出了水动力试验不确定度分析导则[3],逐步确定了基于GUM法的阻力试验不确定度分析方法[4-8]. 但是ISO-GUM分析体系还未在ITTC普及,最新的关于敞水试验不确定度分析的相关研究[9]以及ITTC推荐规程Uncertainty Analysis, Example for Open Water Test[10]仍是以AIAA提出的“精密度误差(随机误差或者重复性)”和“极限误差(系统误差或固定误差)”为基础的,这种方法和当今国际主流以及国内计量标准体系采用的ISO GUM(1995年)中的不确定度评定方法(A类不确定度和B类不确定度)是不一致的,在水动力试验计量校准等方面并不适用.
1 ISO GUM 方法
国家计量规范JJF1059.1-2012[11]以及国际标准ISO/IEC Guide 98-3:2008[12]关于测量不确定度表示指南的缩写为GUM,称其为GUM法.
1.1 评定步骤
GUM法评定测量不确定度的步骤:① 明确被测量的定义、测量方法、测量条件等;② 建立被测量的测量模型,分析对测量结果有明显影响的不确定度来源;③ 评定各输入量的标准不确定度;④ 计算合成标准不确定度;⑤ 确定扩展不确定度;⑥ 报告测量结果.
1.2 输入量的标准不确定度评定
(1) A类评定
标准不确定度的A类评定,是指对规定测量条件下测得的量值,用统计分析的方法进行测量不确定度分量的评定,其中规定测量条件包括重复性测量条件、期间精密度测量条件或复现性测量条件.
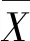
(1)
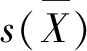
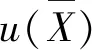
(2) B类评定
标准不确定度的B类评定,是借助于一切可利用的有关信息进行科学判断得到估计的标准偏差.通常是根据有关信息或经验,判断被测量的可能值区间[x-a,x+a],假设被测量可能值在该区间内的概率分布,根据概率分布和要求的概率p确定k的值,则B类评定的标准不确定度u(x)的计算为:
(2)
式中:a为被测量可能值区间的半宽度;k为置信因子或包含因子,可根据概率论获得.
2 螺旋桨敞水试验不确定度源
2.1 敞水试验原理
螺旋桨模型敞水试验典型方法如图1,采用定转速变车速的方法,测量螺旋桨进速V、螺旋桨的转速n、推力T和扭矩Q以及带桨榖状态下的阻力.通过桨榖阻力修正得到由螺旋桨桨叶发出的实际推力.敞水试验的测量值通过无因次化处理可以得到进速系数J、推力系数KT和扭矩系数KQ.
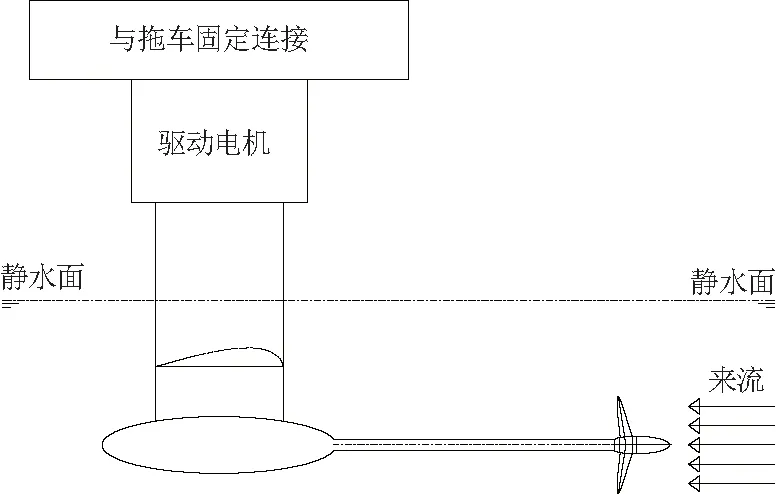
图1 模型敞水试验装置Fig.1 Model open water test device
2.2 试验不确定度源
根据敞水试验的原理和测试流程,可梳理得到影响敞水试验的主要不确定度源如图2,包括模型几何、试验安装、仪器校准、测量重复性4个方面.

图2 桨模敞水试验不确定度源Fig.2 Uncertainty sources of propelleropen water model test
(1) 模型几何
桨模几何因素方面通常包括加工用三维模型建模精度、桨模加工精度以及存放过程中变形引入的不确定度.
(2) 试验安装
轴系角度:指敞水试验过程中敞水动力仪轴线与拖车前进方向的一致性,两者之间的夹角会导致桨模迎流角变化,引入推扭力测量不确定度.
桨模浸深:指桨模敞水试验时,桨轴线距离水面的深度,试验前会根据桨模直径进行估算,确定合适的深度,可将该不确定源影响降到较低水平.
导流与顺流:指敞水试验时导流帽和顺流段的尺度对流场的影响,进而影响桨模敞水试验测量.
(3) 仪器校准
车速、水温计、转速编码器、敞水动力仪等测量装置在校准过程中的偏差会引入进速、水温、转速和推力扭矩测量的不确定度,进而传递到推力和扭矩测量不确定度中.
(4) 测量重复性
通过设计重复试验,在不同航次下记录车速、水温、推力、扭矩、桨股阻力,不同航次间的偏差即为重复测量的不确定度.
3 螺旋桨敞水试验不确定度分析方法
3.1 测量模型
在螺旋桨模型敞水试验满足临界雷诺数的条件下,表征螺旋桨的敞水特性的推力和扭矩系数曲线通常趋于恒定,仅与进速系数相关.在螺旋桨敞水试验中,由于池水密度、转速、直径以及进速测量的不确定度会传递到推力和扭矩测量结果的不确定度中,因此可建立推力和扭矩测量模型为:
(3)
(4)
式中:TP和QP分别为试验测得的螺旋桨推力(桨毂阻力修正后)和扭矩;DP为螺旋桨直径;V,n分别为螺旋桨进速和转速;KT和KQ分别为螺旋桨敞水测得推力和扭矩系数.
根据前期研究,桨毂阻力占总推力的比例只有1%左右,且桨毂阻力的测量不确定度较小,因此可忽略由于桨毂阻力测量引入的螺旋桨推力测量不确定度.
3.2 灵敏系数
根据螺旋桨推力和扭矩测量模型可以看出,影响螺旋桨敞水试验测量的输入量主要有螺旋桨直径、螺旋桨转速、螺旋桨进速、池水密度、敞水动力仪校准、螺旋桨推力和扭矩测量重复性.
(1) 几何因素引入的不确定度
桨模几何不确定度主要是型值误差,包括螺距、叶厚以及螺旋桨直径的不确定度,考虑到桨模采用数控加工成型,加工精度较高,且螺旋桨螺距及叶厚等因素的微小差别难以通过灵敏系数表示,因此只考虑螺旋桨直径的不确定度对推力测量的不确定度影响.螺旋桨直径的不确定度对推力测量的不确定度影响主要反映在直径和进速的影响:
(5)
因此螺旋桨模型直径引入的推力测量不确定度灵敏系数可表示为:
(6)
(2) 池水温度引入的不确定度
池水温度的不确定度主要影响池水密度ρ和粘度ν,其中池水粘度主要影响螺旋桨敞水试验时的雷诺数,而通常的敞水试验均满足临界雷诺数要求,此时由粘度的微小差异引起的雷诺数差异几乎对螺旋桨敞水特性无影响.因此池水温度的不确定度分量只考虑池水密度的不确定度分量.
(7)
因此池水密度引入的推力测量不确定度灵敏系数为1.
(3) 螺旋桨转速引入的不确定度
螺旋桨转速的不确定度对推力测量的不确定度影响主要反映在转速和进速:
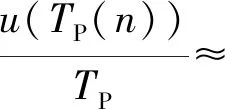
(8)
因此,由螺旋桨模型转速引入的推力测量不确定度灵敏系数可表示为:
(9)
(4) 拖车速度引入的不确定度
螺旋桨敞水试验时拖车速度的不确定度会传递到进速系数中,进而引入推力测量的不确定度:
(10)
因此,由拖车速度引入的推力测量不确定度灵敏系数为:
(11)
(5) 推力校准与测量重复性
显然,推力校准和重复测量分散性引入的不确定度灵敏系数为1.同理可以推导得到扭矩测量各输入量的灵敏系数,如表1.

表1 敞水试验不确定度输入量灵敏系数Table 1 Sensitivity coefficient of uncertaintyinput in open water test
对于常规水面船螺旋桨,敞水特性表中KT(J)和KQ(J)可表达采用4次多项式,如KT(J)可表示为:
KT(J)=AJ4+BJ3+CJ2+DJ+E
(12)
则K′T(J)可表示为:
K′T(J)=4AJ3+3BJ2+2CJ+D
(13)
3.3 合成与扩展不确定度
考虑到影响螺旋桨敞水推力测量的不确定度的各分量不相关,因此推力和扭矩测量的相对合成标准不确定度可按下式计算:
(14)
扩展不确定度可表示为:
U′p(y)=kpu′c(y)
(15)
其中,kp为包含概率为p时的包含因子.当输出量的概率分布接近正态分布时,置信度95%对应的包含因子kp可根据计量规范取为2[1].
4 实例分析
4.1 试验
以一个直径250 mm螺旋桨标准模型作为研究对象,为了保证桨模的加工质量,桨模及配件均采用镍铝青铜加工.螺旋桨主尺度和参数如表2.
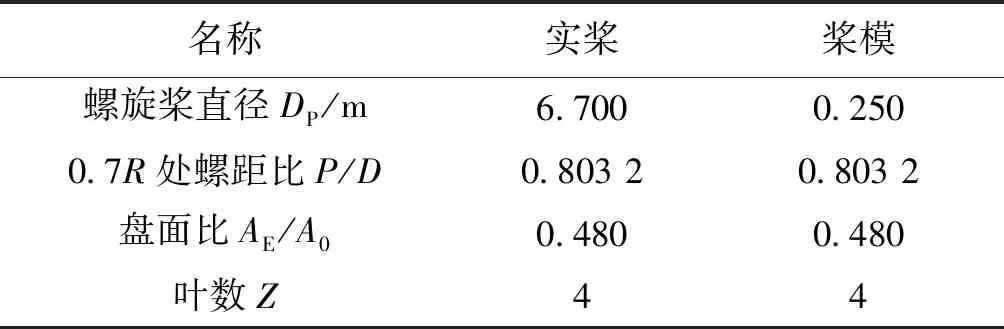
表2 螺旋桨主尺度和参数Table 2 Main dimensions and parameters of propeller
试验桨模转速取为18 r/s,此时螺旋桨0.7R处对应的特征雷诺数约为5.6×105,满足临界雷诺数要求.在同一天内开展了该桨模6个不同进速(表3)下的10次敞水重复测量试验,试验过程中采用相同的等水时间,每次试验前采集零点并记录水温,保证测试系统,测试人员、测试工况的完全一致,符合重复性测量条件.

表3 桨模敞水试验速度Table 3 Ropeller model open water test speed
4.2 测量不确定度分析
4.2.1 不确定度分量
(1) 桨模直径
试验模型采用镍铝青铜,通过高精度数控加工中心加工成型,针对加工完成的桨模进行了详细的型值检验.综合考虑桨模型值检测结果和切削机的定位精度,桨模的直径加工精度取为0.01 mm,考虑到桨模直径在该精度范围的任意处可能性相同,因此可假设其不确定度满足均匀分布,则桨模直径的标准不确定度为:
(16)
相对标准不确定度为:
(17)
(2) 池水密度
试验过程中在水池3个不同位置分别安装了水温计并进行了记录,不同位置处水温均为26.1℃,因此水池温度分布不均引入的水温不确定度可忽略.水温计出厂标示的精度为0.5℃,满足正态分布,则水温测量的不确定度为:
(18)
试验温度为26.1℃,对应的池水密度为996.759 7 kg/m3,此时当水温上下偏差0.2℃时对应的密度分别为996.812 9 kg/m3和996.706 2 kg/m3.则池水密度的相对标准不确定度可取为:
(19)
(3) 螺旋桨转速
敞水动力仪转速反馈的转速精度为0.2%,基于转速编码器的出厂说明,其不确定度满足正态分布,则螺旋桨转速测量的相对标准不确定度为:
(20)
(4) 车速
拖车速度V的分辨率为0.001 m/s,考虑到车速在该精度范围的任意处可能性相同,因此可假设其不确定度满足均匀分布,则拖车速度的标准不确定度为:
(21)
对应不同车速下的相对标准不确定度如表4.

表4 车速的相对标准不确定度Table 4 Relative standard uncertainty of carriage speed
(5) 仪器校准
敞水试验前对敞水动力仪进行了静校,利用标准砝码进行了3次重复加载,根据式(22,23)将校验的推力和扭矩系数乘以电压值Volt可以得到不同负载下的推力T的扭矩值Q.根据式(24)可以求得推力和扭矩的校准不确定度SEE分别为0.20 N、0.010 N·m.[12]
T=-20.706 2×Volt
(22)
Q=13.316 6×Volt
(23)
(24)
(6) 重复试验
针对重复测量结果,首先需要将推力、扭矩换算到平均水温状态,考虑到试验中1天内10次重复测量的水温并无差异,因此无需进行水温修正.根据10次敞水重复试验结果,采用贝塞尔公式可得到螺旋桨推力、扭矩测量重复性的标准不确定度如表5.可以看出不同进速下螺旋桨模型推力和扭矩的测量重复性标准不确定度水平相当.
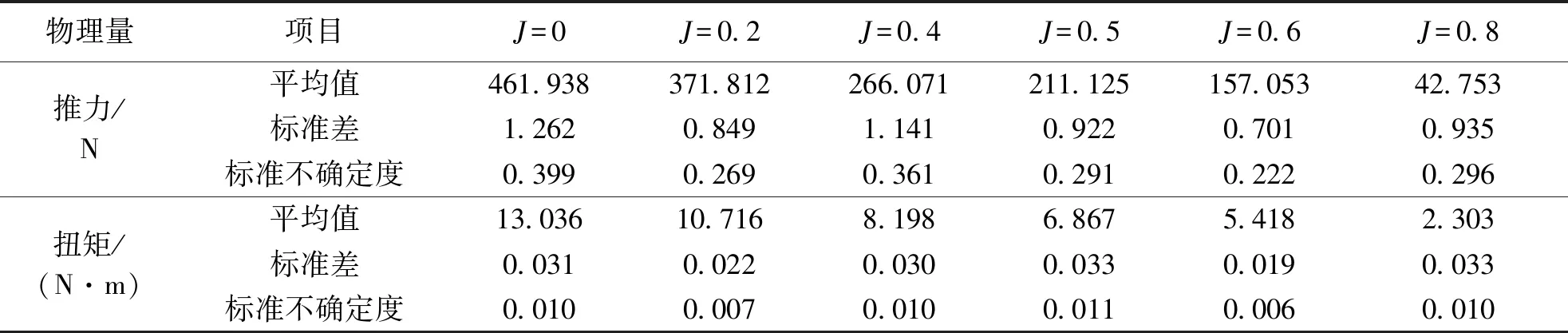
表5 桨模推力与扭矩测量重复性标准不确定度Table 5 Standard uncertainty of repeatability of propeller model thrust and torque measurement
4.2.2 不确定度概算
利用上一节的敞水不确定度分析方法,可以计算得到不同输入量的灵敏系数与不确定度分量,通过合成和扩展得到95%置信度下的螺旋桨敞水试验推力和扭矩测量的不确定度,表6、7给出了6个不同进速下的不确定度概算.
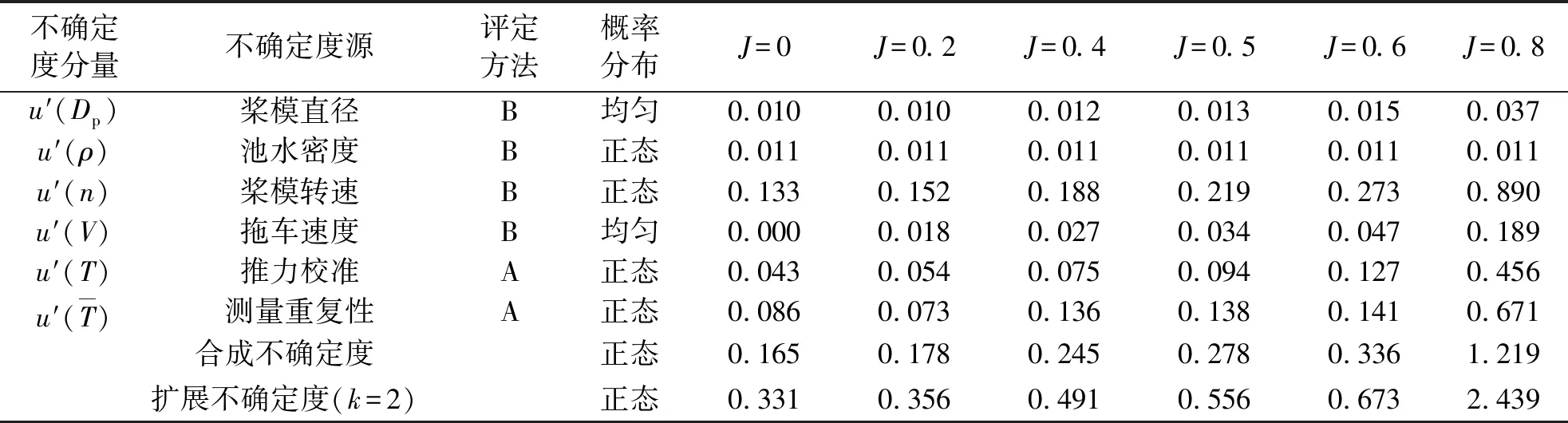
表6 模型敞水推力测量不确定度概算Table 6 Uncertainty estimation of thrust measurement in open water test %
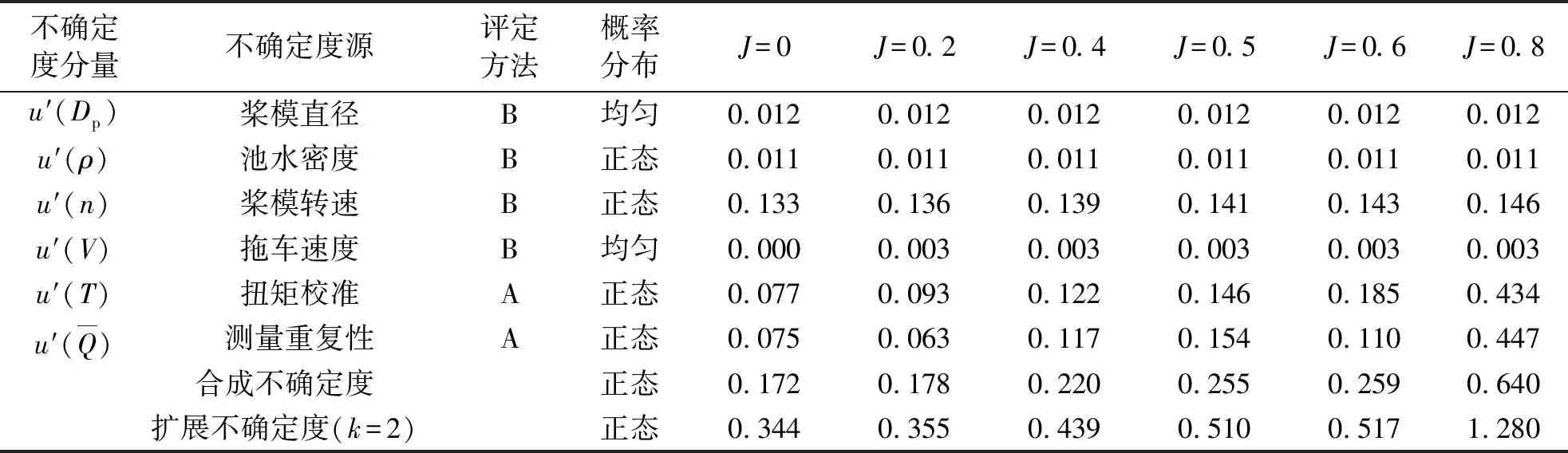
表7 模型敞水扭矩测量不确定度概算Table 7 Uncertainty estimation of torque measurement in open water test %
4.2.3 不确定度报告
根据10次重复测量结果可以获得敞水推力和扭矩的测量重复性偏差分布,通过概算可以分别得到单次测量结果以及10次重复测量平均值的不确定度水平,如表8.其中单次测量结果的不确定度水平由10次重复测量结果的标准差表示. 对比结果表明开展重复测量可以有效降低敞水试验的不确定度.

表8 螺旋桨模型敞水试验不确定度(95%置信度)Table 8 Uncertainty of propeller model open water test (95% confidence)
5 蒙特卡洛法验证
国际计量局(BIPM)计量学指南委员会(JCGM)以及中国计量标准中在ISO框架下给出了GUM法和蒙特卡洛法两种测量不确定度分析方法,其中GUM法适合测量模型和传递函数清晰简单的测量不确定度分析,而蒙特卡洛(MCM)法适合于测量模型复杂、计算模型的偏导困难等情形.
MCM是一种通过重复采样实现分布传播的数值方法[13-15],即利用对概率分布进行随机抽样而进行分布传播的方法.与GUM法利用线性化模型传播不确定度的方法不同,MCM通过对输入量进行离散抽样,由测量模型传播输入量的分布,计算获得输出量的离散采样值,进而由输出量的离散分布数值直接获取输出量的最佳估计值、标准不确定度和约定包含概率的包含区间.因此MCM法也被推荐为GUM法的适用性验证方法.
基于MCM法针对本实例中的敞水试验不确定度进行了分析,采用与GUM法一致的测量模型与概率分布,得到了95%置信度下的平均值、标准差与包含区间.根据MCM验证方法,当GUM法与MCM的包含区间左右端点偏差小于数值容差时,则GUM法可通过验证.表9、10中分别列举了两种方法推力和扭矩测量不确定度分析结果对比,可以看出在本实例中,数值容差为0.005,不同进速下推力和扭矩的不确定度分析结果都能通过MCM验证.

表9 GUM法与MCM法推力不确定度分析结果对比Table 9 Comparison of thrust uncertainty analysis results between GUM and MCM method
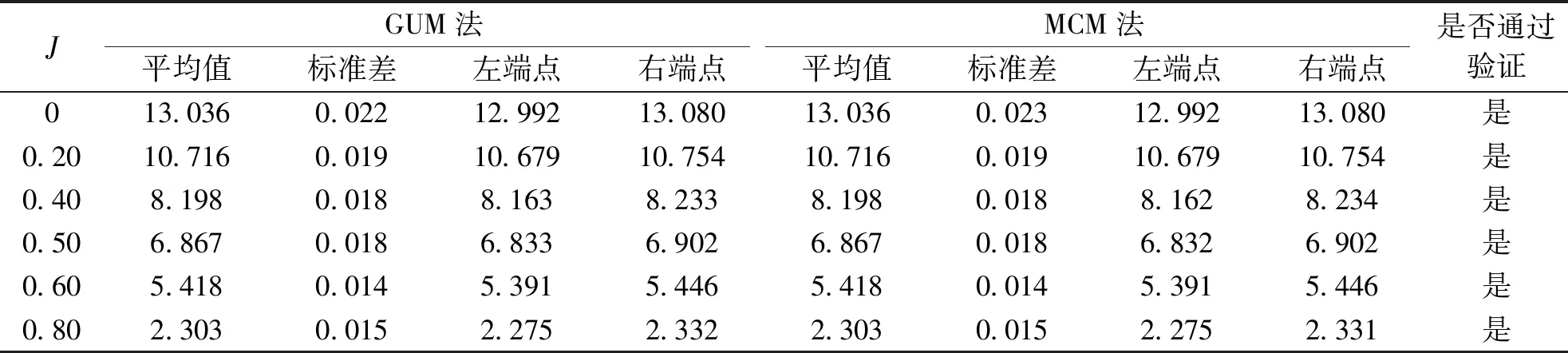
表10 GUM法与MCM法扭矩不确定度分析结果对比Table 10 Comparison of torque uncertainty analysis results between GUM and MCM method
6 结论
(1) 在对主要不确定度源采取了严格的控制措施的前提下,影响敞水试验不确定度的主要因素为仪器校准和重复试验偏差,模型几何、池水温度、桨模转速和拖车速度等不确定度分量可忽略.
(2) 在螺旋桨敞水试验中,开展重复试验可以有效降低测量不确定度,对于文中选用的螺旋桨模型和测量系统,进数系数J=0.5时,开展10次重复试验获得敞水推力和扭矩均值的不确定度相较单次测量分别下降了44%和52%.
(3) 在单次重复测量中,测量重复性的不确定度分量为主要因素,随着测量次数的增加,当重复测量的不确定度分量减小到不占主要影响因素时,降低不确定度则需要考虑更换精度更高的测量设备等其他措施.
(4) 文中提出的基于GUM的敞水试验不确定度分析方法能够通过蒙特卡洛法的对比验证,可作为敞水试验不确定度分析的普适性方法.
参考文献(References)
[1] 中华人民共和国国家质量监督检验检疫总局. 测量不确定度评定与表示[S]∥中华人民共和国计量校准规范JJF 1059.1-2012,北京:中国标准出版社,2012.
[2] 吴宝山. 25thITTC不确定度分析委员会工作简要回顾[C]∥中国造船工程学会.2008年船舶水动力学学术会议论文集.杭州:[s.n.], 2008:353-358.
[3] ITTC.Recommended Procedures and Guidelines. Guide to the Expression of Uncertainty in Experimental Hydrodynamics[S].[S.l.]: ITTC,Recommended Procedures and Guidelines,2014.
[4] ITTC.Recommended Procedures and Guidelines. General Guideline for Uncertainty Analysis in Resistance Tests[S]. [S.l.]: ITTC,Recommended Procedures and Guidelines,2014.
[5] 吴宝山. 船模水动力学试验中几何参数的不确定度分析研究[J]. 船舶力学, 2007(3): 363-372. DOI: 10.3969/j. issn. 1007-7294.2007.03.006.
WU Baoshan. On geometric parameters in uncertainty analysis of measurement in ship model test[J]. Journal of Ship Mechanics, 2007(3): 363-372. DOI: 10.3969/j. issn. 1007-7294.2007.03.006.(in Chinese)
[6] 施奇,杨大明,尹赟凯. 拖曳水池船模阻力试验不确定度分析[J]. 江苏科技大学学报(自然科学版), 2010,24(5): 428-433. DOI: 10.3969/j. issn. 1673-4807. 201005428.
SHI Qi, YANG Daming, YIN Yunkai. Uncertainty analysis of ship model resistance test in towing tank[J]. Journal of Jiangsu University of Science and Technology. 2010,24(5): 428-433. DOI: 10.3969/j. issn. 1673-4807. 201005428. (in Chinese)
[7] 金仲佳, 刘胜, 吴宝山, 等. 拖曳水池船模阻力校准技术研究[J]. 中国造船, 2015,(3): 162-171. DOI: 10.3969/j. issn. 1000-4882. 2015.03.018.
JIN Zhongjia, LIU Sheng, WU Baoshan, et al. Research on calibration technology of ship model resistance in towing tank[J]. Shipbuilding of China, 2015,(3): 162-171. DOI:10.3969/j.issn.1000-4882. 2015.03.018. (in Chinese)
[8] 周广利,黄德波,李凤来.船模拖曳阻力试验的不确定度分析[J]. 哈尔滨工程大学学报, 2006,27(3): 377-381,390. DOI:10.3969/j.issn.1006-7043.2006.03.013.
ZHOU Guangli, HUANG Debo, LI Fenglai. Uncertainty analysis of ship model towing resistance test[J]. Journal of Harbin Engineering University, 2006,27(3): 377-381. DOI: 10.3969/j. issn. 1006-7043. 2006.03.013. (in Chinese)
[9] 何术龙,陈玮琪,郭圣汉,等. 拖曳水池敞水试验的测量不确定度分析[C]∥中国造船工程学会. 2004年船舶水动力学学术会议论文集,武汉:[s.n.],2004:87-96.
[10] ITTC.Recommended Procedures and Guidelines. Uncertainty Analysis Example for Open Water Test[S]. [S.l.]: ITTC,Recommended Procedures and Guidelines,2014.
[11] ISO/IEC GUIDE 98-3. Uncertainty of measurement Part3: Guide to the expression of uncertainty in measurement (Supplement 1:Propagation of distributions using a Monte Carlo method)[S]. Switzerland:[s.n.],2008.
[12] ITTC.Recommended Procedures and Guidelines. Uncertainty Analysis, Instrument Calibration[S]. [S.l.]: ITTC,Recommended Procedures and Guidelines,2017.
[13] 牛恒,牛娜.自适应蒙特卡洛法在测量不确定度评定中的应用[J].宁夏工程技术, 2019,18(1):72-75,85. DOI:10.3969/j.issn.1671-7244.2019.01.015.
NIU Heng, NIU Na. Application of adaptive Monte-Carlo method in uncertainty measurement[J]. Ningxia Engineering Technology. 2019,18(1): 72-75,85. DOI: 10.3969/j.issn.1671-7244.2019.01.015. (in Chinese)
[14] 魏明明.蒙特卡洛法与GUM评定测量不确定度对比分析[J].电子测量与仪器学报, 2018,32(11):17-25. DOI:10.13382/j.jemi.2018.11.003.
WEI Mingming. Comparative analysis of measurement uncertainty evaluation with Monte Carlo method and GUM[J]. Journal of Electronic Measurement and Instrumentation, 2018,32(11):17-25. DOI:10.13382/j.jemi.2018.11.003. (in Chinese)
[15] 张婉洁,赵轶.蒙特卡洛法测量不确定度评定中测量模型的建立[J].计量与测试技术, 2017,44(9):56-57,59. DOI:10.15988/j.cnki.1004-6941.2017.09.024.
ZHANG Wanjie, ZHAO Yi. Discussion on the establishment of measurement model in the uncertainty evaluation by the Monte Carlo method[J]. Metrology & Measurement Technique,2017,44(9):56-57,59. DOI:10.15988/j.cnki.1004-6941.2017.09.024. (in Chinese)

