煤矿工人心律失常检测的LSTM-CNN T 波识别方法

史健婷， 孙 骏

(黑龙江科技大学 计算机与信息工程学院， 哈尔滨 150022)

0 引 言

煤矿产业是我国国民经济支柱产业之一。据估计，我国煤矿井下作业人员人数超过600万[1]。这些工人在从事劳动生产过程中，长期处于粉尘、噪声、局部振动和高温高湿等环境中[2]。长期结果会导致尘源性肺气肿，使肺血管阻力增加，产生肺动脉高压，进而引起心肌收缩抑制与心室复极延缓、复极化不均，从而导致心律失常的发生[3]。目前，国内外很重视对煤矿工人心律失常方面的研究，在心律失常的检测诊断中，心电图起着重要的作用。心电图反映了心脏兴奋的产生、传导和恢复过程中的生物电变化，可以检测并比较煤矿工人在不同生产环境下的各种心率指标[4]。在心电图的分析中，T波代表心室复极，T波显著抬高、T波倒置是诊断煤矿工人有无心肌缺血、心肌梗死、电解质紊乱的重要指标。因此，T波识别是检测心律失常的一种有效手段，然而T波噪声较大，形态多样，往往识别的效果不理想。笔者基于长短时记忆网络(Long short-term memory，LSTM)和卷积神经网络(Convolutional neural networks，CNN)结合的模型，提出一种经过鲸鱼优化算法(Whale optimization algorithm，WOA)优化的T波识别方法，以提升T波识别的准确率。

1 数据预处理

采用卡尔曼滤波对心电信号进行数据预处理去噪。卡尔曼滤波采用状态空间方法描述系统，算法采用递推形式，数据存储量少，不仅可以处理平稳随机过程，也可以处理多维和非平稳随机过程[5]。卡尔曼滤波器递推迭代过程分为预测和更新两步递推算法主要有三步。

步骤1计算预测部分

(1)

(2)

式中：A——状态转移矩阵；

B——控制矩阵；

L——采样点的长度；

P——状态估计值的方差；

Q——系统噪声方差矩阵。

步骤2计算更新部分。根据式(2)可得卡尔曼增益为

(3)

式中：C——系数矩阵；

R——观测噪声方差矩阵。

由式(1)可化简得估计值为

式中,y——观测值。

步骤3更新真实值与估计值的协方差矩阵：

式中,I——两行两列的单位阵。

经过卡尔曼滤波器预处理后的心电信号如图1所示。

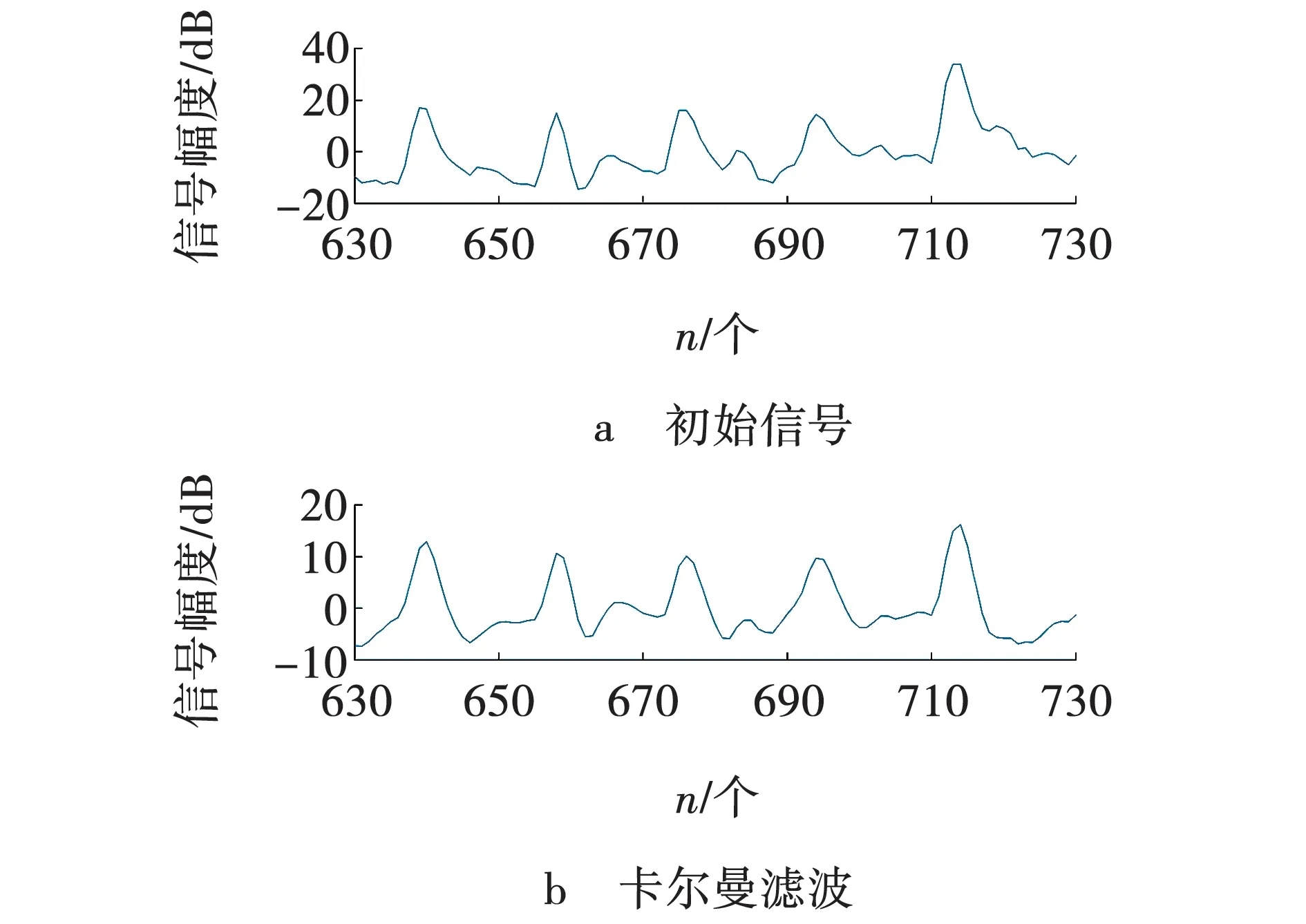
图1 初始信号与滤波信号

2 心电图T波段选取

T波位于 S-T 段之后，正常T波方向与R波的方向一致，呈现钝圆型，如图2所示。

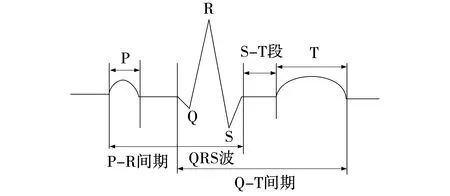
图2 正常心电图示意

心电图中的R波由于波峰明显，识别方便，设定好时间窗口的长度和取样时间，搜寻出极大值点，该点极为QRS波群波峰的位置。图3为一段经过卡尔曼滤波预处理之后的R波峰值心电图，峰值用星型符号标出。

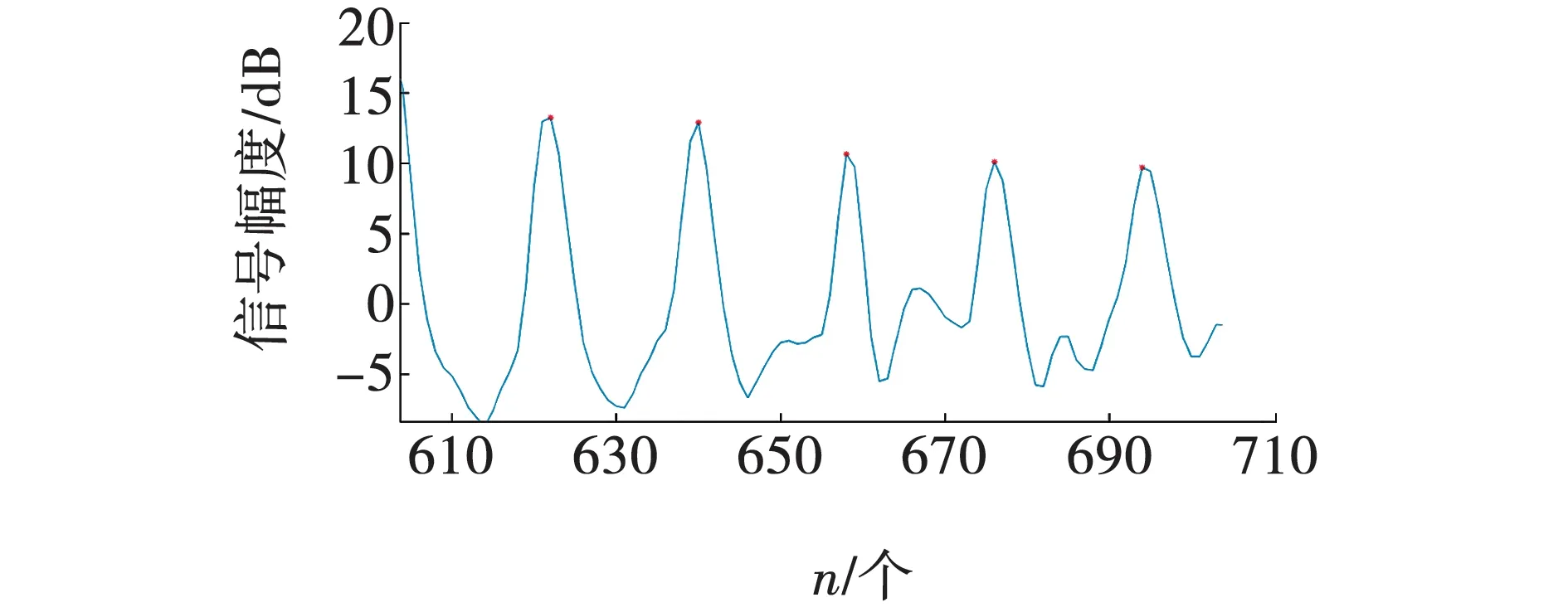
图3 R波波峰检测

以测到的R波为基准点，在R波之后定义一个包含有T波的长度和位置的滑动窗口，将得到的候选段截取出来，其中，每个T波候选段截取分两步。

步骤1根据 RR 间期估算出T波起点[6]

式中：T——T波起点；

tRR——心电图上两个R波之间的间隔时间。

步骤2根据 RR 间期估计T波的长度TL，已知T波通常滞后R波50 ms左右，估算T波的长度为

3 算法设计

3.1 LSTM-CNN组合的神经网络模型

CNN是一种前馈神经网络，由卷积层、池化层和全连接层组成，可以提取局部特征，保持权值共享，降低过拟合，但卷积核的大小尺寸决定了难以学习到序列数据的前后时间逻辑，而LSTM通过引入记忆单元和门机制能够弥补这一缺陷。因此，文中提出LSTM和CNN组合的深度学习模型来完成心电图的自动分类[7]。LSTM-CNN模型如图4所示。

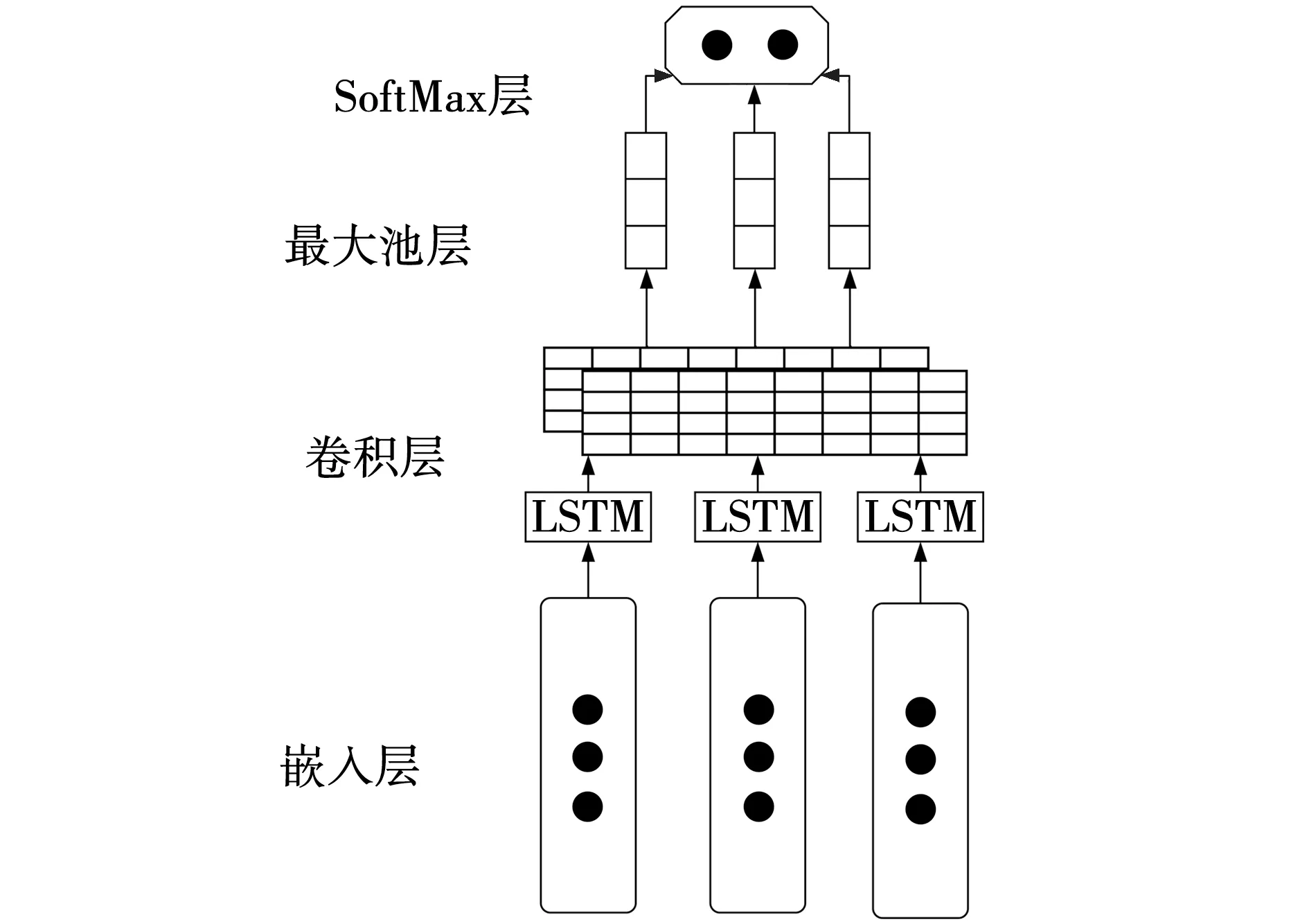
图4 LSTM-CNN网络模型

3.2 鲸鱼优化算法

鲸鱼优化算法是[8]一种新型的智能优化算法。该算法是一种模拟座头鲸捕食行为的仿生智能优化算法,算法流程如图5所示。

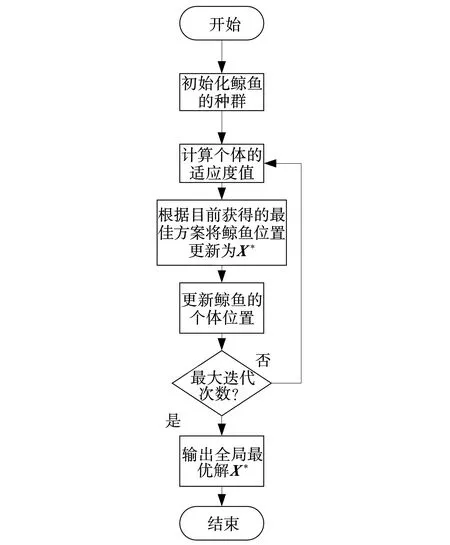
图5 鲸鱼优化算法流程

(1)WOA算法首先随机初始化一组解，在每次迭代中，搜索代理根据随机选择的搜索代理或到目前为止获得的最优解更新它们的位置，则

(4)

X(t+1)=X*(t)-A·D,

(5)

式中：D——搜索代理到目标食物的距离向量；

t——当前迭代次数；

C、A——系数向量；

X*——局部最优解；

X——位置向量。

(2)将参数a由2随迭代次数降为0，则有

C=2·r,

A=2a·r-a,

式中,r——0至1之间的随机数。

(3)当|A|≥1时，根据式(6)、(7)选择随机搜索代理；当|A|<1时，根据式(6)选择最优解更新搜索代理位置。

D=|C·Xr-X(t)|,

(6)

X(t+1)=Xr-A·D,

(7)

式中,Xr——随机获得的位置向量。

(4)螺旋更新位置。鲸鱼首先计算出自身位置到猎物位置之间的距离，接着在鲸鱼与猎物之间创建一个螺旋等式，来模拟鲸鱼螺旋状移动的行为。

D′=|X*(t)-X(t)|,

(8)

X(t+1)=D′·ebl·cos 2πl+X*(t)，

(9)

式中:D′——最佳距离向量；

b——常量；

l——-1到1之间的随机数。

鲸鱼在捕食的过程中有收缩包围和螺旋更新两种机制，因此，用这两种方法进行数学建模。假定鲸鱼用式(5)或式(9)更新自身位置的概率各为50%，更新位置为

式中,p——[0，1]之间的随机数。

3.3 WOA优化LSTM-CNN神经网络模型

WOA算法优化的过程，是优化网络中的各个参数，使得网络的训练误差最小的过程[9-11]。适应度可以评价个体的性能，建立个体适应度与网络验证误差的关系，选择网络参数保证网络参数全局最优。适应度公式的评价能力直接决定整个优化的效果。算法训练流程分为三步。

步骤1在优化过程中，计算适应度值。适应度函数的设计，通过鲸鱼优化算法优化LSTM-CNN神经网络的参数，优化函数为

f(·)=fCNN(α,β1,β2,β3,β4,N,K1,K2,K3)。

(10)

这九个参数分别表示LSTM-CNN的学习率，LSTM-CNN的4个偏移变量，特征金字塔网络(FPN)的分层数量，多个层次的加权系数K1～K3。

步骤2优化算法的优化变量。假设优化算法的个数是n，则遗传优化变量是n×9的一个二维矩阵，则每个优化变量，均有n个遗传优化变量来进行迭代优化。

假设遗传优化变量为Xn×9，即：

α=Xn×1[1],β1=Xn×1[2],β2=Xn×1[3],

β3=Xn×1[4],β4=Xn×1[5],

N=Xn×1[6],K1=Xn×1[7],

K2=Xn×1[8],K3=Xn×1[9]。

步骤3通过上述的过程之后，可以根据式(10)计算出每个变量对应的适应度值fitness。对于LSTM-CNN的最优参数，假设为：αo、βo1、βo2、βo3、βo4、No、Ko1、Ko2、Ko3。此时这组参数下对应的LSTM-CNN，其训练误差将达到最优。此时通过优化后，得到一个由N层构成的LSTM-CNN神经网络，假设为：LSTM-CNN1,LSTM-CNN2,…,LSTM-CNNN。

通过这N个LSTM-CNN，对信号进行多尺度的训练。

假设训练后得到的神经网络权值分别为{wij}1,{wij}2,…,{wij}N。

设置N最大值为4，得到的最终的LSTM-CNN神经网络的权值w，可以表示为

wij=K1×{wij}1+K2×{wij}2+...+

(1-K1-K2-...)×{wij}N。

图6是T波识别构建的神经网络模型。将心电信号进行特征提取出T波候选段，输入到LSTM，由LSTM层提取时序特征，将输入生成一个新的序列数据，LSTM层的输出紧接着输入到可以提取局部特征卷积层中。在卷积层中加入了特征金字塔网络(FPN)。FPN算法可以将具有不同尺寸，不同特征的目标区分开来。实验分3层，输出目标的复杂度随着层数的增加而增加。在卷积层1-1与卷积层1-2中都分布着一个3×3的卷积核和3×3的空洞卷积核。下采样层对卷积层输出的特征向量进行池化，将原输入的特征压缩为原来的一半，最后由输出层计算结果。整个LSTM-CNN网络搭建完成后，置入WOA中进行优化，获得最优网络层参数。

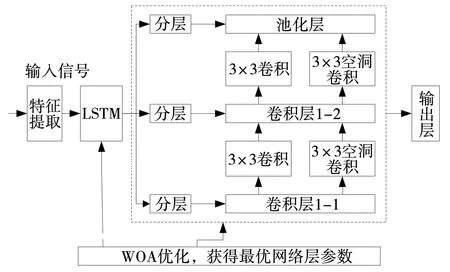
图6 T波识别神经网络结构

4 实验与结果分析

实验采用464名某煤矿公司井下一线作业工人采集的心电数据作为样本集，平均年龄23～55岁，均为井下一线煤矿工人，工作时间为1～15 a，均为成年男性，所有信号都以125 Hz的频率采样，通过矿用智能手表发送到调度室监测平台上，最终数据集中划分为训练集样本18 000个，测试集样本7 700个。

实验运行环境 Win10 64 位操作系统，CPU 为英特尔i7-8750H，主频率2.20 GHz，采用 MatlabR2019a进行实验，内存大小为16 GB，显卡为GTX 1060，程序所使用算法软件包为 DeepLearnToolbox-master。

在心电图分类的问题中，通常以准确率(PA)、特异性(Sp)和敏感性(Se)为指标来评价模型的性能。文中运用了混淆矩阵的四个评价指标，即算真阳性(nTP)、假阳性(nFP)、假阴性(nFN)、真阴性(nTN)这四个参数来表示准确率、特异性和敏感性。

准确率为预测正确的样本占整个样本的比例为

特异性是指预测为阴性的样本数占实际阴性样本数的比例为

灵敏度指预测为阳性的样本数占实际阳性样本数的比例为

实验中的WOA优化算法的最大迭代次数为50，初始化种群规模为100，搜索空间维数为9，学习率优化范围是[0.001,0.2]，图7为损失函数变化曲线。

图7 WOA优化过程

由图7可知，训练情况收敛，得出的适应度值组成的向量。根据实验结果后发现，当迭代次数过小则会导致整个模型无法充分学习心电信号特征，使模型总体识别效率降低。若将迭代次数设定的太小则会过拟合，同时也会使得仿真时间延长。经过反复验证，当将最大迭代次数设置为200时，能够很好地对信号特征进行学习，使目标函数收敛。在仅CPU的训练条件下，训练过程所需时间为40.8 h。

为了验证LSTM-CNN网络模型的训练效果，文中将7 700个测试集划分为正常T波、T高尖和T波倒置三部分，分别进行分类。分类结果如表1所示。

表1 分类结果

识别算法识别出的T波高尖和T波倒置如图8和9所示。

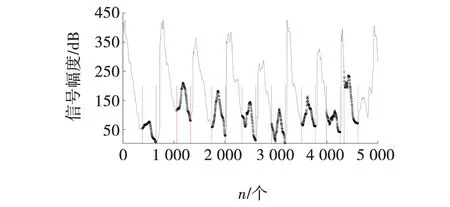
图8 T 波高尖

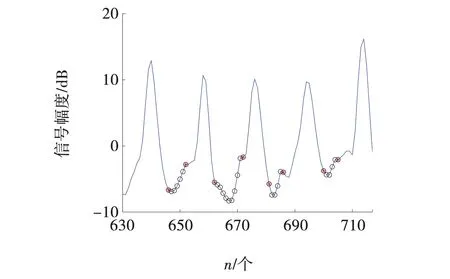
图9 T 波倒置

图10的ROC曲线展示了文中的算法与传统机器学习算法SVM性能比较，从图10中可以看出,经过WOA优化的LSTM-CNN算法准确率显著高于SVN。AUC值高达0.993，证明方法的识别能力强，用于有效检测心律失常的价值最佳。

表2为已有算法得到的结果。从表2可知，基于传统机器学习方法识别心电信号的准确率较低，而且对T波异常的识别能力比较差，容易发生误诊、漏诊。

图10 ROC曲线比较

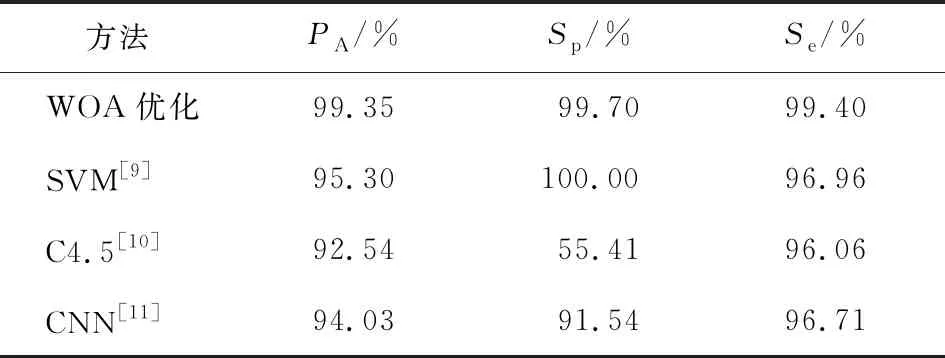
表2 所提方法性能指标与其他方法对比

研究表明，常用的特征提取函数的拟合能力有限，未能完全捕捉到心电图中的隐藏特征。通过对比可以得出，通过WOA优化LSTM-CNN神经网络的参数，将误差最小化，利用 LSTM 提取心电图的时序特性，FPN改进CNN网络的特征提取方式，可以使最终输出的特征更好地表示出输入信号的信息，模型输出结果可以达到较高的准确率。

5 结 论

(1)分析了心电图中T波的特点，运用时间搜索窗口提取了T波段位置，提出了基于LSTM-CNN的神经网络模型识别T波，通过WOA优化算法优化神经网络参数，训练并计算获得每个个体对应的适应度值作为神经网络的参数，此方法可以有效改进陷入局部最优。

(2)在训练与测试阶段选取了2万多个样本，测试的结果准确率为99.35%，特异性为99.70%，灵敏度为99.40%，对于准确有效的检测出煤矿工人的心律失常具有较好的作用。因此，对煤矿工人进行心电图检查，减少职业病的发生具有十分重要的指导意义。