基于双闭环P+前馈的移动机器人路径跟随控制
沈显庆, 孙启智, 马志鹏
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
移动机器人比一般的机器人有更大的灵活性,目前广泛应用于救灾排险[1]、资源勘探[2]和物流运输[3]等领域。移动机器人路径跟随控制[4]是移动机器人研究中的重要问题之一。路径跟随是在机器人进行路径规划[5]后对其进行运动控制,使其沿着目标路径运动的过程。
当前,移动机器人路径跟随控制受到诸多研究者的关注。其中,PID控制具有控制原理简单、易于实现等优点,常用在移动机器人的路径跟随控制中[6]。许洋洋等[7]采用PID控制与神经网络相结合的方法,动态调整控制参数,提高了控制系统运动的稳定性。孟祥萍等[8]提出了在比例项和积分项前乘以α、β的积分分离式PID控制算法,提高了系统的响应速度,增强了系统的鲁棒性。冯剑等[9]分析了移动机器人的动态特性,设计了直接反馈线性化的 PID 控制器方法,该方法简单易行,具有较高的跟踪精度和较好的抗干扰能力。李林琛等[10]通过遗传算法对个体进行编码,采用将遗传算法中个体的适应度函数改为移动机器人的PID 控制精度的方法调整PID参数,提高了机器人的自调节能力,降低了路径跟随过程中的跟踪误差。在高精度的伺服控制中,可以通过前馈控制的方法提高系统的跟踪性能。笔者利用P+前馈控制原理,建立了的机器人运动学模型,设计双闭环P+前馈的控制器,通过仿真验证该方法与经典PID控制的路径跟随能力。
1 机器人运动学模型的建立
以Hawkbot差动机器人为例,该机器人由左电机驱动的驱动轮L、右电机驱动的驱动轮R和万向轮组成,通过控制两个电机的转速和转动方向,使左右两个驱动轮产生“差速”,从而控制机器人的运动。机器人运动模型如图1所示。
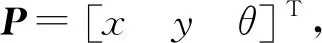

式中:v——机器人的线速度;
w——机器人的角速度。
移动机器人的运动学模型可表示为:

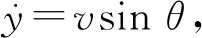


图1 机器人的运动学模型
2 P+前馈补偿控制
2.1 经典PID控制
PID 控制作为最成熟的控制算法具有鲁棒性好、可靠性高等优点,目前被广泛应用于运动控制当中[11]。经典PID控制系统由PID控制器和被控对象构成,如图2所示。

图2 经典PID控制系统原理
经典PID控制器的输入输出偏差:
e(t)=yd(t)-y(t),
式中:yd(t)—— 输入给定值;
y(t)—— 输出值。
PID的控制规律:

式中:kp—— 比例系数;
ki—— 积分时间常数;
kd—— 微分时间常数。
传递函数G(s)为
2.2 P+前馈控制原理
PID参数难以整定,对于允许有静差的系统,可以适用简单的比例控制,使稳态误差在允许的范围内。在闭环系统连续时,利用前馈的思想对比例控制器进行前馈补偿,从而提升系统的跟踪性能,其结构如图3所示。
总控制输出为
u(t)=up(t)+uf(t),
式中:up(t)—— 比例控制输出;
uf(t)—— 前馈控制输出。
离散化后
u(k)=up(k)+uf(k)。
3 双闭环P+前馈控制器设计
基于P+前馈的控制算法跟踪性能较高,故采用前馈补偿的比例控制作为运动控制算法。根据机器人运动学方程可知,系统有2个自由度,3个输出变量,故该系统为欠驱动系统。通过设计位置控制律v可实现[xy]两个位置变量的主动跟踪,同时设计姿态控制律w实现机器人前进方向与x轴方向夹角的随动跟踪。
3.1 位置控制律
取[xdyd]为目标路径,则位置跟踪误差:
xe=x-xd,
ye=y-yd,
式中:xe——x方向跟踪误差;
ye——y方向跟踪误差。
可推出位置误差的跟踪方程:
令
vcosθ=u1,
vsinθ=u2。
则
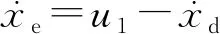
则
取kp1>0,则当t→∞时,xe→0。

则
取kp2>0,则当t→∞时,ye→0。
令
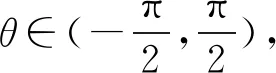
(1)
式(1)中的θ为满足位置控制律的角度,实际情况中θ≠θd,位置控制律无法准确地实现,造成闭环跟踪系统的不稳定。针对这个问题,可将θ视作理想角度θd,即
实际的位置控制律为
3.2 姿态控制律
取θd为目标路径跟踪角度,则跟踪的角度误差:
θe=θ-θd,
可推出跟踪的角度误差的跟踪方程:
对其取P+前馈控制设计控制器,即
则
取kp3>0,则当t→∞时,θe→0。
3.3 闭环系统的设计
采用双闭环控制的方法,设计位置[xy]的跟踪为系统外环,夹角θ的跟踪为系统内环。外环中的位置子系统产生姿态指令信号θd传递给内环系统,内环通过滑膜控制律实现夹角θ的快速跟踪。双闭环控制系统结构如图4所示。

图4 具有双闭环的移动机器人系统结构
针对角度θ与目标跟踪角度θd不完全相等导致的闭环系统不稳定问题,可设计较大的姿态控制器增益kp3,让内环收敛速度比外环收敛速度更快,使得θ快速跟踪θd,避免系统不稳定的问题。
4 仿真结果与分析
为验证基于P+前馈控制算法的跟踪性能,设被控对象为
取输入信号为:yd(k)=0.5sin(6πt),采样时间为1 ms。在Matlab软件中分别对经典PID算法和基于P+前馈的控制算法进行仿真对比,仿真结果如图5~8所示。
由图5仿真结果可以看出,在正弦响应跟踪时,经典PID控制和基于P+前馈控制均能够快速对正弦曲线进行跟踪。但从跟踪结果可以看出,经典PID控制跟踪时与正弦曲线始终无法完全重合,跟踪效果欠佳,而基于P+前馈控制跟踪时能够基本与正弦曲线重合,跟踪效果较好。

图5 正弦响应跟踪效果

图6 正弦响应跟踪误差

图7 阶跃响应跟踪效果
从图6的误差曲线可以看出,经典PID控制在正弦响应跟踪时跟踪误差来回波动无法收敛,基于P+前馈控制能够快速跟踪并基本消除跟踪误差。
由图7中阶跃响应输入时的仿真结果可以看出,经典PID控制跟踪时有一定的超调量,跟踪效果不理想,而基于P+前馈控制的跟踪无较大波动,跟踪较经典PID控制更加稳定平稳,能够提高系统的跟踪性能。
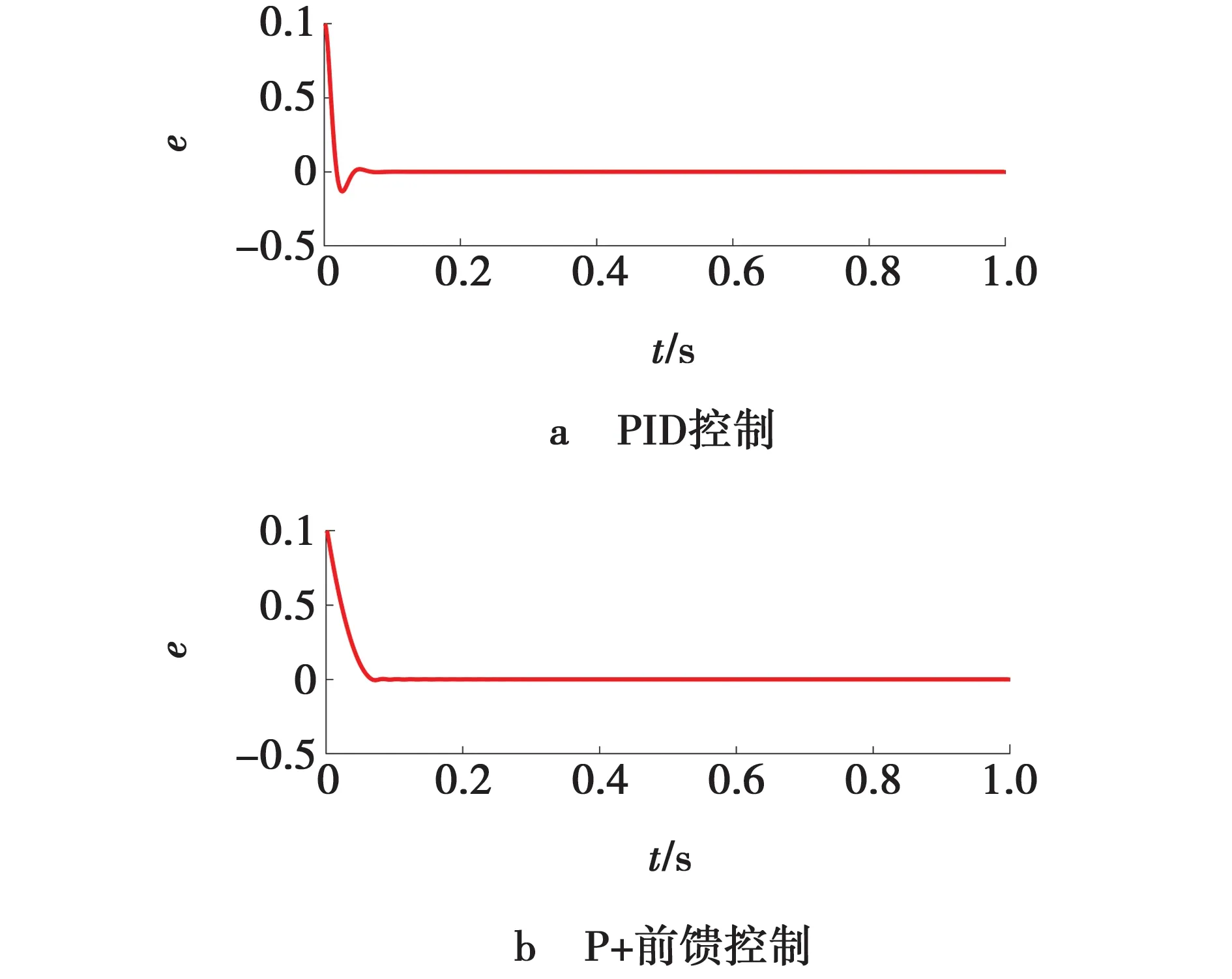
图8 阶跃响应跟踪误差
从图8的阶跃响应跟踪误差仿真结果可知,经典PID控制跟踪误差曲线的平滑性较差,而基于P+前馈控制跟踪误差曲线能够快速收敛,效果较为理想。为验证双闭环P+前馈控制器的设计,通过Matlab进行仿真实验,搭建的Simulink仿真模型如图9所示。
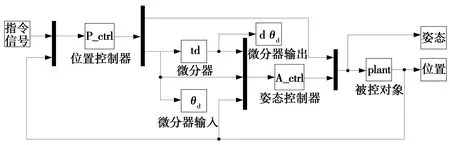
图9 Simulink仿真模型

从图10和图11可以看出,基于双闭环的P+前馈控制能够快速对目标路径进行跟随,从图12可以看出,θd最大值为0.961 3,θd∈(-π/2,π/2),能够满足双闭环P+前馈控制器的设计要求。

图10 机器人的运动轨迹

图11 位置和角度的跟随效果

图12 微分器的输入与输出
5 结 论
(1)在正弦响应输入下,经典PID控制的跟踪误差存在较大的波动,其标准差约0.020 84,平均误差约为0.006 254,P+前馈控制的跟踪误差能够迅速收敛,其标准差约为0.006 71,平均误差约为0.001 293。
(2)在阶跃响应输入下,经典PID控制存在较大超调,约为14.1%,P+前馈控制有效减小了超调,约为0.6%。
(3)双闭环的P+前馈控制能够快速跟随目标路径,目标路径理想跟随角度最大值为0.961 3 rad,满足双闭环P+前馈控制器的设计要求。

