基于建模思想的高职数学混合式教学设计

杨树清 黄慎 詹鸿

【摘要】本文基于数学建模思想及布鲁纳学习理论，以高阶导数为例，通过实际案例的引入分析与求解、课程信息化平台及资源的利用进行混合式教学设计与实施，目的在于促进三维目标的实现.

【关键词】布鲁纳学习理论;高阶导数;混合式教学

著名科学家钱学森说过：“信息时代高技术的竞争本质上是数学技术的竞争.”很多技术的发展都离不开数学模型，数学的应用已渗透到了各个领域.高等数学是高职生的一门必修基础课，学好高等数学是学好专业课程的前提.我们基于数学建模思想及布鲁纳学习理论，利用信息化平台及课程资源进行混合式教学设计，将数学知识与建模思想相结合，让学生切身感受数学是应用于实际，服务于实际的，真正做到学以致用.接下来以高阶导数为例进行教学设计并分析实施效果.

一、教学分析

1.教学内容及授课对象

本节课以汽车的刹车性能为切入点，讲解高阶导数的概念及计算.授课时长1学时.授课对象为2019级汽车学院一年级学生.

2.学情分析

高职生作为一类学生群体，来源和成分具有多样性，学习目标不明确，学习积极性不足.知识基础：通过前导知识的学习，学生已经掌握导数的定义、基本公式和求导法则;能力基础：学生动手能力强，推理能力不足，时常找不准问题切入点，对概念、公式的记忆能力较弱且容易遗忘，对知识点的应用能力不足;素质基础：学生具有探究精神但思维缺乏严谨性，主动学习的意识较弱.

3.教学目标

第一，知识目标.让学生掌握高阶导数的定义、表示方法及其计算.第二，能力目标.培养学生从数学的角度刻画问题，建立模型，解决实际案例的能力.第三，素质目标.增强团队合作意识，发扬刻苦钻研精神，树立严谨治学态度，提升学生数学文化素养.

4.教学重难点及解决措施

根据专业人才培养方案以及后续课程的需要，本次课重点介绍高阶导数的定义及计算，其中难点为n阶导数的计算.学生通过自己设计导数的符号，体会符号背后的意义和设计符号的原则.

二、教学策略

根据教学内容以及学生的学习特点，本课程遵循淡化数学理论证明、增强学生建模意识的原则进行教学设计.充分利用课程信息化平台和资源，由实际案例进行引入，激发学生自主学习、相互学习的能力.

三、教学过程

1.教学过程

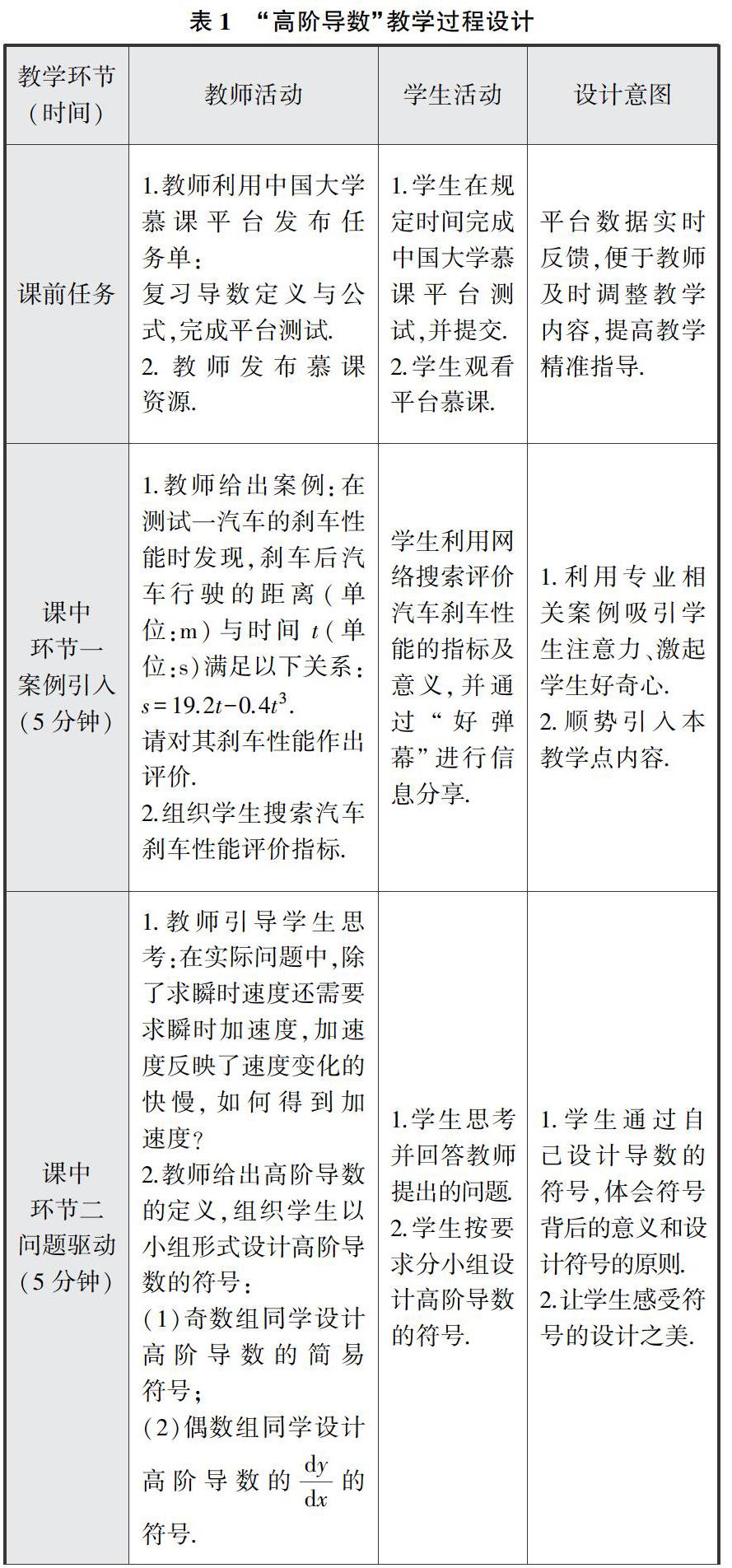
复习导数定义与公式，完成平台测试.

2.教师发布慕课资源.

1.学生在规定时间完成中国大学慕课平台测试，并提交.

2.学生观看平台慕课.

平台数据实时反馈，便于教师及时调整教学内容，提高教学精准指导.

（5分钟）

1.教师给出案例：在测试一汽车的刹车性能时发现，刹车后汽车行驶的距离（单位：m）与时间t（单位：s）满足以下关系：s=19.2t-0.4t3.

请对其刹车性能作出评价.

2.组织学生搜索汽车刹车性能评价指标.

学生利用网络搜索评价汽车刹车性能的指标及意义，并通过“好弹幕”进行信息分享.

1.利用专业相关案例吸引学生注意力、激起学生好奇心.

2.顺势引入本教学点内容.

（5分钟）

1.教师引导学生思考：在实际问题中，除了求瞬时速度还需要求瞬时加速度，加速度反映了速度变化的快慢，如何得到加速度？

2.教师给出高阶导数的定义，组织学生以小组形式设计高阶导数的符号：

（1）奇数组同学设计高阶导数的简易符号;

（2）偶数组同学设计高阶导数的dydx的符号.

1.学生思考并回答教师提出的问题.

2.学生按要求分小组设计高阶导数的符号.

1.学生通过自己设计导数的符号，体会符号背后的意义和设计符号的原则.

2.让学生感受符号的设计之美.

（15分钟）

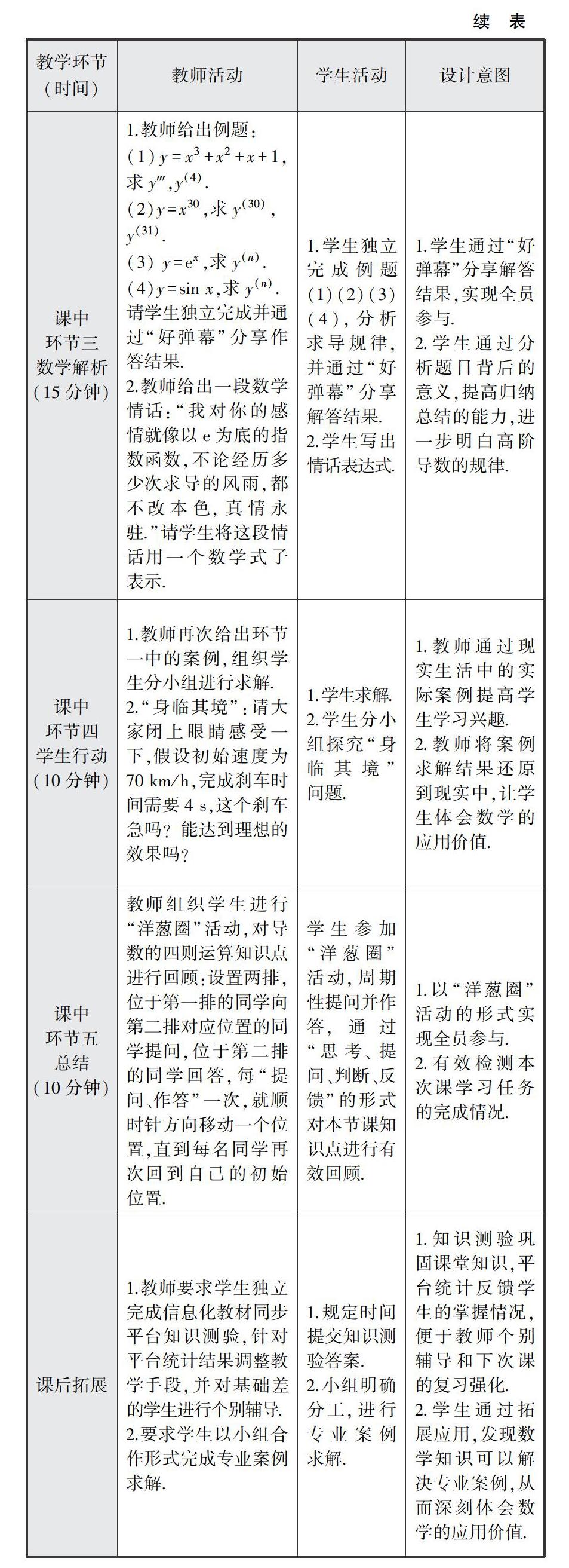
1.教师给出例题：

2.教师给出一段数学情话：“我对你的感情就像以e为底的指数函数，不论经历多少次求导的风雨，都不改本色，真情永驻.”请学生将这段情话用一个数学式子表示.

1.学生独立完成例题（1）（2）（3）（4），分析求导规律，并通过“好弹幕”分享解答结果.

2.學生写出情话表达式.

1.学生通过“好弹幕”分享解答结果，实现全员参与.

2.学生通过分析题目背后的意义，提高归纳总结的能力，进一步明白高阶导数的规律.

课中环节四

学生行动

（10分钟）

1.教师再次给出环节一中的案例，组织学生分小组进行求解.

2.“身临其境”：请大家闭上眼睛感受一下，假设初始速度为70 km/h，完成刹车时间需要4 s，这个刹车急吗？能达到理想的效果吗？

1.学生求解.

2.学生分小组探究“身临其境”问题.

1.教师通过现实生活中的实际案例提高学生学习兴趣.

2.教师将案例求解结果还原到现实中，让学生体会数学的应用价值.

课中环节五

总结

（10分钟）

教师组织学生进行“洋葱圈”活动，对导数的四则运算知识点进行回顾：设置两排，位于第一排的同学向第二排对应位置的同学提问，位于第二排的同学回答，每“提问、作答”一次，就顺时针方向移动一个位置，直到每名同学再次回到自己的初始位置.

学生参加“洋葱圈”活动，周期性提问并作答，通过“思考、提问、判断、反馈”的形式对本节课知识点进行有效回顾.

1.以“洋葱圈”活动的形式实现全员参与.

2.有效检测本次课学习任务的完成情况.

课后拓展

1.教师要求学生独立完成信息化教材同步平台知识测验，针对平台统计结果调整教学手段，并对基础差的学生进行个别辅导.

2.要求学生以小组合作形式完成专业案例求解.

1.规定时间提交知识测验答案.

2.小组明确分工，进行专业案例求解.

1.知识测验巩固课堂知识，平台统计反馈学生的掌握情况，便于教师个别辅导和下次课的复习强化.

2.学生通过拓展应用，发现数学知识可以解决专业案例，从而深刻体会数学的应用价值.

2.考核评价

我们综合考查学生课前、课中、课后的个人完成情况和小组活动参与度，实现了过程评价和多元评价，具体评分占比见表2.

四、教学反思

1.特色与创新

环节二中的符号设计，学生通过自己设计导数的符号，体会符号背后的意义和设计符号的原则，感受数学的符号美;环节四中“身临其境”的设计，将案例求解结果还原到现实中，让学生切身感受到数学的应用价值;环节五中的“洋葱圈”活动在富有趣味性的基础上，能有效检测学生本次课学习任务的完成情况，并实现全员参与.

2.不足与改进

小组活动中存在个别学生对小组其他成员过于依赖的现象，在后续教学中可适当增加个人加分环节;监控和激励措施也应加强，从而提高课堂上全体学生的参与度;教师需不断与时俱进，持续更新课程资源.

五、结 语

实践证明，掌握一定的数学建模思想和方法是坚实数学基础的重要组成部分，怎样有机地把数学建模的思想和方法融入大学数学课程是当前大学数学教学改革的一个重要切入点.我们的教学设计思路是希望通过引入案例求解，在完成知识点教学的同时，逐步培养学生的数学建模思想，从而更好地引导学生将数学知识的学习与應用相结合，消除“数学无用”的偏见，而这项艰巨的改革工作也推动着教师不断更新自身知识体系，从而培养出更多的优秀人才.

【参考文献】

[1]韩中庚.数学建模实用教程[M].北京：高等教育出版社，2012.

[2]黄慎，李海霞.高职生高等数学学习现状分析及提高对策[ J].黑龙江科学，2020（11）：152-153.

[3]谢歆鑫，等.基于专业应用的高职数学混合式教学设计与实施：以曲线凹凸性及拐点为例[J].黑龙江科学，2020（1）：22-25.