扭转陀螺章动与进动现象的实验规律研究
李定波,吴秀文,董爱国
(中国地质大学(北京) 数理学院,北京 100083)
章动是陀螺的对称轴在铅垂面内上下摆动的运动,图1 是扭转陀螺装置实物图。组装、调整装置,然后释放该陀螺系统,会发现陀螺产生章动[1-3]和进动[4-5]现象,常见的进动仪就是基于该现象设计的[6]。但是,扭转陀螺在模拟进动和章动时仍存在无法生动地模拟章动扬角的过程[7]、仪器不便携带、润滑不方便等问题。旋转刚体(如陀螺转子、自旋卫星等)受到力矩的干扰或由于角动量矢量在惯性空间中方向的改变就会产生章动运动。在无法直接观测到外界情况时,通过陀螺章动的特性能够完成对物体姿态的控制,因此陀螺的章动研究对于航空航天领域中卫星的姿态调整、瞄准精度的设置以及惯性制导[8]有着重要的意义。目前,国内外关于陀螺章动的研究主要局限在其无外力作用,或受脉冲力矩作用、恒定力矩作用下的运动规律研究[9-11],而在变化力矩作用下的运动研究较少,有学者利用动静法建立陀螺仪运动方程,分别推导出了无阻尼和有阻尼条件下的进动与章动模型[12],并指出在章动方向上角度变化受到重力矩引起的章动和铅垂轴方向阻尼力矩引起的转子轴进动两个方面的影响[13-15],但建立的陀螺仪模型中并没有陀螺自旋产生的自旋角动量对章动的影响,研究较为局限。
本文对自由陀螺系统在变力矩下陀螺的章动和进动情况进行深入的研究,同时建立一个研究复杂力学问题的进动与章动模型,对这一款扭转陀螺装置的章动和进动的机理进行了详细的分析,给出了相应的数学表达式,并通过实验加以验证。

图1 扭转陀螺装置实物图
1 实验器材和方法
实验所用器材包括具有一定扭转阻力的尼龙绳和陀螺(图2)。实验中绳子有效长度为20 cm,陀螺总质量为150 g,轮子质量为100 g,轮子半径为30 mm。实验时需将其外轮系紧在有一定扭转阻力的尼龙线上(陀螺通过该线竖直悬放),给尼龙线一定初始扭转力矩,且使内轮以一定角速度自旋,而后释放该陀螺系统。

图2 陀螺与尼龙线实物图
测试分析方法:实验前,用红色记号笔标记陀螺质心位置,用蓝色记号笔标记陀螺自旋周期的采集位置。采用PIC-AL00 录像机拍摄镍盘的转动过程。对录像资料采用Tracker 软件追踪分析陀螺运动,并在软件中读取陀螺质心的位移、陀螺进动周期、绳子与竖直方向的夹角和陀螺自转周期。由于陀螺自旋时轮子上各点均做角量规律相同的自旋运动,在研究陀螺自旋周期变化规律时,以轮子上某任意点为研究的代表点(本实验以蓝色记号笔标记点为研究代表点)。实验数据测量均为6 次,取其平均值。为了排除实验装置、操作等造成的误差的影响,先用A 类标准不确定度的计算方法对数据进行处理,但由于测得值的不确定度来源不止一个,所以要合成标准的不确定度。标准偏差的计算公式为
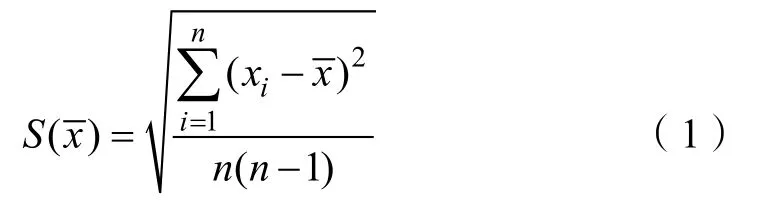
其中,是测量值xi的算术平均值,n是测量次数。标准不确定度的计算公式为

其中,f是估计值y与测量值ix的函数关系式。
2 陀螺运动分析
2.1 陀螺章动分析
陀螺的运动由章动、进动和自旋运动构成,章动运动受到绳子扭转力矩的作用,进动运动受到重力矩的作用,而自旋运动受到摩擦等阻力的作用,根据以上3 种运动的不同组合形式可将陀螺系统的运动分为3 个阶段:触发阶段、衰减阶段和反向阶段。其受力分析如图3 所示。根据角动量定理,得到:

其中,M绳是绳子对陀螺的扭矩,ΔL是陀螺章动过程中的角动量变化,Δt是陀螺章动过程的时间变化。根据图3 中的几何关系,得到:

其中,L是陀螺自旋产生的角动量,Δθ是陀螺章动的微小角位移。联立公式(3)和(4)可得章动角速度为


图3 陀螺章动受力矩示意图
由于在实际实验中,绳子对陀螺的扭矩会随着绳子的偏移而产生偏移,因此将扭矩分解,如图3 所示,仅扭矩的竖直分量M绳⊥对陀螺的章动有贡献,因此可得章动角速度为

由式(6)可见,章动角速度与绳子对陀螺的扭矩成正比,与陀螺自旋角动量成反比。
2.2 陀螺进动分析
由于陀螺的章动使其质心偏离初始的竖直轴一定距离,产生重力臂r,因此在重力矩M重=r·G(G是陀螺的重力)的作用下陀螺产生绕其初始竖直轴的进动,陀螺受力如图4 所示,根据角动量定理,得到

其中,ΔL进是陀螺进动过程中的角动量变化(方向垂直纸面向里)。陀螺在进动时转过微小角位移时产生的与自旋角动量的几何关系类似于章动,得到:

其中,Lx是陀螺自旋角动量,Δφ是陀螺进动的微小角位移。联立公式(7)和(8)可得进动角速度:

其中,陀螺章动的角位移θ=α+β(0°<θ<90°),α是绳子与竖直方向的夹角,β是绳子连接点与陀螺质心连线所在的直线与绳子延长线的夹角,L是陀螺自旋角动量。
综合以上分析,根据图4 的几何关系,得到:


图4 陀螺系统进动示意图
由于A与式(12)中其他项相差较多的数量级,所以A对合磁力矩的影响较小。由式(12)及其相应的分布曲线可知(见图5),当0°<θ<45°时,进动角速度与章动角成正比,当45°≤θ<90°时,进动角速度与章动角成反比;进动角速度与绳子的有效绳长和陀螺的进动半径r成正比,与陀螺自旋产生的角动量成反比。

图5 式(12)的分布曲线图
3 结果与讨论
图6 是陀螺的章动角度随时间变化的关系曲线。由图6 可见,陀螺章动过程中在20~35 s 之间存在比较稳定的章动角,陀螺的稳态章动角约为30°。图7是陀螺的进动周期随时间变化的关系曲线。由图7 可见,陀螺进动过程中在20~38 s 之间存在比较稳定的进动周期T,约为0.58 s,根据角速度与周期的关系式可得,陀螺的稳态进动角速度约为10.83 rad/s。38 s 后陀螺系统能量衰减较为明显,陀螺系统运动趋于静止。此结论与洪子昕[1]的研究不一致,由于洪子昕等人在实验时绳子的扭转圈数较少,因此只发现陀螺的章动角到达最大值后一直衰减到零,未发现陀螺存在稳定进动角速度的现象。
本实验中l=20 cm,G=1.5 N,L=0.028 kg·m2/s。由式(12)计算得出理论的进动角速度为10.50 rad/s,实验所得进动角速度与理论值大致相近,偏差≤3.14%。
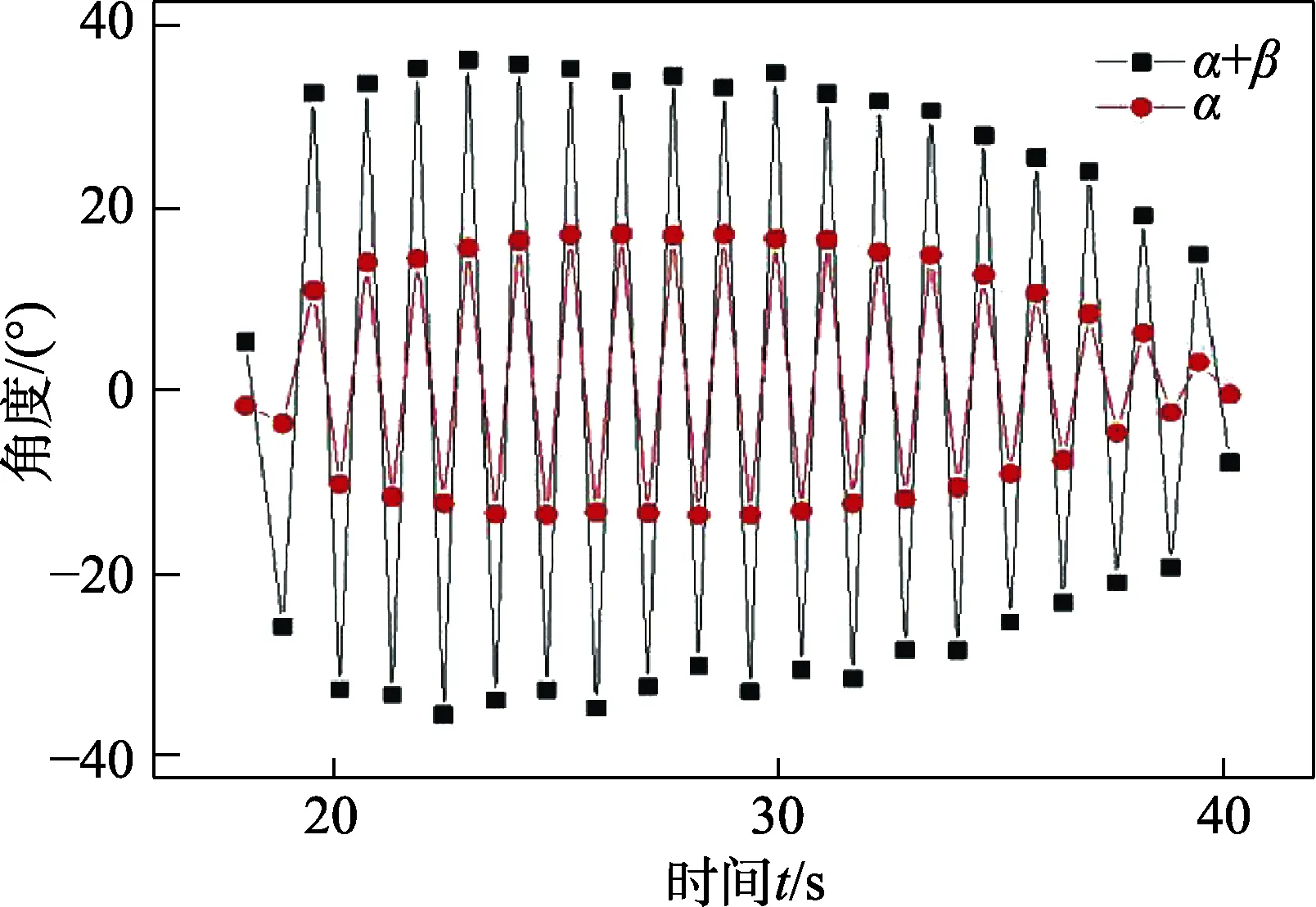
图6 陀螺章动角度随时间的变化
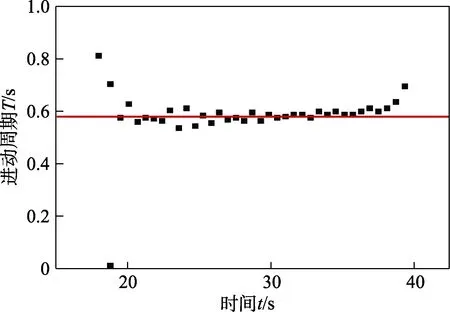
图7 陀螺进动周期随时间的变化
图8 是陀螺的进动角速度随进动半径变化的关系曲线,图中理论值是根据式(9)计算所得。由图8可见,当陀螺的进动半径由2 cm 增至5.2 cm 时,陀螺的理论进动角速度由4.2 rad/s 增至13.1 rad/s,实际进动角速度由4.2 rad/s 增至8.2 rad/s。陀螺的进动半径越大,进动角速度的实验值与理论值的偏差越大。因为随着陀螺进动半径的增大,受绳子的颤动和疲劳的影响,损耗在绳子上的能量增大,从而导致进动角速度的实验值与理论值的偏差增大。

图8 陀螺进动角速度随进动半径的变化
图9 是陀螺的自转周期随时间变化的关系曲线。由图9 可见,当时间由16.000 s 增至27.992 s 时,陀螺的自转周期由0.068 s 增至0.116 s;当时间由31.992 s增至39.980 s时,陀螺的自转周期由0.136 s 增至0.184 s。对于时间在16.000~27.992 s 范围内的数据进行线性拟合得到的关系式为
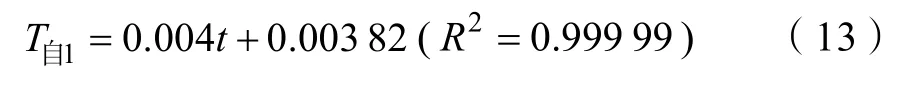
对于时间在31.992~39.980 s 范围内的数据进行线性拟合得到的关系式为
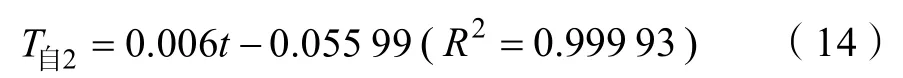
其中,R2表示拟合优度,R2的值越接近1,说明回归直线对实验值的拟合程度越好。该结果说明,陀螺的自转周期随时间分段线性变化,此结论与陈宗强等[4]的研究结果一致。

图9 陀螺自转周期随时间的变化
图10 是陀螺质心在水平方向上的位移随时间变化的关系曲线。由图10 可见,在水平方向上,陀螺质心在21~35 s 存在比较稳定的运动轨迹,运动轨迹是半径约为60 cm 的圆周运动。图11 是陀螺质心在竖直方向上的位移随时间变化的关系曲线,坐标系的原点为绳子上端与铁架台栓系的部位,如图4 所示。由图11 可见,在竖直方向上,陀螺质心在27~38 s 比较稳定,质心在-255 mm 处的水平线上下浮动。由于绳子的疲劳和摩擦阻力等系统阻尼,导致陀螺的章动角度时刻存在微小的变化,从而使得陀螺的质心在竖直方向上颤动。

图11 陀螺质心在竖直方向上位移随时间的变化
4 结语
本文基于扭转陀螺装置,探究了陀螺的章动和进动机理,推导出了陀螺进动角速度和章动角速度的数学表达式,分析了其影响因素,并且依据实验与理论之间的对比,验证了其正确性。陀螺的运动可以分为3 个阶段:触发阶段、衰减阶段和反向阶段。触发阶段陀螺的运动是章动;衰减阶段陀螺的运动是进动和章动,在衰减阶段陀螺存在一定时间的稳态运动,即陀螺的章动角几乎不变,进动的轨迹近似等于圆周运动,但由于绳子的疲劳等系统阻尼消耗了大量的系统中的能量,使得陀螺后期的实际运动情况与理论偏差增大,最后停止运动;反向阶段陀螺进动和章动的方向发生反向改变。陀螺的自转周期随时间分段线性变化,同时根据实验结果进行了线性拟合并得出了自转周期与时间的关系式,可以估算出一定时间范围内陀螺自转的周期。

