采用激光扫描建模的筒子纱卷绕密度测量方法

周其洪， 孙宝通， 岑均豪， 占齐宸

(1. 东华大学 纺织装备教育部工程研究中心， 上海 201620； 2. 东华大学 机械工程学院， 上海 201620；3. 广州盛原成自动化科技有限公司， 广东 广州 511400)

筒子纱染色工艺中，卷绕密度是指平均卷绕密度，作为影响染色质量的重要因素之一[1-2]，其测量精准度至关重要，不同卷绕密度的筒子纱在相同条件下染色，即使目测染色均匀，但在分光光度计评定下并非匀染[3]。卷绕密度的测量精度与匀染效果具有直接联系，测量精度越高，分类染色越精准，不匀染程度越低。实际生产中若能准确测量每个筒子纱的卷绕密度，实现精准分类染色，对提高筒子纱染色质量和优品率非常重要。

当前测量卷绕密度的方法主要为人工法，通过将筒子纱理想化为几何形状，利用人工测量直径、高度等数据计算体积，获取密度[4];但筒子纱是由纱线卷绕形成[5]，表面为柔性，非理想表面，人工法测量精度较差，且测量过程依靠手工实测，劳动强度大，效率低，易出错，实际生产中仅能抽测，不适用于全部检测筒子纱，无法满足染色的高质量需求。

已有文献中，江珊等[6]提出一种通过测量筒子纱硬度估测卷绕密度的新方法。该方法可测试筒子纱各层的硬度及纱线强力，但测量方式为插入式，易对筒子纱结构造成破坏。张建新等[7-8]采用机器视觉捕捉筒子纱侧面图像，通过图像处理与数据分析获取卷绕密度，该技术属于非接触式测量，具有高效和不损伤筒子纱的优点，但该方法的测量精度十分依赖筒子纱外形，当筒子纱上端面或下端面存在内凹特征时，测量精确度将不能得到理想保证。

为研究非接触式检测在筒子纱卷绕密度测量领域的应用，并在保证测量效率满足需求的前提下，进一步提高测量精度和测量的普适性。本文以激光位移传感器组件和可编程逻辑控制器(PLC)为核心部件，设计开发了一套高精度和高效率的筒子纱数字化扫描装置，并结合数学建模等理论，提出一种基于筒子纱纱线表面轮廓精准建模计算获取卷绕密度的方法，可解决现有非接触式方法会被筒子纱表面凹凸特征影响检测精度的难题，具有较高的测量准确性。此外，本文方法测量速度快，不会损伤筒子纱，适用于生产线大批量检测，可对每个筒子纱的卷绕密度实现准确控制，有效提高染色质量和优品率，降低成本及劳动强度，且自动化的测量设备有利于智能染色工厂的发展。

1 卷绕密度检测原理与硬件组成

本文的筒子纱卷绕密度测量方法是利用数字化扫描装置分别获取筒子纱质量与扫描区域的原始点集，对原始点集降噪后，运用拟合和旋转面方程等技术，得到筒子纱的数学模型，从而计算体积，获取平均卷绕密度。

自主设计的筒子纱数字化扫描装置如图1所示。本文方法的整体测量流程如图2所示。

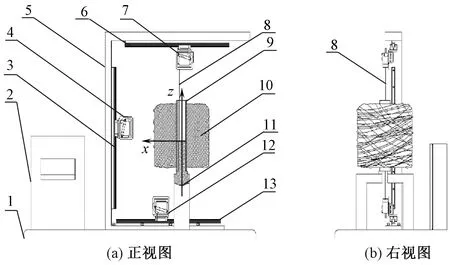
1—底座; 2—控制箱; 3—侧导轨; 4—侧面激光位移传感器(S-LDS); 5—支撑架; 6—上导轨; 7—上激光位移传感器(U-LDS); 8—激光扫描线; 9—纱筒; 10—纱线; 11—筒子纱夹具(安装有质量仪器); 12—下激光位移传感器(D-LDS); 13—下导轨。

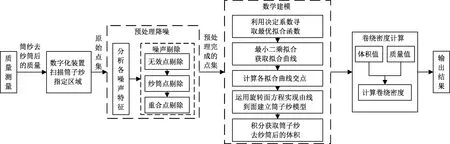
图2 筒子纱卷绕密度自动测量流程图

根据激光位移传感器(LDS)的三角测量原理，测量值M为参考位置R与测量位置P之间的位移，各LDS具有独立的测量坐标系。为方便数据的采集和后续处理，利用式(1)～(3)分别标定U-LDS、D-LDS、S-LDS，建立统一坐标系，如图1中坐标系所示。

Z=Ms-M1

(1)

式中：M1为U-LDS测量到夹具上端面中心处的测量值；Ms为U-LDS测量值；Z为将Ms转化到统一坐标系后的z轴坐标值。

Z=M2-Mx

(2)

式中：M2为D-LDS测量到夹具上端面中心处的测量值；Mx为D-LDS测量值；Z为将Mx转化到统一坐标系后的z轴坐标值。

X=Mc-M3+M4

(3)

式中：M3为S-LDS测量到夹具上端侧面时的测量值；M4为夹具上端侧面到中心轴的距离；Mc为S-LDS测量值；X为将Mc转化到统一坐标系后的x轴坐标值。

2 原始数据采集

研究所用LDS的量程为0～5 V，数字量测量值范围为-140～140 mm，A/D模块量程为0～2 000，换算公式如下：

M=VA/D×(5÷2 000)×140÷2.5-140

(4)

式中：M为数字量测量值；VA/D为A/D模块数字量。

U-LDS、S-LDS、D-LDS由控制器控制，沿导轨运动扫描，获取数据点，经式(4)换算后，得到筒子纱原始点集。为简化后续过程，原始点集偏移，保证筒子纱点集位于正z轴区域，如图3所示。图4示出图3的节选细节图，由图可分辨出纱线表面的趋向特征。

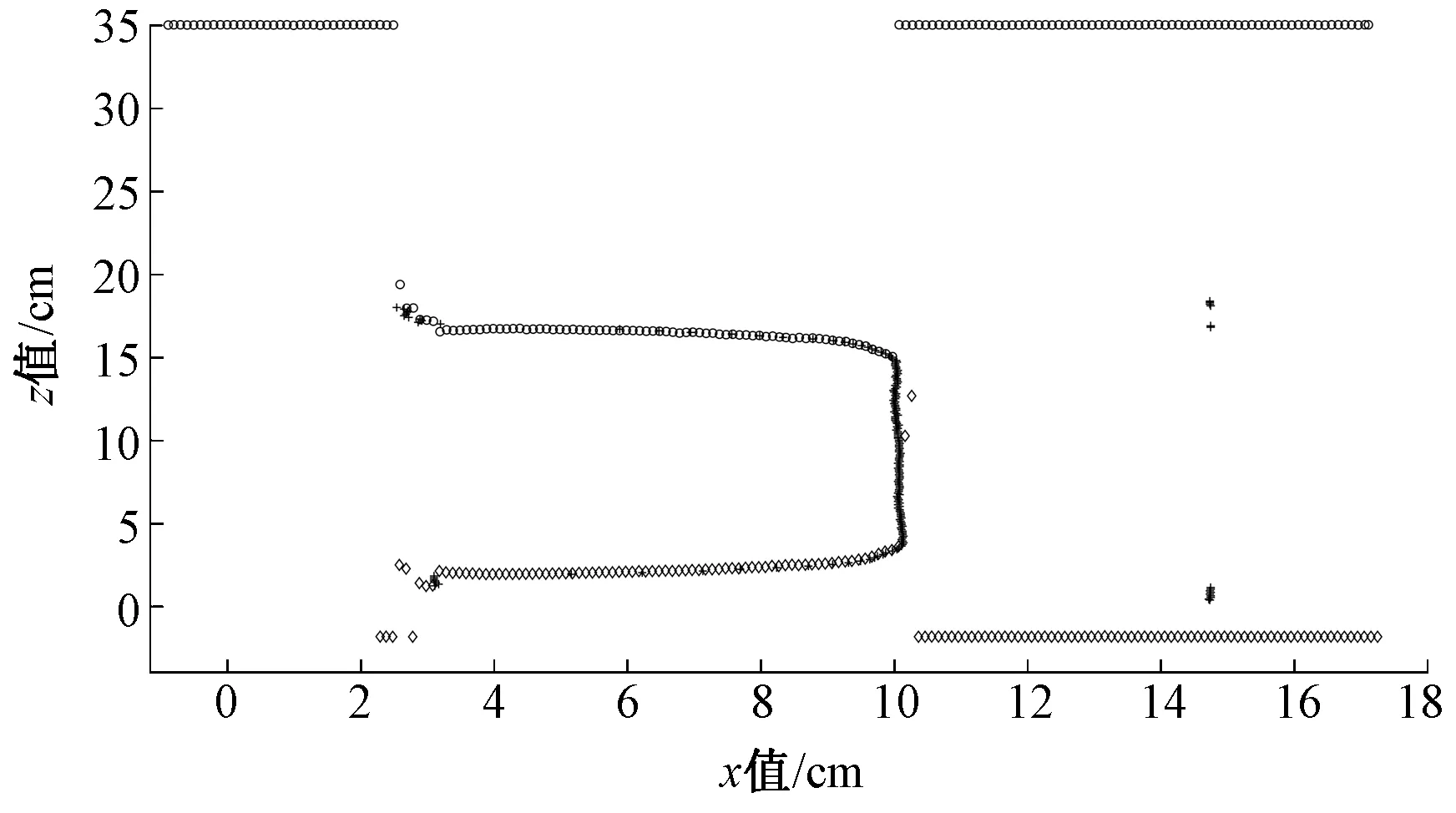
图3 原始点集总图

图3中，圆点、加点、菱点分别是U-LDS、S-LDS、D-LDS采集的数据，位于图中间区域的点集为筒子纱点集，其他呈直线趋势的点集为未检测到目标时的无效点。位于筒子纱点集左上角的圆点与加点交叉部分和左下角的菱点与加点交叉部分为纱筒点，非建模需求点。此外，原始点集是由各LDS数据拼接构建，会导致重合点问题，从图3、4中也可明显分辨出存在较多的重合点,因此无法直接利用原始点集进行数学建模获取卷绕密度，需对原始点集进行数据降噪。

3 基于特征分析的数据降噪处理

为避免无效点、纱筒点和重合点等噪声的干扰，需在数学建模计算卷绕密度前，对上述噪声分类采取方案处理。

对于无效点，该类噪声的测量值为满量程值或为特定值。本文开发设计的筒子纱数字化扫描装置的测量空间远大于LDS有效量程，故无效点为满量程值，根据此特征即可最大程度地处理无效点。

对于纱筒点，利用统计学分析数据，发现纱筒点与纱线点各存在一定的趋向规律，且二者规律相异。纱筒点的变化不稳定，连续测量值之间的差值较大，而纱线点的变化稳定在一个范围内，且纱筒点的差值变化幅度远大于纱线点的差值波动范围，该特征将纱筒点与纱线点在一定程度上分割。

根据此特征，本文提出一种利用局部特征提取配合阈值分割和条件滤波器的纱筒点剔除方法。首先计算U-LDS数据的相邻点差值，统计分析各差值出现的频数及概率，排序后获取差值的概率分布直方图，设置阈值，提取差值特征，然后根据提取的特征建立条件滤波器[9]处理纱筒点。同理其他LDS也可利用该方法处理纱筒点。

对于重合点，与处理纱筒点的思路类似，为简化计算，将S-LDS与其他LDS的重合数据视为重合点，利用约束条件式(5)进行处理。

D(Xi)=|Xi-Xi+1|

(5)

D(Xi)≥k,D(Xi+1)≤k,D(Xi+2)≤k,…,

D(Xi+j)≤k

式中：Xi为第i个对象的x值;D(Xi)为Xi与其相邻点差值的绝对值;k为约束值;Xi+j为第i+j个对象的x值。

重合点剔除思路：遍历S-LDS数据得到D(Xi)，计算概率分布图，获取D(Xi)的概率分布集中区域，然后设定约束值k建立式(5)，寻取符合条件的Xi，将其作为限界值实现重合点处理。同理，可修改约束条件的参数，处理D-LDS与S-LDS数据拼接时造成的重合点。

4 筒子纱卷绕密度计算

4.1 数学模型

数学建模的拟合方法主要为多项式拟合[10]、最小方差拟合[11]、非线性曲线拟合[12]。本文研究通过对比，发现非线性最小二乘法拟合，反映筒子纱表面趋向特征的效果更优。最小二乘法拟合法中，曲线函数φ的选取[13]至关重要。为选取最优函数φ，本文研究给出一种最优寻函算法，其原理是从函数库φ中找出拟合后的决定系数最接近1的函数φ。决定系数计算公式如下：

(6)

由于侧面点的趋向特性，存在1个x值对应多z值的问题，不符合函数定义，无法拟合出理想曲线，本文研究采用点偏移式(7)处理。

P(i)=S(i)+Q(i)×10-8,i=1,2,…,n

(7)

式中：n为侧面点的数量；S(i)为第i个侧面点的x值；Q(i)为不重复随机数序列的第i个值，Q的取值范围为[1,n]；P(i)为第i个侧面点偏移后的值。

运用最小二乘法将处理完成后的筒子纱点集分类拟合，得到拟合曲线L的函数式(8)，然后计算拟合曲线间的交点作为限界条件。

(8)

式中：aj为系数;φj(x)为关于节点xj线性无关的函数。

利用旋转面方程计算拟合曲线L的旋转曲面，得到曲面式(9)：

(9)

各旋转曲面组合即为筒子纱的纱线表面轮廓，数学建模完成。

4.2 筒子纱体积和卷绕密度计算

通过数学模型可得到：拟合曲线L1(上)、L2(右)、L3(下)、L4(左)，曲面A1、A2、A3、A4和交点a(L4与L1)、b(L1与L2)、c(L2与L3)、d(L3与L4)。

将上述参数引入柱坐标三重积分公式，计算筒子纱纱线体积V，积分式如式(10)所示。应用式(11)获取筒子纱的平均卷绕密度ρ。

(10)

(11)

式中：G为筒子纱质量，g；m为纱筒质量，g；θ为方位角，(°);r为径向距离，cm。

5 实验验证及分析

本文实验平台为MatLab2019b，实验环境为Windows10 x64位计算机系统。LDS的扫描范围0～180 mm，取样间隔为1 mm。扫描样品如图5所示。样品a外形特征差，质量为1 590 g，平均直径为205 mm，筒子直径为66 mm，筒子质量为124 g，纱线部分平均高度为148 mm；样品b外形特征好，质量为1 584 g，平均直径为188 mm，筒子直径为66 mm，筒子质量为124 g，纱线部分平均高度为157 mm。

图5 样品示意图

5.1 计算与对比实验

以样品a为实验对象，首先剔除原始点集中的无效点，得到筒子纱点集，截取筒子纱点集中噪声点与建模点交界位置的数据，如表1所示。其中：U-LDS、D-LDS中需处理的数据为纱筒点，有效数据为纱线点，S-LDS中需处理数据为重合点。

利用纱筒点处理方法得到的U-LDS原始概率直方图如图6(a)所示，阈值分割提取到的差值特征如图6(b)所示。由表1可知U-LDS纱线点的差值变化范围在-0.042～0.07 cm间，证明利用差值特征提取方法可有效确定纱线点的变化范围。同理，可得D-LDS的差值特征。

运用本文的重合点剔除思路，获取的S-LDS差值概率集中区域为：0～0.048 cm，与表1数据一致，证明剔除思路有效，设定约束条件式(5)的参数为k=0.048 cm，j=6。

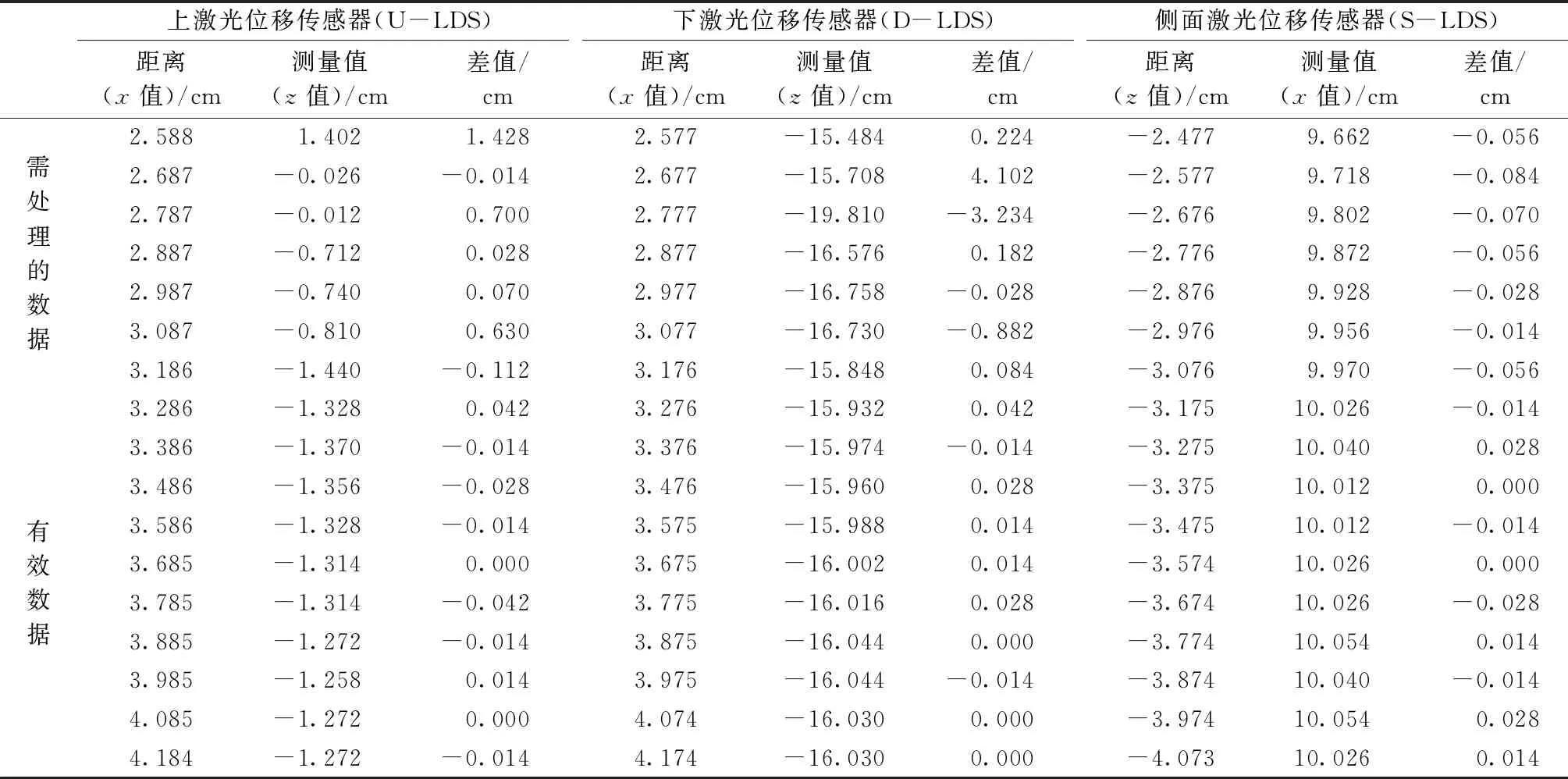
表1 原始点集中纱筒点、重合点与建模点交界处的数据

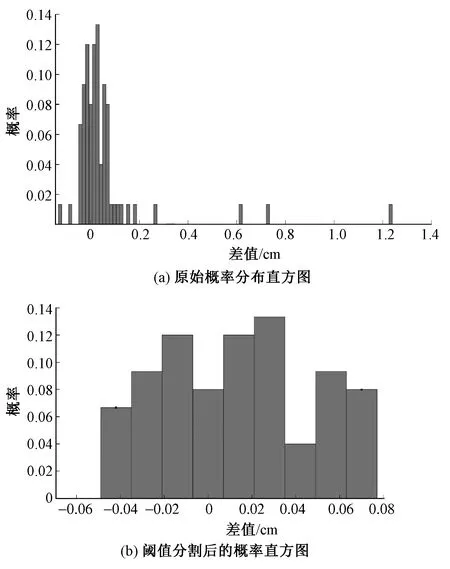
图6 差值的概率分布直方图

以差值特征建立条件滤波器剔除纱筒点，利用约束条件式(5)寻取限界值剔除重合点。完成数据降噪处理后的点集如图7(a)所示。分类应用最优寻函算法搜寻最优函数，完成非线性最小二乘法拟合，拟合后的曲线如图7(b)所示。其中：L1的最优函数为7次多项式，R2为0.995 8，Sres为0.033 6；根据侧面点特征，L2采用直线函数完成最小二乘法拟合；L3的最优函数为8次多项式，R2为0.998 6,Sres为0.012 3；L4为纱筒与纱线的交界线，由纱线上端点与下端点的初始点拟合。

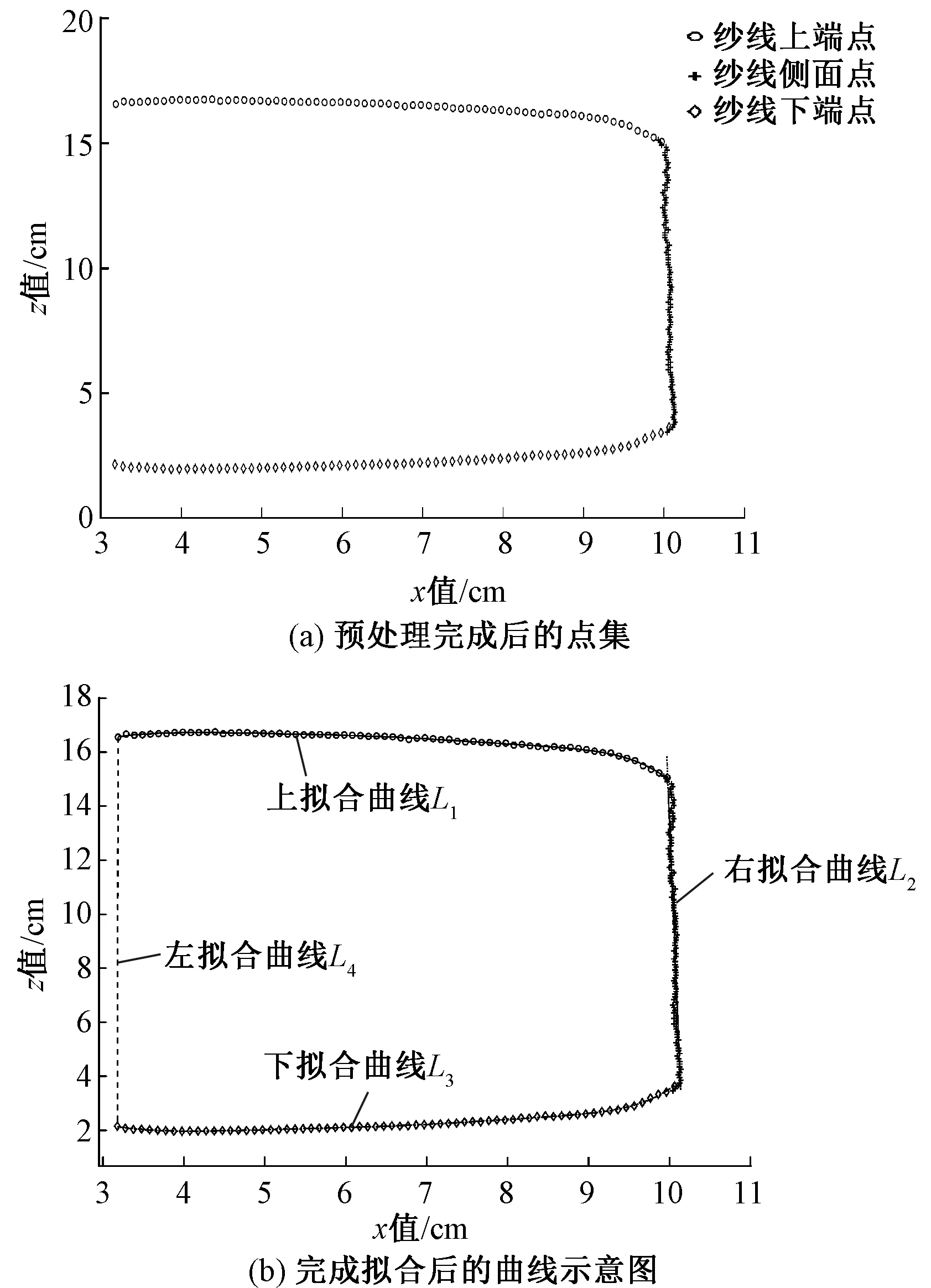
图7 建模示意图

计算交点，并对L1、L2、L3、L4运用旋转面方程，得到曲面A1、A2、A3、A4，然后利用式(10)和式(11)计算样品a的卷绕密度为3.687×10-1g/cm3。

为验证该方法的有效性和准确性，应用本文方法与行业通用人工法对同批样品进行对比测量实验。其中测量效果最差与最优的2组实验数据如表2所示。样品外形如图5所示。可看出，本文方法相比于人工法而言，测量精度明显提升，且筒子纱外形特征越好测量精度越高，即使筒子纱外形特征很差，本文方法也能将相对误差控制在2.5%内。主要原因是：本文方法将筒子纱纱线表面真实的纹理趋向和凹凸状态考虑在内，利用数学语言准确表达其外形特征实现测量。

表2 行业方法与本文方法的实验对比结果

实验中，本文研究的测量时间都能控制在8 s内，其中测量程序耗时在0.75 s内，剩余时间由硬件扫描浪费，故提高硬件的扫描速度可进一步提高效率。而人工法的测量时间至少在80～120 s。2种方法差异较大的原因为：当前行业通用方法测量过程依赖人工，测量结果好坏和测量时间长短完全取决于工作人员的熟练水平和经验，本文方法的测量则是通过设计开发的装置自动完成，具有较高的自动化水平，尤其是在大批量生产时，生产效率更为突出。

5.2 重复性验证实验

为验证本文研究方法测量的稳定性，对实验样品进行多次重复测量，随机取10次测量数据如表3所示。应用Bessel公式[14-15]计算标准偏差为S=0.069%，结果证明测量十分稳定，具有理想的重复精度，实际生产中通过补偿等方法可使最终的测量精度达到理想要求。

表3 同一样品的重复测量数据

6 结 论

本文给出了一种精度高、速度快、成本低的非接触式筒子纱卷绕密度自动测量方法，利用自主设计和搭建的筒子纱数字化扫描装置获取原始数据，基于噪声特征实现原始数据的降噪处理，利用最小二乘法拟合与旋转面方程建立筒子纱去纱筒后的数学模型，配合积分法得到体积值，并与测得的质量值结合，计算出筒子纱的平均卷绕密度。实验证明，本文方法的测量相对误差不超过2.5%，测量程序耗时小于0.75 s，重复测量的标准偏差为0.069%，具有优秀的测量精度和稳定性，可有效满足生产需求，为非接触式检测在卷绕密度测量领域的发展，提供了一种新的方法，同时自动化的测量方法和设备十分有利于数字化管控。