长输卤水管道泄漏检测与定位技术研究
肖 峻,高东俊,奚修豪
(武汉理工大学 机电工程学院,湖北 武汉 430070)
盐卤是制作豆腐的关键成分,也是工业中提取生产卤素的重要原料。卤水具有强腐蚀性,且在运输过程中温度较高,使得盐卤泄漏不仅会对环境造成严重污染,还会给人们带来巨大的经济损失[1],故需要采用有效的方法对卤水管道泄漏进行及时检测和准确定位,从而使经济损失和环境污染最小化。随着新兴技术的涌入,如压力变送器技术[2]、光纤技术[3-4]、声波法[5]、小波变换技术[6]、经验模态分解[7-8]等,负压波法的定位精度与泄漏检测准确率得到提升[9]。为此,笔者采用改进的小波阈值消噪算法对采集的压力信号消噪,基于极值的方法获取压力突变时间标签点,并通过优化的定位算法进行定位计算,以期提高卤水管道泄漏检测与定位效果。
1 负压波检测原理
由于负压波频率较低,在管道内的反射衰减速度较慢,所以负压波可沿管道两端传播很远的距离[10]。当负压波到达管道两端时,会出现一段时间压力陡降,这时可通过负压波到达管道两端的时间差和负压波在管道中的传播速度来确定泄漏点的位置,故可在管道两端分别布置压力传感器,采集负压波信号。负压波检测原理如图1所示。
负压波泄露点定位包括负压波到达管道两端传感器的时间差和负压波波速两个关键因素,泄漏点定位公式为:
(1)
式中:x为泄漏点到管道首端的距离;L为管道长度;α为负压波传播速度;V为管道内流体流速;Δt为泄漏所产生的负压波传到管道首、末两端的时间差。
2 负压波波速计算
2.1 负压波波速通用计算公式
负压波的传播速度随着管道物理参数、传输介质物理性质及外界物理参数的变化而具有不同的表现形式,此处考虑纯液中负压波的传播速度,根据质量守恒、液体的连续性和液体压缩与管壁膨胀原理,负压波传播速度可表示为[11]:
(2)
式中:α为负压波传播速度;ρ为管道液体密度;K为管道液体体积模量;E为管道材料的弹性模量;D为管道的平均内径;δ为管道的管壁厚度;ψ为管道修正系数。
2.2 负压波波速公式修正
在实际工程中,温度是影响负压波传播速度的首要物理因素,液体密度和液体体积模量都会随温度变化而变化。由于卤水的粘度较小,在管道内的流动性好,所以温度在卤水管道中传播比较均匀。通过采集现场的卤水,将卤水加热到不同温度并对其密度进行测量,得到不同温度下的卤水密度,并对其进行线性拟合。其中,温度在65~74 ℃范围内卤水密度与温度的关系如图2所示。
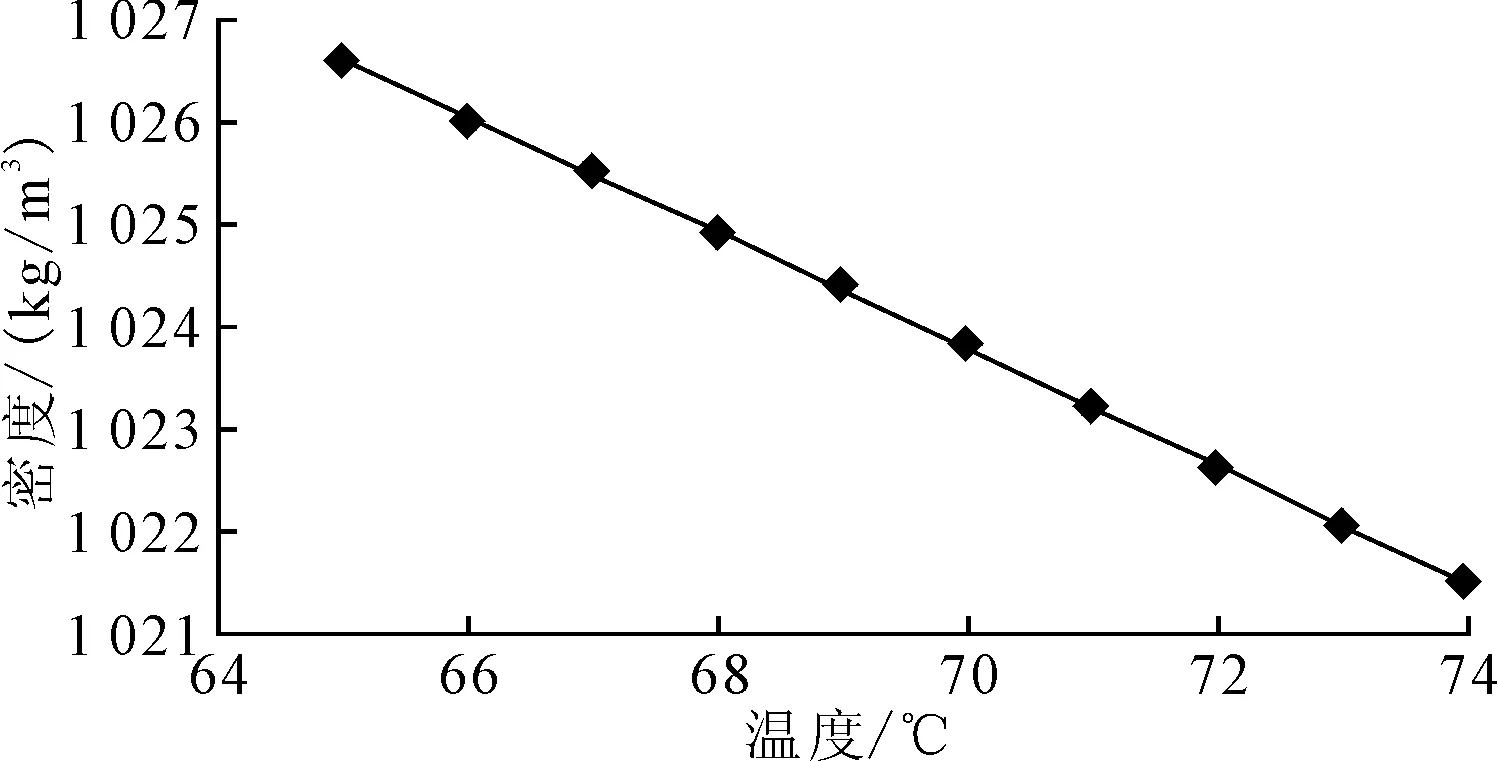
图2 卤水密度与温度的关系
进一步得到卤水密度与距离的表达式为:
(3)
式中:x为泄漏点到管道首端的距离;τ1、τ2分别为管道首端与末端的温度测量值;L为管道长度。
现场测得卤水矿化度为10 g/L,根据文献[12]中同矿化度卤水在不同温度下体积模量的测量数据,得到体积模量与距离的表达式为:
(4)
从而得到修正后的负压波传播速度:
(5)
3 压力信号消噪
3.1 消噪算法优化
小波软阈值消噪算法处理后的信号具有很好的连续性,但处理后的小波系数与原小波系数之间存在一定偏差,会给重构后的信号带来误差[13-14]。为此,采用指数型阈值函数对阈值函数进行优化,其表达式如式(6)所示。
(6)

以Bumps加噪信号为例进行消噪仿真分析,软阈值消噪算法与指数型阈值函数消噪算法相关性能指标对比如表1所示,消噪效果对比图如图3所示,结合表1和图3可知,指数型阈值函数消噪算法整体降噪效果较好,且在较关键的最大突变段起始点与终止点处波形特征体现更好,便于后期读取时间标签点。
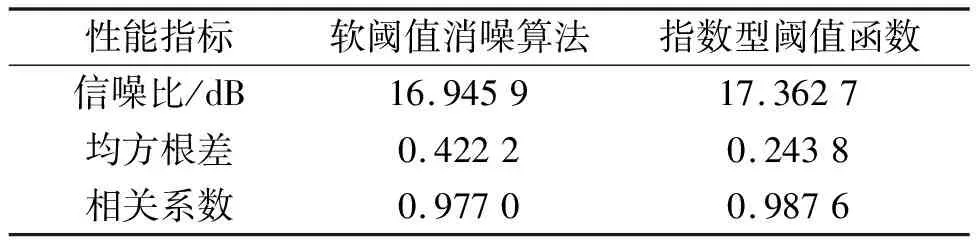
表1 软阈值消噪算法与指数型阈值函数消噪算法性能对比

图3 消噪对比图
3.2 时间标签点的读取
在已消噪的压力信号基础上读取负压波中幅值变化最大的陡降段的首、末两个极值点,并将其作为时间标签点,原因在于负压波在传播至管道首、末两端压力传感器过程中会衰减,但衰减主要体现在幅值上,其频率变化较小,整个波形的时间标签点相对固定。为了得到更准确的泄漏时间差,可将管道首、末两端压力传感器所检测到的压力最大突变段起始点与结束点作为时间标签点,根据实验数据进行采样点的截取,确定时间标签点,具体如图4所示。
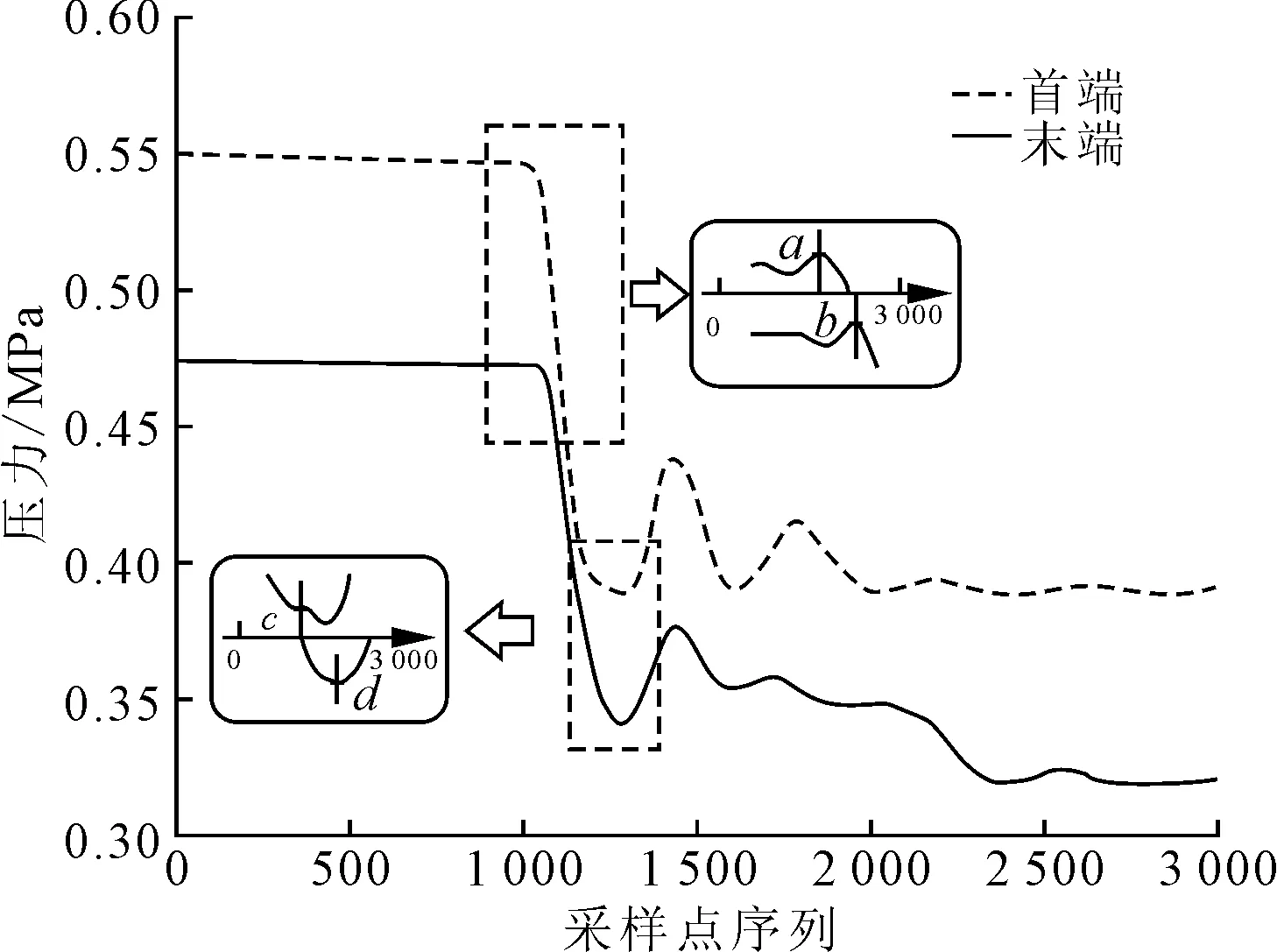
图4 时间标签点读取示意图
图4中,a、b分别表示管道首、末两端圧力曲线的最大突变起始点,c、d分别表示管道首、末两端圧力曲线的最大突变结束点。则泄漏时间差的计算公式为:
(7)
式中:n1、n2、n3、n4分别为a、b、c、d4个点所对应的采样点序列数;f为系统采样率。
4 泄漏点的定位计算
4.1 泄漏点定位算法
根据式(5),某次泄漏所产生的负压波传播到管道首、末两端所用时间分别为:
(8)
式中:t1和t2分别为负压波传播到首、末两端的时间;xlack为泄漏点坐标。
笔者采用Romberg算法计算数值积分,以t1的数值积分为例,首先将积分区间[0,xlack]分成n等份。设x0=0,xn=xlack,则有:
xk=kh
(9)

(10)
将步长减半,得到积分域2n等份后的近似值为:
(11)
于是可以得到递推公式为:
(12)
故由截断误差表达式可得:
(13)
式中:RTn(α)、RT2n(α)分别为选取步长h、h/2计算得出的截断误差;I(α)为负压波由泄漏点传递至管道首端的实际时间;Tn、T2n分别为选取步长h、h/2计算得出的负压波由泄漏点传递至管道首端的时间。
虽然在管路中负压波传播速度随位置不同而发生变化,但波速关于位置的二阶导数相对变化不大,故α″(ξ1)≈α″(ξ2)。由式(13)可得:
(14)
(15)
由于α(x)关于x的四阶导数和六阶导数变化不大,可通过Simpson值、Cotes值到Romberg值的迭代计算,加速收敛求解过程,3个值的计算方法如式(16)所示。若精度要求为ε,则当|R2n-Rn|≤ε时,可达到精度要求。
(16)
4.2 算法优化
虽然通过Romberg算法对上、下变积分的计算更准确,但其搜索范围较广泛,故首先压缩搜索范围,然后进行区间二分搜索。
4.2.1 压缩搜索范围
假定管路中波速为常数值,将首、末两端计算所得波速α(0)、α(L)代入式(1)进行计算,得到泄漏点分别为xf、xe。由于α(x)为单调递减函数,所以实际泄漏点应在(xf,xe)区间内。
4.2.2 区间二分搜索
在(xf,xe)区间内,根据1/2比例对搜索范围进行不断压缩。每一次代入的位置计算点为上一次搜索所确定区间的中点,并由新的搜索点来判断下一次的搜索区间。区间二分搜索示意图如图5所示。将xi(xi∈(xf,xe),i=1,2,…,m)代入到Romberg算法中计算近似时间值t1和t2,求得时间差为Δti,进一步求得Δti与实测时间差Δt的差值。
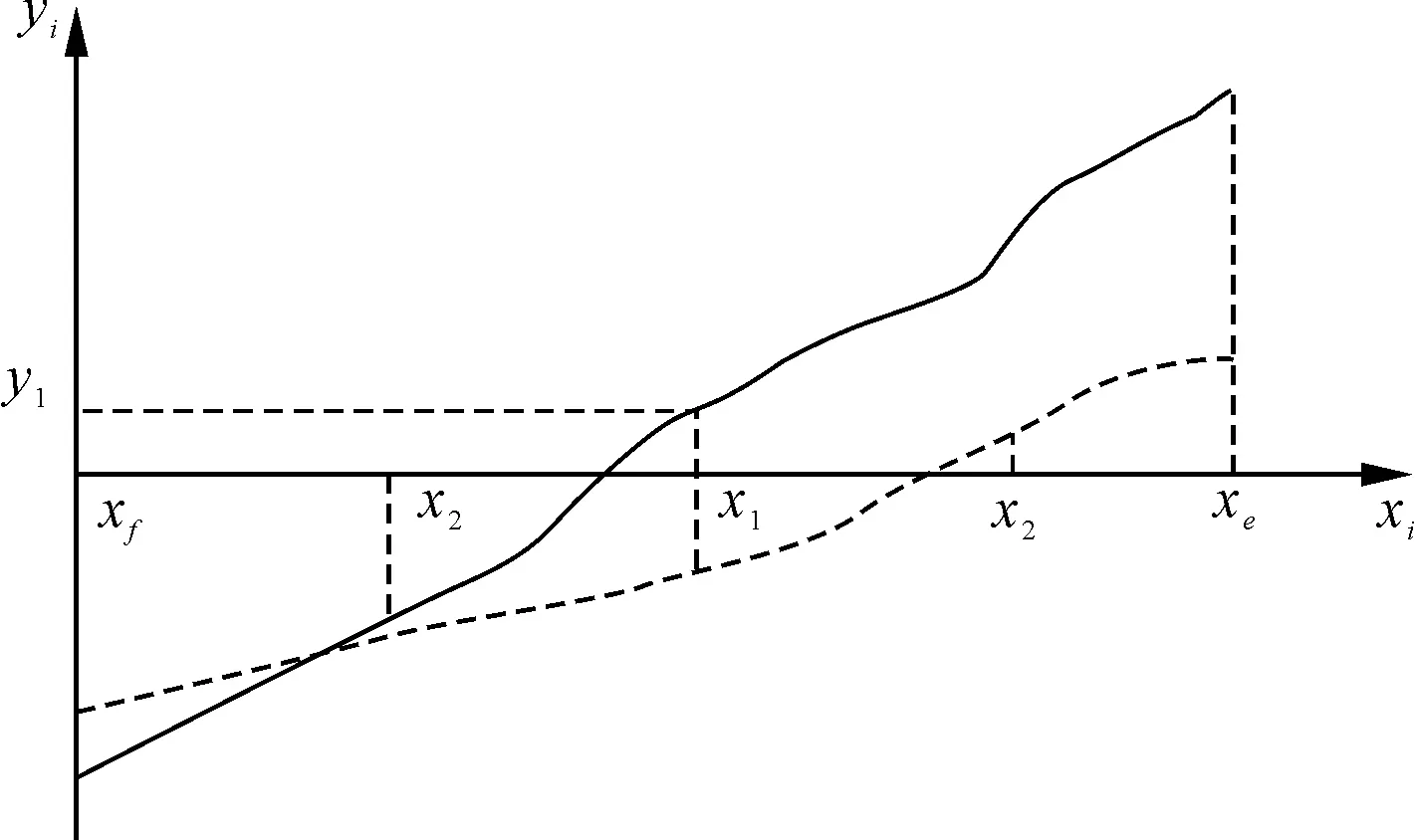
图5 区间二分搜索示意图
以点x2为例,取x1=(xf+xe)/2,可得到y(x1)的值,然后比较y(x1)、y(xf)的大小。若y(xf)×y(xe)<0且y(xe)×y(x1)>0,则舍去(x1,xe)段,再对(xf,x1)区间进行二分搜索,如图5实线所示,取x2=(xf+x1)/2为下一次二分搜索点。若y(xf)×y(x1)>0且y(xe)×y(x1)>0,则舍去(xf,x1)段,再对(x1,xe)区间进行二分搜索,如图5虚线所示,下一次区间二分搜索点为x2=(xe+x1)/2。按照上述方法不断进行二分搜索,直到搜索区间的宽度小于或等于设定阈值δ,取最小搜索区间的中点为最终定位点。
4.3 定位算法实现与性能分析
运用Matlab对优化后的Romberg算法编程,泄漏点定位计算流程图如图6所示。假设管道长度L=20 km、时间差Δt=15 s,波速表达式相同,定位精度分别为1%和5%的情况,进行100次仿真实验,得到定位计算耗时情况如表2所示,可看出两种定位精度的算法耗时基本相同,对泄漏点的定位计算实时性影响不大,故选取定位精度为1%进行定位计算。

表2 定位耗时比较

图6 泄漏点定位计算流程图
5 实验与结果
5.1 实验检测装置
为了验证上述方法的可行性,在室外环境下搭建模拟卤水管道泄漏检测与定位试验平台,选取管径D为20 mm、壁厚δ为1 mm的薄壁管道,实验中所使用液体为工业盐溶解液,管道压力范围为0~0.8 MPa,通过开关球阀来模拟泄漏。管道结构设置为U型,设定两压力传感器间管道总长度为33.25 m,两球阀的安装位置与首端压力传感器的距离分别为12.00 m和21.25 m。实验采用STM32单片机和Matlab软件平台对压力信号进行采集和分析,具体如图7所示。

图7 室外模拟实验平台
5.2 实验结果与分析
实验选取泄漏点为12.00 m和21.25 m的数据进行分析和计算,现场采集的压力信号与消噪情况如图8所示,泄漏定位结果如表3所示。结合图8和表3可以看出,压力信号消噪效果良好,泄漏点的定位精度较高。

图8 压力信号消噪情况

表3 泄漏定位结果
6 结论
利用负压波法可以对长直输卤管道进行泄漏点检测和定位。笔者通过对卤水密度与温度关系的标定,修正了负压波波速计算公式,减少了温度对波速的影响。采用小波阈值消噪算法对采集数据进行滤波,有效降低了噪声干扰,有助于拾取压力突变点。选取Romberg积分算法进行定位计算,大幅提高了计算准确度。实验结果表明,上述研究方法能有效提高卤水管道泄漏检测和定位效果。

