舰炮射击命中概率最低可接受值的确定∗

（92941部队43分队 葫芦岛 125000）

1 引言

舰炮武器试验受经费等条件限制，射击试验用弹较少，传统试验理论难以满足试验、评定要求，因而研究新的评定方法有着重要的意义。在舰炮武器射击试验二项分布假设检验中，备择假设H0:p=p0、H1:p=p1中，p1的确定非常重要，但选取时却没有确定的方法，给试验设计带来一定的困难。本文利用中心极限定理，构造正态分布统计，建立射击弹数、军方风险与验证指标之间的关系，提出了命中概率最低可接受值的确定方法，为试验方案提供依据。

2 最低可接受值 p1的确定

p1是军方最低可接受值，p1=f(p0，n，α)，其中，p0为设计值，n为试验样本数，α为生产方风险。

p1与p0的关系为，随着样本数的增大，p1逐渐接近p0。

p1的大小与军方风险β有直接关系，在一个试验方案中，若生产方风险α增大，军方风险β就会减小，反之亦然，试验风险由双方共同承担，因此为保持公平原则，工程实践中多采用双方等风险原则。

对于二项分布参数的假设检验：

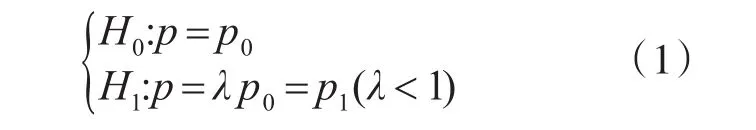
用x{n}表示一组服从二项分布的样本，对于任何随机变量xk（k=1，2，…，n）。

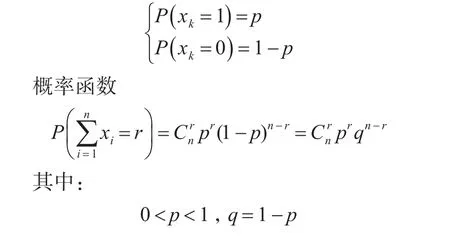
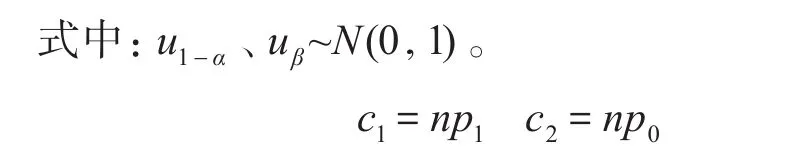
上式可分解为如下两个表达式：

式中：Z1-α、Zβ为对应标准正态分布的上分位点，它的值可从正态分布分位数表中查取。

而上式中，p1=f(p0，n，α)的表达式满足上面关于p1选取的讨论，则

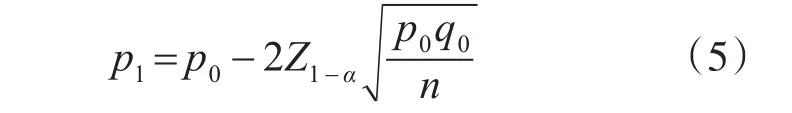
可参考上述表达式确定最低可接受值的大小。

3 试验方案

在舰炮武器试验中，如试验样本量n受限，则可利用本文最低可接受值的确定方法制定试验方案。例如，命中概率指标按目标面积1000m2×1000m2区域落入概率为0.5和0.2625分别计算，可得最低可接受值p1如表1。

表1 军方最低可接受值p1

4 结语

在舰炮武器系统试验中，二项分布假设检验最低可接受值p1的确定，可以有效降低军方风险，减少试验次数，缩短检验周期，节省经费，提高试验质量和效益。