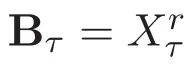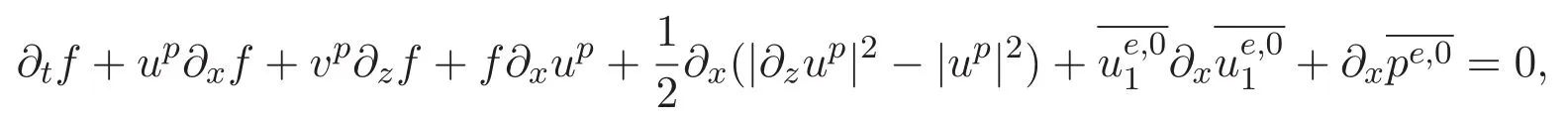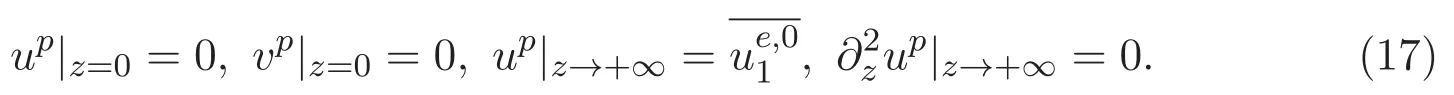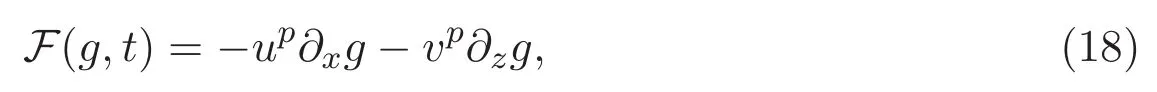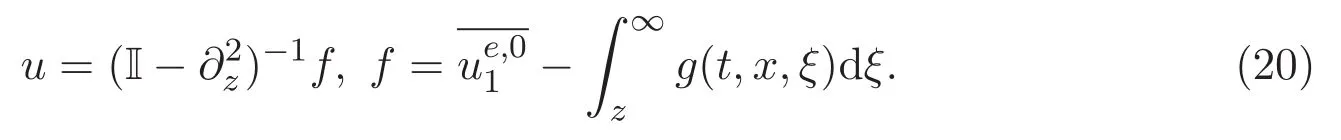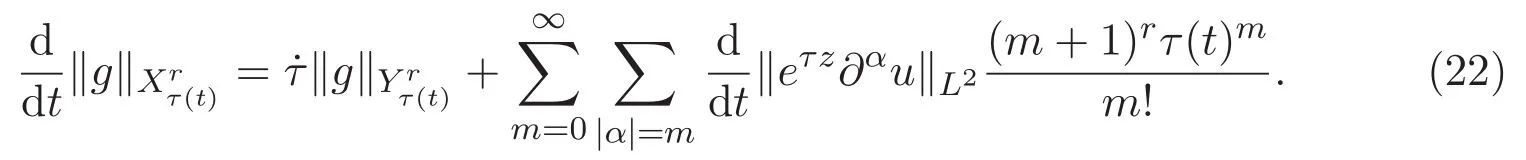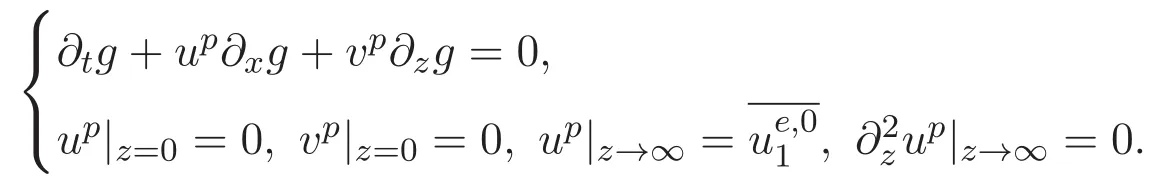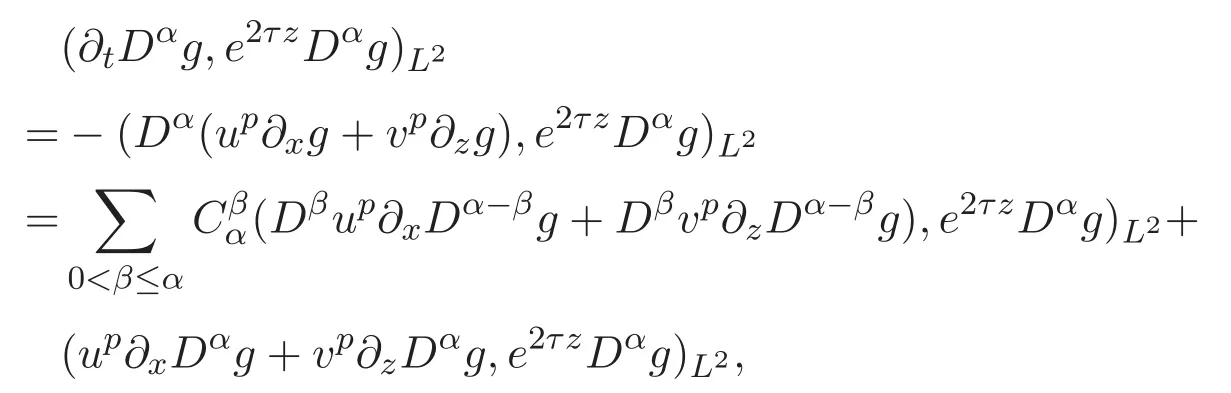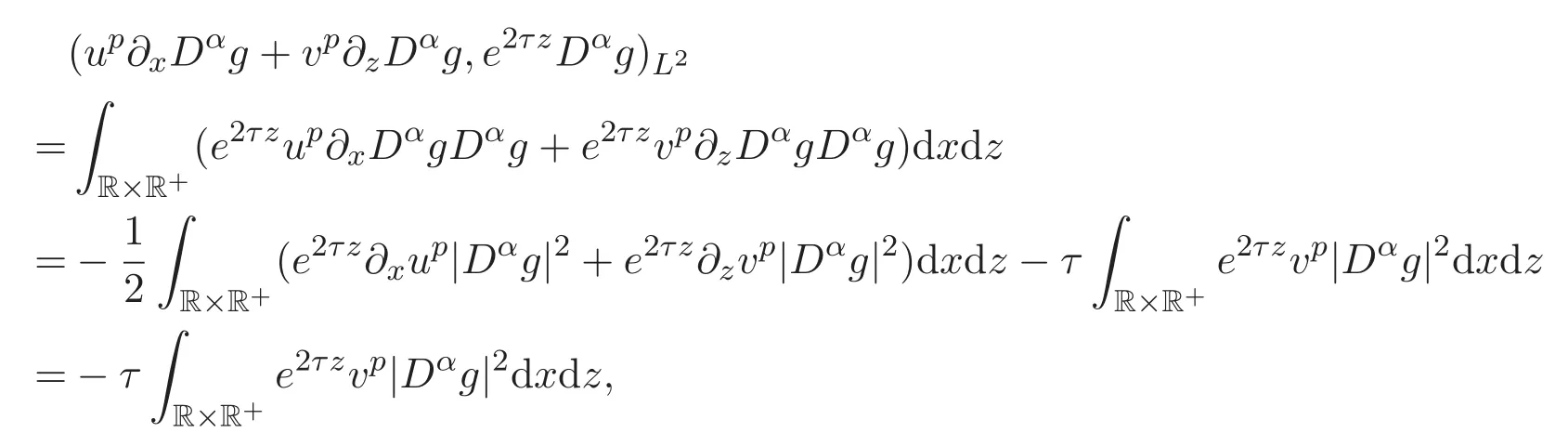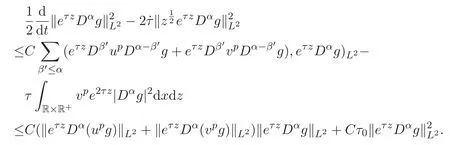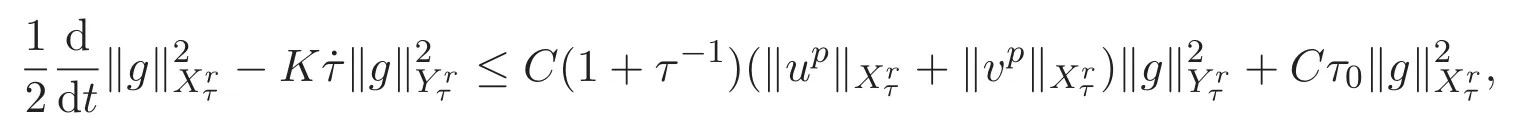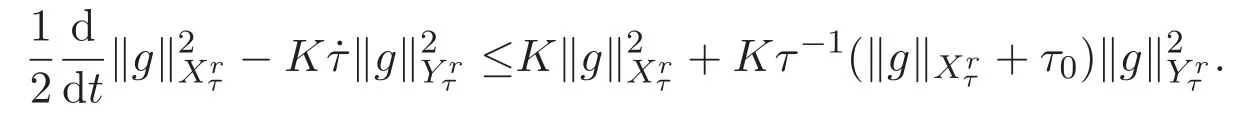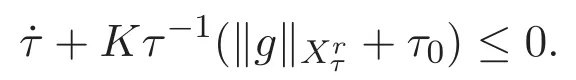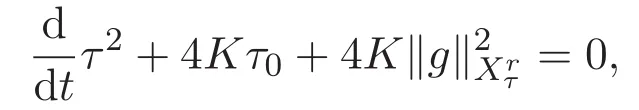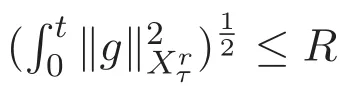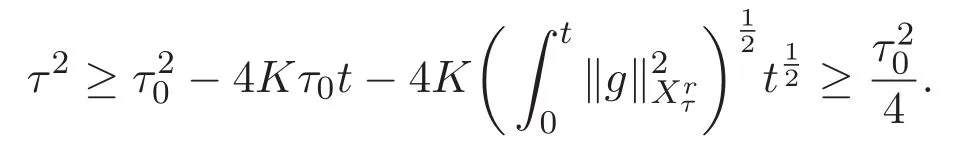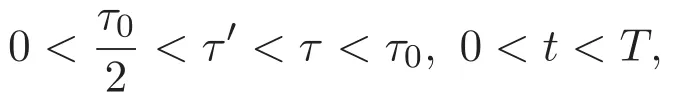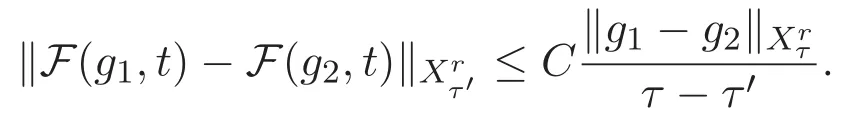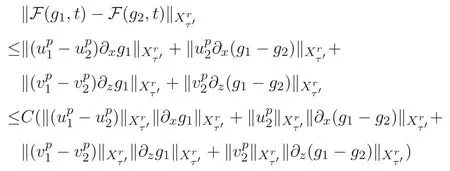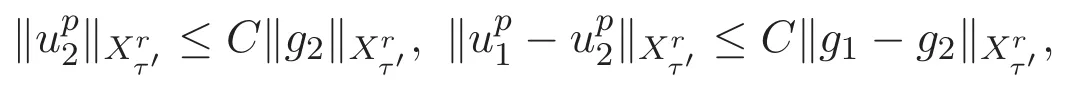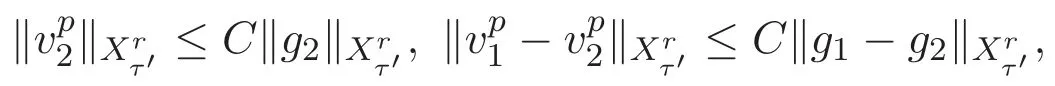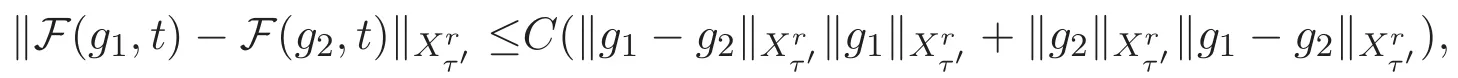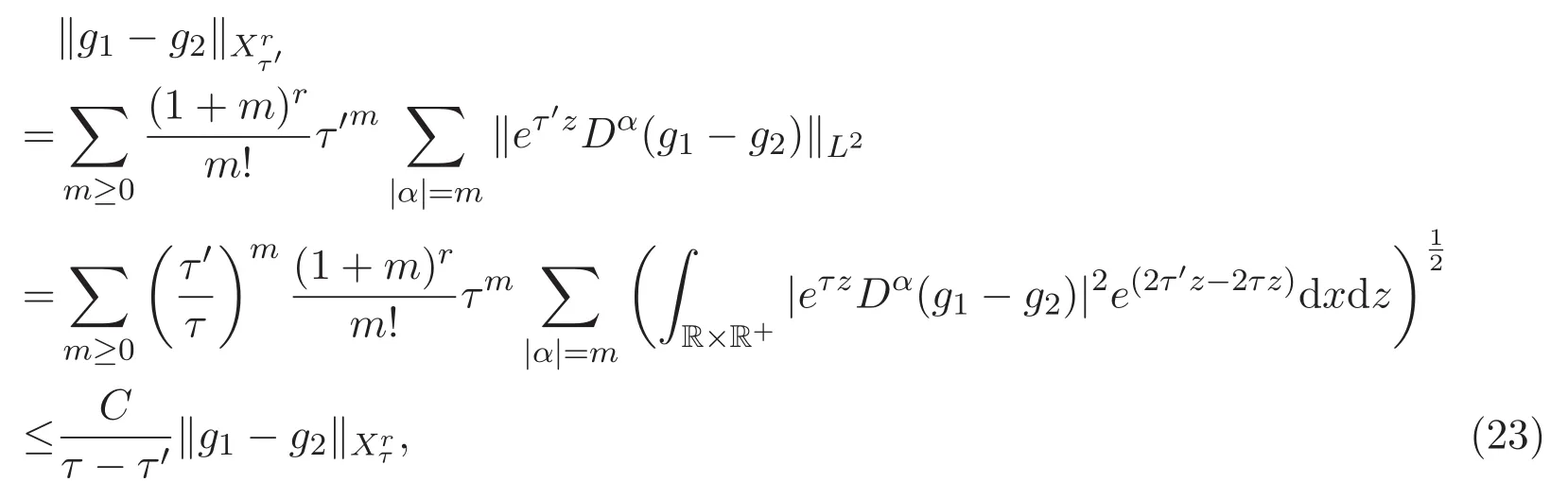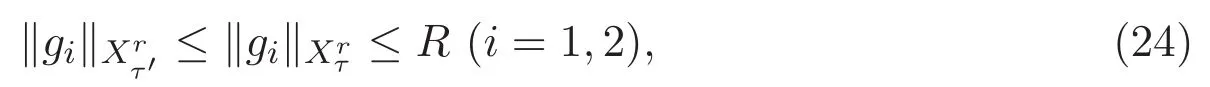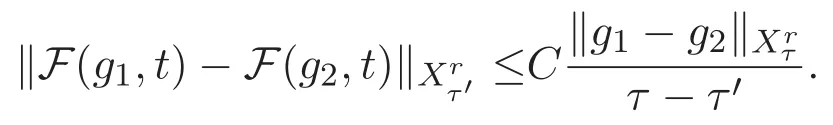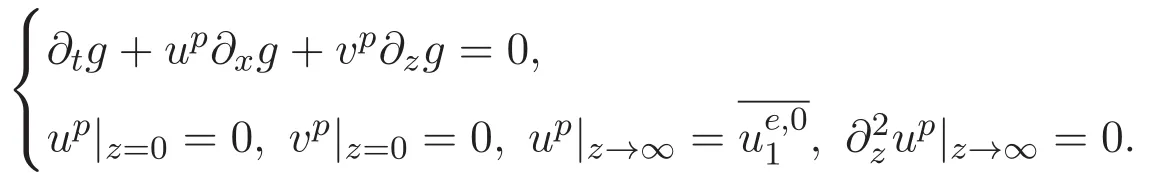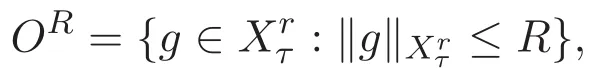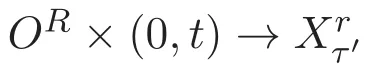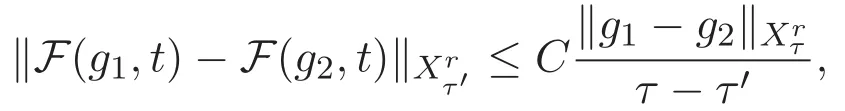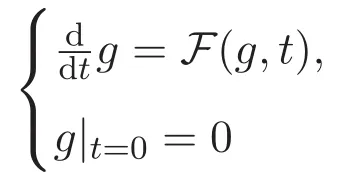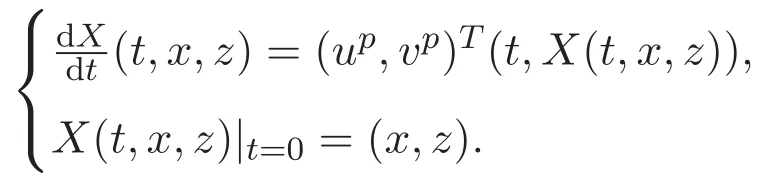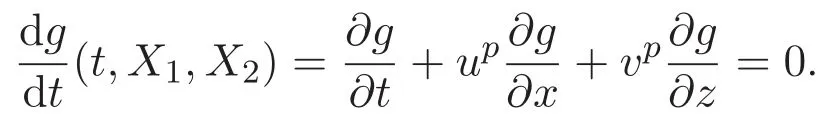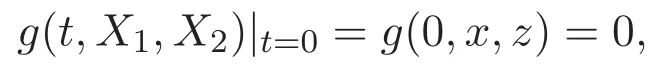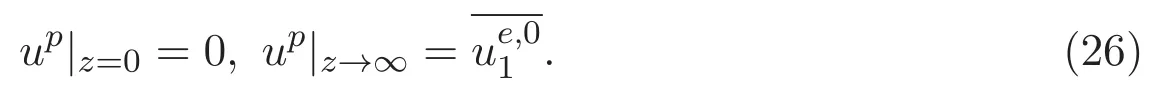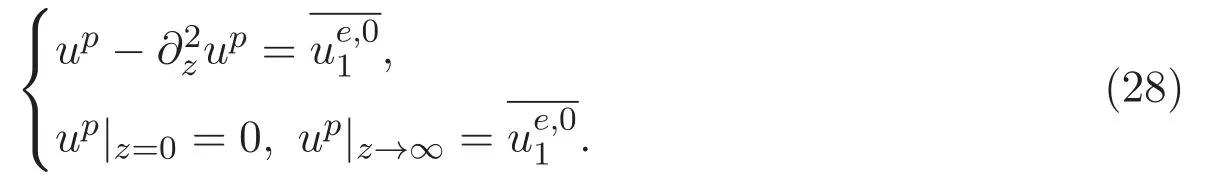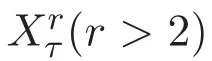半平面上Euler-α方程组的边界层方程整体适定性
孙小梅,臧爱彬
(1.西北大学数学学院,陕西 西安 710127)
(2.宜春学院数学与计算机科学学院和宜春学院应用数学研究中心,江西 宜春 336000)
1 引言
在半平面上具有Dirichlet边界条件的Euler-α方程组有如下描述
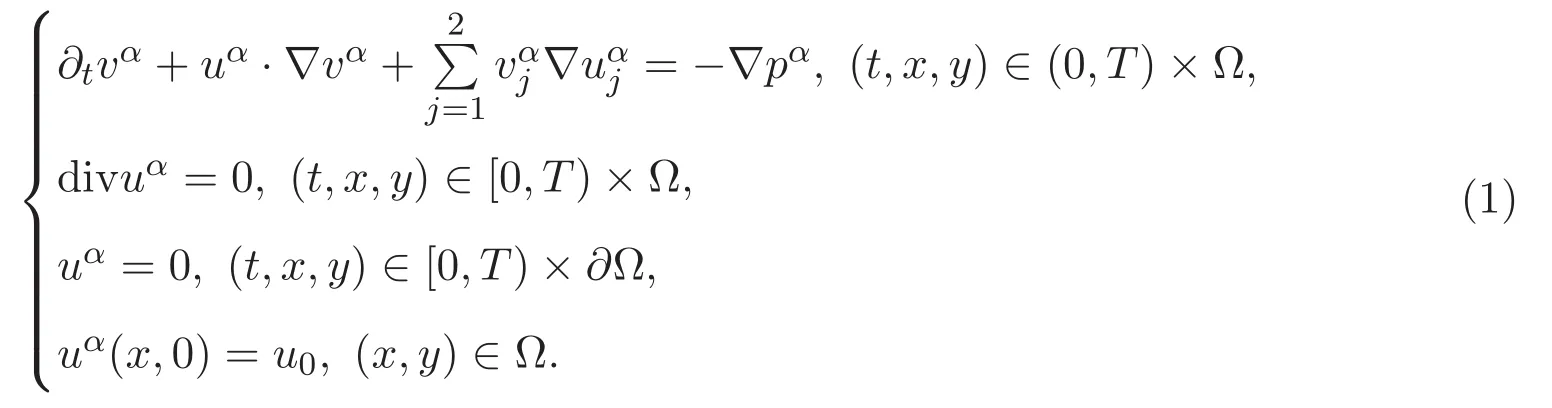
文献 [2]通过使用几何工具证明了初始值u0∈Hs(Ω)(s>2)时问题 (1)的存在唯一性.文献[3]用描述粒子演化的唯一拉格朗日流图证明了Radon测度空间中具有初始涡量的二维Euler-α方程组整体弱解的存在唯一性.对于足够光滑的初始数据,文献[4]证明了Euler-α方程组存在唯一局部强解,并证明了二维情况下Euler-α方程组具有整体唯一强解.
形式上,令方程组(1)中的参数α=0,可以得到Euler方程组的初边值问题
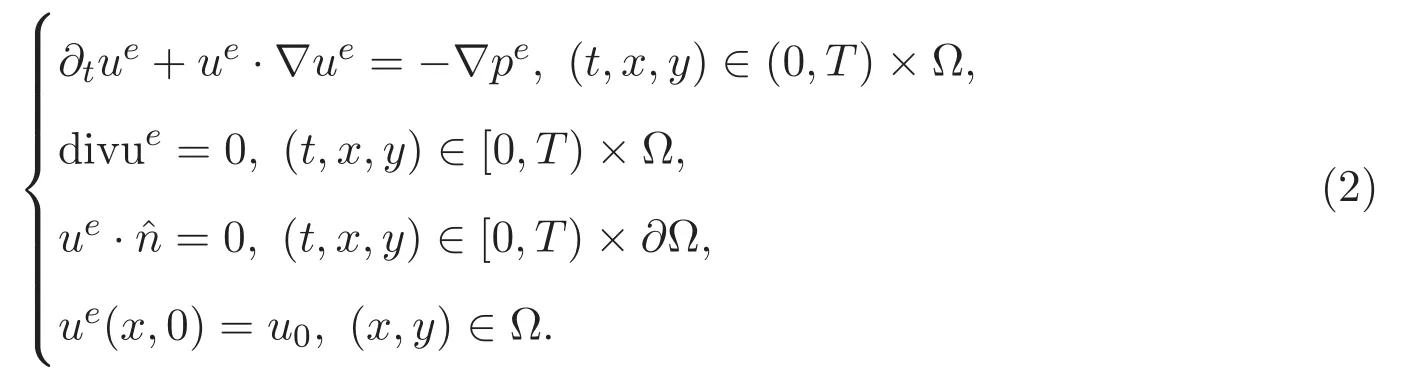
对于Euler方程组的适定性已经有了广泛的研究,文献[5]证明了n维区域内Euler方程组(2)经典解的局部存在唯一性,而在二维情形下该解还是整体存在的,更多细节读者可参考文献[6].
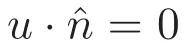
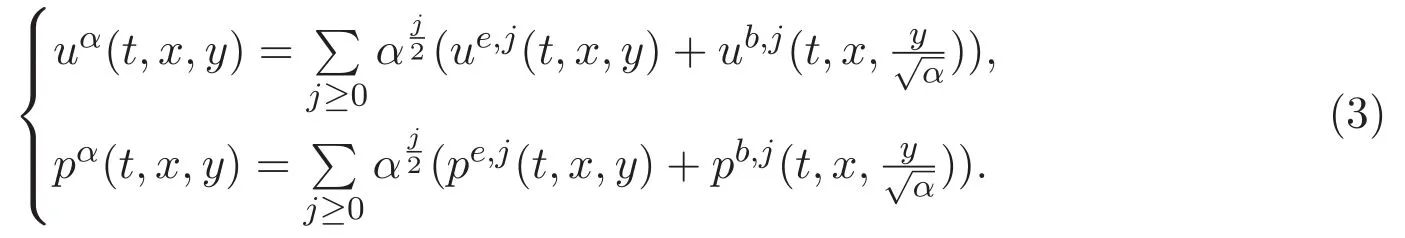
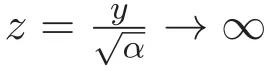
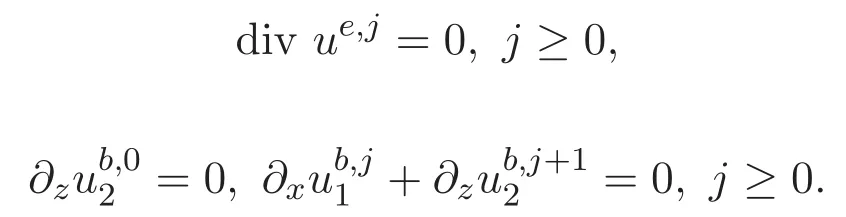
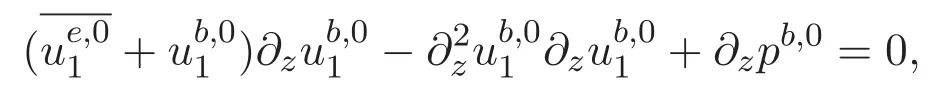
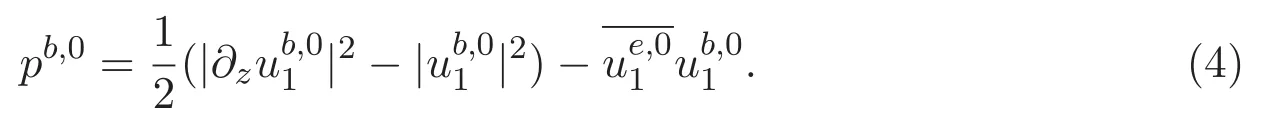
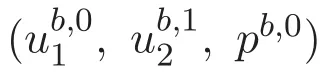
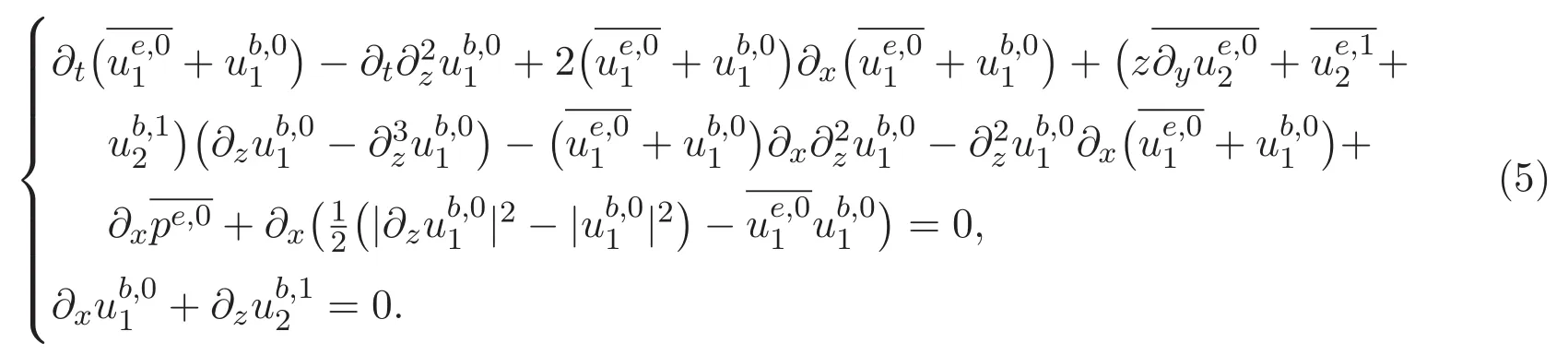
以及边界条件
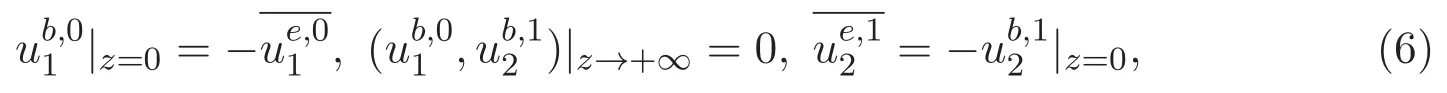
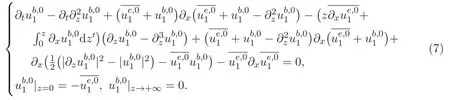
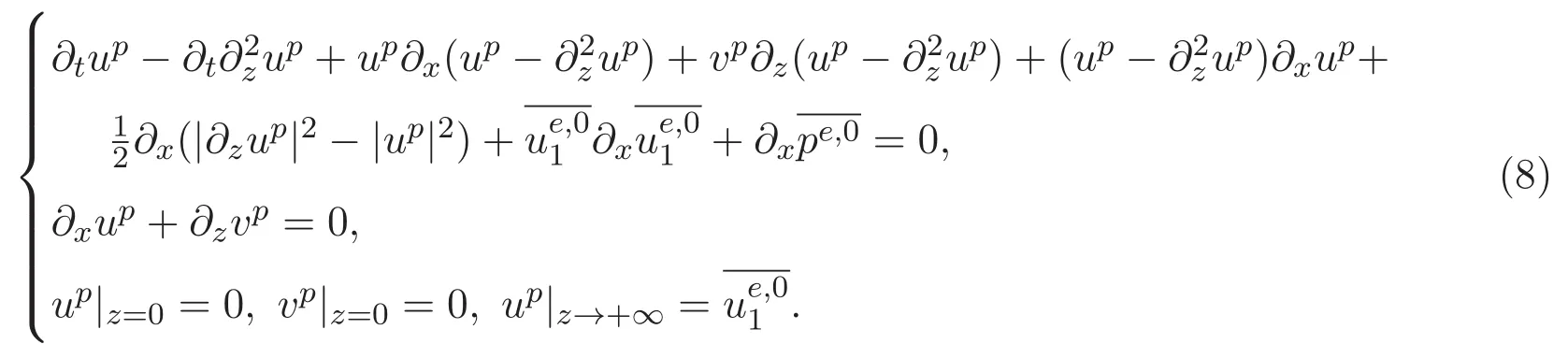
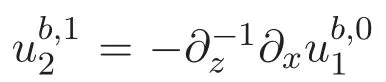
本文的主要内容结构如下:第二部分给出了加权Lebesgue-Sobolev函数空间以及解析函数空间族的定义及性质.简述了ACK定理的内容和证明一些有用的命题.最后部分通过构造边界层方程组的等价形式,引入了两个技术性的引理,从而给出本文的主要结论及证明.
2 符号及预备知识
为方便起见,对于正数r,τ>0,定义以下的加权Lebesgue函数空间
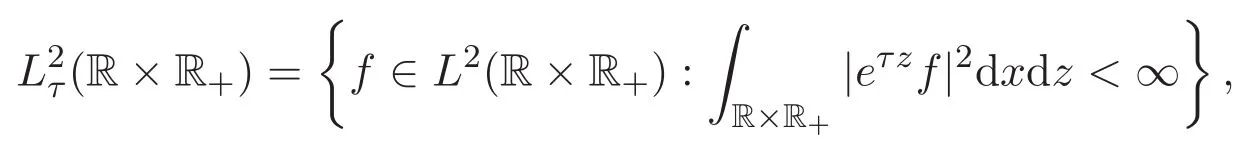
以及加权的Sobolev函数空间
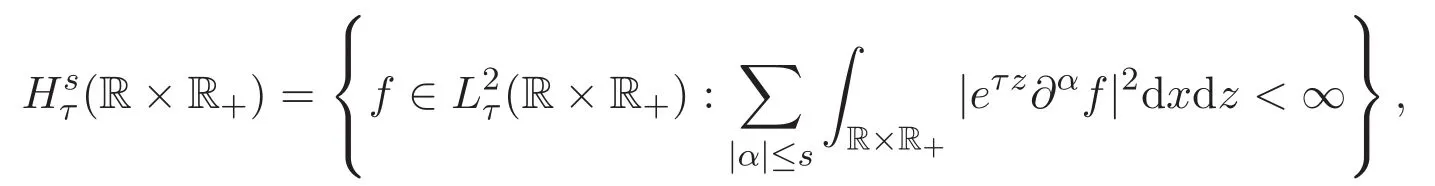
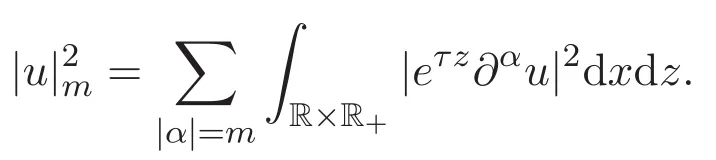
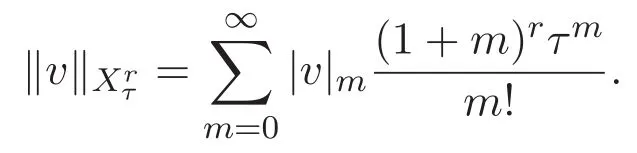
并记
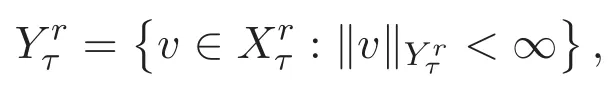
具有范数
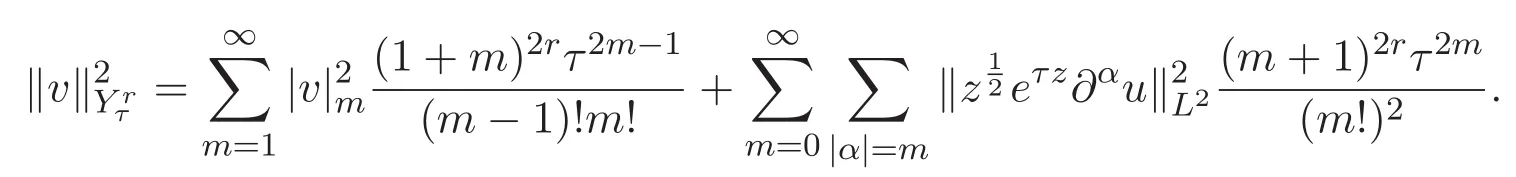
本文还需要利用到下列单变量实解析函数空间
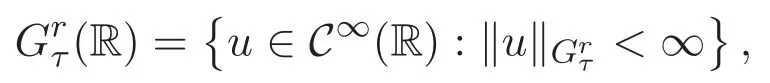
以及
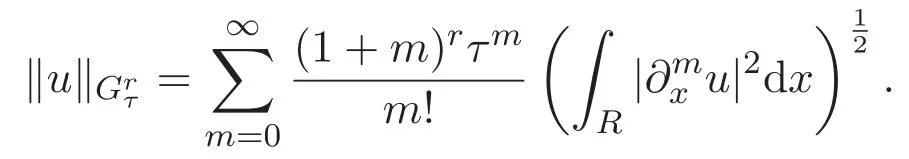
性质 2.1 设 0<τ′<τ,则有

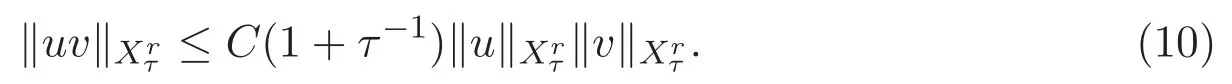
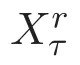
ACK 定理[14]设 {Bs:0 其中C不依赖于s,s′,t,u,v.此外F(0,t)∈Bs在(0,T)是连续的且存在固定常数K,使得‖F(0,t)‖s≤K.则对于 0 存在唯一解 u(t)∈Bs,0 对可测函数f,考虑下列方程 其中C>0不依赖于u,f. 利用分部积分有 从而 利用插值不等式有 由数学归纳法知对任意k≥0有 对上式关于 z 求偏导可化为 ∂t∂zf+up∂x∂zf+vp∂z∂zf=0,记 g=∂zf,则有 对应的边界条件 令 故得到了与方程组(8)同解的微分方程组 以及 为了验证边界层方程满足ACK定理的条件,需要证明下面两个引理. 证明 不妨设解析半径τ是关于t单调递减足够快的函数,从而有 考虑边界层方程组(8)的等价形式 对上式的方程两端作用微分算子Dα,并关于e2τzDαg做L2内积,可以得到 其中 从而 利用文献[16]的计算方法,而u由方程组(20)决定,利用命题3.3的结论及不可压性质,则有 求解常微分方程得 引理 3.2 设F如(18)式定义,在与引理3.1的假设下,则对于 上面估计的最后一步运用了解析函数的性质2.2,又根据命题2.3有 同理由于散度为零,从而 故有 其中 由条件知 结合(23)-(24)式可得 下面给出本文的主要结论. 证明 考虑边界层方程组(8)的等价形式 首先定义空间 则 另一方面,在上述条件下设(X1,X2)满足 则 因此对任意t>0,g(t,X1,X2)=g(t,X1,X2)|t=0=0,故有 满足边界条件 从而 结合(25)-(27)式可得 解常微分方程(28)可得 注:臧爱彬为孙小梅联合导师.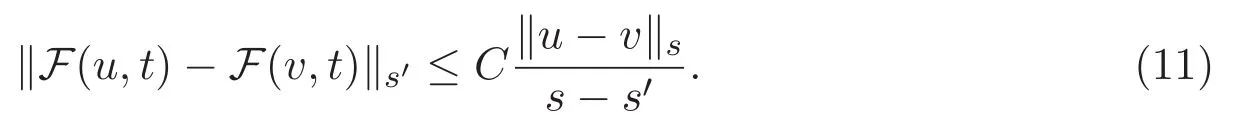
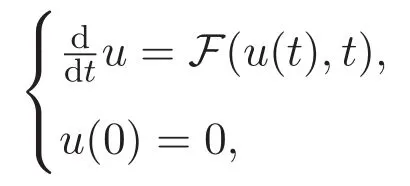
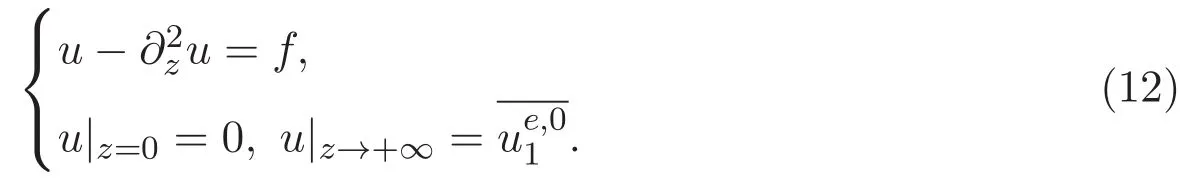

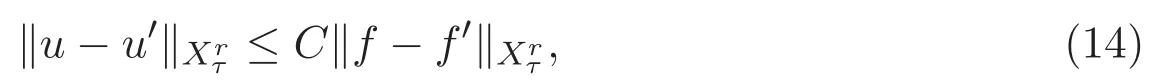
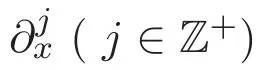
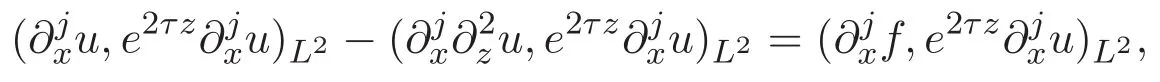
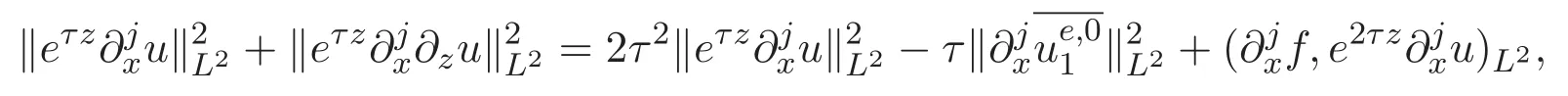
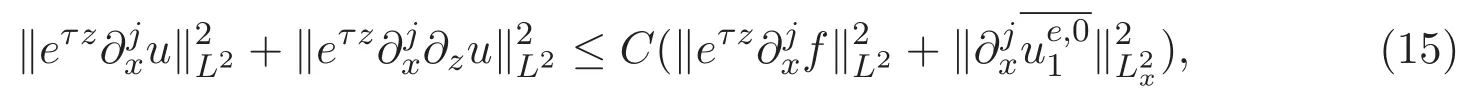
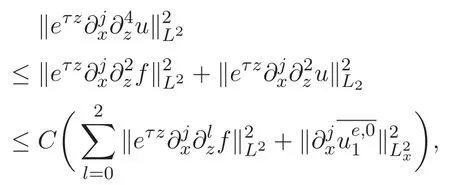
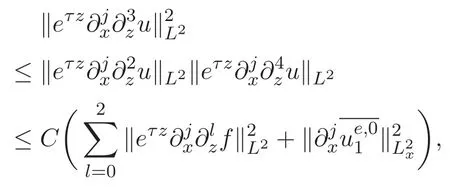
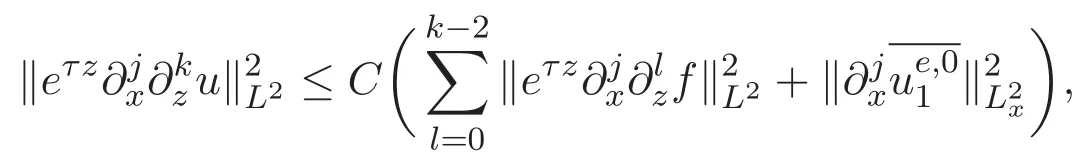
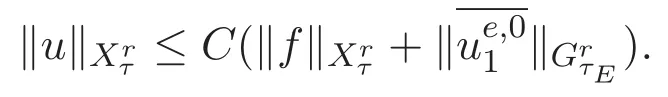
3 主要结论及证明