三维不可压缩非牛顿流体/Vlasov方程组的大时间行为

朱欢,方莉

(西北大学数学学院,陕西 西安 710127)

1 引言

本文研究三维周期空间中不可压缩非牛顿流体/Vlasov方程组的大时间行为,考虑如下方程组

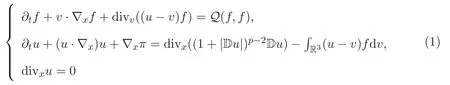
其初始条件为

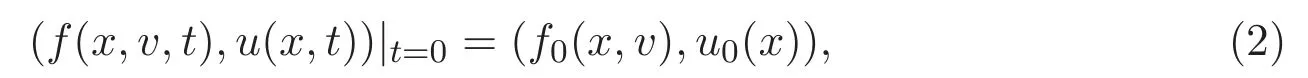
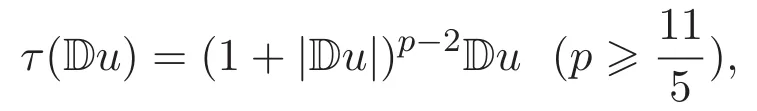
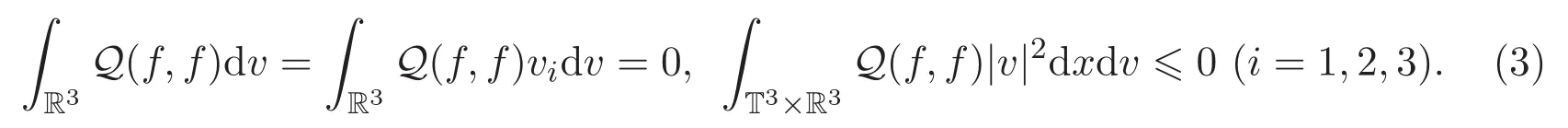
流体-粒子方程组是流体力学中一类重要的模型,常用来模拟流体与粒子的相互作用,由于它在生物学,药学,石化工业等领域的广泛应用[1-3],吸引了许多学者的关注.这里简单介绍流体-粒子耦合模型的相关结果.文献[4]首次给出不可压缩Vlasov-Navier-Stokes方程组弱解的全局存在性(N 6 2)和弱解的大时间行为(N=2,3),其中N空间维数.文献[5]讨论了周期区域中不可压缩Cucker-Smale-Navier-Stokes方程组弱解的全局存在性和时间衰减估计,之后,文献[6]证明了可压缩 Cucker-Smale-Navier-Stokes方程组强解的全局存在性,利用Lyapunov函数估计其大时间行为.在文献[6]的基础上,文献[7]介绍了一个新的Lyapunov函数,给出Vlasov-Navier-Stokes系统全局经典解的大时间行为,指出随着时间的推移粒子与流体速度呈指数衰减.关于流体-粒子方程组的其他结果见文献[8-9].

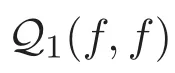
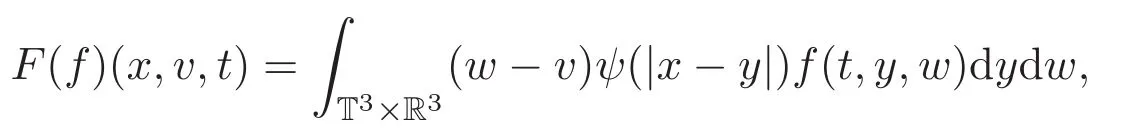
这里ψ(·)是非负,单调不减的光滑对称函数,研究了该模型三维周期区域中不可压缩粘性非牛顿流体与Cucker-Smale方程组弱解的存在性并分析了所得解的大时间行为.本文对初始能量提出小性假设,采用文献[11]中的Lyapunov函数,研究方程组(1)-(2)在三维周期区域下弱解的大时间行为.

首先,定义三维周期空间下的函数空间.

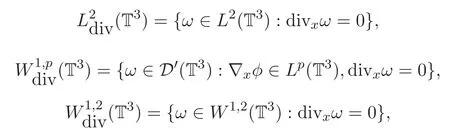
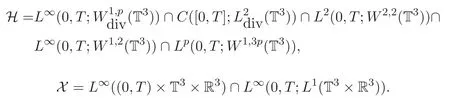
其次,给出方程组(1)-(2)弱解的定义和存在性理论.

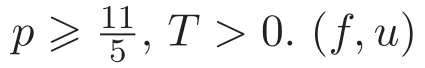
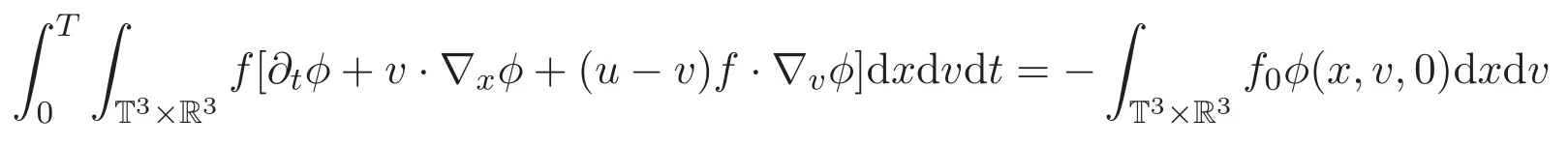
成立.

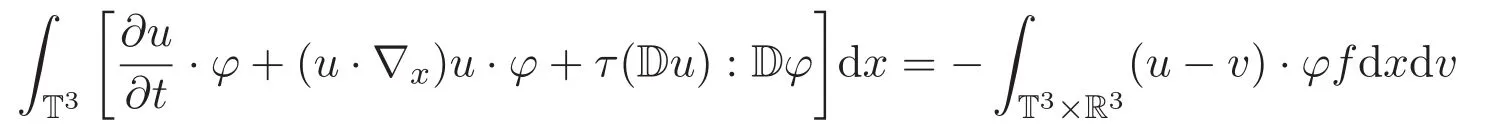
成立.

方程组(1)-(2)弱解的存在性,利用文献[11]的方法证明可得,本文主要讨论该弱解的大时间行为.

接着定义流体与粒子速度变化的平均量,具体如下:

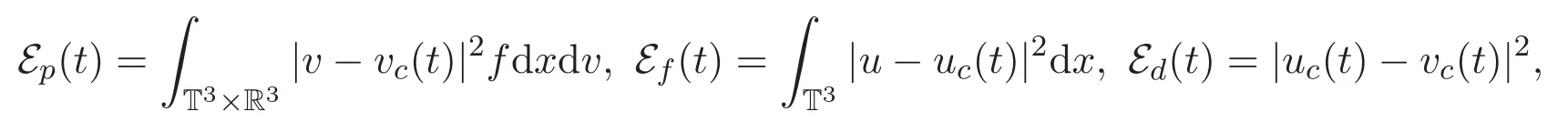
其中

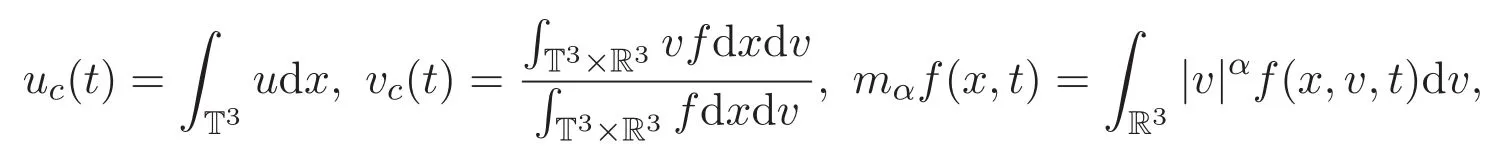
Lyapunov函数E为E(t)=2Ep(t)+2Ef(t)+Ed(t).

最后,阐述本文的主要定理.

定理 1.1 给定T>0.如果(f0,u0),m0f分别满足

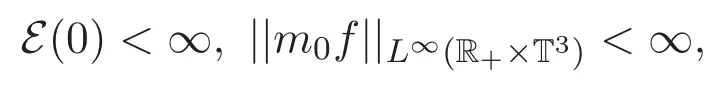
则方程组(1)-(2)弱解的指数估计E(t)6 E(0)e−γt(t∈[0,T))成立,其中

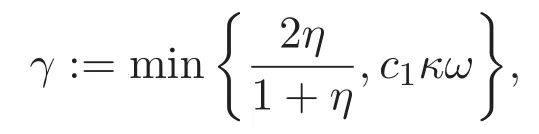
η是不依赖于时间t的正常数且

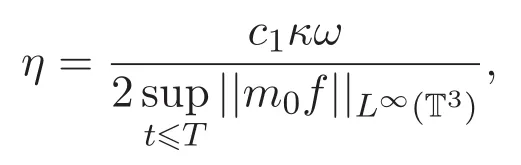
κ和ω分别是三维周期区域Korn′s不等式及Poincare′s不等式中的常数.

2 预备知识

下面给出证明定理1.1必需的两个引理.

引理 2.1 如果(f,u)是耦合方程组(1)-(2)的弱解满足

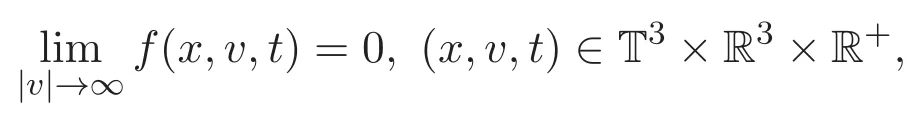
则

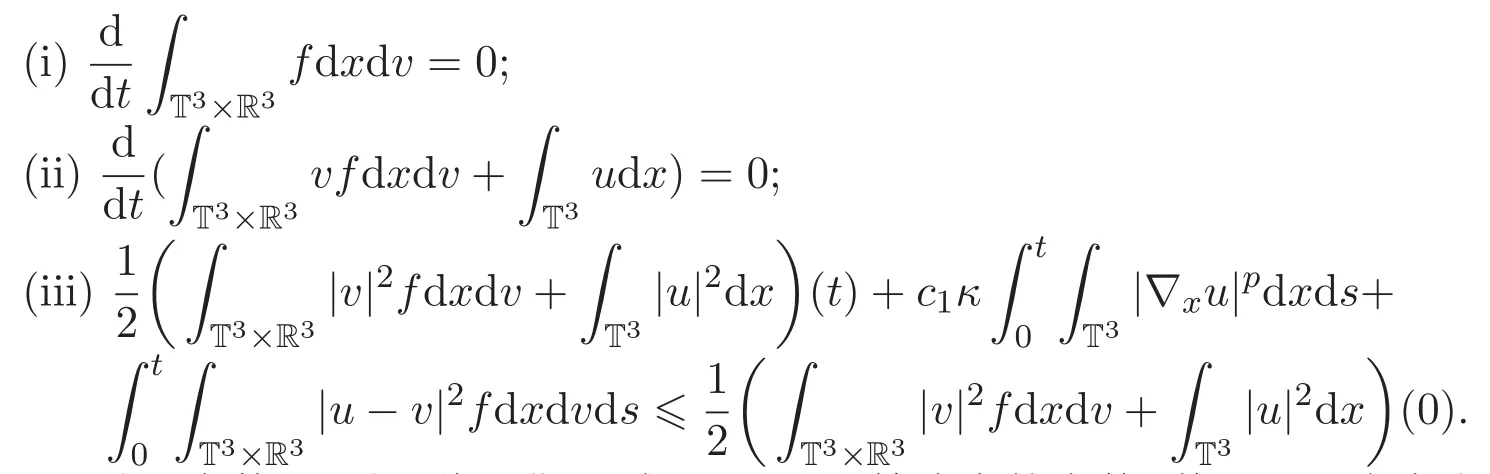
其中c1是正常数,κ是三维周期区域Korn′s不等式中的常数,其证明可参考文献[8].

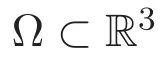
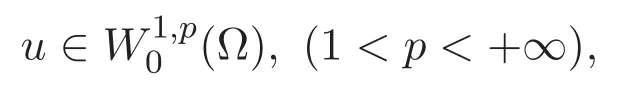
3 定理1.1的证明

为了符号的简便,记uc=uc(t),vc=vc(t).

引理 3.1 如果(f,u)是耦合方程组(1)-(2)的弱解,则

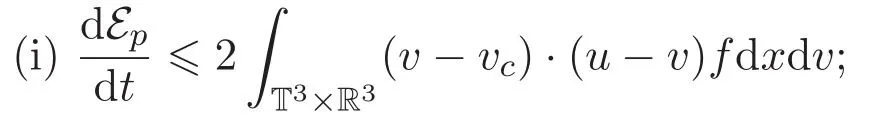
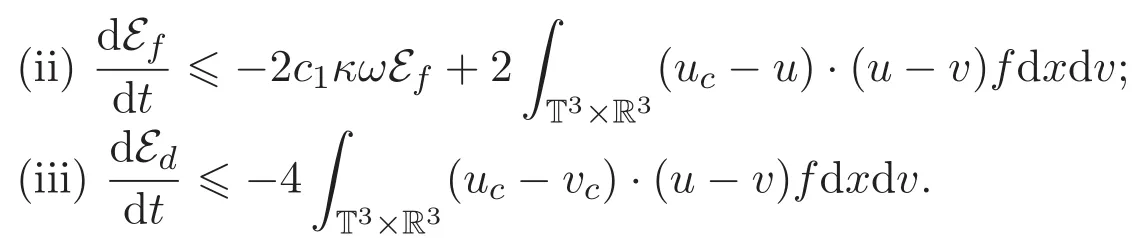
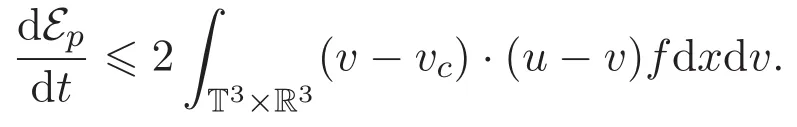
(ii)方程(1)2两端乘以测试函数(u−uc)且关于x积分可得

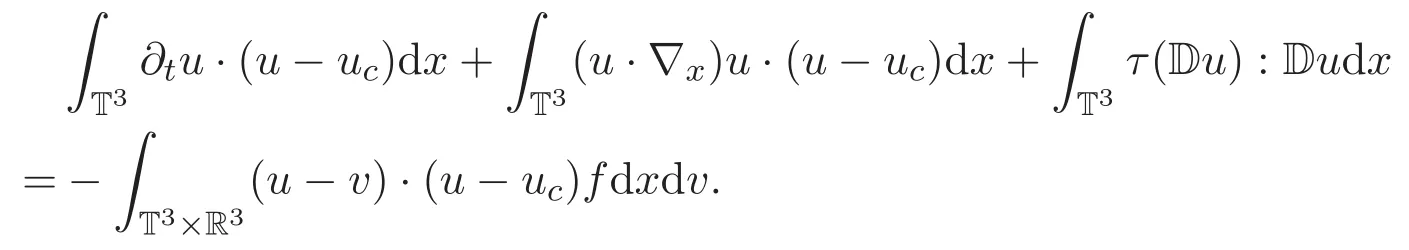
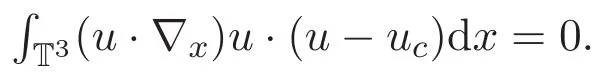
另一方面,利用 Korn′s和 Poincare′s不等式可得

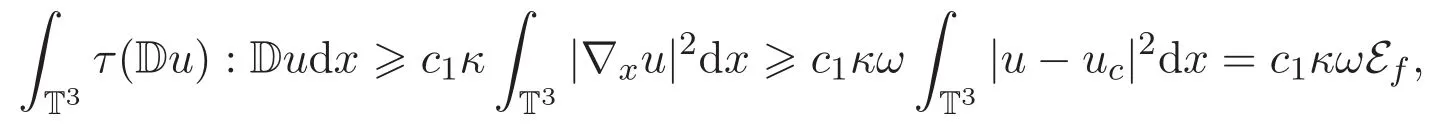
其中κ和ω分别是三维周期区域Korn′s不等式及Poincare′s不等式中的常数,c1为正常数.

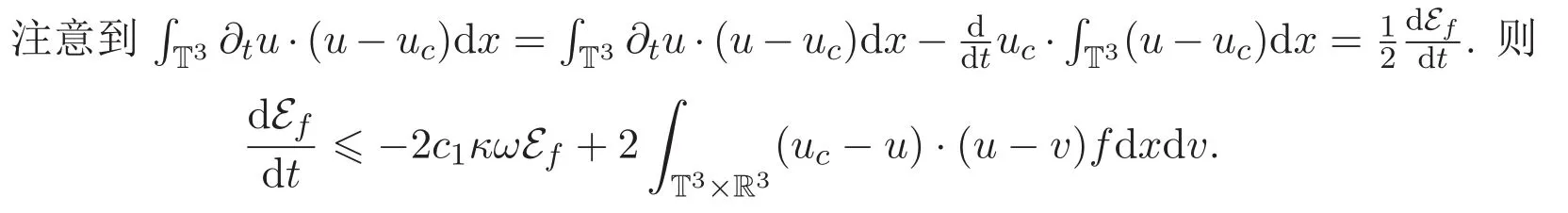
(iii)由引理2.1同理可证.

定理 1.1的证明 注意到E=2Ep+2Ef+Ed,结合引理3.1可得

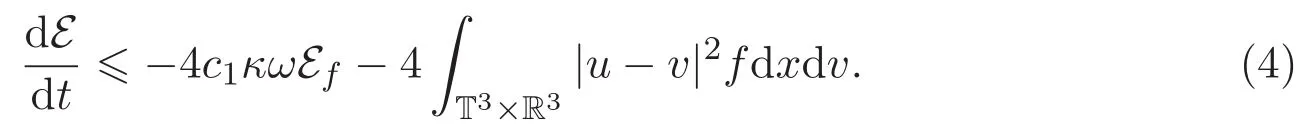
此外

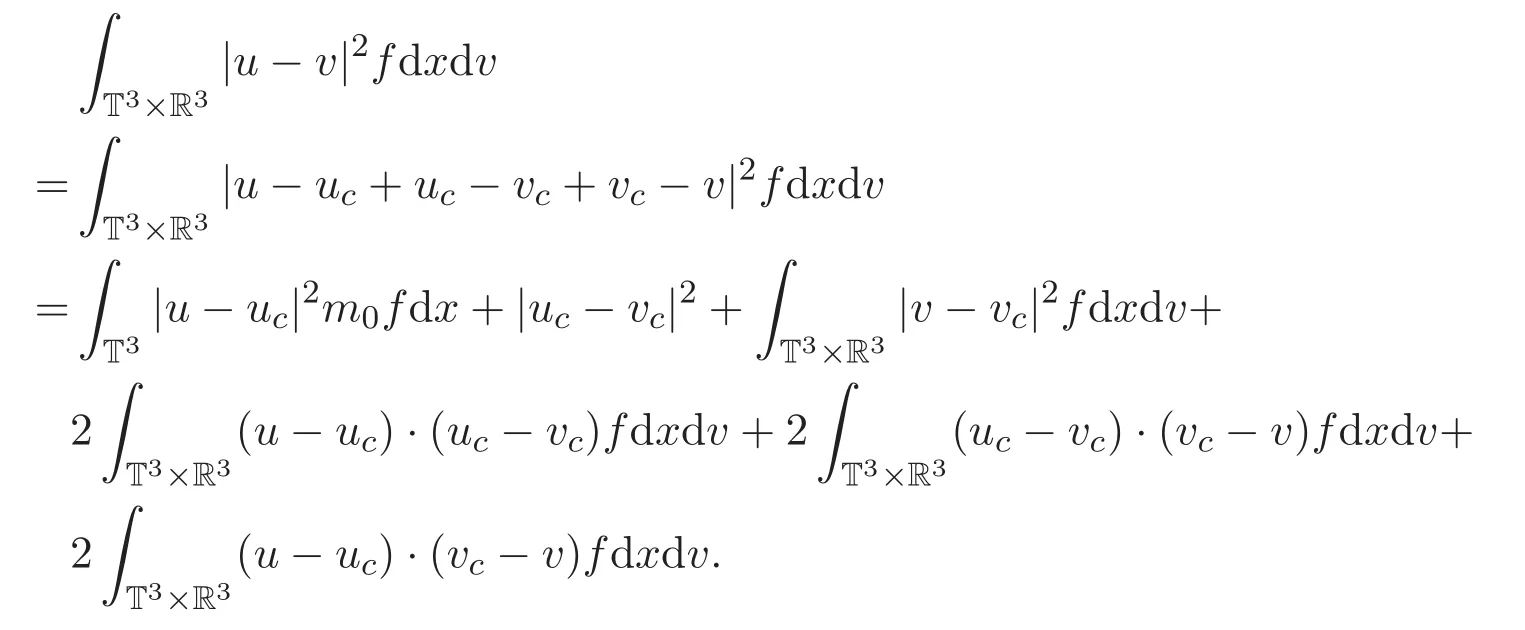
由vc的定义可知

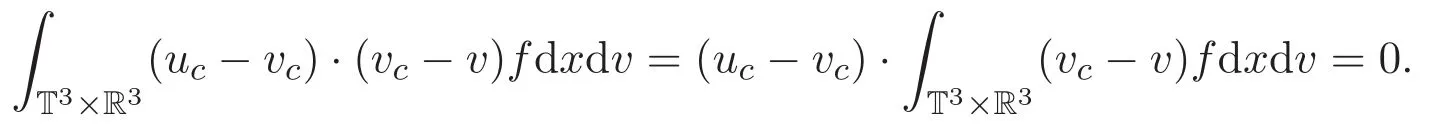
而且

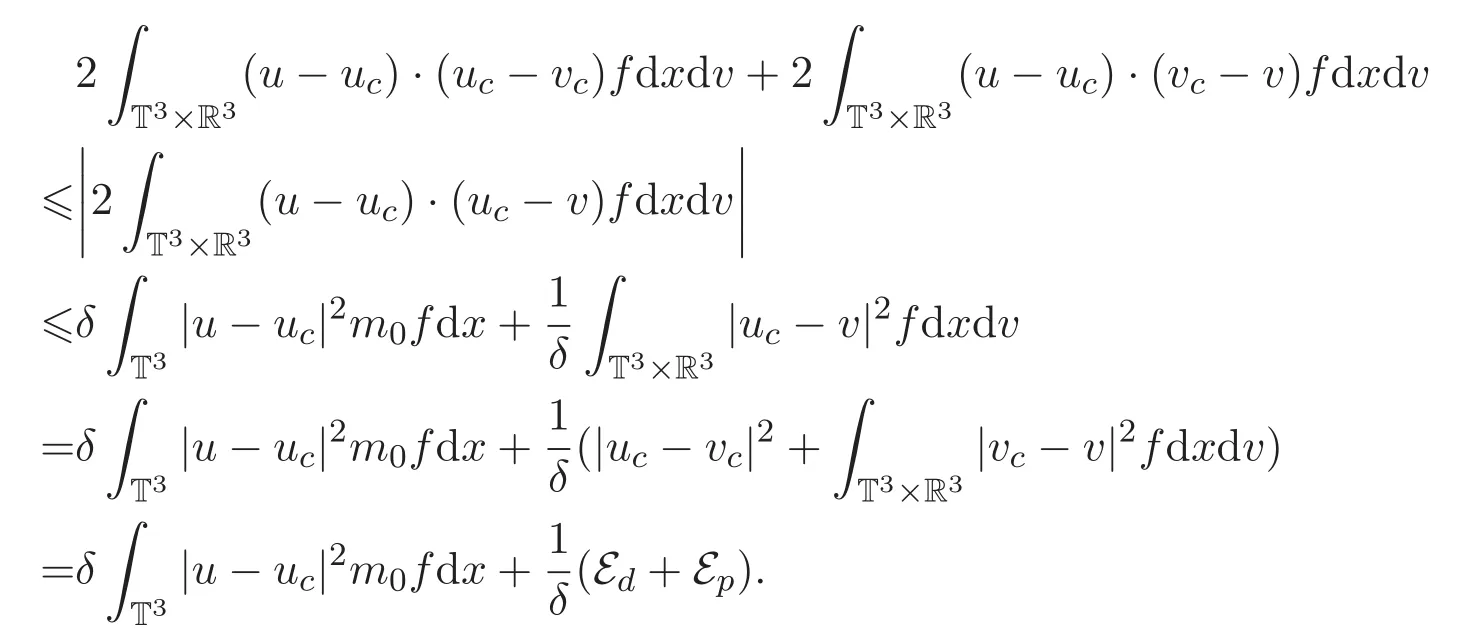
于是

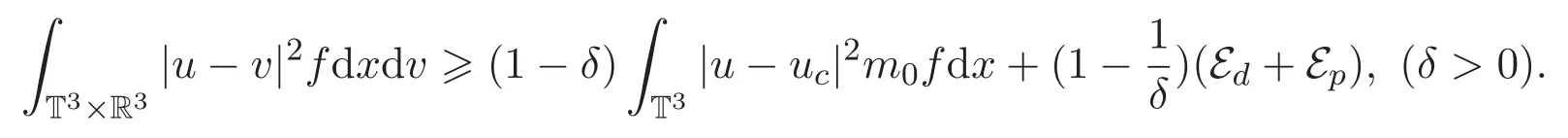
结合(4)式不难得到

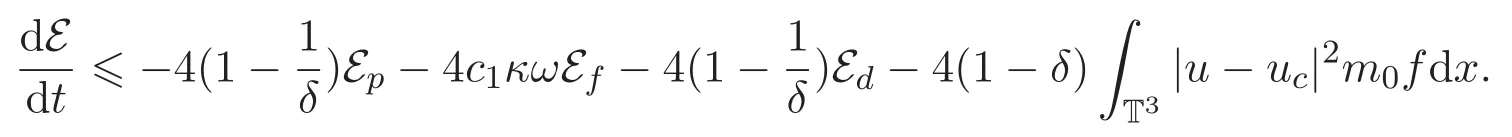
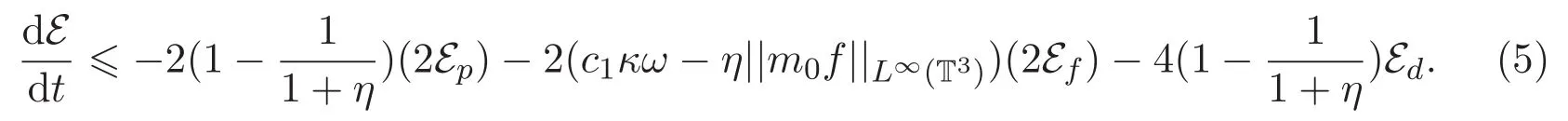
固定

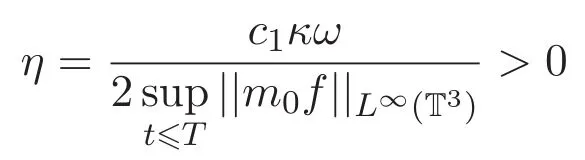
对 (5)式利用 Gronwall′s不等式可得 E(t)6 E(0)e−γt(t∈[0,T)),其中

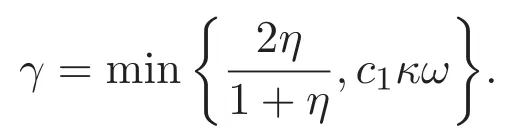
因此,定理1.1得证.