基于LSTM水稻生育期地下水水位预测——以黑龙江省查哈阳灌区为例

徐淑琴，乔厚清，王雅君，李仲裕，郭晓婷

（东北农业大学水利与土木工程学院，哈尔滨 150030）

农业稳健发展离不开水资源。在农业灌溉工程中，井灌、泉水灌溉、截潜流灌溉等地下水灌溉方式在农业生产中具有重要地位。我国北方地区由于气候原因，水资源短缺，地下水取水灌溉成为北方农业灌溉重要取水方式。以2019 年为例，全国供水总量6 021.2 亿m3，占当年水资源总量20.7%。其中，地下水源供水量934.2 亿m3，占供水总量15.5%；与2018 年相比，供水总量增加5.7 亿m3，其中，地下水源供水量减少42.2 亿m3。因此，合理规划与利用地下水资源对调控地下水水位，发展灌溉农业有重要意义[1]。

目前预测类算法主要有线性回归拟合、小波分析变换、时间序列分析等方法，而近年来神经网络与群智能算法成为有力研究工具，不仅为金融学与经济学等人文社会科学研究提供更高效和准确服务[2-3]，在自然科学层面也表现优秀。在水文水资源系列预测方面，神经网络与深度学习算法在降雨预测、气温预测、河川径流和给排水等方面表现优良，因此利用神经网络智能算法预测与分析水文序列并建立优质模型成为水资源分析领域重要发展方向[4-5]。近年来，各类统计模型研究趋于成熟[6]，包括人工蜂群算法[7]与RAGA 在内群智能算法、RBF 等传统神经网络改进算法在地下水埋深预测取得优秀成果[8-9]，改进的灰色系统预测模型在地下水资源时空分布与动态水位预测方面亦有深入研究[10-11]。近年来，学者改进BP 神经网络动态预测地下水水位与埋深[12-13]，将神经网络与小波分析结合建立模型预测灌区范围地下水位[14]。长短期记忆神经网络在其他地区地下水水位预测方面也取得一定成果，汪云等、闫佰忠等应用长短期记忆神经网络预测山东泰山地区地下水水位，通过分析参数发现长短期记忆神经网络在地下水水位预测中可取得较优成果[15-16]。因此，由以往地下水资源预测模型研究经验可知，包括LSTM 算法在内多类新型神经网络模型等智能算法预测模式，对掌握当前地下水资源量与未来地下水资源变化趋势，合理配置地下水资源，实现对地下水降落漏斗有效预警，以及促进农业水资源可持续发展及维护区域生态平衡发挥积极作用。

本研究在前人研究基础上，采用长短期记忆神经网络进一步研究地下水水位长期变化短期依赖问题。研究重点为建立合理稳定的预测模型，通过已有实测数据预测查哈阳灌区水稻生育期地下水水位，分析讨论其未来走势。建立可对地下水资源合理利用、灌区水资源优化配置方案的制订提供参考模型，有利于定量把握未来地下水资源变化规律。合理分析利用模型预测结果，合理制定地下水使用方案，以保障灌区农业灌溉需要，使地下水发挥其作用，也可在一定程度上制约地下水过度开采行为，预防地下水资源安全问题。

1 研究方法与原理

1.1 研究方法概述

Hochreiter 和Schmiclhuber 等深入研究传统循环神经网络（Recurrent Neural Networks，RNN）无法解决“长依赖”问题，并从基础上改进传统RNN，首次提出并全面论述长短期记忆神经网络（Long Short Term Memory networks，LSTM）[17]，Gers 等论述长短期记忆神经网络在遗忘规则基础上连续预测形式与过程[18]。目前，LSTM 神经网络发展较为成熟，在经济金融反向应用广泛，在水文序列分析应用少，从数据类型来看，各类水文序列与LSTM 结构契合。本文通过分析与利用LSTM 结构，建立以已有单变量数据为基础的预测模型，在误差分析方面，通过统计方法计算均值与均方根误差选择优质模型，通过幅度谱变换方法分析周期性以验证预测结果准确性。

1.2 LSTM原理结构

LSTM 是一种具有链式结构的RNN（见图1），与传统标准RNN 神经网络不同之处在于，传统RNN内部重复单元仅有一层tanh网络层，而LSTM内部重复单元有四层网络层，即三层Sigmoid 激活函数（见图2）与一层tanh激活函数（见图3）。

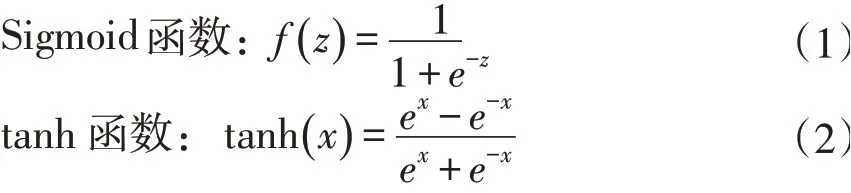
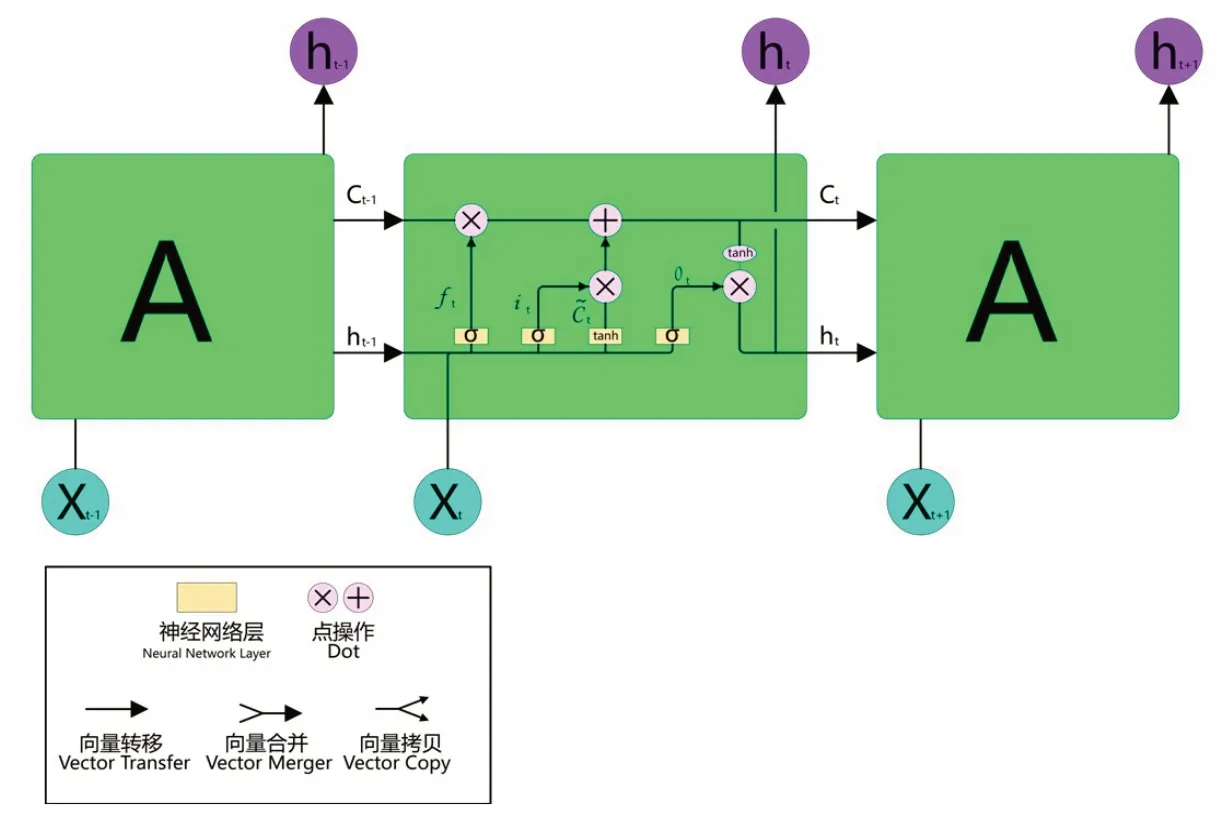
图1 LSTM神经网络结构Fig.1 Neural network structure of LSTM

图2 Sigmoid激活函数图像Fig.2 Image of Sigmoid activation function

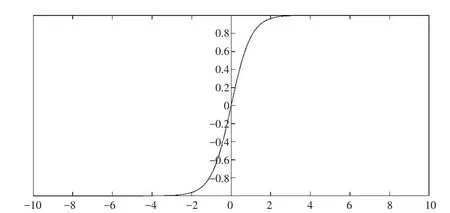
图3 tanh激活函数图像Fig.3 Image of tanh activation function

1.3 LSTM信息处理过程

在LSTM结构中（见图1），细胞状态（C）由“门”来控制。输入与更新门、遗忘门和输出门分别控制神经网络运作。

遗忘门选择性保留上一层神经元信息，以实现长短期记忆，遗忘门遗忘规则如下：

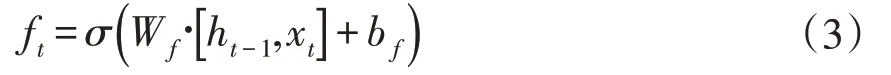
式中，ft为遗忘规则；σ为Sigmoid 激活函数，取值范围（0-1），0 为完全遗忘，1 为完全记忆；ht-1为上一细胞单元输出信息；xt为当前层输入信息；Wf为神经网络层权值；bf为神经网络层偏值。

输入与更新门对信息的操作为两步，首先，输入门决定需要更新的信息it，然后ht-1将和xt通过tanh层操作生成新细胞状态信息～Ct，输入与更新门规则如下：

式中，it为筛选后输入信息；为生成的待更新信息；Wi为输入门权值；bi为输入门偏值；WC为更新门权值；bC为更新门偏值；Ct为当前细胞状态信息；Ct-1为上一细胞单元状态信息。

输出门根据ht-1和xt判断细胞状态特征，分别通过Sigmoid 层和tanh 层得到判断条件与待输出向量，相乘得出该细胞单元输出ht，输出门规则如下：

式中，Ot为输出门判断条件；WO为输出门权值；bO为输出门偏值；ht为当前细胞单元输出。

每个当前细胞接收上一细胞状态、上一细胞输出和当前细胞输入信息，遗忘或更新操作信息，生成下一细胞可用状态信息与输出信息，以此构建连续可选择性更新信息链式神经网络，解决长短期依赖问题。

由此可知，LSTM是一种特殊RNN网络，主要用于解决长期依赖问题，地下水水位是时间序列水文数据，是一类长期依赖时序变化，既有明显年内变化，也有年际之间不均衡变化，适合使用LSTM预测地下水水位时间序列。

2 模型应用——以黑龙江省查哈阳灌区为例

2.1 灌区概况

查哈阳灌区位于黑龙江省齐齐哈尔市查哈阳乡，隶属于黑龙江农垦齐齐哈尔分局，是东北地区四大灌区之一。灌区水稻等作物产量大，品质优，承担东北地区乃至全国重要粮食生产任务，是重要的“人民米仓”。查哈阳灌区属第三积温带下线，年平均降水量470 mm，对灌溉农业依赖性极强，因此，灌区计划用水、水资源合理调度和地下水合理开发保护至关重要。

2.2 数据来源与处理

灌区地下水水位数据来源于查哈阳农场水务局，数据来源包含一跌水站、七联站、联合站、十字桥站、东风站、兴隆站、新立站和五跌水站共8个观测站实测数据，其中前6个站各有两口观测井，新立与五跌水站各有一口观测井，由于一跌水站、新立站、五跌水站与兴隆站2#观测井多年数据缺失严重，因此不予采用（见表1）。

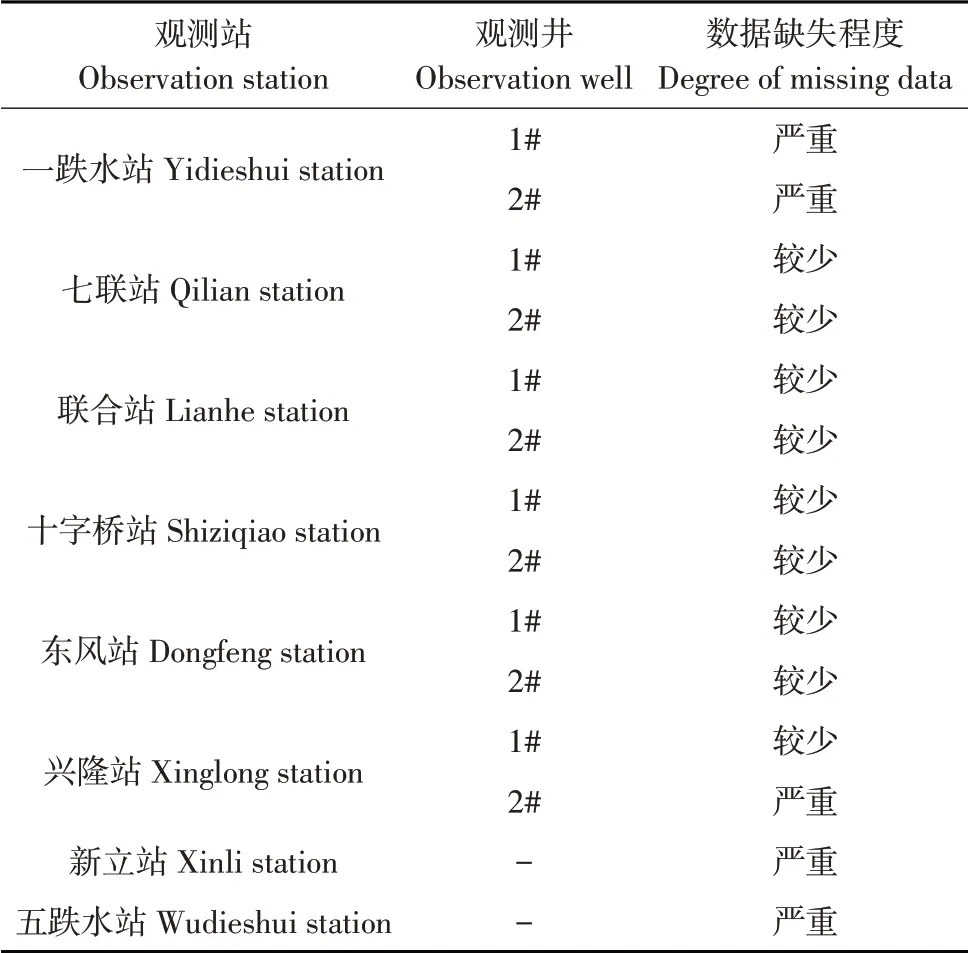
表1 各测井数据缺失程度Table 1 Degree of missing data of every obsveration station

数据实测时间跨度为2001～2018 年共18 年，由于地下水水位预测结果主要用于农业灌溉，且黑龙江地区冬季漫长，气温较低，地下水处于冰冻期，冬季数据不予采用，仅采用每年4～8月水稻生育期用水高峰数据。

训练筛选模型采用9个观测井实测数据，缺失的少量数据利用线性回归及取均值等方式补全，每个独立观测井有2001～2018 年共90 个月地下水水位数据，9 个观测井共有数据810 个。测井年内取5 个月水位数据，由9 个测井数据折线图可看出，灌区地下水水位年际变化有较明显周期性。年内变化趋势一致，4 月与8 月地下水水位较高，用水量较少，5～7月地下水水位较低，由于水稻处于拔节育穗期，作物缺水敏感指数较高，农业灌溉用水量增多。

实测数据具有较明显年际与年内规律，使用模型LSTM预测该区地下水水位长期变化，训练与预测操作以单个观测井90 个数据为基础，训练集占比90%，预测集占比10%，即每次训练训练集81个数据，测试集9个数据（见表2，图4）。

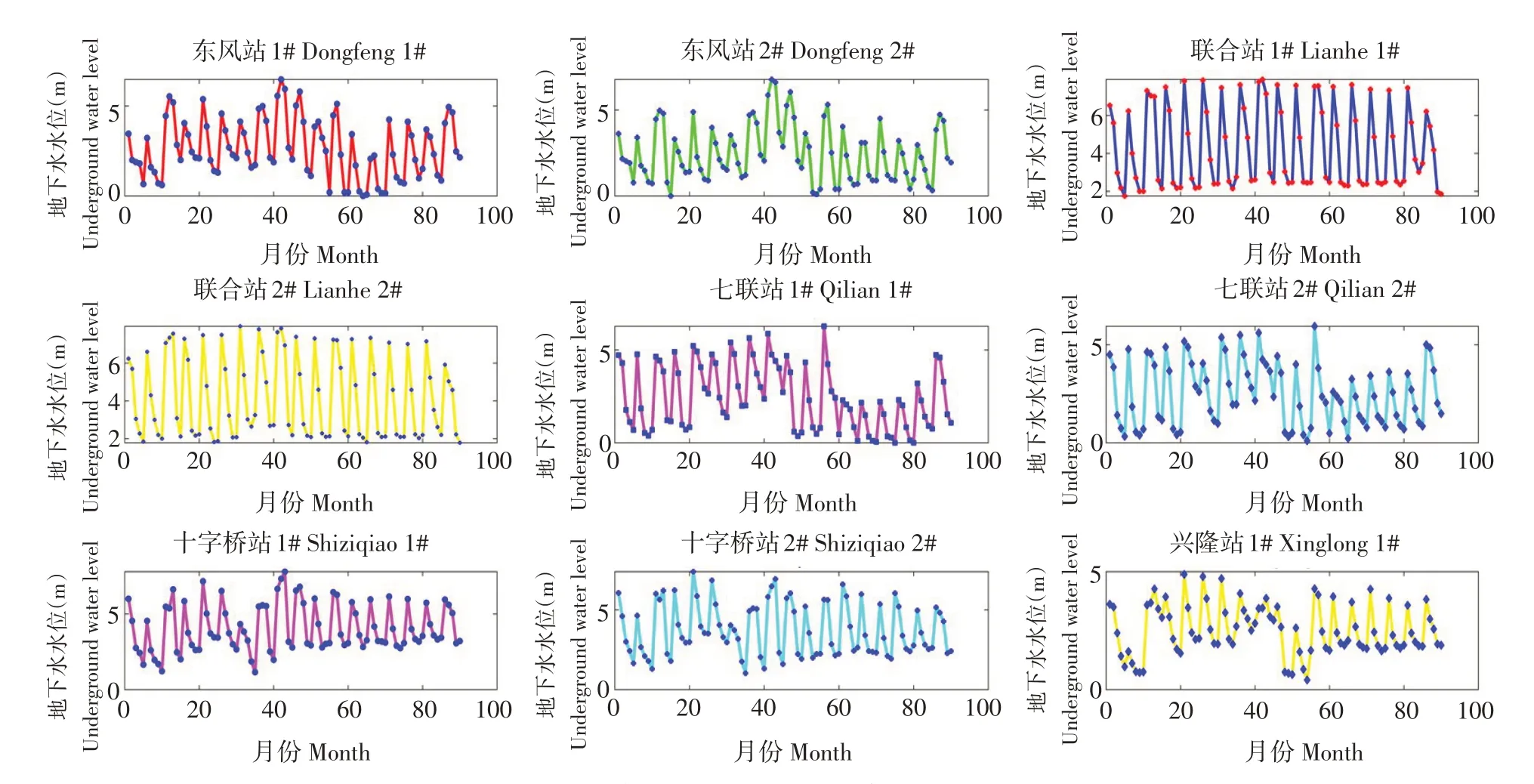
图4 各观测站2001～2018年实测水位Fig.4 Measured water level of each station from 2001 to 2018

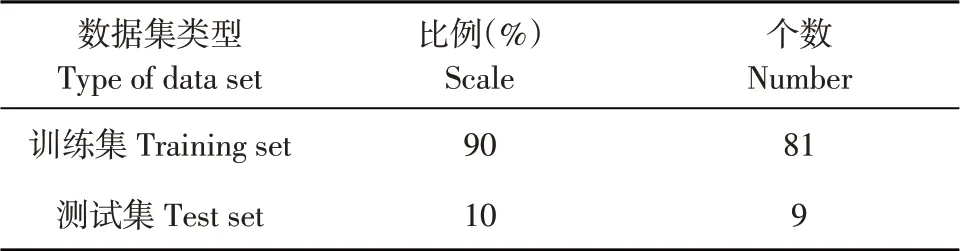
表2 数据集划分Table 2 Data set partition

2.3 模型训练

训练过程中，模型训练及测试9 个测井数据集，测试集占比低，多次训练每个测井数据集，每个测井数据集选取1个最优的训练结果作为该测井代表NET。

训练时，以前N-1 个数据为交替时间部预测第N 个数据，模型隐含层单元为96×3，训练限制步数为250 步，梯度阈值设置为1，初始学习率为0.01，在125步时乘以0.2，降低学习率，防止模型进入过学习状态。其中一个测试集训练过程如图5所示，在训练步数达到约150步开始收敛，其他测试集训练过程类似。

2.4 误差分析

对9 个测井训练得出模型分析训练误差（见表3），在9个观测站训练结果中，兴隆1#、七联2#两个测井训练结果均方根误差（RMSE）较小。

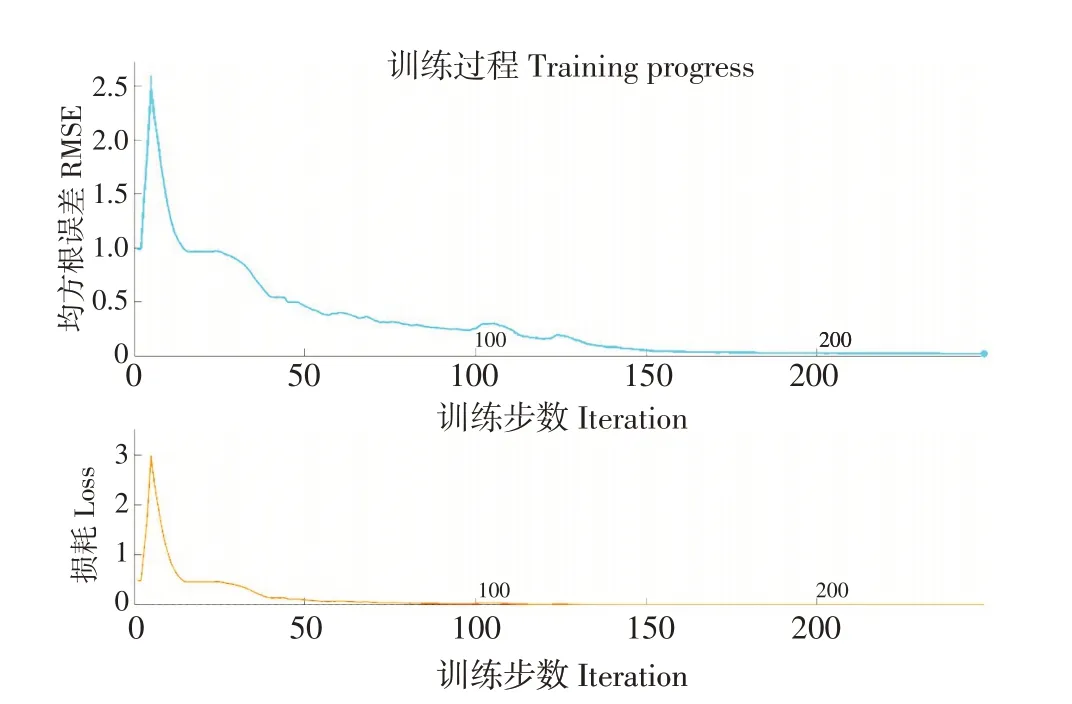
图5 训练过程Fig.5 Training progress

训练测试结果如图6所示，七联2#值与实际值平均误差为-0.2176，以统计显著性水平“α=0.05”，选用独立样本t检验方法检验结果，得出H=0，P=0.3087，置信区间CI=[-0.6865,0.2512]。兴隆1#预测值与实际值平均误差为-0.0714，以统计显著性水平“α=0.05”，选用独立样本t检验方法检验结果，得出H=0，P=0.4415，置信区间CI=[-0.2782,0.1355]。由统计分析结果可知，七联2#与兴隆1#对应预测模型表现优秀，可用于预测查哈阳灌区地下水位。

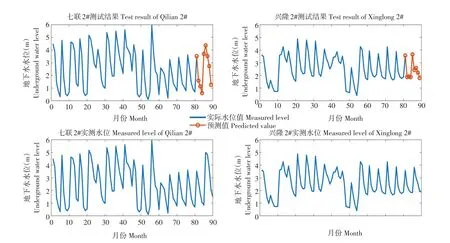
图6 七联2#、兴隆1#测试结果Fig.6 Test results of Qilian 2#and Xinglong 1#

3 模型预测

3.1 预测前处理

利用表3中均方根误差表现较优的七联2#、兴隆1#训练生成的LSTM 模型主体预测该区2019～2036年共18年地下水水位。

初始化处理数据，处理过程如下：

式中，Xj为标准化输入数据集；Xi为初始数据集；为初始数据集均值；σD为初始数据集标准差。预测结束后需按上式逆方向还原数据。

3.2 预测结果与分析

将七联2#、兴隆1#2001～2018 年数据分别带入各自LSTM 模型中预测，预测长度为90。预测过程中，由于使用GPU 加速需设置并行环境并集成CUDA 3.0 以上的GPU，而GPU 加速计算原理为碎片化任务并充分利用GPU 物理结构，在数据量较大情况下可提高程序运行效率。CPU与GPU运行模式仅在数据量不同情况下运行效率有差异，不影响模型计算结果。实验机器不满足GPU运行条件，且数据量较少，因此Execution Environment 设置为CPU运行模式，即不采用GPU加速，结果如图7和8所示。

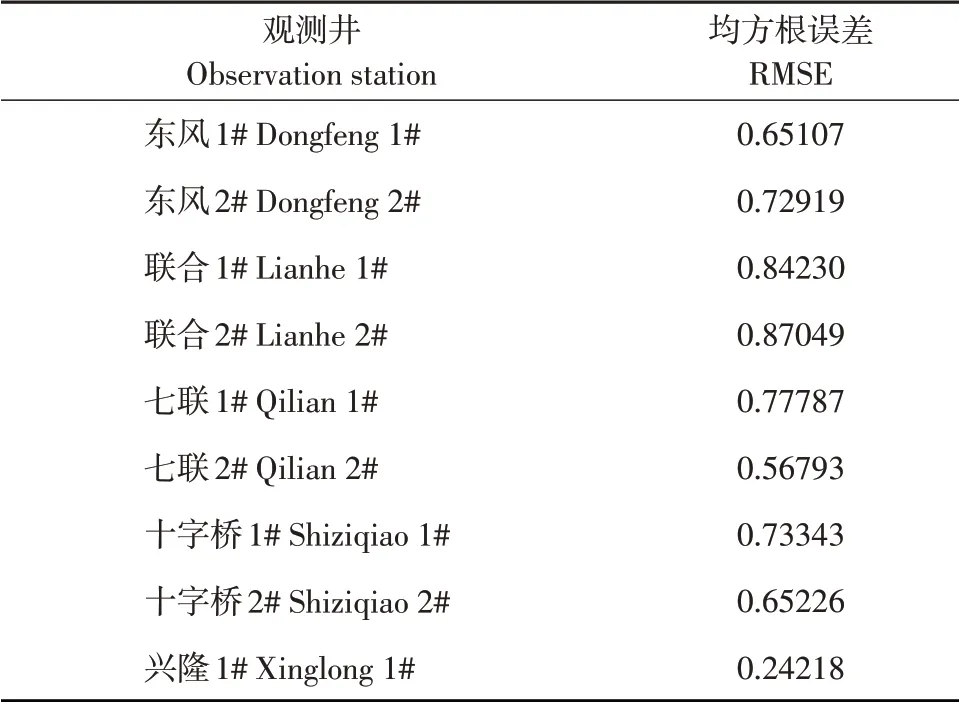
表3 各测井数据集训练误差Table 3 Training error of each logging data set

分别计算七联2#、兴隆1#两个模型实测及预测结果均值与标准差，由表4可知，模型预测水位结果，均值和标准差均与实测资料接近，模型预测2019～2036 年水位结果与2001～2018 年地下水水位实测成果数值范围相符。用快速傅里叶变换分别对比两测井实测与预测结果，分析二者频域频率，采样频率为1 000 Hz。由图9 两测井幅度谱实测值与预测值幅度谱对比图可知，4个幅度谱图主要频率均为400和200 Hz，即实测水位周期与预测水位周期均为5 个月、2.5 个月，且单测井实测与预测幅度谱走势分布接近，模型预测2019～2036年水位结果与2001～2018年水位变化趋势与周期性接近。因此，模型运作良好，可用于查哈阳灌区中长期地下水水位预测。

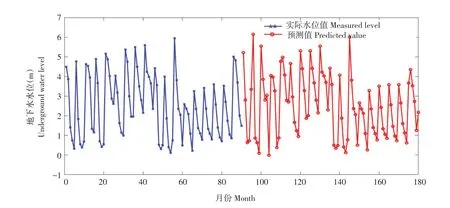
图7 七联2#实测水位与预测水位结果Fig.7 Measured water level and predicted water level results of Qilian 2#

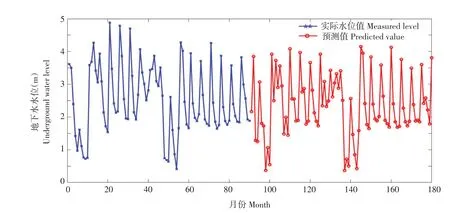
图8 兴隆1#实测水位与预测水位结果Fig.8 Measured water level and predicted water level results of Xinglong 1#

表4 模型预测结果均值与标准差Table 4 Model prediction results mean and standard deviation

图9 实测、预测水位幅度谱对比图Fig.9 Comparison chart of measured and predicted water level amplitude spectrum

4 结 论

a.长短期神经网络由于“门”结构优秀逻辑，可较好预测长依赖问题。查哈阳灌区水稻生育期地下水水位具有较明显周期性变化规律，训练LSTM模型时，选用适当测井对应数据集可取得较优质训练结果。

b. 两个测井模型预测结果幅度谱分析结果显示，该区地下水水位具有较为明显周期性，实测资料与预测结果均以5 月与2.5 月为变化周期，长期预测结果与实测资料对比可知，二者均值与标准差差值极小，因此模型可用于测定查哈阳灌区地下水水位。

c.LSTM 预测模型可改进传统链式神经网络无法反应长短期信息的缺点，有效筛选与传达信息，一定程度上增加预测精度。但由于地下水水位变化因素复杂性，气候、径流、降水以及人类生产活动等对地下水位变化均有一定影响，时间序列数据预测具有一定局限性。因此，本模型仅用于中长时段周期性预测，无法满足短期精准预测要求。