2种影响相位干涉仪测向的问题分析

郭 辉，吉荣华，张 君，吉 宇，翟宏骏，柯 金

（中国航天科工集团8511研究所，江苏南京 210007）

0 引言

相位干涉仪具有测向精度高、侦测频段宽、设备量小等优点，现已成为无源系统测向设备的重要手段之一[1-2]。在工程实践中，微波接收通道由于尺寸、器件布局等条件限制，可能无法保证不同通道间连接电缆等长，不等长会引入通道间相位差的误差，此种误差能否通过通道误差校正技术进行修正是本文关注的重点问题之一。另外，微波通道接收信号时，存在通道间同频信号的相互干扰，这种干扰对通道间相位差的影响程度有多大、工程中能否忽略这种相互干扰也是本文研究的重点问题。

1 相位差模型

相位干涉仪相位差模型示意如图1所示。

测向需求的相位差为2天线间距D引起的相位差，即：

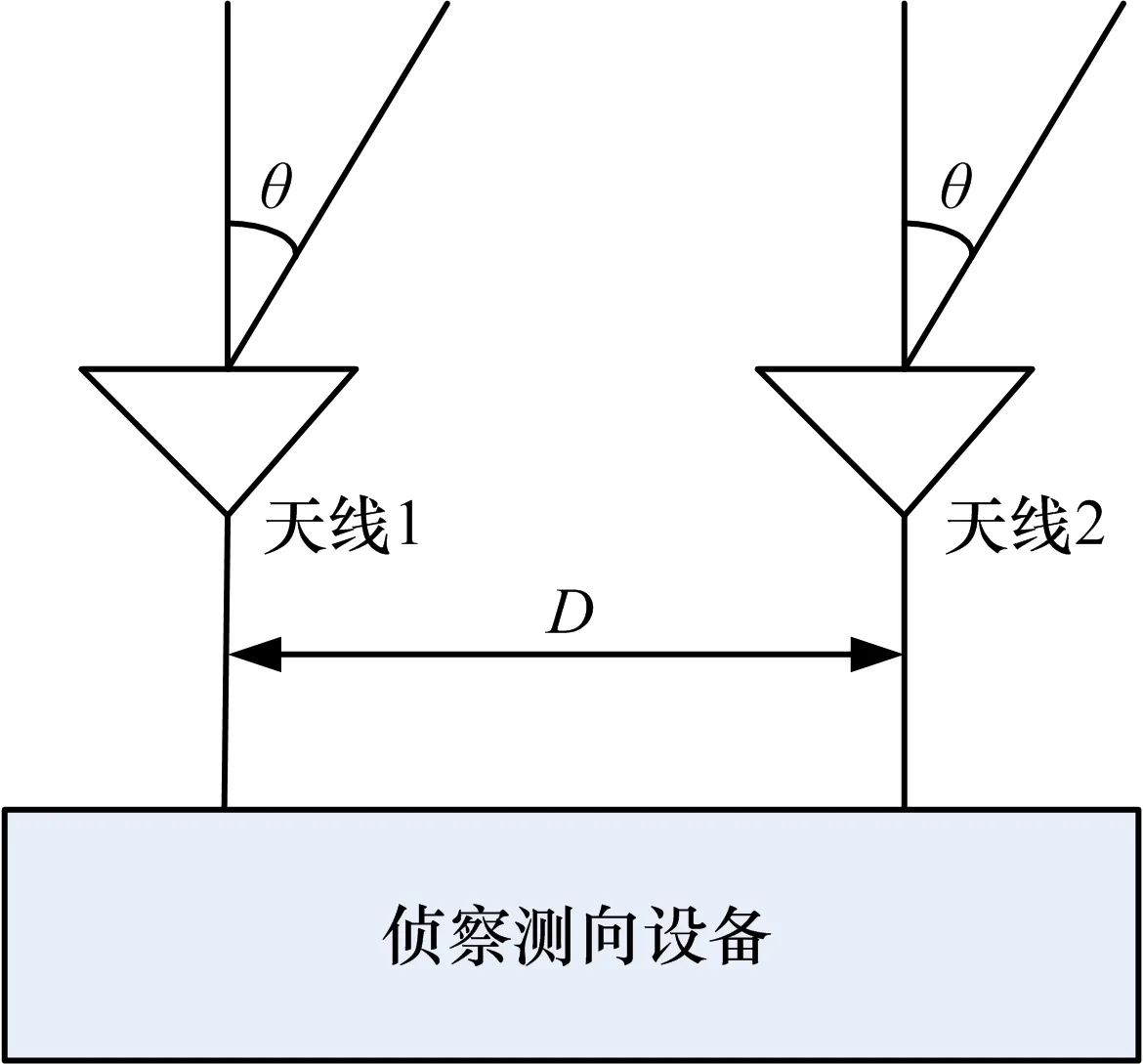
图1 相位干涉仪相位差模型

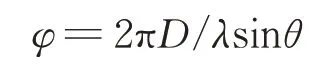
数字鉴相给出的相位差包括间距D引起的相位差以及通道不一致性引起的相位差，其中通道不一致性引起的相位差由多种因素导致，比如天线相位失配、天线后电缆不等长、通道器件性能以及噪声不同等等[3]。

2 不等长影响

2.1 不等长分析

假设鉴相总的相位差表示为：

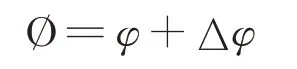
式中，φ为间距D引起的相位差，∆φ为通道不一致性引起的相位差。校正相位差的目的是消除∆φ的均值量。

目前校正相位差的方法没有考虑天线相位失配导致的误差，一般认为这个误差与天线布阵要求的容差相比较小，对测向性能影响不大；从天线到微波前端，再到数字AD中间会经过较多电缆进行连接，通道电缆长度无法保证严格等长，将引入一个固定相位差，理论上可以通过校正完全消除，实际中电缆不等长的长度需要受到校正频率步进的限制，必须满足校正频率步进内此相位差的波动量与天线布阵要求的容差相比较小；通道器件性能以及噪声不同等引起的相位差是一个随机变化量，校正处理只能消除均值影响，因此其引起的相位差波动量将直接影响测向的性能，一般对其在校正频率步进范围内的相位差稳定度要求较高，需满足天线布阵容差要求。当然还有一些其他因素对干涉仪测向性能有一定的影响，比如天线安装误差、极化、“圆锥效应”角误差等，目前传统的校正方法并没考虑这方面的因素，在高精度测向应用的场合需要进一步进行校正处理，这里不进行分析。

根据上述分析，通道不一致性引起的相位差∆φ包含一个固定分量和随机分量，表示为：

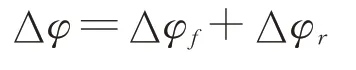
式中，∆φf为固定分量，∆φr为随机分量。

鉴相总的相位差可重写为：

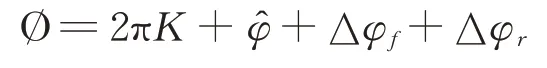
式中，M为固定分量的模糊数为±180°内的反转后相位差，实际校正过程中，校正消除的为从公式上看还保留了一个2πM，这个量是否对测向结果产生影响是一个需要分析的问题。

分析这个问题，需要分析具体的解模糊过程，从上面的公式看，跳模校正不会影响到测量相位差，而解模糊的建模是基于间距D引起的相位差而进行的，即平常见到的干涉仪解模糊推导公式都是2πK++∆φr的建模，只要相同，跳模与不跳模校正并不影响解模糊过程[4]，例如3天线2基线解模糊过程，建模解模糊公式：

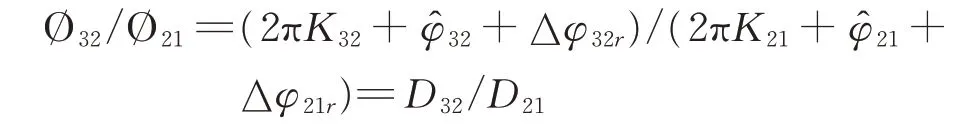
从公式看，解模糊过程仅考虑间距不同引起的相位差，与固定分量跳模无关，只要校正消除固定分量即可。

2.2 不等长仿真验证

理论上，不等长引起的相位差为固定分量，可以通过校正完全消除，但实际校正过程中，频率步进不可能过细，这就要求不等长的长度不能任意长。经过简单推导可有相位差变化量、不等长长度L和频率变化量的关系为：

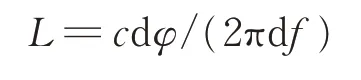
假设校正步进为10 MHz，相位差误差要求不超过10°，长度限制为：

因此，实际中要根据布线容差要求，对不等长长度L提出相应的要求。

下面给出一个3基线系统解模糊的仿真，无跳模（M32=0，M21=0）和跳模（M32=4，M21=1）情况下，解模糊概率和测向误差分别如图2和图3所示。

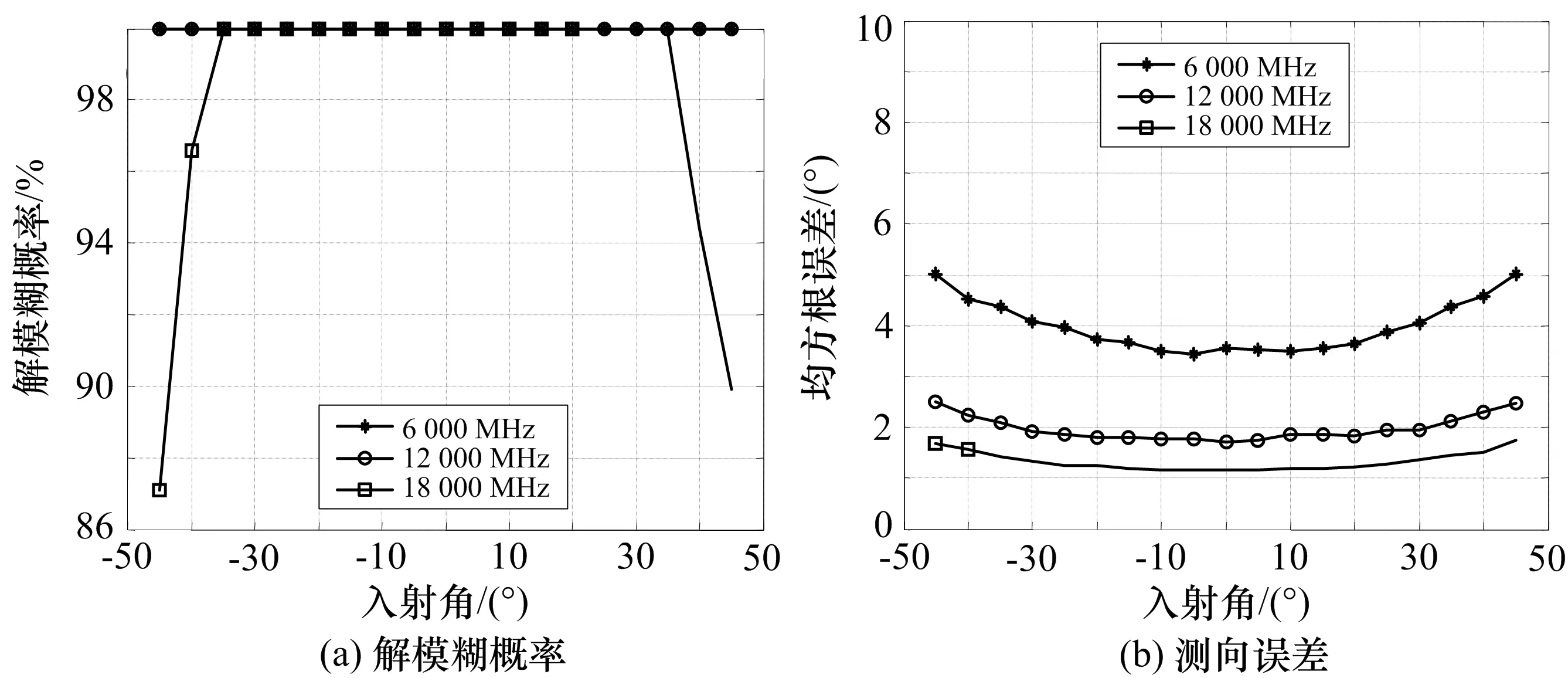
图2 无跳模情况下解模糊概率和测向误差（M32=0，M21=0）

图3 跳模情况下解模糊概率和测向误差（M32=4，M21=1）

可以看出，两者基本无变化，说明跳模引起的固定误差不影响测向解模糊，经过校正处理可消除不等长带来的影响。

3 隔离度影响

3.1 隔离度分析

假设通道2接收到的信号为：

则通道1接收到的信号为：

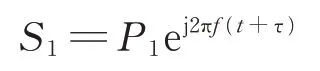
式中，τ=Dsinθ/c，P1、P2分别为各通道接收到信号的幅度。当通道之间相互干扰时，各通道接收到的信号可表示为：

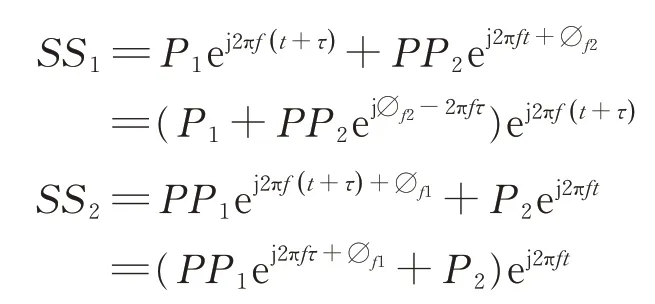
经过鉴相后，合成前后2相位差之间的变化为：

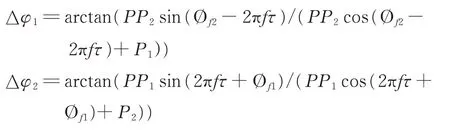
因为P1≈P2≫PP1≈PP2，上式中分母第一项可以忽略，此时当Øf2-2πfτ=180k+90°，2πfτ+Øf1=180k+90°，k=0,±1,±2,…时，相位差之间的变化取最大值：

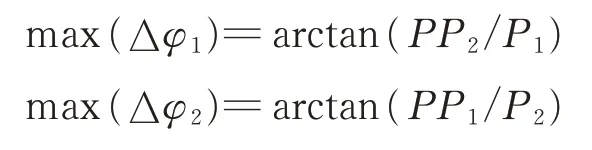
因此2路之间相位差变化最大值为：

为了剔除背瓣入射信号，设计中一般在测向天线阵背后增加一路通道用于比幅测向剔除背瓣信号，但当信号从背瓣入射时，若通道隔离度不够，背瓣通道会对测向通道形成干扰，假设从背瓣入射的信号为：

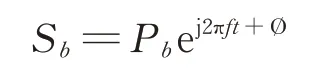
式中，Ø 为背瓣侦收信号的初相位。此种情况下，由于测向通道从背瓣侦收到信号，幅度一般比较小，这时不再考虑测向通道之间的干扰，各通道接收到的信号可表示为：

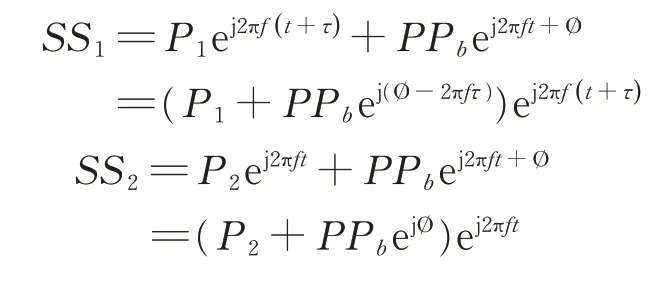
经过鉴相后，合成前后2相位差之间的变化为：

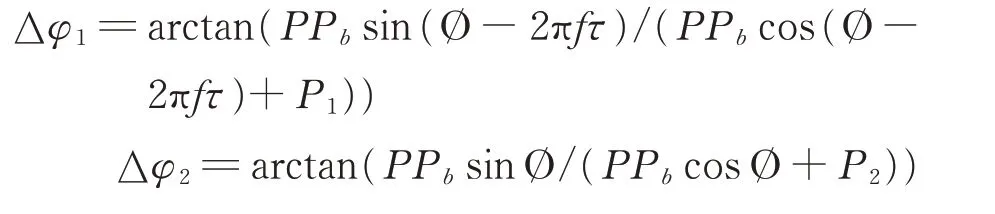
当PPb≈P1=P2时：

此时，相位差变化为：

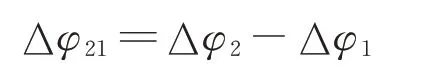
3.2 隔离度仿真验证

根据上述推导可知：

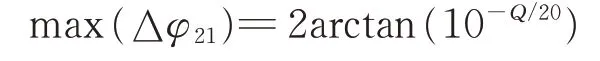
式中，Q为隔离度（dB），进一步假设2路之间隔离度为30 dB,2πfτ=90°，根据上述推导可知：

不考虑噪声情况下，1 000次蒙特卡罗试验结果如图4所示，可以看出与理论分析结果相同，同理，可以获得不同隔离度对应的相位差测量误差。

4 结束语

本文从解模糊过程证实了天线不等长引入的相位差跳模对解模糊测向无影响，推导了一定校正步进条件下，相位差误差与不等长之间的关系，可供微波前端通道设计参考。通过数据建模分析了通道间同频干扰带来的相位差测量影响，推导了通道隔离度对相位差测量影响的理论公式。本文成果对从事相位干涉仪测向的人员具有较好的参考价值。

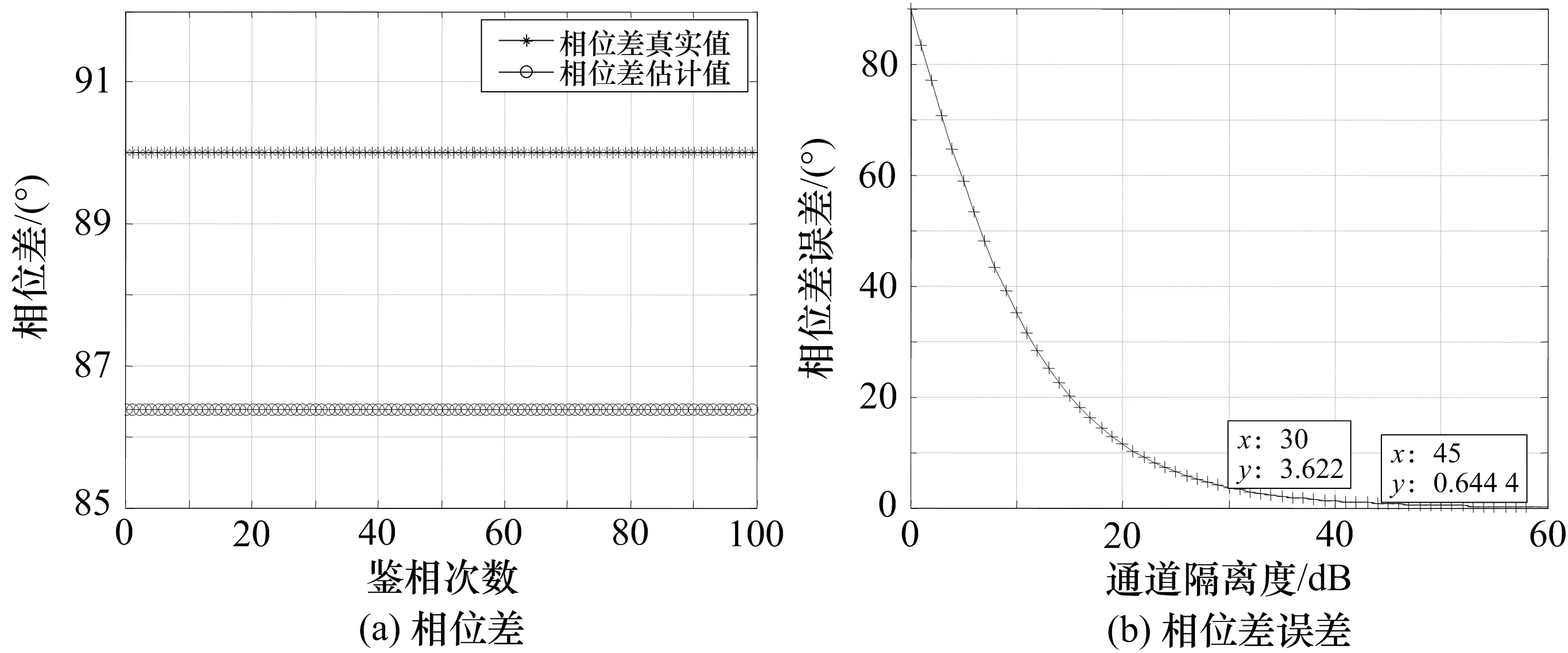
图4 通道隔离度对相位差测量的影响