雷达信号时差频差测量定位工程实现技术研究
王克让,洪春冲,徐学华,柯 金,卢 鑫,吴 名
(中国航天科工集团8511研究所,江苏南京 210007)
0 引言
空间电子侦察作为情报获取的重要手段,具有陆基、海基、空基等平台不可替代的优势,在军事领域一直占有很重要的地位。双星时频差定位系统通过测量得到同一辐射源到达主副星的到达时间差(TDOA)和到达频率差(FDOA),就可以对地球表面辐射源的位置进行估计。时频差定位体制相对于单星测向体制而言,定位精度更高,在通信信号的电子侦察中已经发挥着重要作用。雷达脉冲信号是一类非常重要的侦察目标,由于单个脉冲的持续时间短,难以得到高精度的频差测量结果,故如何实现雷达信号的频差高精度估计一直是研究的热点和难点。
互模糊函数是实现时差与频差高精度估计的一种有效手段。时差与频差的测量精度与积累时间成正比,要得到高精度的频差估计结果,需要进行多脉冲联合处理,数据量巨大,同时雷达信号一般是宽带信号,侦察接收机的采样率通常在百兆级别,中频采样数据巨大,对星间、星地链路和接收机的处理能力都有较高的要求。这些因素都限制了时频差体制在雷达信号侦察中的工程应用。
国内多家单位开展了雷达信号时差频差定位体制研究,已经取得了初步进展。文献[1]提出了一种分段计算互模糊函数的方法,大大减少了相关处理的计算量;国防科大在此基础上创新性地提出利用相位谱进行频差估计的方法,该方法无需传输中频数据,极大地缩小了星间数传的压力,使得频差估计向实际工程应用迈出了一大步,算法也得到原理样机的验证,可以对雷达信号实现赫兹级别的频差估计精度。但是,双星时频差体制在雷达信号侦察工程应用中,还存在着时频差模糊、频差快速变化补偿、同型多目标配对以及适应复杂调制信号等关键问题亟待解决,本文针对以上问题展开重点讨论。
1 时差频差测量定位
双星时频差体制是利用2颗卫星测量地/海面辐射源信号到达各颗卫星的时间差和频率差来实现定位的。其基本的原理是:由于地面辐射源相对2颗卫星的径向距离不同可以得到一组时差,确定一个时差曲面,地面辐射源相对2颗卫星的径向速度不同可以得到一组频差,确定一个等频差曲面,从2个曲面与地球表地面的交点就可以获得地/海面辐射源目标的位置信息,如图1所示,其中另外一个交点为镜像模糊点,需要采用其他手段进行剔除。
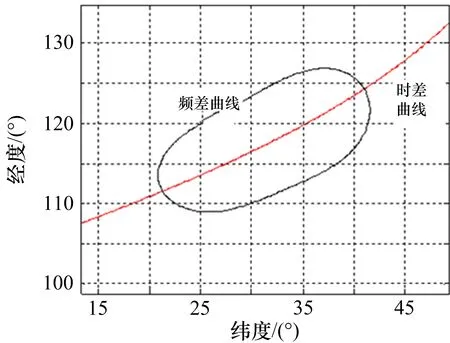
图1 时频差定位二维几何示意图
雷达信号的时差测量可以考虑2种实现方法。第一种,通过测量脉冲的上升沿得到脉冲到达时间(TOA),然后两者相减得到时差(TDOA)。目前工程上已经可以实现数十纳秒的时差测量精度。第二种是采用相关的方法,信号的x(t)和y(t)的相关表达式为:
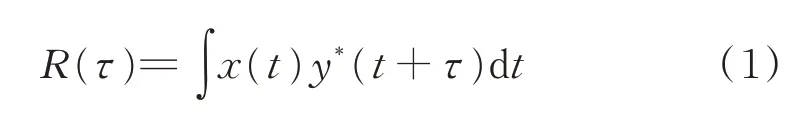
检测相关函数R(τ)的峰值就可以提取时差。相关法得到的时差精度与积累时间、信号带宽相关。
雷达信号的频差测量也可以考虑2种实现方法。第一种是间接法,通过测信号的到达频率(FOA),两者相减可以间接得到同一辐射源信号到不同接收机的多普勒频差(FDOA)。由于单个脉冲的持续时间短,单个脉冲FOA的测量精度最高在千赫兹级别,不能满足定位的需求,要达到赫兹级别的测量精度需要进行多脉冲积累,多脉冲积累存在FOA测量模糊问题,同时该方法对非相参雷达信号不适用。第二种是直接法,采用互模糊函数实现对频差的高精度估计,假定主副星接收信号为s1(t)与s2(t),则两者的互模糊函数(CAF)[2-3]为:
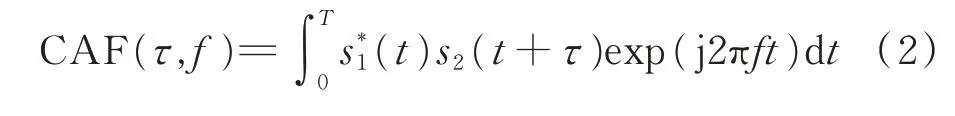
式中,T是相关积累时间。CAF(τ,f)是关于时延τ和多普勒频偏f的二维函数,找到|CAF(τ,f)|的最大值就可以实现对时差与频差的联合估计。利用互模糊函数对时差和频差的估计精度与信号的累积时间相关,积累时间越长,时差频差估计精度越高[4]。
目前已有的相位谱估计频差的方法就是利用互模糊函数实现的。文献[5]给出了一种分段计算互模糊函数的方法,将积累时间T的互模糊函数分成M段,对一段分别计算其互模糊函数,再将M段的互模糊函数进行相干累加,等效于积累时间为T的互模糊函数,分段相干累加的公式为:
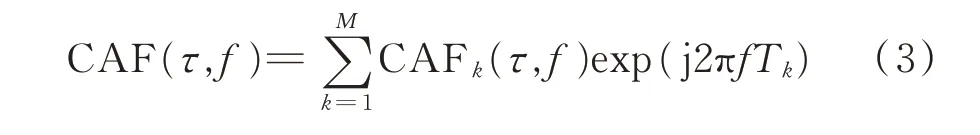
式中,exp(j2πfTk)为相位校正项,Tk表示第k段与第1段的时间差。
因为将分段过后的数据进行累加时,积分上下限会改变,这会对积分内的相位加权值ej2πft造成影响,所以对各子段的CAF进行相干累加时,需要对每一段的CAF做相位补偿,消除由各段信号在不同积分时间下造成的相位偏差。
针对雷达信号,M可以表示成积累时间T内的脉冲个数,Tk表示第k个脉冲与第1脉冲的时间间隔,在无源场景下,Tk只能由估计的TOA相减得到。CAFk(τ,f)表示每个脉冲的互模糊函数,可称为子互模糊函数。CAF(τ,f)可称为总互模糊函数,由多个脉冲相参积累得到。
互模糊函数的计算有时域和频域2种形式。式(2)是时域表达式,对于每个脉冲的互模糊函数的频域表达式为:
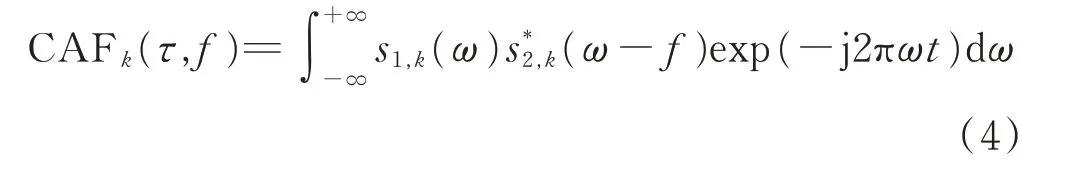
式中,s1(ω)和s2(ω)分别是s1(t)与s2(t)的傅里叶变换。
从信号能量的角度看,s1(ω)的有用信息只在峰值附近的几个频点内,其他都是无效点。故在进行谱相关处理时,只利用峰值附近的几个有效点就可以实现互模糊函数的计算。对于星载系统的实际应用,只需传输峰值附近几个点的相位谱信息,无需原始中频数据就可以实现对脉冲信号的频差估计。
2 时差频差模糊分析
由于雷达信号在时域上具有稀疏性和周期性,利用互模糊函数进行时频差联合估计时会存在多个峰值,如图2所示,会造成时差与频差估计模糊。对于重频固定的脉冲信号,时差的模糊周期为脉冲重复间隔(PRI),频差的模糊周期为脉冲重复频率(PRF)。
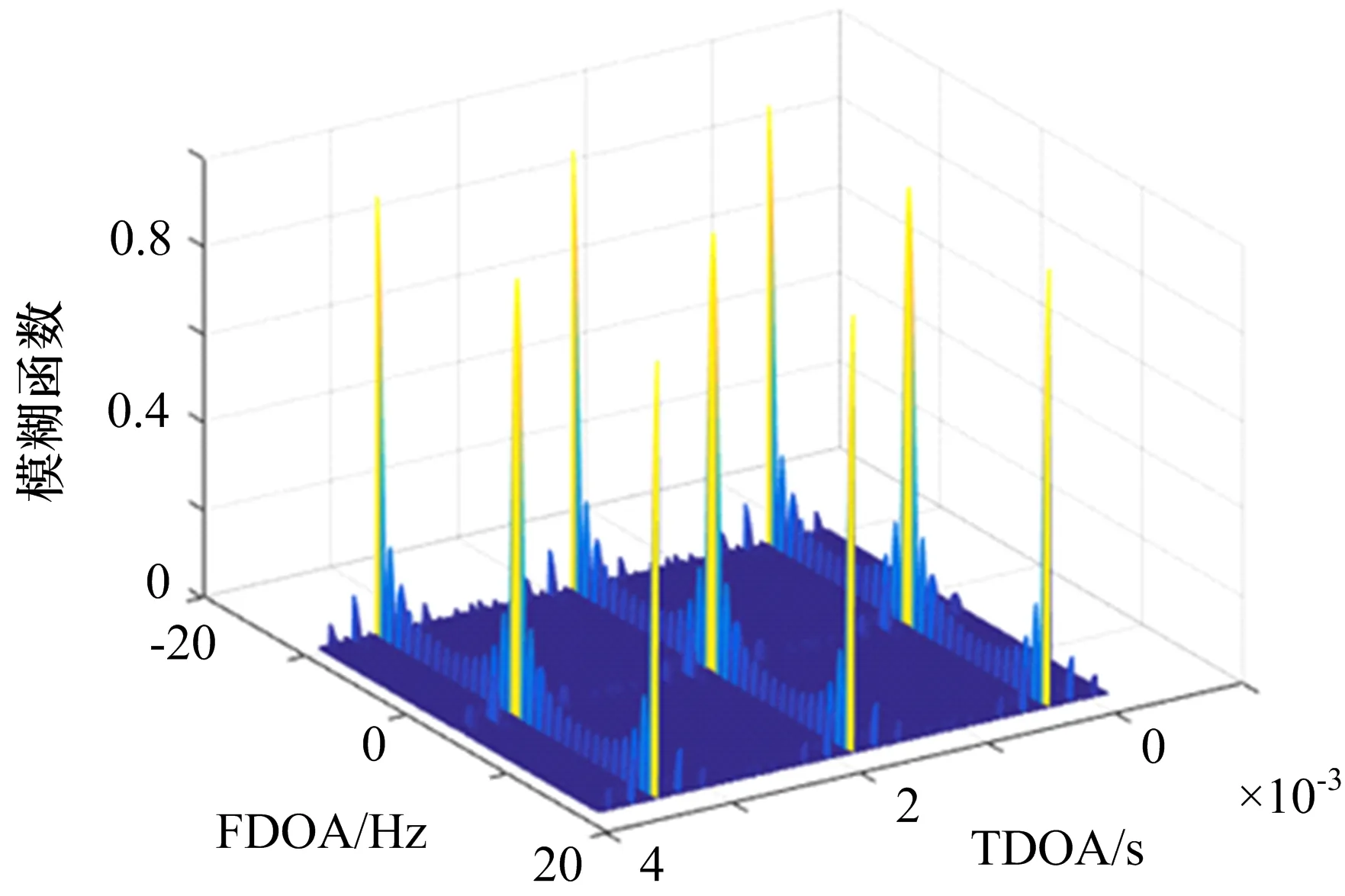
图2 雷达脉冲信号的互模糊函数图
时差模糊主要与雷达脉冲信号的脉冲重复间隔有关。如果在卫星的侦察区域内,时差变化区间大于脉冲重复间隔,则可能存在时差模糊[6]。时差模糊的必要条件是:

式中,TDOAmax为卫星侦察范围内最大的时差,TDOAmin为卫星侦察范围内最小的时差。[TDOAmin,TDOAmax]可称为时差配对窗口,通常采用时差模糊数nTDOA来评价时差模糊的程度,其中[·]为取整符号:
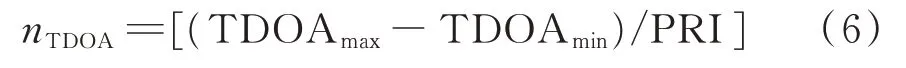
故对于低重频信号,时差模糊数nTDOA很小,甚至不发生模糊,而高重频信号的时差模糊数nTDOA比较大,时差模糊程度比较严重。而对于一些PRI具有特殊调制的,例如重频参差、重频滑变的,时差模糊周期是其骨架周期,模糊数nTDOA相对较小,所以这类信号更不易存在时差模糊现象。
频差模糊与雷达脉冲的重复频率相关的,如果在卫星的侦察区域内,频差变化范围大于脉冲重复频率,则可能存在频差模糊。频差模糊的必要条件是:
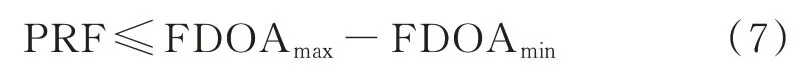
式中,FDOAmax为卫星侦察范围内最大的频差,FDOAmin为卫星侦察范围内最小的频差。[FDOAmin,FDOAmax]可称为频差搜索区间,通常采用时差模糊数nFDOA来评价频差模糊的程度,其中[ ]为取整符号:
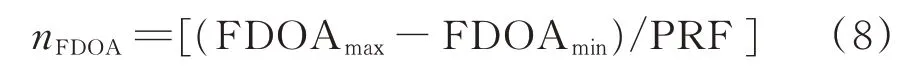
故对于高重频信号,频差模糊数nFDOA很小,模糊程度小,而低重频信号的频差模糊数nFDOA比较大,频差模糊程度比较严重。
现有解决时频差模糊问题的方法一般都是借助其他手段提供辅助信息,缩小时差的配对窗口和频差的搜索区间,从而将时差模糊数nTDOA和频差模糊数nFDOA降为1,即不存在模糊。针对时频差模糊问题,文献[7]提出了利用时差序列得到频差的粗估计值,然后在粗估计值的±3σf范围内进行频差搜索,缩小了频差的搜索区间。文献[8]在此基础上,利用频差与频差变化率对目标进行定位,找到与目标定位结果反推得到的时差最接近的时差值作为时差的估计值,达到解时差模糊的目的,但是对于雷达脉冲信号而言,频差变化率观测量较难获取,在工程上难以应用。
本文继承上面的研究成果,提出一种利用干涉仪解决时频差模糊的方法。先利用干涉仪测角得到目标的初始位置,结合卫星的位置和速度信息可以得到该位置的时差'和频差',在区间进行时差配对和区间中进行频差搜索。其中σt和σf是单星测向定位误差决定的,测向误差越小,σt与σf越小,故只要保证3σt<0.5PRI和3σf<0.5PRF,时差模糊数nTDOA和频差模糊数nFDOA就能降为1,就解决了时差与频差模糊问题。
3 频差快速变化补偿分析
在星载侦察中,由于卫星相对目标的运动不固定,是一个时变的过程,故频差也是时变的,其变化的快慢程度与目标相对卫星的加速度有关,而且频差估计是一个长时间积累的过程,随着积累时间的推移,频差相关峰会发生展宽,甚至分裂,并且峰值的幅度会降低,从而带来相关积累损耗,导致频差参数估计精度较低。对于时变频差的补偿关键在于通过一些辅助手段获得目标相对卫星的加速度信息,利用加速度信息将变化的频差补偿成固定的频差,时变频差的补偿公式为[9]:

式中,a为目标相对2颗卫星的加速度差。对于加速度信息的获取有如下几种方法:1)利用干涉仪测向的定位结果,计算该定位点相对卫星的加速度;2)利用短时间的积累获得的频差估计值进行时频差定位,并利用定位结果计算该位置点相对卫星的加速度。
补偿前后时变频差的估计如图3所示。
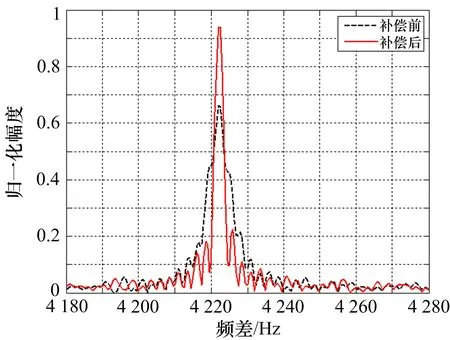
图3 补偿前后时变频差的估计
4 结束语
针对时频差体制应用于雷达信号侦察的一些工程实现问题,本文对时频差测量方法、时频差模糊、时变频差的补偿展开了详细分析,并对这些问题都提出了相应的解决措施,部分技术已经过试验的验证。除此之外,对捷变频信号的频差估计、同型多目标配对问题也进行了研究。不过时频差体制在实际工程应用时还有很多问题值得深入研究,如星上脉冲丢失严重、脉冲幅度起伏、混入干扰信号和干扰脉冲、干涉仪体制与时频差体制如何最优结合等,这些问题都是未来研究的重点。

