基于速率先验信息的固定单站仅测角目标运动分析*
张文俊,张 敏,马劲博,柳 征
(国防科技大学电子科学学院,湖南长沙 410073)
0 引言
无源定位系统是通过接收辐射源发射的电子信息进行定位,这种定位方法具有作用距离远、隐蔽性好等优点,对提高电子战系统在战场环境下的生存能力和作战能力有着重要作用。无源定位技术可按观测站数量分为单站和多站无源定位系统,多站无源定位系统可获得的信息量大、定位精度高,但要求能对目标共视,选址难度大,布站成本高。单站无源定位系统选址方便,布站成本低,且避免了多站定位要求站间同步和大量数据传输等问题,成为了定位跟踪研究领域中的热点。
固定单站仅测向定位方法对运动目标不具有可观测性,现有定位方法需在仅测向的基础上增加相位差变化率、多普勒频率变化率等观测信息。但是在实际应用中,多普勒频率变化率、相位差变化率等参数的测量精度要求高,系统相对复杂。
在实际环境中,目标的种类有限,且由于安全和经济等因素,目标通常进行匀速巡航,并且速率可以通过资料获得。若在速率先验信息的基础上通过仅测角实现对目标的定位跟踪,对充分挖掘单站效能、拓宽定位范围具有重要意义。本文探讨如何利用目标数据库中的速率先验知识进行定位跟踪,提出基于速率先验信息的固定单站仅测角目标运动分析算法,进行了数字仿真,并对结果进行分析。
1 基于速率先验信息固定单站仅测角跟踪建模
在运动分析中,目标的巡航状态通常以匀速直线运动模型来描述。如图1所示,以观测站为原点O,正北方向为Y轴,正东方向为X轴,辐射源与固定观测站连线与Y轴的夹角为观测角,取顺时针方向为正。初始距离为r0、初始时刻角度为β0、航向为α、速率为v。由于空间目标都可以完全限制在其航迹与观测站所组成的平面上描述,所得结论可推广到三维空间中去。
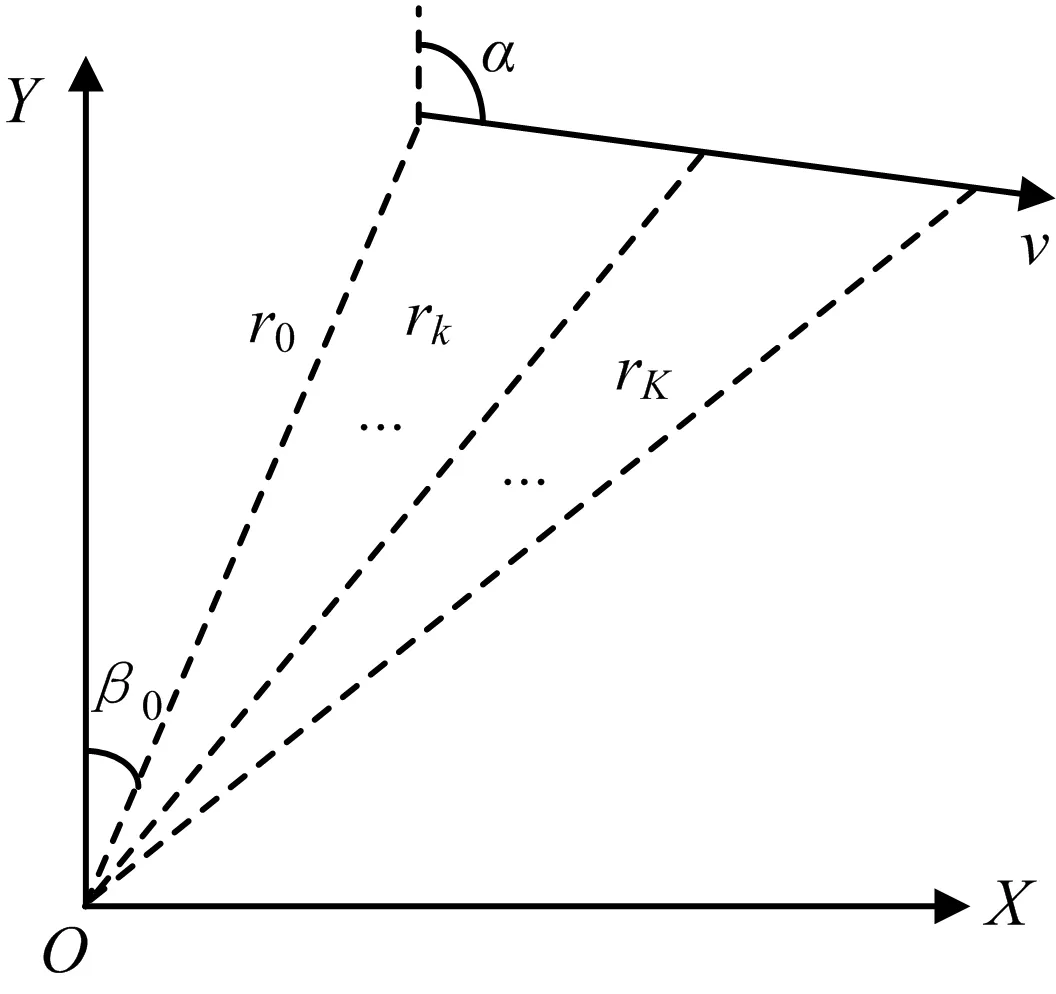
图1 匀速运动辐射源运动场景示意图
1.1 状态模型
假设观测站位于xO=[ 0 0 ]T,辐射源做匀速直线运动,定义其状态为:
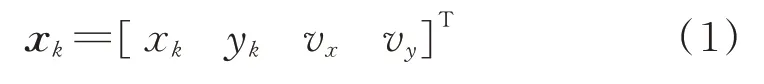
假设辐射源的速率v已知,而辐射源位置[xk yk]T和航向α未知,则上式进一步可修改为:
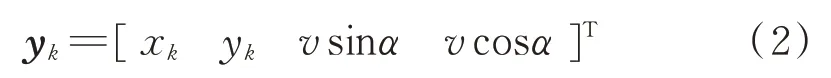
可以得到状态方程为:
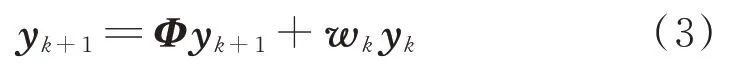
式中,wk为过程噪声,状态转移矩阵为:
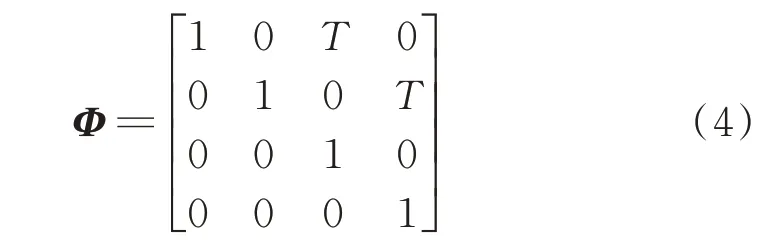
由式(3)和式(4)可知,k时刻的辐射源位置可由初始时刻的状态表示:
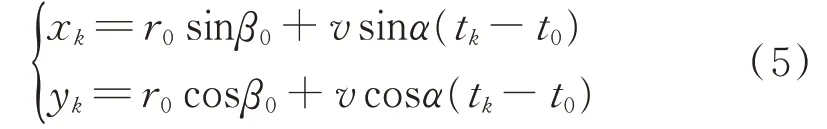
式中,t0、tk分别为初始时刻、观测时刻,r0为辐射源到目标的初始距离,β0为初始时刻角度,α为航向,v为速率。初始时刻角度β0可以通过测向设备得到,而辐射源速率v信息假设通过先验信息获得,因此只需将初始距离r0、航向α作为待估计量,分析辐射源的运动状态。
1.2 观测模型
二维条件下方位角的测量方程为:
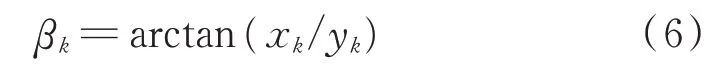
2 可观测性分析
2.1 可观测性分析原理
可观测性概念是卡尔曼在20世纪60年代首先提出的,表征系统状态能否由其输出完全反映的问题。若能根据观测区间内的量测信息唯一地确定出目标状态集合Xt=[xt yt vxt vxt]T,则可完整地描述出目标的运动轨迹,进而实现对目标的定位与跟踪。因此仅测角目标运动分析的可观测性问题,就是在仅有目标方位量测信息β=[β0,β1,…,βk]的条件下,目标状态参数解的存在性与唯一性问题。
如图2所示的辐射源运动例子中,目标的2种运动轨迹对应的方位角观测值完全相同,因此仅利用测角信息不能确定辐射源的位置。
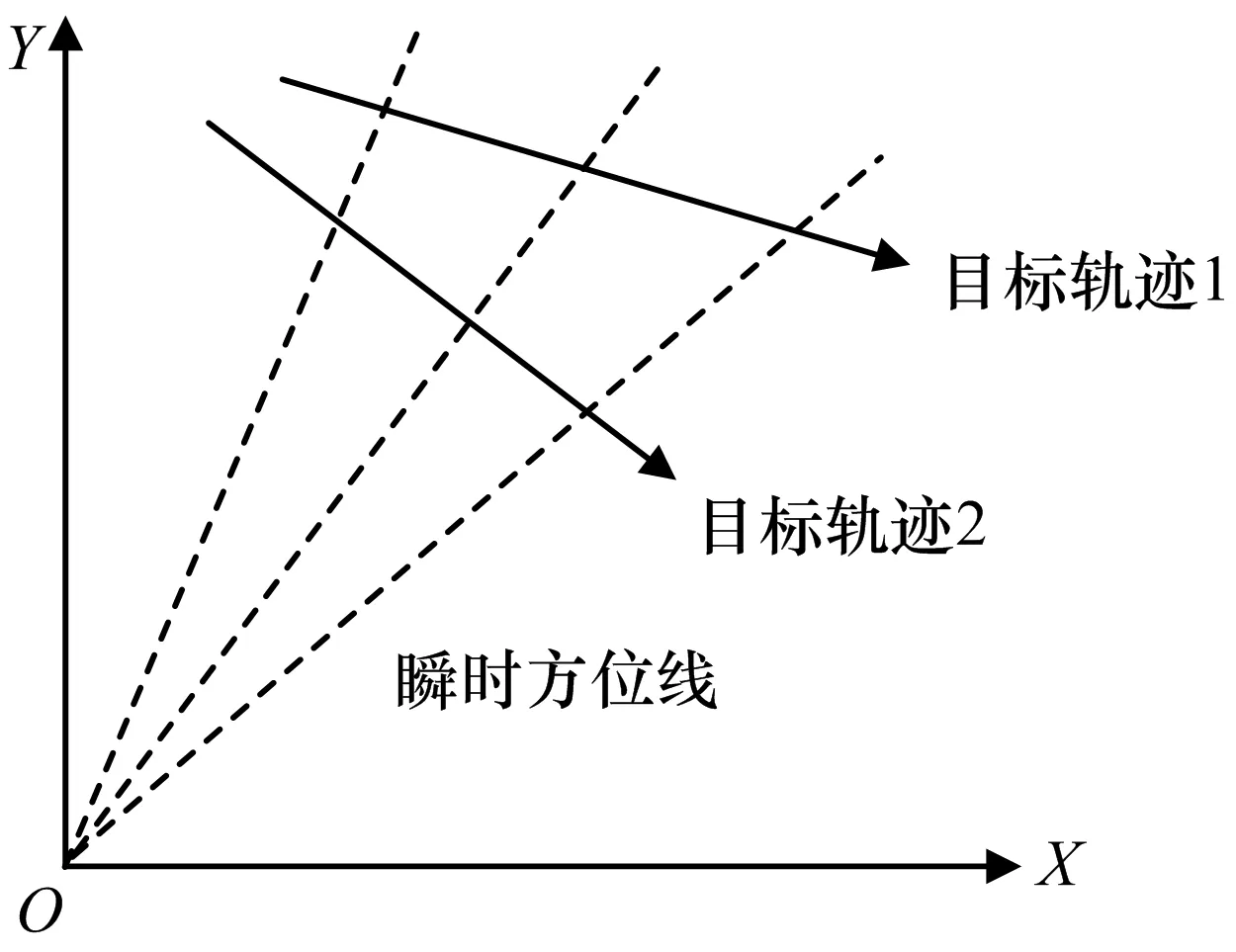
图2 一种仅测角定位不可观测时的目标轨迹示意图
当观测方程是非线性时,根据Lee和Dum等人所提出的可观测性定理,状态定义为:
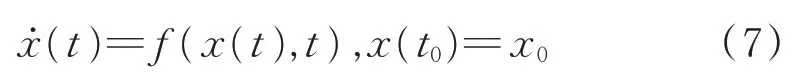
输出定义为:
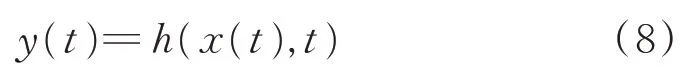
如果对于凸集S∈Rn上的所有x0,都有:
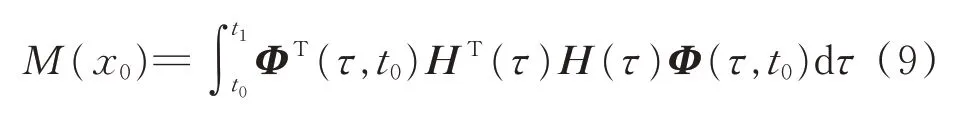
是正定的,则系统在S上是完全可观测的。其中H(τ)=∂h(x,t)/∂x,Φ(τ,t0)是∂f/∂x的转移矩阵。对离散系统,考虑利用观测序列Zi+n-1={zi,zi+1,…,zi+n-1}来确定系统在i时刻的状态Xi,则对于初始集合S中的n维矢量,记:
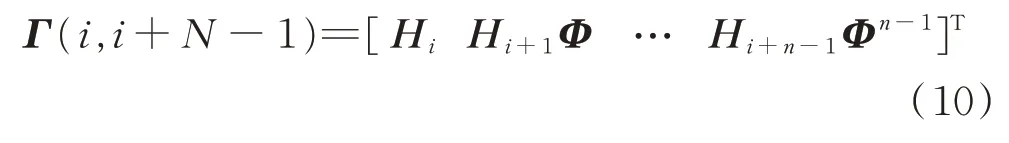
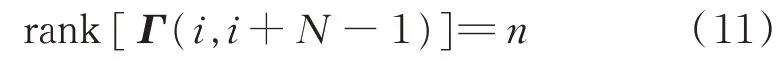
则系统在S上是完全可观测的。
2.2 基于速率先验信息固定单站可观测性分析
考虑在仅测角的基础上加入速率先验信息,对观测方程进行伪线性化处理可以将观测方程转化为线性形式,不考虑量测误差,由式(5)和式(6)可知,当k=1,2,…,k,k≥2有如下的方程成立:
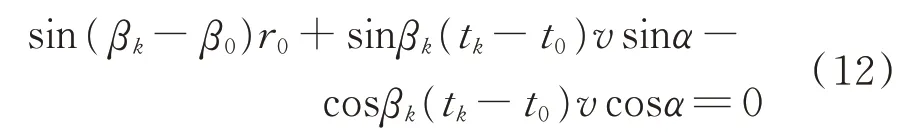
将等式右边分子分母分别除以r0可得:
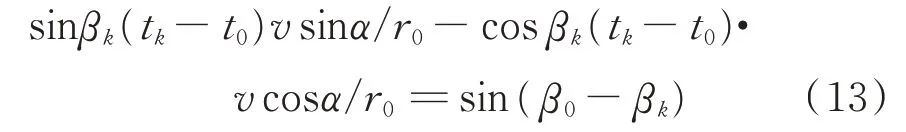
用矩阵形式可表示为:
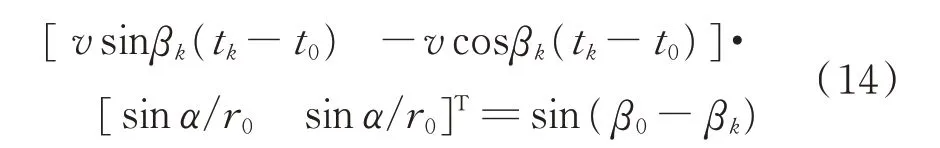
定义伪观测矩阵:
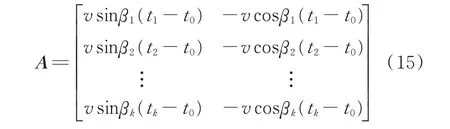
令M=ATA,则有:
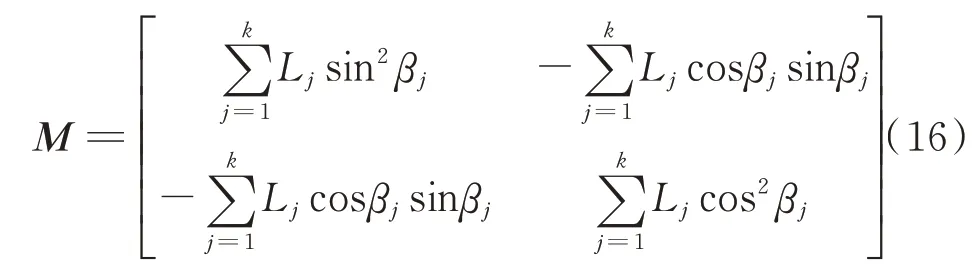
式中,Lj=v2(tj-t0)2,经推证M的行列式值为:
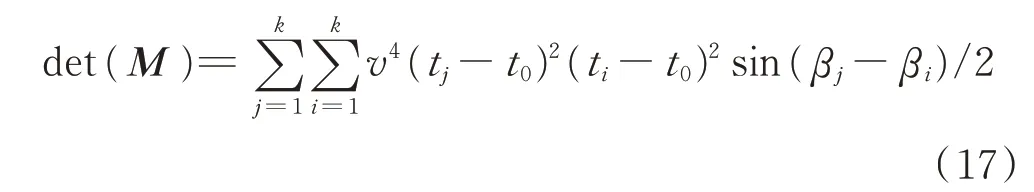
对上式分析可知,当k≥2且βi≠βj,i,j=1,…,k,有det(M)>0,则[sinα/r0cosα/r0]有唯一解,即可解得唯一的r0和α,即系统是可观测的。
3 已知速率先验的目标运动分析算法
3.1 伪线性估计方法
利用角度和速率先验信息,估计运动辐射源的初始距离r0、航向α。
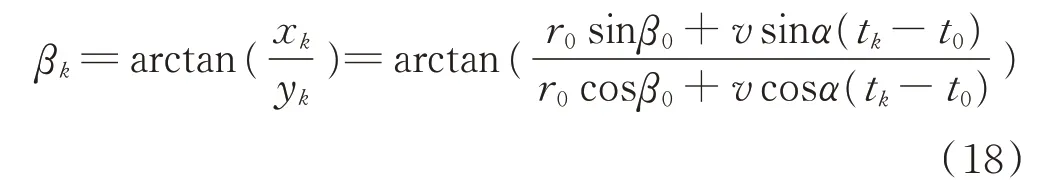
不失一般性,假设等时间间隔T获得角度观测量,即有:

进而可得:
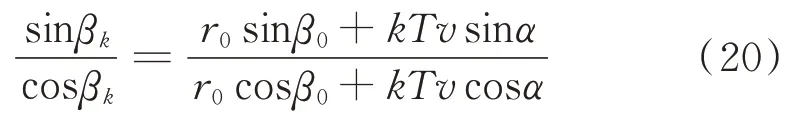
整理可得:
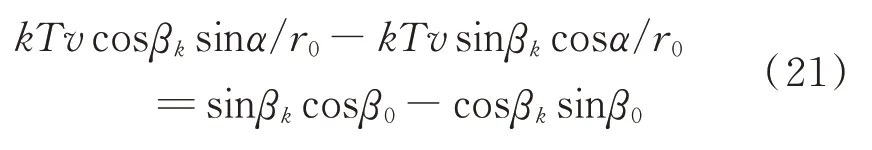
将sinα/r0和cosα/r0作为待估计量,并将K组观测量写为矩阵形式可得伪线性观测方程:

式中,
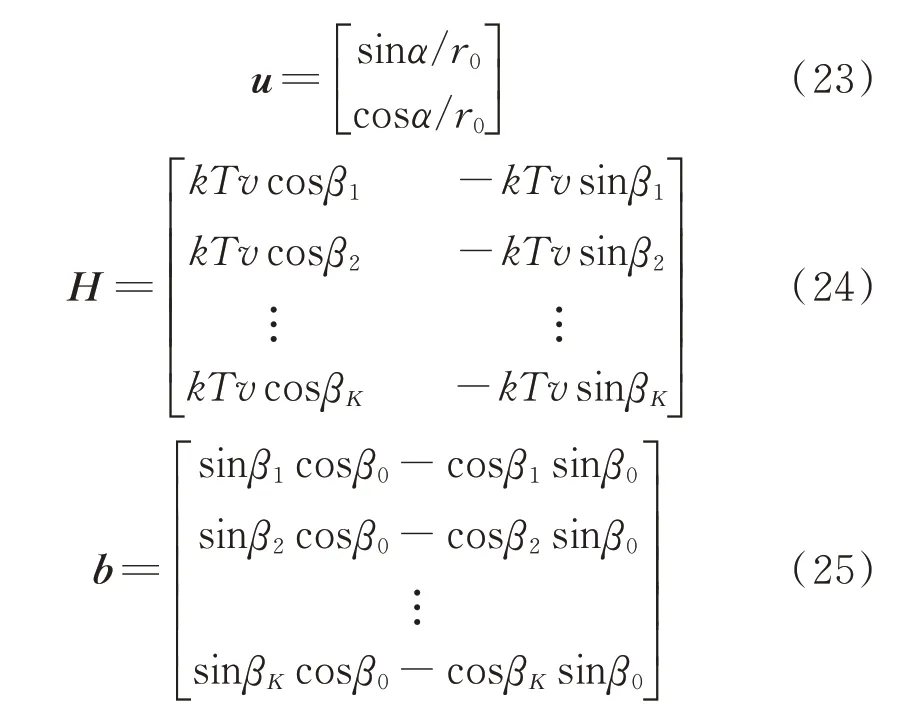
利用最小二乘可得:
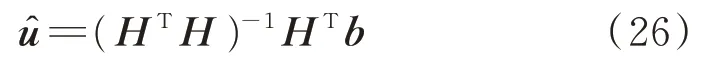
从而得到辐射源的初始距离和航向的估计值为:
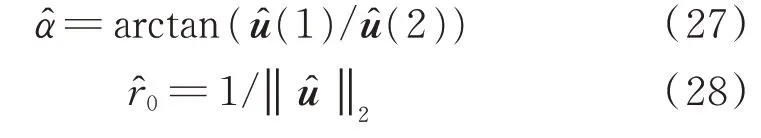
3.2 加权伪线性估计方法
为了减小估计误差协方差,可以选取合适的加权矩阵的改善伪线性估计的估计性能。对式(21),将βk利用βk+Δβ代入,并取一阶近似可得:

式中,εβ是由于角度测量误差引起的方程式误差,P=diag[r1/r0,r2/r0,…,rN/r0],diag[ ⋅]表示以向量为对角线元素构建矩阵。
可取加权矩阵:
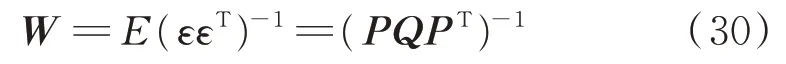
由于加权矩阵中包含目标初始距离和航向,而事先无法得到,因此首先利用下式进行计算:

4 CRLB分析
在基于速率先验信息的固定单站仅测角目标运动分析中,影响定位精度的因素包括角度测量误差、速率误差等。假设观测序列为β,测量误差为零均值高斯分布且互不相关,方差为,误差协方差矩阵为E(ΔβΔβT)=Qβ,式中,Δβ=β-β0,β0为未知观测角真实向量。速率为v,方差为将辐射源的初始距离r0、航向α以及速率的真实值v0表示成一个未知向量φ=[u,v0]T,u=[r0α]。将角度的量测和速率先验表示成测量向量κ=[βT,v]T,于是量测的概率密度函数(PDF)的对数为:
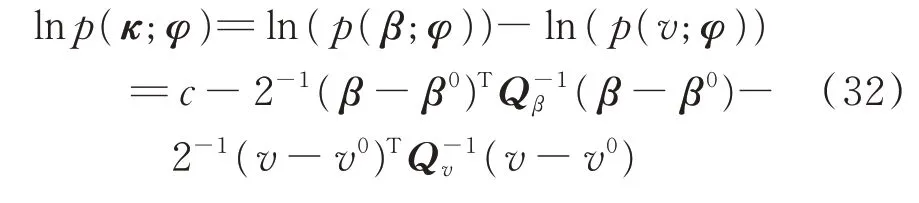
式中,c是与未知参数θ无关的常数,Qv是速率的误差协方差。
根据文献[6],未知参数φ的CRLB的计算方法为:
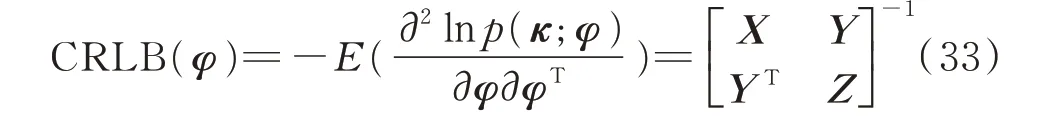
式中,
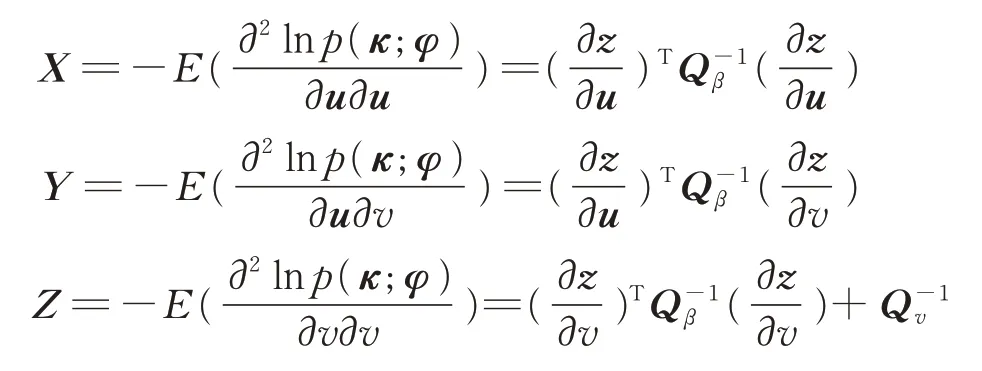
可得:
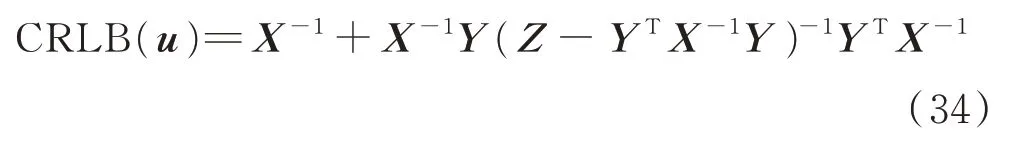
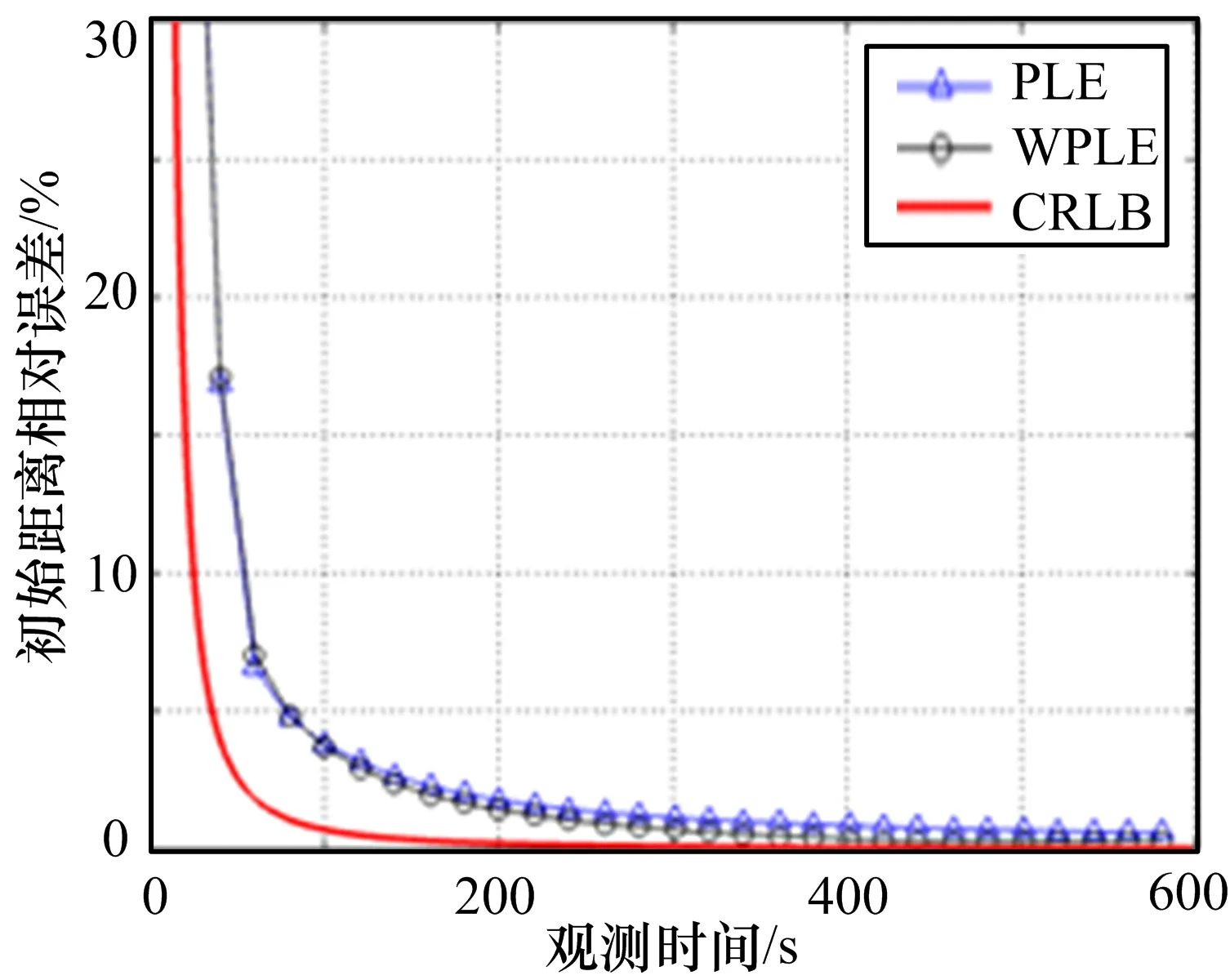
图3 定位结果(测向误差0.1°,速率偏差0%v)
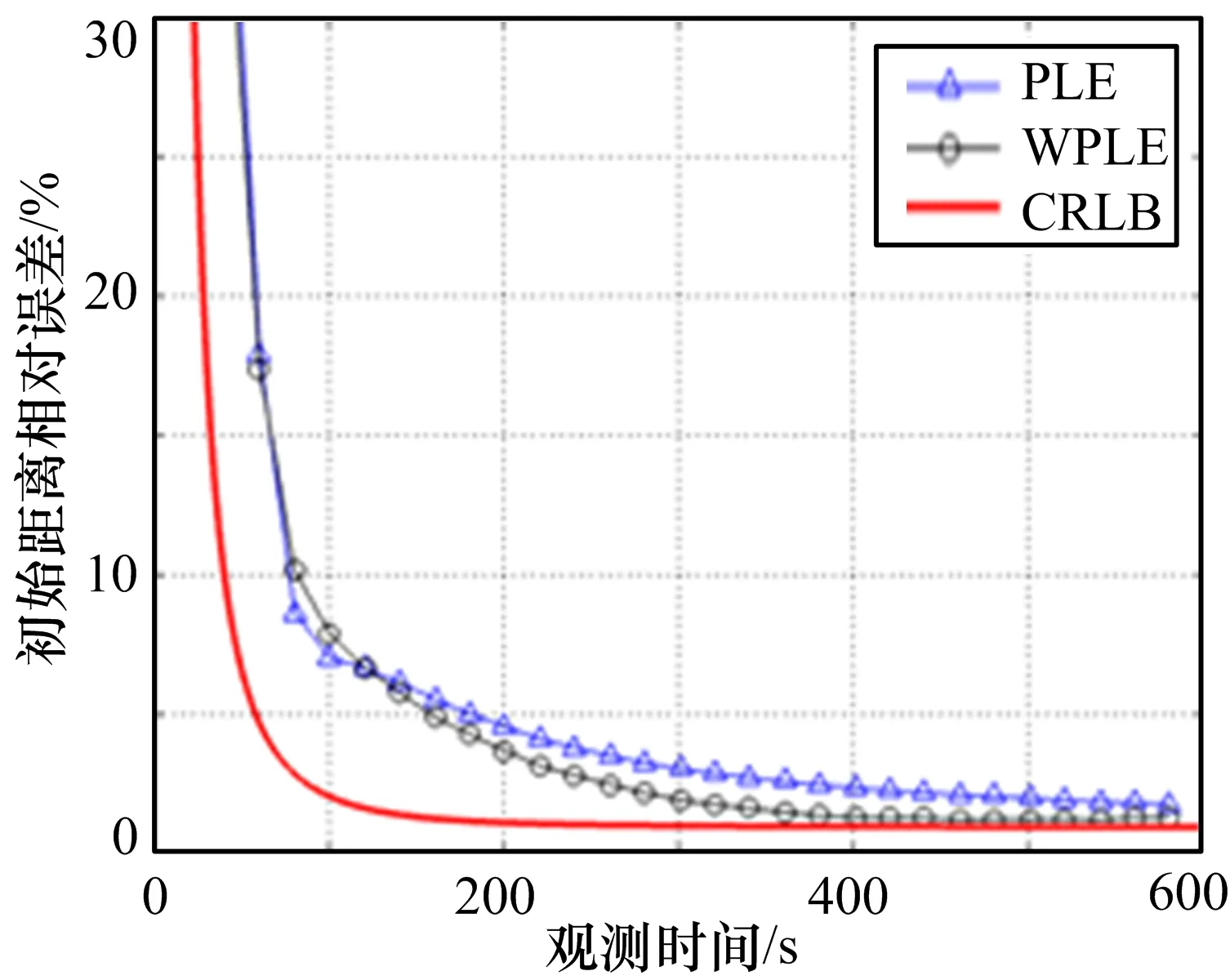
图4 定位结果(测向误差0.25°,速率偏差1%v)
式(34)为当存在角度测量误差和速率先验误差时的定位误差CRLB,其中X-1表示不存在速率误差时的定位误差CRLB。
5 仿真分析
本节通过仿真实验验证上述理论。仿真总时长为600 s,采样间隔1 s,固定观测站位于原点位置,辐射源初始时刻位置为(10 km,100 km),运动速率为250 m/s,航向为90°,辐射源与固定观测站连线与正北方向的夹角为观测角。Monte-Carlo仿真次数200次。仿真结果展示在图3-6中。
图3-6分别为不同测角误差与速率偏差情况下的定位结果。由实验结果可以得出,固定单站在基于速率先验信息的条件下通过仅测向即可实现对匀速直线运动辐射源的定位跟踪。伪线性估计(PLE)和加权伪线性估计(WPLE)方法的均方根误差都能达到CRLB,且WPLE方法的收敛速度更快,在测向误差和速度偏差较大的条件下仍能快速收敛。

图5 定位结果(测向误差0.5°,速率偏差5%v)
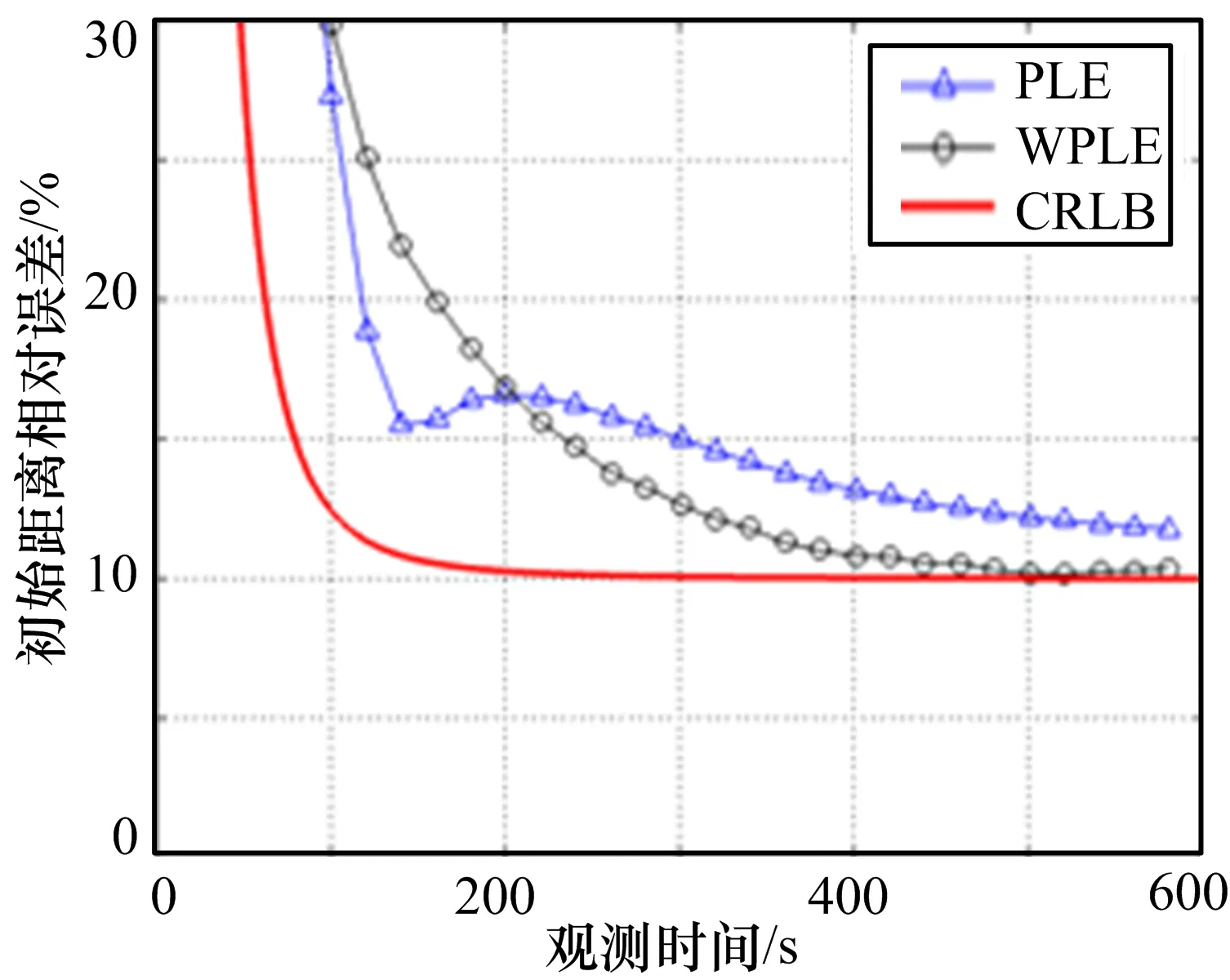
图6 定位结果(测向误差1°,速率偏差10%v)
6 结束语
本文研究了二维场景下,固定单站对已知速率先验的匀速直线运动辐射源目标的仅测角目标运动分析方法。有效利用了目标巡航速率固定且易获得这一特性,提出了基于伪线性估计和加权伪线性估计的目标运动分析算法。仿真实验表明,本文提出的方法可以较准确地实现对匀速率直线运动目标的定位跟踪。综上所述,本文算法原理简单,对参数的要求少,无需初值,相比现有算法具有更强的实用性。

