借力基本作图追溯“平行”之源
孟花维 邢成云

[摘要] 通过展示例题、分析考点,提出教学构想与定位,借助尺规作图法,运用逆向思维,在具体实施中使问题开放化,阐释不同思路下的解题方法,实现对初中学段相关平行判定知识、技能的统摄,进而建构起学生的数学核心素养。
[关键词] 尺规作图;问题开放化;逆向思维;平行的判定方法
一、呈现例题
下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程。
已知:如图1,直线l及直线l外一点P;
求作:直线PQ,使得PQ∥l。
作法:如图2,首先,在直线l上取一点A,作射线PA,以点A为圆心,PA长为半径画弧,交PA的延长线于点B;随后,在直线l上取一点C(不与点A重合),作射线BC,以点C为圆心,CB长为半径画弧,交BC的延长线于点Q;最后,作直线PQ,直线PQ就是所求作的直线。
根据小东设计的尺规作图过程,使用直尺和圆规,补全图形,并完成下面的证明。
本题是2018年北京市中考卷第17题,考查对象是尺规作图。本来过直线外一点作已知直线的平行线是基本作图,新的课标将此淡出了,而北京市以此为素材,编拟了这道以阅读理解为抓手的尺规作图题,很有创意。综观整个题目可以发现,它完整展现了尺规作图的一般步骤及过程:已知、求作、作法、证明,并填写作图依据。这是对2011年版课标提出的“作图要有根有据”的积极践行,也是一种方向性引领。“傅种孙强调几何作图是存在问题的变形,其依据为存在问题所本的公理体系,就性质而言,几何作图是几何事理的另一种表现形式,然其作图依据是几何事理。”[2]这段话揭示了几何作图的本质,给几何作图以功能定位。尺规作图不能仅停留在操作层面,更要弄清作图的因与果以及作图中的逻辑关联,而这已经在各地中考中有所体现,并有遍地开花之势。
二、教学构想与定位
若将本题定位于上述的题目分析或者说把这道题视为一道几何作图题目去解决,则其重心就落在了三角形“中位线”的平行功能探寻上,既窄化了基本作图方法,又在无形中削弱了作图本身承载的反扣知识、技法、思想观念等功能,其价值就大打折扣了。若以此题目的题干为项目,开展探究活动,就给学生的思维注入了活力,恰如杜威所言:“问题的冲击与刺激,使心智尽其所能地思索探寻。”这种心智活动趋向调节着学生思维的走向,如此一来,探寻平行之法的活动就启动了。
基于这些认识,笔者在课堂上引导学生展开了全方位的平行方法探寻活动。由于不单单朝向一个方法的解决,这就需要学生广泛搜罗,把作图与计算、证明、分析、判断等数学思维活动联结起来,对初中学段相关的平行方法通过作图这一动手与动脑联袂的实践活动实现凝聚,以期收到良效。
以上教学构想是朝向数学核心素养的建构活动,它融尺规作图、直觉判断、思维分析于一体。基于这样的定调,尺规作图就不仅仅是一种操作,更是对数学思维和數学探究过程的追溯。如其中用到逆推的方法,用目标图展开探索,引导学生先综合分析基本作图模型(数学建模),借力几何直观,预测、判断,积淀直观想象,通过逻辑分析,再进行画图操作,进而提升学生尺规作图的综合能力。因此,本题目的教学定位是以作图为载体,启迪学生思维,探根觅宗,通透原理,在灵活应用基本作图方法的同时,对初中学段有关平行的知识、技法进行应用性梳理,形成集成块,以达到系统化复习数学的目的。
三、具体实施
直接隐去作法及后面的内容,把问题开放化,引导学生去探寻不同的作法并给出作图依据,就能够放大本题的功能。具体教学时,可以让学生先行独立尝试,并鼓励学生多法求图,增加挑战性。学生通过自己操作直尺和圆规,在平行方法追溯的驱动下,激活自主思维,既能以“过直线外一点作平行线”为抓手,全面复习各类基本作图,又可以在逆向思维的作用下把初中学段相关平行判定的知识、技能来一个大盘点,发挥了尺规作图的统摄作用,促进了知识的内化,磨砺了思想方法的效能,进而提高了学生的核心素养。以下呈现课堂教学实践中师生对话与交流出来的方法,以期启发解题思路。
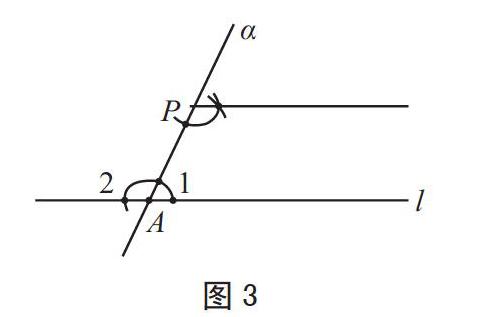
方法一:如图3,标出∠2,作角等于已知∠2。根据“同旁内角互补,两直线平行”或“内错角相等,两直线平行”,用到的是“作角等于已知角”的基本作图。
方法二:如图4,两次“过一点作已知直线的垂线”(第一次过直线l外点P作直线l的垂线AP,而后过点P作直线AP的垂线)。根据“在同一平面内,垂直于同一直线的两直线平行”(或根据“同旁内角互补,两直线平行”),用到的是“过直线上一点或直线外一点作已知直线的垂线”的基本作图。
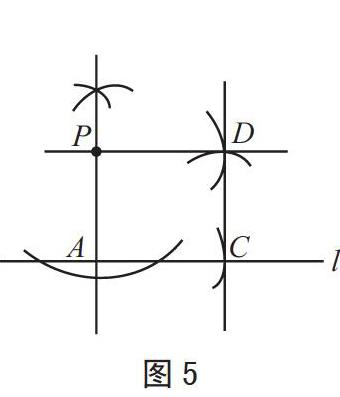
方法三:如图5,构造正方形,一次作垂线段(过直线l外点P作直线l的垂线AP),三次作相等线段(先行在直线l上截取AC=AP,再分别以点C、P为圆心,以AP为半径画弧,两弧交于点D,再过P、D作直线即可)。根据“正方形的对边平行”,用到的是“过一点作已知直线的垂线”和“作一条线段等于已知线段”的基本作图。
方法四:如图6,作射线PA交直线l于点A,以A为圆心、以AP为半径作⊙A交射线PA于点B,过点B作l的垂线交⊙A于C,则直线PC即为所求。用到的是“过一点作已知直线的垂线”的基本作图,根据“直径所对的圆周角为直角”和“平面内垂直于同一直线的两直线平行”。
最后,梳理方法及其原理,形成方法与原理的对接,把初中学段平行的判定方法凝聚起来。可见,以基本作图为基础,在反复历练的基础上,在尺规作图的实践过程中让学生体会到数学知识能够从不同角度加以分析,从不同层次加以理解,在知法明理的追溯中,增强学生的探究能力。
四、教后反思
尺规作图在描述“运动”、直观“操作”、问题证明等方面具有不可替代的价值。基谢廖夫的几何教科书特别注重尺规作图。无独有偶,著名数学家波利亚在《数学的发现》开篇章节就介绍尺规作图,这也从一个侧面说明了尺规作图在平面几何研究中的重要性。[3]2017年6月,代钦教授在中学数学课程与教材国际论坛上也指出“作图是几何教育的根基”。这些都给(尺规)作图以正名,厘定了作图的功用,便于教师施之以教,也给了命题评价以正确导向。以上的教学实践就是对这句话的实践性诠释,从中可以发现:尺规作图扎根于几何原理,关乎思维发展,连接着图形变换,是实现图形运动的强有力手段,是动手与动脑的和谐、融合,是一种深层次的“做中学”,是几何学习的有力助手。它对几何知识的理解有深化之用,凸显了思维张力及艺术魅力。
通过作图,学生可以把头脑中零散的概念和几何事实具体化、综合化、融通化,从而更深地领会几何定理的真谛。另外,它本身的约束力,它的理性与精致,自然增强了智能挑战性。“数学是思维的体操”是尺规作图的最佳注脚,它能统摄知识、固本结构、历练学生思维,是发展数学思维乃至理性精神的优质载体,是科学和艺术的完美结晶[4],可谓数学“真善美”的集中体现。
[参考文献]
[1]王亮亮.中考数学(北京卷)评价改革再述[J].数学通报,2018(10):48-52.
[2]张彩云,代钦.傅种孙几何作图思想探析[J].数学通报,2019(01):1-7,40.
[3]倪明,任念兵.俄罗斯再版基谢寥夫几何教科书给我们的启示[J].数学通报,2018(10):4-8.
[4]乐嗣康,崔雪芳,张奠宙.尺规作图教学的现代意义[J].中学数学月刊,2005(12):7-9.

