接触式轮廓扫描仪系统标定算法*
高 彤 ,陈 鸿 ,张 亮 ,王晋祺
(1.中北大学 电子测试技术重点实验室 仪器科学与动态测试教育部重点实验室,山西 太原030051;2.太原科技大学 交通与物流学院,山西 太原030051;3.上海无线电设备研究所,上海201109)
0 引言
现如今检测技术朝着精密、高效的方向不断提升,眼镜的生产和加工也向着高精度、自动化方向发展。 传统的方法需要定制相应的模板,工序复杂,耗时长,而且精度不高[1],不满足工业生产需求。 目前国内外普遍使用镜片自动磨边机,它是一种根据轮廓扫描仪所提供的轮廓数据进行自动加工镜片的设备,实现镜架凹槽或镜片轮廓参数的获取并传给数控磨边机从而实现加工全自动。测量轮廓的方式主要分为接触式测量和非接触式测量。 接触式测量利用扫描探针与被测物体接触,使扫描探针或被测物体旋转一周,实现对被测物体进行离散的空间点位置的获取,通过一定的数学计算,完成对所测数据点的分析拟合,最终还原出被测物体的轮廓;非接触测量有超声波法以及基于视觉技术的激光三角法、结构光法等[2-4],但利用光学的测量方式不适用于镜架凹槽。本文所研究的接触式探针扫描仪利用低压力接触式探针扫描镜架内凹槽或镜片边缘轮廓,其扫描原理就是利用检测探针接触被测物体一周的过程中得到旋转编码器返回的长度序列以及旋转平台的旋转角度来确定轮廓的坐标信息,编码器记录的长度是检测探针升起位置到被测物体轮廓边缘点的距离。 实际工程中,由于仪器零部件的安装不精准,检测探针的零点与旋转中心往往不重合,所以需要对得到的数据进行处理才能得到准确的曲线轮廓[5]。 对于此类系统误差问题,一般做法是对误差来源进行分析后,需要建立误差的精准数学模型,提出系统误差补偿或抑制方法[6-9]。 为了解决本文研究的问题,参考文献[10]提出的方法是对误差进行了精确建模,建立系统的误差数学模型,运用最小二乘法的基本原理求解最佳参数[10-12],但这种方法运算量较大,难以实现在线标定[13]。 本文提出一种利用尺寸已知的正方形标定板,通过测量标定板得到的数据来获取到系统参数,从而对被测物体的轮廓坐标进行在线标定。 并通过Qt Creator 软件编程模拟仿真了测量过程验证了算法的准确性。
1 扫描测量原理及误差产生原因
应用极坐标系下的构图原理,如图1 所示,以滑轨的初始位置为极坐标轴建立坐标系,坐标原点O 为检测钩升起的位置,旋转编码器记录由检测钩起始点到测量边缘点P 的长度ρ。 当检测钩所在的滑轨每旋转一个角度Δθ,则有与之相对应的长度序列。 实际测量中,只要能够获得被测对象轮廓一周无穷多个位置的坐标(ρ,θ),即可得到所需轮廓。
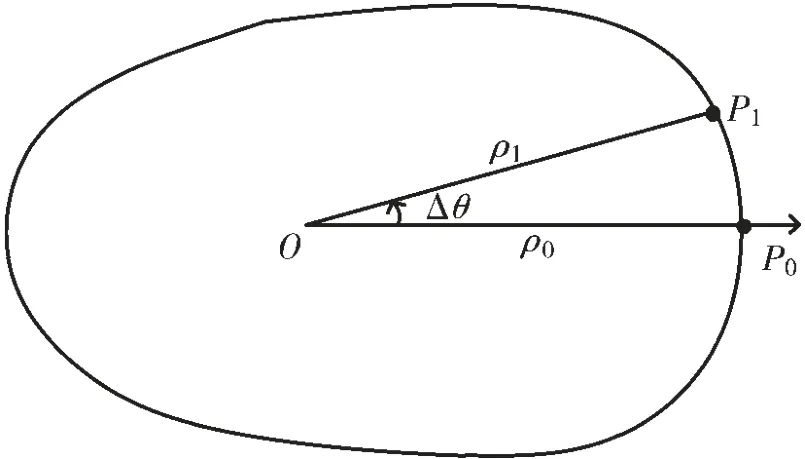
图1 测量原理图
误差产生原因:由扫描原理可知,测量点的起始测量位置须是一个定点,这样得到的数据才准确,而实际测量中由于扫描部件的安装会有偏差,导致检测钩的起始点与旋转中心点不重合,进而导致检测钩起始点在测量过程中是随旋转平台绕旋转中心而变化的,并非定点。 旋转中心到检测钩所在滑轨存在垂直距离,用这样得到的数据直接去拟合轮廓不可行,所以在正式测量镜框前需要对测量系统进行标定。
2 测量系统坐标标定算法
2.1 建立标定模型
建立合适的坐标系对于问题的求解非常关键,图2所示是将被测镜框固定在卡槽测量镜框镜圈。

图2 镜框/镜片扫描仪
为了便于说明测量结果及计算,建立如图3 所示的测量坐标系,其原点O 为旋转中心,两条坐标轴x 轴和y 轴的方向为卡槽的两组对边方向。 为了获取系统参数,这里采用带有4 个圆角的正方形标定板,将正方形标定板固定在卡槽内,标定板的边长方向与卡槽的两种组对边方向一致,将与第一条被测边长垂直的坐标轴定为x 轴正方向,按逆时针方向旋转;将与第二条被测边长垂直的坐标轴定为y 轴正方向。 Q 为检测钩起始点,M 为旋转中心到检测钩所在滑轨的垂心,P 为测量点。将QM 的值设为ΔL,OM 的值设为d。
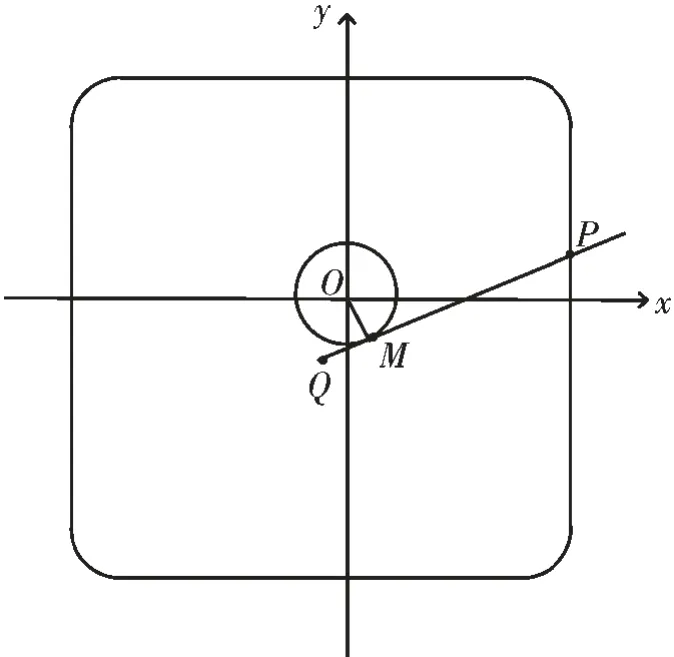
图3 测量坐标系
2.2 测量系统参数标定
下面选取一种位置情况进行说明,如图4 所示的参数标定模型中,设选取的一组极小值点的位置如图中的P0、P2。 测 量 点 是P0位 置 时,设 滑 轨 与x 轴 的 夹 角 为θ0,即∠OP0M0=θ0,其对边极小测量点为P2,设滑轨与x 轴夹角为θ2,即∠OP2M2=θ2。 在这里不作正负区分,本文规定从x 轴正半轴逆时针旋转而成的角为正角。

图4 参数标定模型
已知正方形标定板的边长L=45 mm,从测量数据可以确定O0P0以及Q2P2的长度分别设为ρ0和ρ2,从测量数据还可以确定滑轨由测量P0点逆时针旋转到测量P2点所用的旋转角度Δθ。 则可列出以下方程:

由 于sinθ0和sinθ2均 是 方 程(8)的 解,且 不 相 等,将 测量数据带入方程(8)解出sinθ0和sinθ2,带入方程(4)即可解得d。 从ρ0和ρ2的大小关系可以确定该方程的两个解 与θ0和θ2的 对 应 关 系,若ρ0>ρ2,则θ0<θ2,反 之θ0>θ2,从而确定θ0和θ2的值,将其带回式(1)或式(2)即可解出QM 的长度ΔL。
得到θ0和θ2的值后,再加上P0、P2在标定模型中的位置确定,即可确定检测钩在测量P0、P2点时滑轨与x轴正半轴的夹角。 图4 这种情况下,在测量P0点时,滑轨与x 轴正半轴的夹角就是θ0。 同理,如果选取的一组数据是P1、P3,得到滑轨在这两个测量点与y 轴的夹角θ1和θ3,则在测量P1点时,滑轨与x 轴正半轴的夹角为θ1+π/2。
设滑轨在初始位置与x 轴正半轴的夹角为α0,利用滑轨从初始位置逆时针旋转到测量极小值点的位置时的旋转角Δα,以及检测钩在测量该极小值点时滑轨与x 轴正半轴的夹角即可确定α0。例如测量极小值点是图4的P0点, 滑轨由初始位置转到测量P0点位置所用的旋转角为Δα,则α0=θ0-Δα。
2.3 测量系统坐标标定
获取到系统参数d、ΔL、滑轨在初始位置与x 轴的夹角α0后,即可对测量点P 的坐标进行标定。 如图5 坐标标定模型,要确定任意测量点P 的坐标,则需要确定OP与x 轴正半轴的夹角β 以及OP 的长度。 测量P 点时滑轨与x 轴正半轴的夹角α 可由α0和旋转角Δα 得到,则:
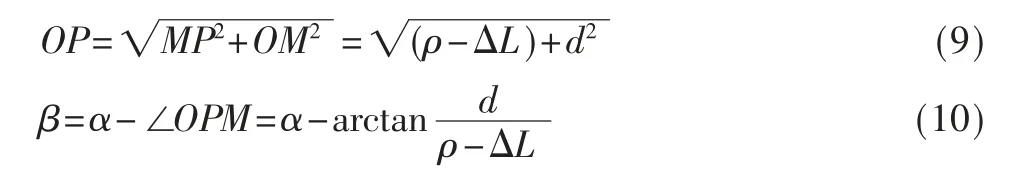
P 点的直角坐标由极坐标到直角坐标系下的转换即可得P(OPcosβ,OPsinβ)。
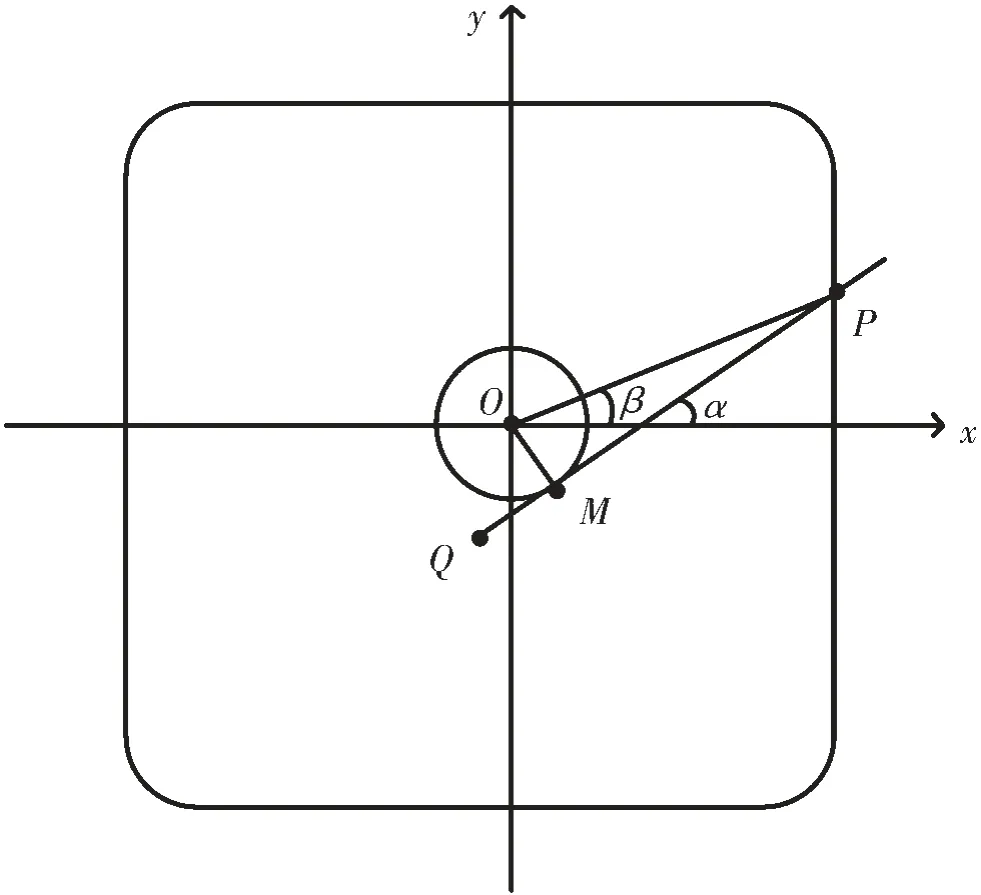
图5 坐标标定模型
3 测量数据处理
根据上述分析,测量正方形标定板的过程中如果采样点是连续的才会得到理想极小值点,即边长与坐标轴交点。而实际工程测量中采样点是离散选取的。提高采样点数可以提高取到理想极小值点的概率,本文所研究的接触式镜框扫描仪所能达到的角度分辨率最小为0.225°,即旋转一圈采样1 600 个点,在此分辨率下根据式(6)给定ρ、θ0后绘制Δθ 和d 的关系图,如图6 所示,显然0.225°的角度分辨率达不到系统要求的0.5 mm 精度。

图6 系统精度说明图
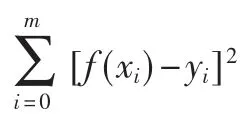
4 模拟仿真实验
为了验证标定算法,在给定正方形标定板、旋转中心与坐标系的相对位置关系后,利用Qt Creator 软件编程模拟仿真出在给定系统参数d、ΔL、α0下的数据。利用仿真出的数据用标定算法解出系统参数的值并于设定值进行比较,从而验证算法的准确性。
4.1 测量数据生成
当旋转中心和标定板的位置关系确定后,测量数据即可确定,与坐标系的位置无关。 这里仍然设旋转中心为坐标点(0,0),设旋转中心到垂心的连线与x 轴正半轴所成夹角为γ,系统的角度分辨率为φ=2π/n(n 为总采样点数),γ 的值可由系统角度分辨率和滑轨与x 轴正半轴的初始夹角α0确定,则滑轨运动到任意位置时,旋转中心到滑轨的垂心坐标为M(dcosγ,dsinγ)。 此时滑轨的斜率k=tan(γ-π/2),则滑轨所在直线方程确定,利用该直线方程与被测点所在的标定板轮廓曲线或直线方程联立可得测量点P 的坐标,求出M 点到P 点的距离再加上ΔP 即仿真出测量长度值ρ。
将四角带有圆弧(半径为r)的正方形标定板轮廓分为四部分,如图7 所示,分别为测量点从D0到D1、D1到D2、D2到D3以 及D3到D0。

图7 测量数据生成
当测量点位于D0到D1范围时,与切线方程联立的方程分为直线x=x1和y=y2以及圆[x-(x1-r)]2+[y-(y1-r)]2=r2,x1和y2已知。 设与两条直线联立解出交点坐标为P1(x1,y1)和P2(x2,y2),与圆联立解出两个交点坐标P3(x3,y3)、P4(x4,y4),M 点 与 这4 个 交 点 的 距 离 设 为d1、d2、d3、d4。 先比较d1和d2的大小,若d1<d2,则继续比较r 与y2-y1的大小,若y2-y1≤r,说明此时测量点位于圆弧上,否则测量点就是D1;若d1>d2,则继续比较r 与x1-x2的大小,若x1-x2≤r,说明此时测量点位于圆弧上,否则测量点就是D2。当测量点位于圆弧区段时,比较d3和d4的大小,较大的对应的为此时的测量点。 当滑轨运动到其他区段时测量点的选取过程同理。
4.2 测量数据拟合
模拟出测量数据后,绘制输出数据曲线波形图如图8所示。 对4 个极小值及周围采样点进行最小二乘法拟合,即设:f(x)=a2x2+a1x+a0。

对上述矩阵变换求解得到系数矩阵A[14-15],就得到了拟合曲线。

图8 输出数据波形图
4.2.1 采样点数目的选取
改变m 的大小得到不同的拟合函数计算出系统参数d,通过比较计算值与设定值的差值选择合适的m。将用于拟合的采样点数从5 到100 递增,得到系统参数d,绘制d 关于采样点个数的关系折线图,如图9 所示。若用于曲线拟合的采样点数过少,则会导致计算出的系统参数与理想值差距很大,故继续提高采样点数的起始设定值,如图10 所示,当采样点数选取在40 ~60 范围内,d 的计算值稳定接近设定值1.00 cm 且符合系统精度要求。

图9 d 关于采样点数的折线图1
改变正方形标定板与坐标系的位置关系后,经实验证明上述范围仍然适用。
4.2.2 拟合结果
将m 取为40,拟合结果如表1 所示,显然无论取标定板的哪组极小值数据去拟合,拟合后的数据均比拟合前的数据更接近设定值,且符合系统精度要求。
4.3 坐标标定结果
直接利用模拟得到的1 600 个测量数据绘制轮廓坐标点如图11(a)所示。 利用标定过的系统参数对正方形标定板的轮廓坐标进行标定后的结果如图11(b)所示,显然标定后的轮廓与真实轮廓接近。

图10 d 关于采样点数的折线图2
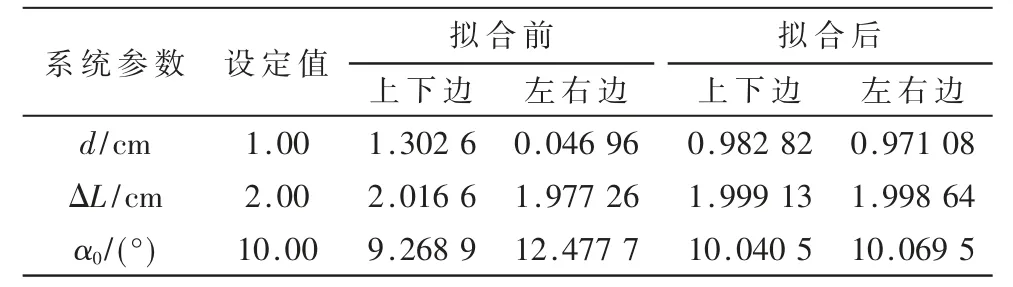
表1 拟合前后系统参数对比

图11 轮廓坐标图
5 结论
为解决轮廓扫描仪检测钩零点与旋转平台的旋转中心不重合造成的测量长度及角度误差,本文提出一种利用正方形的特点,通过测量正方形标定板得到的测量数据并经给最小二乘法拟合后计算出轮廓扫描仪的系统参数,进而对测量数据进行处理实现了坐标标定,还原出被测物体的真实轮廓。 并通过Qt Creator 软件编程模拟仿真了测量过程,用仿真出的数据验证了算法的可行性。 该方法大大降低了测量仪的制造和安装要求,通过在线标定即可快速测量被测物体轮廓且满足系统的精度要求,标定精度高而可靠。
——对2018年广州市一道中考题的研究

