双向内外管压差流量计关键参数优化
樊宝桐,孟 江,王 燕
(中北大学机械工程学院,山西 太原 030051)
1 引言
目前,在各种工业生产中流量的测量是非常重要的一部分,因此各种各样的流量计层出不穷,其中,压差类的流量计价格较低,使用的经验多,经过长时间的研究,精度越来越高,所以应用非常广泛[1]。
其中,双向内外管压差流量计具有对流体的扰动小和获得压差信号大的优点[2]。提出了压损差这一新的评价指标,在这些基础之上对节流件前后扩散角和细管的长度进行了优化,使其测量更加准确,对流体的扰动更小。
2 模型结构和理论基础
安装节流件的管道选择DN32 的管径。根据以往的研究,双向内外管压差流量计节流件的长度对流量计的性能影响不大,为了方便测量将节流件大管长度定为30mm,细管长度定为10mm。非对称双向内外管压差流量计的基本结构,如图1 所示。
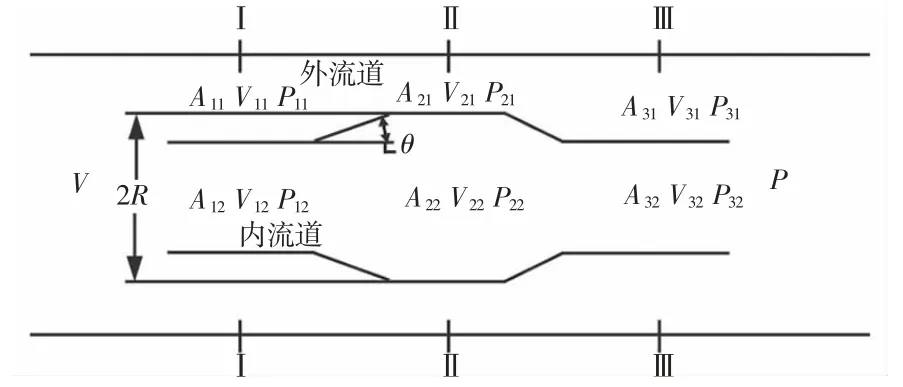
图1 流量计结构简图Fig.1 Flow Chart Structure Diagram
非对称双向内外管压差流量计的理论基础来源于连续方程和伯努利方程[3]。流体再通过节流件时,在Ⅰ—Ⅰ平面,外流道流体压缩节流,流速增大,压力减小,内流道流体则扩散,流速减小,压力增大;在Ⅱ—Ⅱ平面,内外流道比较平稳,流速和压力都趋于稳定;在Ⅲ—Ⅲ平面,与Ⅰ—Ⅰ平面情况相反,外流道扩散,流速减小,压力增大,而内流道流体压缩,流速增大,压力减小。如此一来,在Ⅱ—Ⅱ段内外就会形成最大的压差:

与传统压差类流量计的测量公式类似[4]流量Q的计算公式为:

式中:C—流出系数;
A—流道截面积;
λ—等效直径比;
ρ—流体密度。
流量计结构简图中A为流道的截面积,V为入口平均流速,P为出口压力。Amn、Vmn、Pmn中的m为 1 时,代表 Ⅰ—Ⅰ截面的参数,m为2 时,代表Ⅱ—Ⅱ截面的参数,m为3 时代表Ⅲ—Ⅲ截面参数,n为1 时代表外流道参数,n为2 时代表内流道参数,如图1 所示。根据伯努利方程,外流道和内流道分别有:
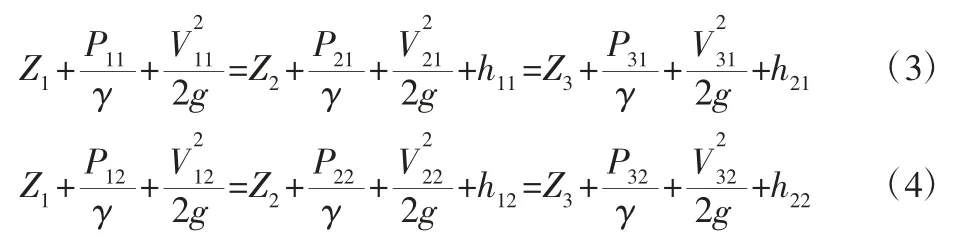
式中:V—质点流速;
P—质点压强;
γ—质点容重;
Z—节流件位置势能;
h—水头损失。
通过式(3)、式(4)可知,影响流量计测量准确度的主要是水头损失,而水头损失包括沿程水头损失hλ和局部水头损失hζ[5],外流道和内流道的沿程损失分别为:

式中:ρ—流体密度;L—流体经过的路程;R、r—内外流道水力半径;Qv1、Qv2—流量;μ—动力粘度系数。
外流道和内流道的局部水头损失为:
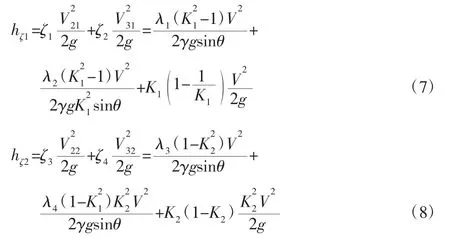
式中:V—质点流速;
ζ—局部阻力系数;
λ—沿程阻力系数;
θ—扩散角;
k—与前后扩散角有关的系数;
K—流道的压缩比。
从推导出的与沿程水头损失和局部水头损失相关的结构参数为异径比、扩散角和节流件的大径。这三个参数对节流件的性能影响最大,故选择这三个参数为优化的目标。
3 试验设计和流场仿真
3.1 试验设计
根据分析,影响压损差的主要参数异径比k、扩散角θ 和节流件的大径R。根据以往的研究确定三个控制参数的变化范围:异径比k为(0.5~0.9);扩散角 θ 为(4~10)°;节流件的大管半径R为(5~9)mm。采用二次回归正交试验的设计方法,利用二次正交回归表设计15 组不同的试验模型[6]。试验模型设计,如表1 所示。

表1 各试验模型结构参数Tab.1 Structural Parameters of Each Test Model
3.2 流场仿真
利用三维软件对15 组试验进行建模,而后流场仿真采用ANSYS 的FLUENT 模块进行仿真,采用非结构四面体网格划分,按照网格划分的原则,参数变量的变化大区域要细化网格以提高精度,梯度小的区域网格稀疏以节省计算资源。具体到这里的网格划分中,在节流件前后的流场网格稀疏,在节流件周围的网格划分尽量细化[7],网格划分,如图2 所示。

图2 半剖流场网格划分Fig.2 Half-Section Flow Field Meshing
在湍流模型的选择上,双向内外管压差流量计的节流件采用对称结构,流体虽然被分为内外两个流道,但在节流件中部有一段稳定流态的直管段,当流体流过节流件后,内外流道流体的流速和压力逐渐恢复一致,在流场中并没有太大的压力梯度。RNGk-ε 模型来源于严格的统计技术,相较于标准k-ε 模型改善了精度,而且考虑到了湍流漩涡,在这方面的精度也较高。综合考虑,湍流模型采用RNGk-ε 模型作为仿真模型。
仿真介质选择液态水,温度20℃,不可压缩流体,管道直径为DN32PVC 管道的内径27.2mm,出口条件为outflow。求解方法选择比较适合解决问题的SIMPLE(半隐式连接压力方程)。在FLUENT 的后处理中,创造一个截面以方便观察截面上的压力分布和方便设置取压点。取压需要在流场稳定的时候取,故计算压损的前后取压点设置在节流件的前后一个管道直径的距离,计算压差信号的两个取压点设置在节流件中心和外流道中心。
4 仿真结果和数据分析
每组试验进行仿真,对四个取压点的相对压强进行记录,并计算出前后测点的压差,内外测点的压差,传统评价指标压损比为内外压差信号与前后压损的比值[8],用压损比作为评价指标的初衷是为了选出内外压差尽可能大而前后压损尽可能小的结构参数[9],但是避免不了内外压差与前后压损同样都很小但是它们比值却很大的情况。所以压损比这一评价指标有一定的漏洞。而压损差为内外压差信号与前后压损之差,这一指标相比于压损比,更加的科学合理。在流速1m/s 的入口流速下,其中,一组的试验压力云图,如图3 所示。所测得的数据,如表2 所示。
根据表3 的数据,在保证每一项的回归系数的可信度至少大于75%的前提下,可以拟合出二次回归方程:
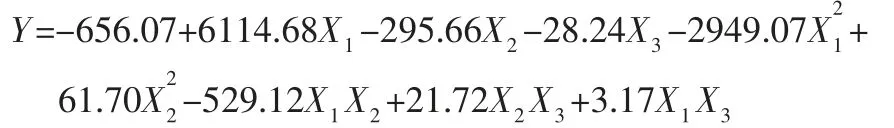
式中:Y—压损差;X1、X2、X3—异径比、扩散角和节流件大管半径三个结构参数。

图3 仿真结果压力云图Fig.3 Simulation Results Pressure Cloud Map

表2 流速1m/s 下各组试验数据Tab.2 Test Data of Each Group at a Flow Rate of 1m/s
利用同样的方法,分别在入口流速为1.5m/s、2m/s、2.5m/s 的条件下进行仿真。得到的,流速1.5m/s 入口流速下,拟合出的方程为:
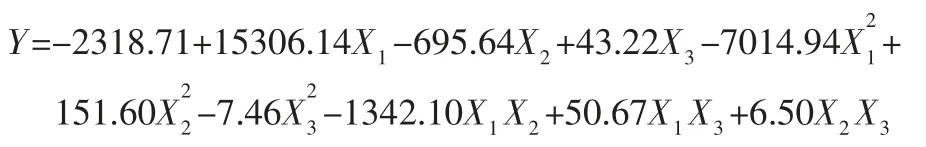
流速2m/s 入口流速下,拟合出的方程为:
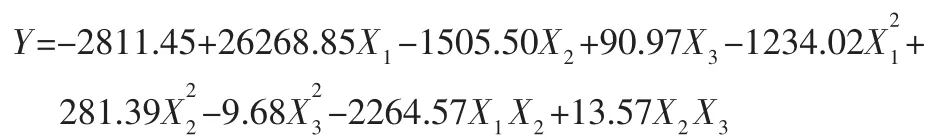
流速2.5m/s 入口流速下,拟合出的方程为:
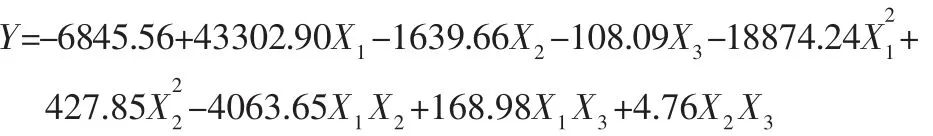
利用Matlab 优化工具箱中的fmincon 函数对上述模型进行寻优计算[10],对入口流速1m/s 条件下拟合出的方程进行寻优,具体程序如下:


同样的程序分别对其余函数进行寻优,寻找出的最优解结果相差很小。为了方便建模对参数取整,得到的最优结构参数为异径比0.5、扩散角9°和节流件的大管半径9mm。根据最优参数进行建模,在FLUENT 中同样的边界条件下仿真,记录参数,并与回归方程的理论最大值进行对比。对比结果,如表3 所示。

表3 理论最大压损差与实际压损差对比Tab.3 Comparison of Theoretical Maximum Pressure Loss Difference and Actual Pressure Loss Difference
随着入口流速的增大,压损差的值也随之增大。各流速条件下实际压损差与理论最大压损差的偏差不超过8%,如表3 所示。对最优模型的仿真与15 组试验所测得的数据相比,最优模型压损差高于所有的试验,如图4 所示。
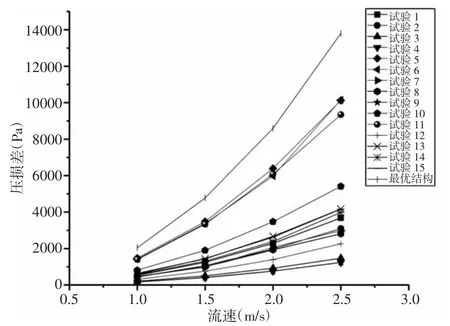
图4 压损差对比折线图Fig.4 Pressure Loss Difference Comparison Line Chart
5 结论
(1)在分析了以往内外管压差流量计的评价指标压损比的漏洞所在,提出对双向内外管压差流量计的新的评价指标压损差。压损差相对于压损比,避免了压差信号与前后压损同时很小,压差信号不能满足实际需求这样的情况,更加科学合理。
(2)通过对双向内外管压差流量计模型结构和计算原理的分析,寻找出影响流量计性能的主要结构参数为异径比k、扩散角θ 和节流件的大径R。
(3)根据二次回归正交试验的设计方法,设计出15 组试验,并利用 FLUENT 分别在入口流速 1m/s、1.5m/s、2m/s、2.5m/s 的入口流速下,对各组试验进行了仿真,通过记录的数据拟合出二次回归方程,利用Matlab 优化工具箱中的fmincon 函数对得到的方程进行寻优计算,最终确定优结构参数为异径比0.5、扩散角9°和节流件的大管半径9mm。
(4)通过验证,寻找的最优结构节流件的性能优于所有的试验组合,并且理论与实际的压损差的误差不超过8%。与以往的流量计相比,压差信号更大,前后压损更小,测量更加准确,对流体扰动更小的效果,能够适应更多的工业场合。

