基于PSR-MDS模型的水资源承载力评价研究——以河北省为例

王 晶，耿 燕，郑 雪

(1.燕山大学 经济管理学院，河北 秦皇岛 066004； 2.燕山大学 区域经济发展研究中心，河北 秦皇岛 066004； 3.燕山大学 理学院，河北 秦皇岛 066004； 4.河北省秦皇岛水文水资源勘测局，河北 秦皇岛 066004)

1 研究背景

水是人类生存和经济发展必不可少的宝贵资源。随着我国经济的快速发展，人口的增长与社会经济的繁荣对水资源的开发利用提出了更高的要求。一直以来，反映水资源利用程度的水资源承载力的研究备受关注。水资源承载力是指某一地区的地表和地下水资源在保证正常的社会物质生活水平下，供给工农业生产、生态环境保护等用水的最大能力，以及水资源所能持续供养的人口数量[1]。

目前，对水资源承载力的研究主要集中在水资源承载力评价指标体系的构建与指标权重的确定2个方面。在构建水资源承载力评价体系上，主要有两大研究方向，一个是在经典模型上进行改进，另一个是提出新的研究模型。

在改进经典模型方面，张天宇等将层次分析法运用到模糊综合评价模型，在模型中合理地加入了主观因素[2]；左其亭等在TOPSIS模型上增加了预评分来计算水资源承载力的最后得分，以最大程度地排除个别不合理数据的干扰[3]；许杨等利用DPSR改进的TOPSIS模型，较好地反映了数据序列之间的非线性关系[4]；望开发等通过均值化取代标准化的改进主成分法，避免了算法的差异性和局限性[5]；张彦来等引入主分量分析法，对可变模糊算法进行了改进[6]。

在新模型方面，白露等运用Logistic 关联分析把定性分析与定量分析相结合，不仅从整体上描述了区域水资源承载力的水平，而且还保证了评价结果的可靠性[7]；刘童等利用集对分析方法建立的五元联系数模型全面而完整[8]；韩刚建立的COIM模型，提高了承载力计算的精确度[9]；王大本等利用WSR方法论，对水资源承载力进行了全面综合评价[10]等。

在确定指标权重方面，王大本等利用熵值法及系统耦合法对26个评价指标进行了赋权，并考虑了系统内部因素之间的关系[10]；董会忠等将变权理论运用到水资源承载力的评价中，可以更合理地研究所选取指标的不均衡性，同时也使研究结果更加接近区域实际[11]；安强等采用层次分析法和熵权法相结合的综合赋权法来确定指标权重，从而克服了层次分析法主观性强以及熵权法过分依赖于指标变化率的缺陷[12]。

结合前人的研究成果，本研究建立了更为全面客观的PSR-MDS水资源承载力评价模型。如图1所示，模型主要分为三大部分，首先是从水资源承载压力(P)、支撑力(S)、调控力(R)三大方面来确定水资源承载力的评价指标；然后利用粒子群算法寻找最优的组合系数，将因子分析法与熵值法确定的指标权重进行综合，由此建立PSR模型；同时为了克服人为划分等级的主观性，利用相似度结构分析法(MDS)对综合评分进行相似度评价。

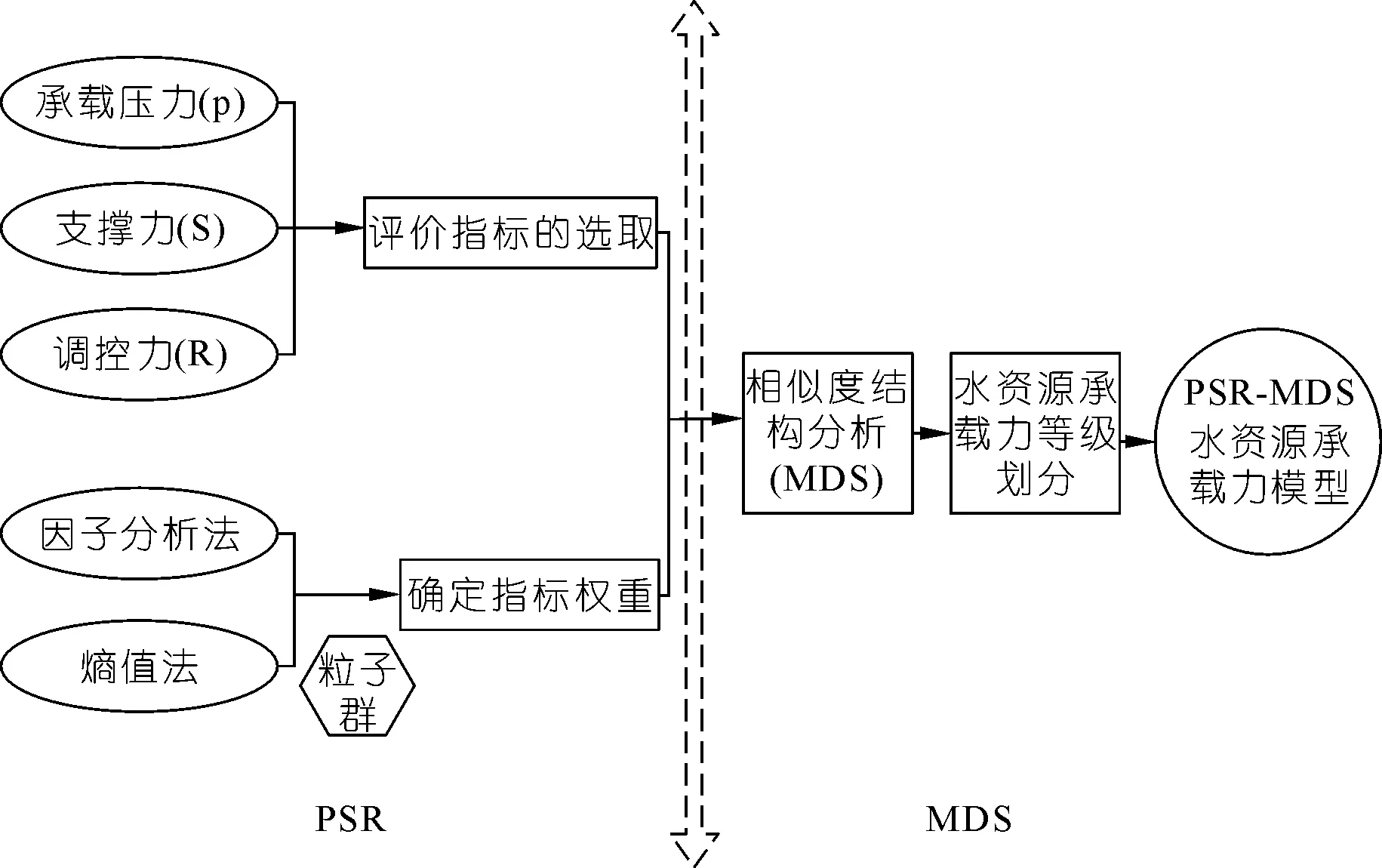
图1 PSR-MDS水资源承载力评价模型Fig.1 PSR-MDS water resource bearing capacity evaluation model

2 水资源承载力评价指标设计

水资源承载力受多方面要素的影响，为了保证评价体系的完整性和全面性，本研究从水资源承载压力、支撑力以及调控力三大方面分别综合考虑到了经济、生态、社会发展变化等要素，从而建立了PSR模型。在选取具体指标时主要遵循如下原则：① 能够反映水资源承载力问题的本质；② 对水资源承载力变化较敏感；③ 减少重复性指标。

在PSR模型中：① 承载压力(P)指人类活动对水资源承载负荷产生的影响，故将与用水密切相关的人类活动作为评定承载压力的指标，包括人口密度、用水定额、万元工业增加值用水量、万元GDP用水量；同时，考虑到城市的人口密度和发展水平在很大程度上影响了水资源的开发利用情况，故将城镇化率也选取为评价指标。② 承载支撑力(S)代表水资源环境压力下所呈现出的水资源现状水平，主要指水资源数量支撑力，包括人均水资源可利用量、年产水模数以及年供水模数，考虑到森林的面积可对降水量产生较大的影响[13]，从而对水资源数量会产生影响，故将森林覆盖率也作为评价指标。③ 承载调控力(R)指水资源环境与人类活动之间的转换与联系，其中包括水资源开发利用率、生态用水率，由于水资源是一切社会活动的基础，肯定也会对经济造成一定的影响，同时经济在一定程度上也会对水资源的开发、利用造成影响[14]，故选取能够反映经济情况的人均GDP作为评价指标。

据此，本研究建立的PSR模型最终形成了“5+4+3”的“三层、三维”评价体系，如图2所示。由图2可以看出：模型能够较系统地表明经济社会发展对水资源状况承载安全造成的变化与影响，可以反映水资源与经济社会的相互影响关系。水资源承载压力可逆向地反映水资源支撑力，水资源支撑力能正向影响承载的调控力；同时，调控力在一定程度上又决定了承载压力的大小。三大因素互相影响，彼此制约，形成水资源承载系统动态影响与评估体系。

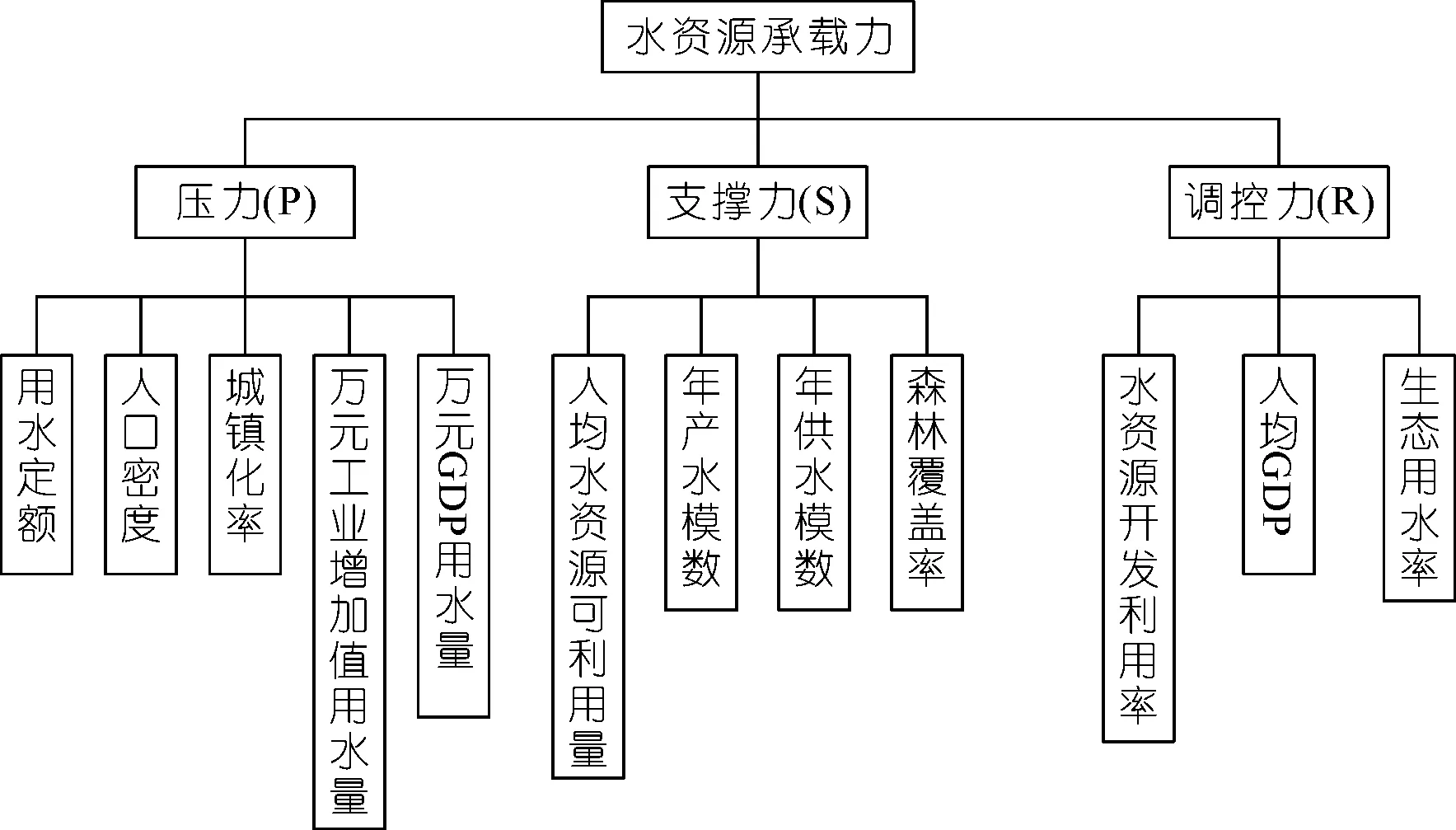
图2 评价指标选取Fig.2 Selection of evaluation indices

3 综合指标权重寻优

因子分析法是一种指标与指标之间的权重确定方法，通过探讨各指标之间相互影响或联系来确定指标的权重；熵值法是一种指标自身权重确定的方法，通过计算各指标所含信息的有序程度和反映样本数据变化速率的信息熵来确定权重。这2种方法分别从不同指标间的关系和指标本身的相关信息2个方面来确定权重，因此，如果将2种方法组合在一起，便能更加全面客观地确定指标权重。为了保证2种方法的组合系数合理、准确，本研究根据离差平方和最小原则[15]，采用粒子群算法来寻找最优的因子分析法权重系数和熵值法权重系数，使得这2种方法在加权之后的指标权重离差平方和最小。具体步骤描述如下。

Step 1：数据标准化。取n个城市，每个城市有p个指标，得到原始矩阵X=(xij0)n×p，对数据进行标准化，消除量纲影响：

(1)

式中：xij0为第i个城市第j个指标的原始数据；min(xij0)为第j个指标的最小值；max(xij0)为第j个指标的最大值；xij为标准化后的指标数据。

Step 2：确定因子分析法权重。取因子分析的累积贡献率大于80%的前m个主因子，求权重系数βj=A1jf1+A2jf2+…+Amjfm，其中,fi是主因子Fi的贡献率，Aij是第i个主因子对第j个变量的得分值，即特征值所占百分比。由此得到第j项指标的权重如下：

(2)

Step 3：确定熵值法权重。首先计算指标信息熵值e，第j项指标信息熵值计算公式如下：

(3)

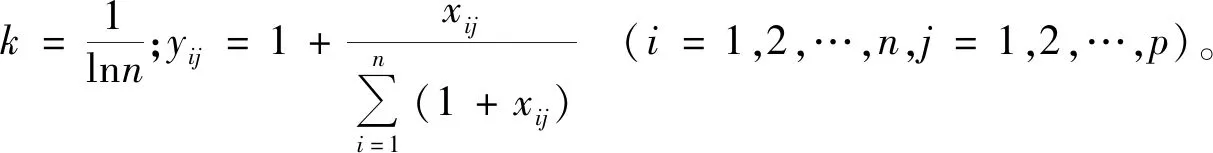
其次，计算评价指标的熵权，运用熵值法来确定各指标的权重，其本质是利用信息熵来计算，第j项指标的权重为

(4)

Step 4：基于粒子群算法优化综合权重。根据离差平方和最小原则，寻找最优的因子分析法权重系数a和熵值法权重系数b，使得2种方法加权之后的权重系数离差平方和最小。这样得到的综合权重rj可在一定程度上弥补2种赋权方法的不足。

(5)

rj=awj+bqj

(6)

具体步骤如下：

(1) 因为权重系数a和b是相对的，则可假设a=1，则初始粒子位置为μ0=(w1，w2，…，wp)。

(7)

(8)

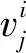
(3) 更新粒子i位置

μi=μi+τvi

(9)

式中：τ为约束因子，控制速度的权重。

(4) 在当前群中，比较每个粒子的适应度函数值是否比历史局部最优值好，从中选取最佳的适应值对应的粒子位置作为全局最优值所在位置。

(5) 重复步骤(2)～(4)，直至前后最优位置的适应值之差小于设定值ε。

Step 5：计算得分。根据所得到的综合权重rj来计算每个城市的水资源承载力得分情况si，即

(10)

4 水资源承载力等级划分

相似度结构分析是将多维空间的变量简化到低维空间，同时又保留原始对变量间关系的一种数据定位、分析和归类的降维方法，也是数据可视化的一种手段。将PSR模型中的指标形象化地映射到二维空间中，根据分类情况来划分水资源承载力的等级。具体步骤描述如下：

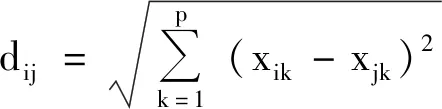
(11)

5 河北省水资源承载力评价

5.1 研究区域概况

以河北省作为本文实例研究区。河北省地处东经113°27′～119°51′，北纬36°05′～42°40′之间，地理位置非常重要，有京广、京九、京沈、京包等重要铁路线经过。其地域辽阔，自然资源丰富，日照充足，是全国粮、棉、油的高产地。河北省的水资源主要由地表水、降水、地下水供给，拥有19座大型水库及45座中型水库，共蓄水40亿m3左右。河北省总供水量为182亿m3左右，而需水总量却在248亿m3左右。河北省人口密度大，承担着保护北京用水安全、保护水生态环境等重要使命。在现状供用水条件下，即使充分考虑节水改造、新建水源等措施，河北省水资源供需形势仍较为严峻。

5.2 数据来源

考虑到各项指标数据选取时间的一致性，本文对河北省各城市水资源承载力评价的时间段选为2018年。相应数据来源为《河北省水利厅水资源公报》《秦皇岛市2018年国民经济和社会发展统计公报》《廊坊市2018年国民经济和社会发展统计公报》《邯郸市2018年国民经济和社会发展统计公报》《邢台市2018年国民经济和社会发展统计公报》《石家庄市2018年国民经济和社会发展统计公报》《2018保定经济统计年鉴》《衡水市2018年国民经济和社会发展统计公报》《沧州市2018年国民经济和社会发展统计公报》《唐山劳动日报》《张家口市2018年国民经济和社会发展统计公报》，以及《承德市2018年国民经济和社会发展统计公报》。2018年，全省地表水资源量为85.32亿m3，地下水资源量为124.41亿m3，扣除地表水和地下水资源的重复计算量，全省水资源总量为164.04亿m3，人均及亩均水资源量分别为217.09 m3和167.70 m3。根据2018年河北省代表站年降水量分析计算结果，2018年全省平均降水量为507.60 mm，比多年平均值少24.10 mm，属平水年份。

5.3 结果分析

5.3.1指标权重

根据文中所述方法得到的因子分析法与熵值法的最佳权重系数分别为1.000和1.433，各评价指标及其权重如表1所列。根据表1数据，水资源承载力的大小与城镇化率、产水模数、供水模数、人均GDP大小成正比，与用水定额、人口密度、万元工业增加值用水量、万元GDP用水量、人均资源可利用量、森林覆盖率、水资源开发利用率以及生态用水率成反比。其中，人口密度、万元工业增加值用水量、水资源开发利用率，以及人均GDP在评价体系中占有重要地位。

此外，由表1的3种方法得到的指标权重结果不难看出：单纯因子分析法确定的权重中，年产水模数指标从主观理解上是正作用于水资源承载力水平的，但其权重却为负数；单纯熵值法确定的权重中，所有指标的权重均为同号，这也存在一定的不合理性。因此，综合权重法确定的指标权重更符合实际。

5.3.2城市得分情况

(1) 承载压力(P)方面。根据公式(10)，取评价指标q1～q5，即j取1～5，计算各城市在水资源承载压力方面的得分，得到的结果如图3所示。由图3可知：邯郸市和邢台市承载压力较小，而承德市和秦皇岛市承载压力较大。

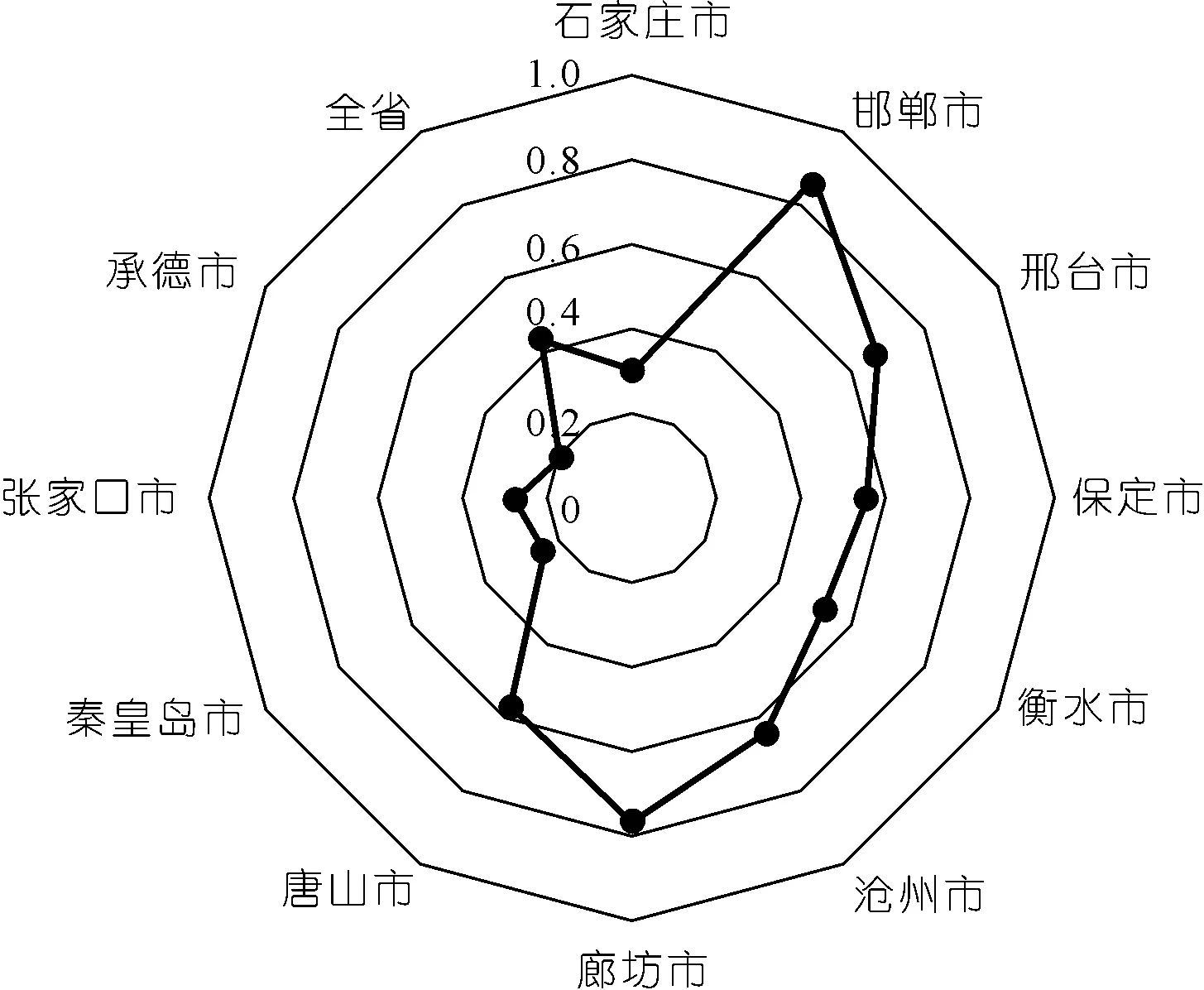
图3 河北省各城市水资源承载压力得分Fig.3 Water resources bearing pressure score (pressure) of each city in Hebei Province

(2) 承载支撑力(S)方面。根据公式(10)，取评价指标q6～q9，即j取6～9，得到各城市在水资源承载支撑力方面的得分结果(见图4)。由图4可知：邢台市和承德市具有较丰富的水资源，相比之下，石家庄市的水资源更显短缺之势。

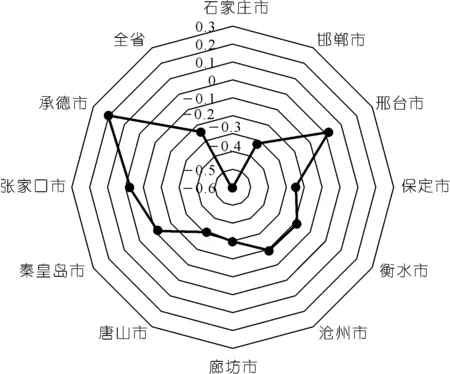
图4 河北省各城市水资源承载支撑力得分Fig.4 Scores of water resources carrying capacity(support) of each city in Hebei Province

(3) 承载调控力(R)方面。根据公式(10)，取评价指标q10～q12，即j取10～12，得到各城市在水资源承载支撑力方面的得分结果(见图5)。由图5可知：石家庄市和唐山市水资源与人类活动之间的转换均衡，而邢台市和保定市的转换有待加强。

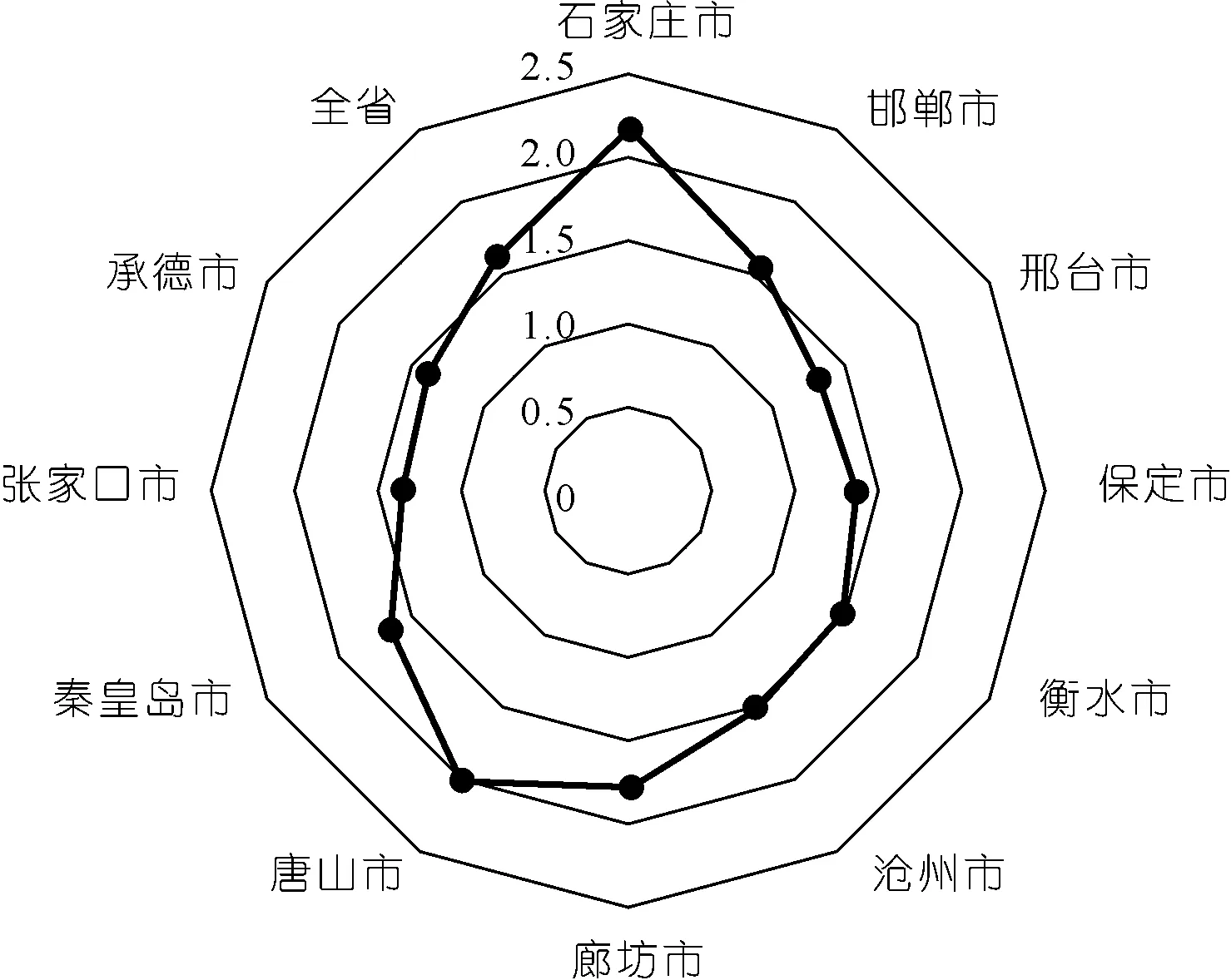
图5 河北省各城市水资源承载调控力得分Fig.5 Scores of water resources carrying capacity regulation of each city in Hebei Province

综合12个评价指标，公式(10) 中取q=12，得到了各城市水资源承载力综合得分情况(见图6)。由图6可知：唐山市、承德市和秦皇岛市的水资源综合承载力居河北省前三位，而衡水市、邯郸市和家庄市的承载力较弱。

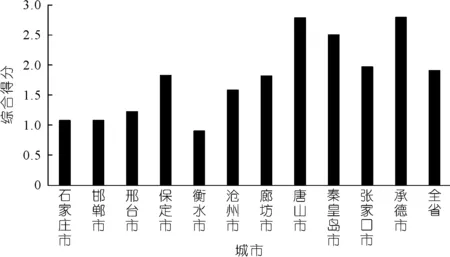
图6 河北省各城市综合得分Fig.6 Comprehensive scores of each city in Hebei Province

5.3.3城市等级划分

运用SPSS，对各城市的综合得分进行相似度结构分析，根据度量结果(见图7)。很明显地，将河北省水资源承载力情况分为3个等级：① 一级为唐山市、承德市、秦皇岛市；② 二级为张家口市、保定市、廊坊市、沧州市；③ 三级为石家庄市、邢台市、邯郸市、衡水市。河北省的水资源承载力平均水平处于第二等级。在一级水平城市中，以唐山市为例，其较高的水资源承载力离不开较高的人均GDP，较低的人口密度、万元工业增加值用水量、水资源开发利用率。而在三级城市中，以石家庄为例，虽然石家庄市的人均GDP处于较高水平，但其人口密度、万元工业增加值用水量、水资源开发利用率都是全河北省最高的城市，这是其水资源承载力水平并不高的直接原因。

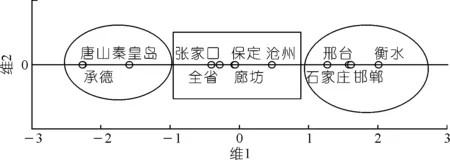
图7 城市等级划分结果Fig.7 Results of city grade classification

6 结 论

(1) 本文建立的PSR-MDS模型，能够比较客观地确定指标权重，并能根据综合得分相似度来确定承载力的等级，这样不仅能全面细致地描述地区水资源承载力的水平，而且能最大程度地降低人为客观因素，保证了评价结果的可靠性。

(2) 河北省的数据分析表明：在水资源承载力评价中影响较大的评价指标包括人口密度、万元工业增加值用水量、水资源开发利用率，以及人均GDP。

(3) 河北省各市在水资源承载压力、水资源承载支撑力以及水资源承载调控力等方面存在着一定的差异，各市应根据其实际情况进行水资源调配及合理使用，以保证经济发展的可持续性，提高水资源承载力水平。