电机弹性架悬高速转向架蛇行频率跳变现象分析

黄彩虹，宋春元,，范 军，曾 京

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.中车长春轨道客车股份有限公司，吉林 长春 130062)

由于动车组动力分散，牵引电机被分散地安装于各个动车转向架。根据列车运行速度对不同牵引功率的要求，电机质量从几百千克到一吨不等。研发更高速度等级的高速列车还将进一步增加牵引电机质量，而簧间质量的增加会降低转向架的蛇行运动稳定性。通过板簧、橡胶节点或者吊杆将牵引电机整体悬挂于转向架构架(图1)，可明显改善转向架高速运行时的蛇行运动稳定性，因此高速列车普遍采用此种安装方式[1-2]，我国CRH3、CRH380B/C/D、CR400BF型动车组牵引电机就是采用的这种悬挂方式。

图1 某高速列车牵引电机架悬结构

国内外学者对电机弹性架悬转向架的动力学性能进行了广泛的研究。文献[3-7]在机车牵引电机弹性架悬动力学理论和转向架结构方案设计等工程应用方面进行了诸多探索，分析其中的动力吸振现象，并研究电机吊杆位置和长度对横向动力学性能的影响。文献[8]分析电机悬挂频率和阻尼比对高速列车临界速度的影响，通过根轨迹分析和时域仿真解释电机弹性架悬的动力吸振原理。文献[9-12]研究高速列车转向架电机弹性架悬参数对稳定性的影响，指出存在一个最佳的电机悬挂频率，当电机悬挂频率低于该最佳值时，转向架可以获得较高的蛇行运动稳定性，并且还探讨了悬挂参数和轮轨参数对最佳悬挂频率的影响。

在线路试验研究方面，针对电机弹性架悬转向架动力学性能进行了长期跟踪测试。被试对象为某350 km/h高速动车组动车转向架和拖车转向架，所有运行状态均一致，车轮踏面磨耗状态也一致。图2给出了京沪线常州北—上海虹桥站间，运行速度350 km/h时动/拖车转向架在一个镟轮周期内蛇行频率的演变规律。其计算方法如下：采集得到动/拖车构架端部横向加速度，以6 s为时长进行FFT计算，一个站间所有6 s频谱的平均值即为一天的平均频谱，将测试获得所有的平均频谱进行累积，即可获得不同里程下的蛇行频率演变规律。可见，在一个镟轮周期内，拖车转向架蛇行频率从5 Hz逐渐增加到8 Hz，呈线性增加趋势。动车转向架(电机弹性架悬)在0～15万km范围内蛇行频率从4 Hz逐渐增加到6 Hz，15万km后蛇行频率随着运行里程的增加存在跳变现象(4～6 Hz跳变到8～9 Hz)。从图3给出的动车转向架在整个京沪线的构架横向加速度时频图可以看出，动车转向架蛇行频率跳变仅发生在常州北—上海虹桥的局部路段，且随运行里程增加愈发显著。巧合的是，多个动车组在该路段出现了构架横向加速度报警和车体抖动现象。通过现场钢轨廓形测试发现该路段钢轨轨顶扁平，轨角突出，导致轮轨匹配等效锥度较其他路段偏大。镟轮后运行13万、15.2万、18.1万、24.6万km实测车轮踏面与该路段钢轨廓形匹配后的等效锥度分别为0.25、0.31、0.34、0.40，而与标准60 kg/m钢轨廓形匹配的等效锥度均小于0.28，如果考虑与设计打磨廓形60N匹配其等效锥度更低。综上所述，频率跳变发生在15万km左右，此时频率跳变路段的实际轮轨匹配等效锥度为0.31。从后文的理论分析可以看出，轮轨匹配等效锥度增大是引起蛇行频率跳变的外因，而动车转向架特殊的电机架悬参数是引起频率跳变的内在因素。如果延长列车镟轮周期，更多路段的轮轨匹配等效锥度将达到跳变条件。

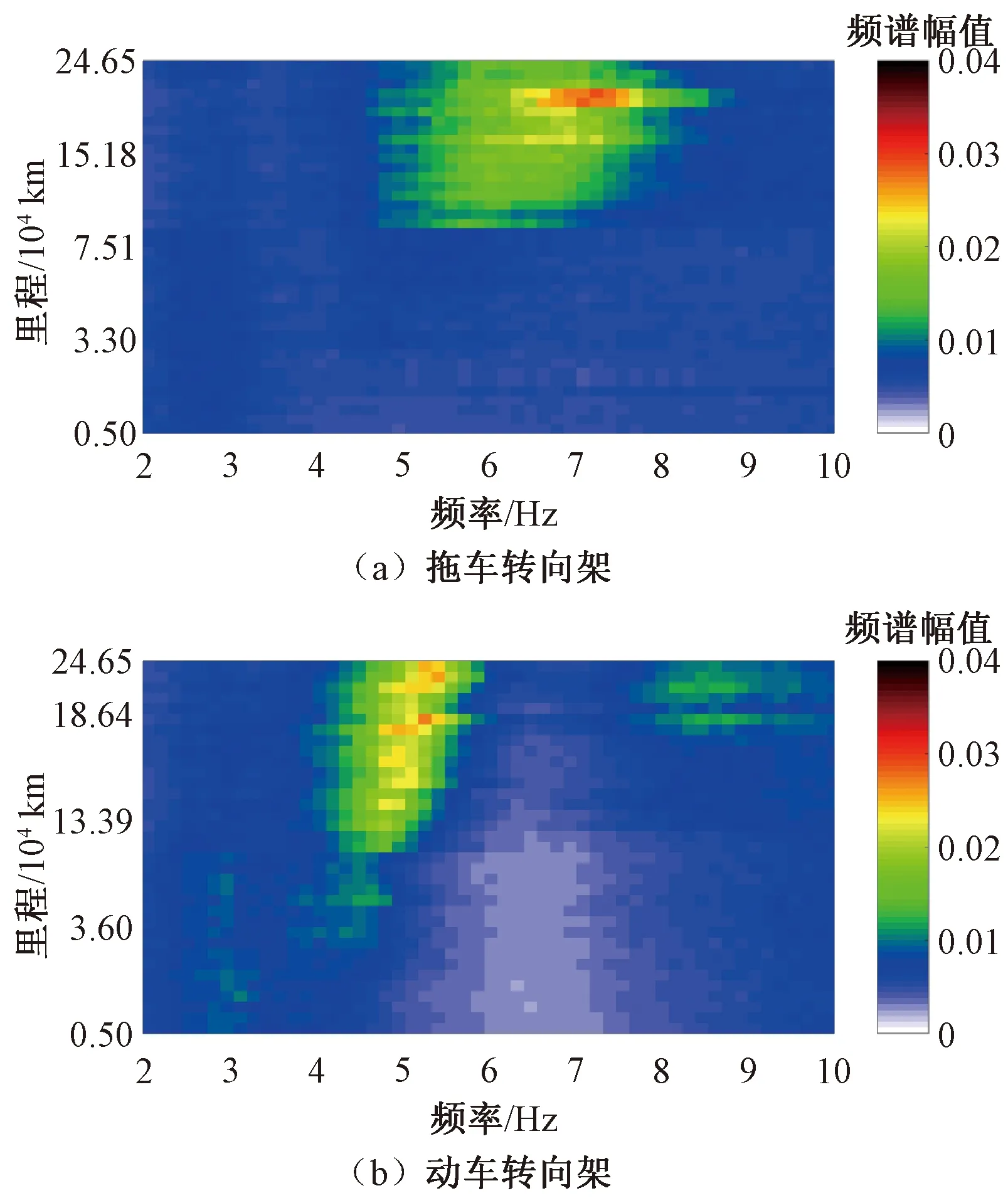
图2 常州北—上海虹桥站间某高速动车组蛇行频率随运行里程的演变

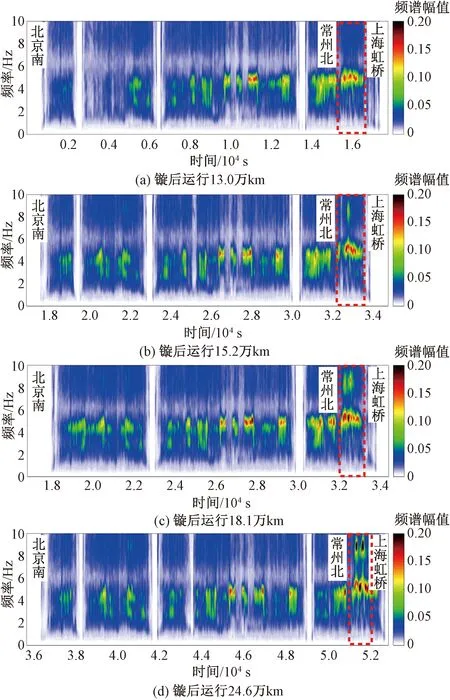
图3 京沪线某高速动车组构架横向加速度时频图

为了解释转向架蛇行频率的跳变现象，在前期研究基础上建立电机弹性架悬转向架横向动力学模型，研究等效锥度变化对蛇行频率的影响，发现蛇行频率存在跳变特征，通过系统特征值根轨迹分析对该现象进行理论解释，并利用时域仿真手段进行验证。最后分析电机架悬参数对蛇行频率跳变特征的影响，揭示蛇行频率跳变的存在条件。研究成果可为电机弹性架悬参数设计和实际线路运行中蛇行频率跳变现象的解释提供理论依据。

1 电机弹性架悬转向架横向动力学模型

转向架蛇行运动稳定性属于横向动力学问题，与垂向自由度基本没有关系，所以在进行动力学建模时仅考虑轮对、构架以及牵引电机的横向和摇头自由度，如图4所示。其中，一系悬挂连接轮对和构架，二系悬挂连接构架和车体，电机悬挂连接电机和构架。由于本文主要关注转向架的蛇行运动稳定性，车体自由度可不作考虑，仅仅作为一个参考系沿着轨道方向以恒定的速度运行。为了研究的方便，在进行动力学建模时做出以下假设：

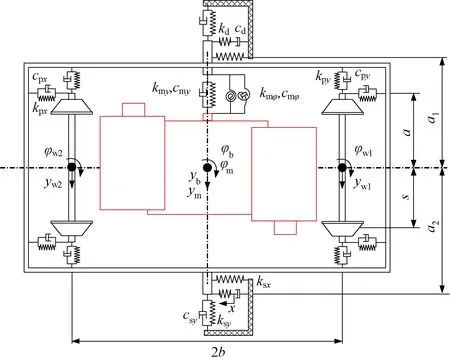
图4 电机弹性架悬转向架模型

(1)结构对称。

(2)构架质心高度和车轴中心线一致，由此可以忽略构架侧滚自由度的影响。

(3)轮轨蠕滑力和悬挂作用力工作在线性区。

(4)忽略重力刚度和自旋蠕滑的影响。

假设轮对的横移和摇头自由度为yw1、yw2、φw1和φw2，构架的横移和摇头自由度为yb和φb，电机的横移和摇头自由度为ym和φm，抗蛇行减振器串联模型的中间自由度为x，电机弹性架悬转向架系统动力学方程可以表示为

2kpyyw1-2f22φw1-2kpyyb-2bkpyφb=0

( 1 )

( 2 )

2kpyyw2-2f22φw2-2kpyyb+2bkpyφb=0

( 3 )

( 4 )

2kpyyw1-2kpyyw2+4kpyyb+2ksyyb+

( 5 )

2a2kpxφw1+2bkpyyw2-2a2kpxφw2+(4b2kpy+

4a2kpx)φb+2ksxa12φb+ 2kda2(φba2-x) +

( 6 )

( 7 )

( 8 )

( 9 )

式中：a为一系悬挂横向跨距之半；s为名义滚动圆跨距之半；a1为二系悬挂横向跨距之半；a2为抗蛇行减振器横向跨距之半；Mb和Ib为构架质量和转动惯量；Mw和Iw为轮对质量和转动惯量；Mm和Im为电机质量和转动惯量；kpx和cpx为一系纵向刚度和阻尼；kpy和cpy为一系横向刚度和阻尼；ksx为二系纵向刚度；ksy和csy为二系横向刚度和阻尼；kmy和cmy为电机悬挂总的横向刚度和阻尼；kmφ和cmφ为电机悬挂总的摇头刚度和阻尼；kd和cd为抗蛇行减振器的串联刚度和串联阻尼；λ、r0、f11和f22分别为等效锥度、滚动圆半径、纵向蠕滑系数和横向蠕滑系数。

为了得出一般性结论，用电机悬挂的横移频率fmy和横移阻尼比ζmy代替电机悬挂总的横向刚度kmy和总的横向阻尼cmy。同理，可用电机悬挂的摇头频率fmφ和摇头阻尼比ζmφ代替电机悬挂总的摇头刚度kmφ和总的摇头阻尼cmφ。其关系式可以表示为

(10)

(11)

此外，还建立了不考虑电机自由度的转向架模型(记为无电机模型)以及电机刚性固结的转向架模型(记为电机固结模型)。以上参数取值见表1。

表1 动力学模型参数及取值

2 转向架蛇行频率的跳变现象

假设转向架系统线性化方程为dx/dt=Ax，方程的解可以表示为x(t)=ψeσt，其中特征值σ以及特征向量ψ由方程(A-σI)ψ=0定义[13]。特征向量ψ代表各模态的振型，特征值σ的实部表示各模态的阻尼值，虚部表示各模态的频率。将特征值σ的实部和虚部进行一定的变换，可以得到各模态的振动频率f和阻尼比χ，f= Im(σ)/(2π)(单位Hz)，χ= Re(σ)/|σ|(无量纲)。阻尼比小于0时系统稳定，阻尼比大于0时系统失去稳定。

图5给出了运行速度为350 km/h、等效锥度从0.1变化到0.6时系统特征值根轨迹曲线，等效锥度间隔为0.01，等效锥度越大根轨迹的尺寸也越大。这里只给出了低频范围内，与蛇行运动有关的两个主要模态(转向架蛇行和电机横移)的根轨迹曲线。从图5可以看出，存在A和B两个与等效锥度变化相关的根轨迹曲线。等效锥度较低时，根轨迹曲线A的阻尼比更靠近0，转向架主要体现A的振型(3～5 Hz)。等效锥度较高时，根轨迹曲线B的阻尼比更靠近0，转向架主要体现B的振型(7～9 Hz)。存在一个临界等效锥度(在0.35附近)，当等效锥度小于该临界值时主要体现A的振型，大于该临界值时主要体现B的振型。由于根轨迹曲线B的振动频率远大于根轨迹曲线A的振动频率，因此在同一运行速度下，随着等效锥度的增加，转向架振动频率将从3～5 Hz跳变到7～9 Hz。

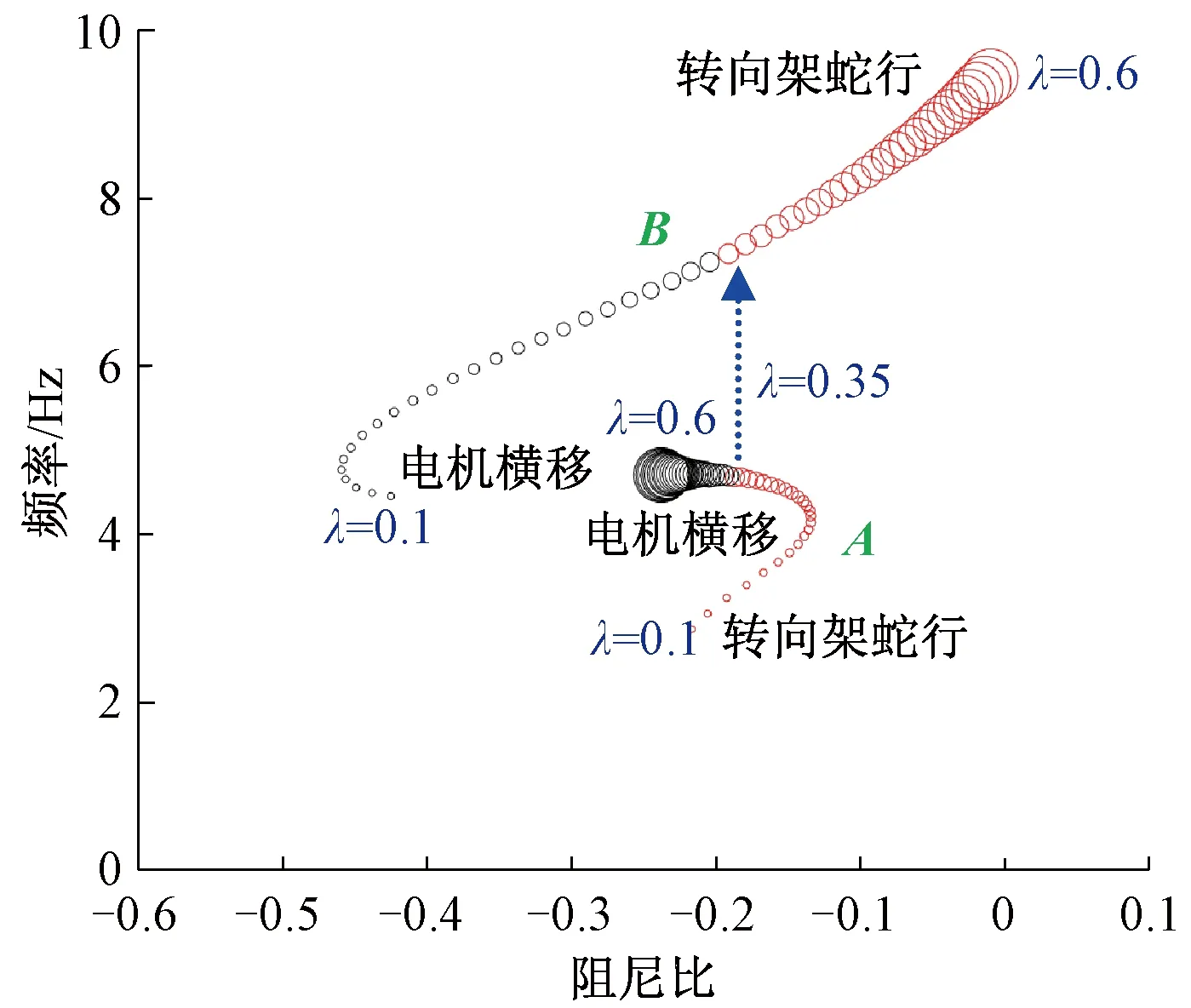
图5 特征值随等效锥度的变化曲线

为了解释其中的原因，图6给出了不同运行速度下系统特征值根轨迹曲线。车辆运行速度从5 km/h变化到350 km/h，间隔为5 km/h，运行速度越大根轨迹的尺寸也越大，图案由空心变为实心时，表示遇到50 km/h的整数倍速度，即50，100，…，350 km/h。结合图6并分析图5中各特征值的振型可以看出：当等效锥度取0.1时，图5中根轨迹A代表电机横移和转向架同向的蛇行运动，而根轨迹B代表电机横移模态。当等效锥度取0.6时，根轨迹A代表电机横移模态，而根轨迹B代表电机横移和转向架反向的蛇行运动。根轨迹A和B的振型在等效锥度0.1～0.6之间发生了反转。从图7的频率轨迹演变趋势可以看出，这是由于在等效锥度增加过程中电机横移和转向架蛇行两个模态的频率轨迹发生了从不相交到偏转再到相交的演变。该演变并非跳跃式的，而是一个逐渐的过程。特征值根轨迹偏转[14-15]指两条根轨迹曲线看上去即将相交，它们彼此靠得越来越近，但随着参数变化突然偏转方向，分别朝着另一条曲线先前的方向继续前进。两个特征向量在特征值曲线偏转之后并没有沿着所属的特征值保持原方向前进，而是跑到了各自对方的路线上，即特征值曲线发生偏转后，其中一条曲线对应的特征向量与另一曲线先前所对应的特征向量一致。关于特征值曲线偏转的问题，国内外学者已有过一些探讨，如杆的振动、旋翼振动、圆盘振动及柱的弯曲振动等。

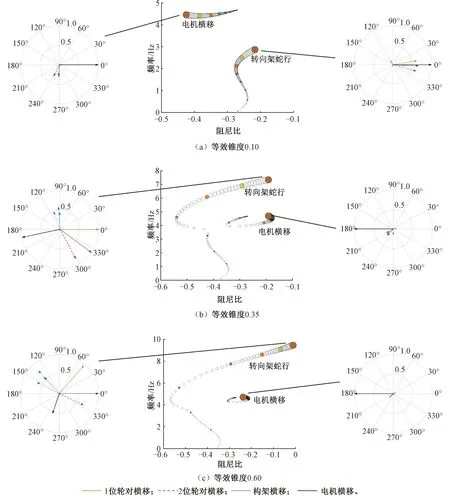
图6 特征值随运行速度的变化曲线

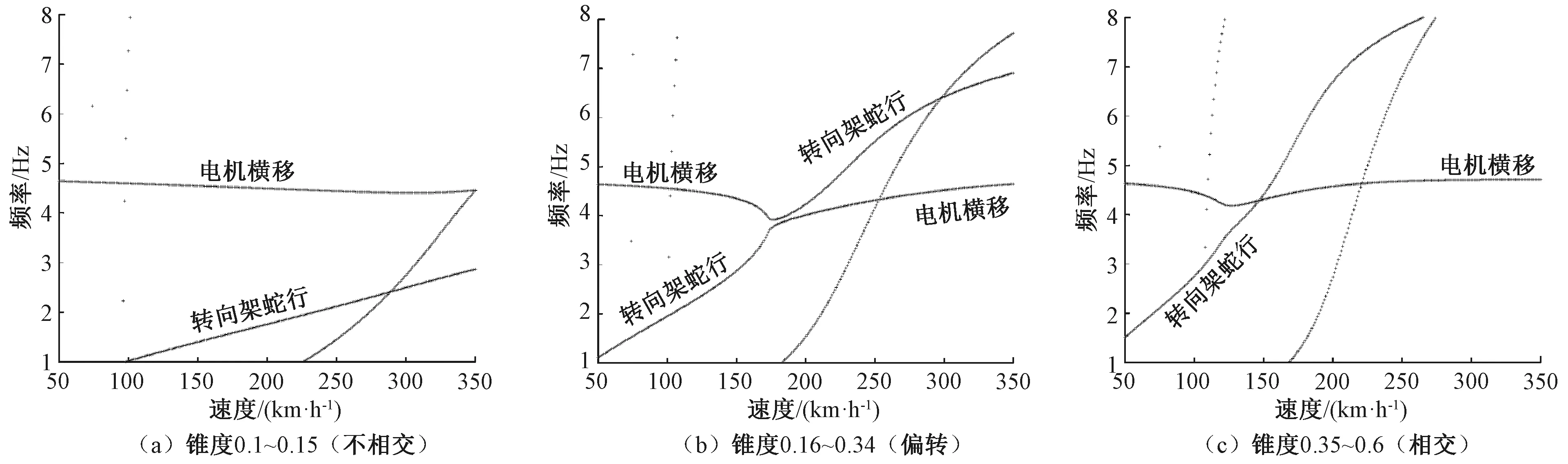
图7 频率轨迹演变趋势

为了验证转向架蛇行频率随等效锥度变化产生的跳变现象，采用Runge-Kutta积分方法进行时域仿真，分析冲击作用下转向架横向位移和横向加速度的时频域特征。图8给出了运行速度为350 km/h，等效锥度从0.25变化到0.45时，构架和电机横向位移的计算结果。可以看出，随着等效锥度的增加，转向架蛇行运动频率逐渐增加。等效锥度小于0.35时构架横向位移主频小于4.7 Hz，等效锥度大于0.35时构架横向位移主频大于7.3 Hz。等效锥度在0.35附近(临界等效锥度)，构架横向位移主频存在跳变现象，此时构架横向位移会同时存在两个主频，分别为4.7、7.3 Hz。由于构架横向加速度与频率的平方成正比，相对于构架横向位移而言构架横向加速度在高频时的能量会更加显著，因此从构架横向加速度来看(图9)，频率跳变会略有提前，等效锥度在0.3附近就会产生跳变，这与前期线路跟踪测试结果比较吻合。

图8 构架与电机横向位移的时域和频域分析

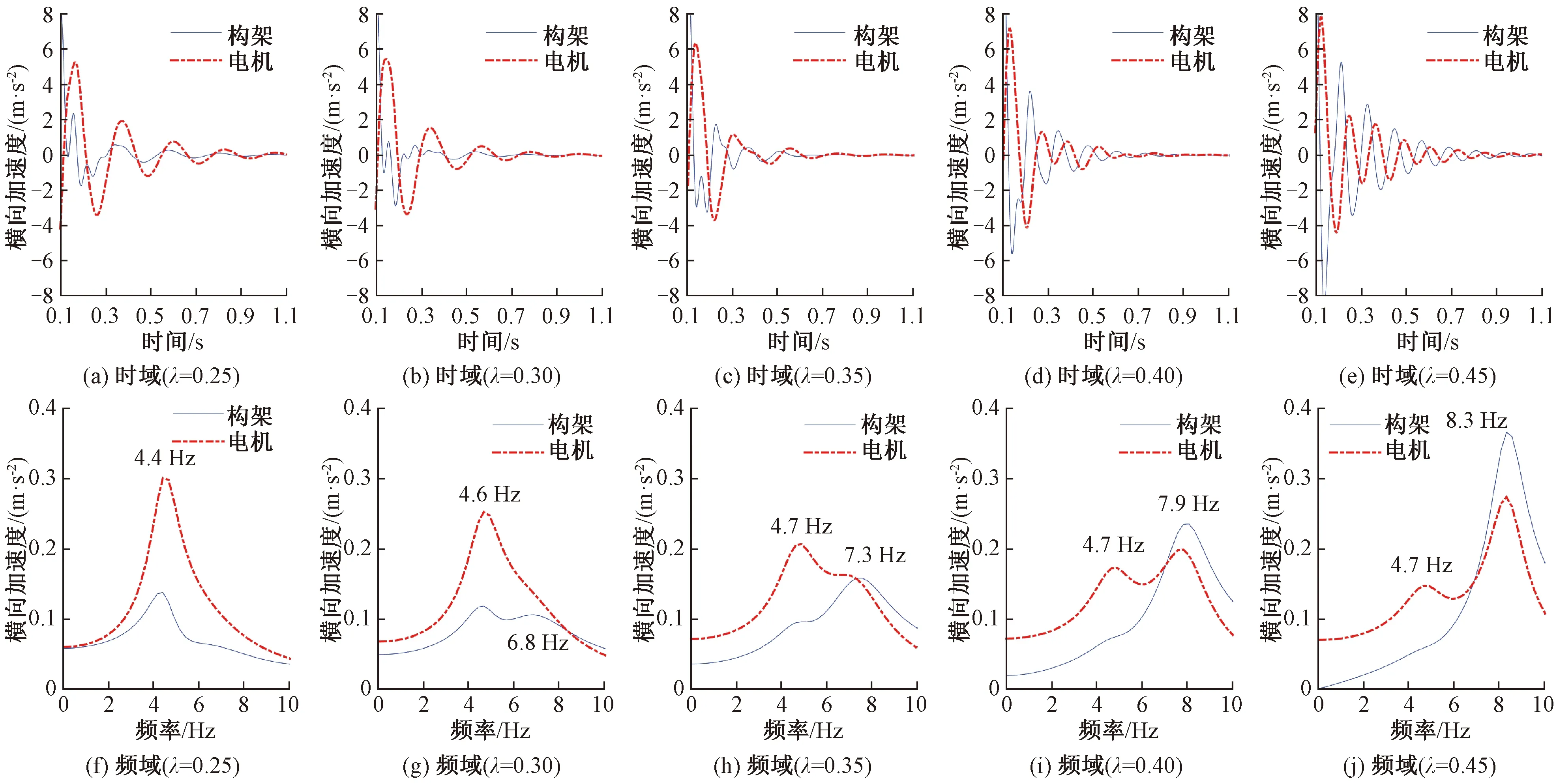
图9 构架与电机横向加速度的时域和频域分析

3 转向架蛇行频率跳变的影响因素

图10给出了电机横移频率和阻尼比对临界等效锥度的影响，其计算方法与图5相同，即利用根轨迹计算来搜索转向架蛇行频率跳变时的临界等效锥度。从图10(a)可以看出，电机横移阻尼比较小时(ζmy≤0.45)，蛇行频率存在跳变现象，电机横移频率越小蛇行频率跳变时的临界等效锥度越小。当电机横移阻尼比较大时(ζmy>0.45)，蛇行频率跳变现象消失，从图11给出的特征值随等效锥度变化曲线可以看出，这是由于电机横移阻尼比过大导致电机横移和转向架蛇行的耦合效应变弱引起的。从图10(b)可以看出，电机横移频率过小(fmy<3 Hz)或者过大(fmy>7 Hz)时，蛇行频率跳变现象也会消失。电机横移频率过小时转向架蛇行频率接近无电机模型，而电机横移频率过大时转向架蛇行频率接近电机固接模型(见图12)。

图10 电机横移频率和阻尼比对频率跳变的影响

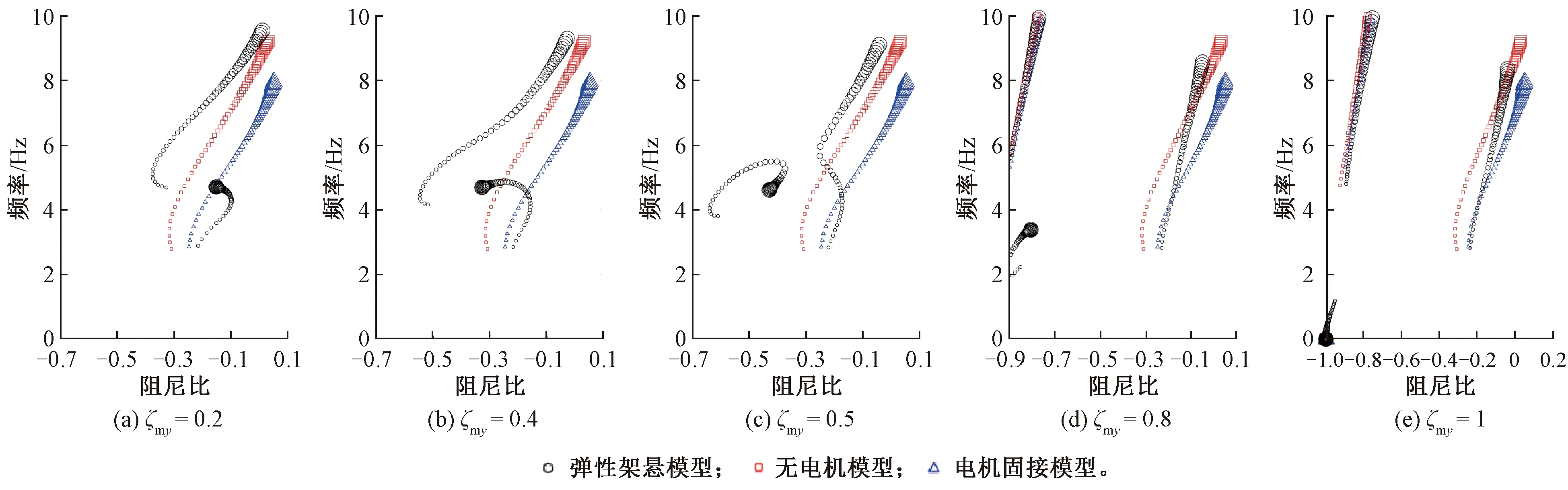
图11 不同电机横移阻尼比下特征值随等效锥度的变化曲线

图12 不同电机横移频率下特征值随等效锥度的变化曲线

为了验证电机架悬参数对转向架蛇行频率跳变的影响规律，采用Runge-Kutta积分方法进行时域仿真计算(运行速度350 km/h)，对时域信号进行频谱变换(FFT)后，给出不同电机横移频率和阻尼比下蛇行频率的变化规律。从图13可以看出，无电机模型的蛇行频率高于电机固接模型，其原因是电机固接模型的参振质量较大，等效锥度为0.3、0.4、0.5时，无电机模型的蛇行频率为6.6、7.8、8.6 Hz，而电机固接模型的蛇行频率为5.9、6.8、7.5 Hz。对于电机弹性架悬模型，电机横移频率越小，蛇行频率跳变时的等效锥度越小，频率跳变幅值也越小。当电机横移频率低到一定程度时，蛇行频率跳变现象消失，此时的转向架蛇行频率与无电机模型的蛇行频率接近，电机不再参与转向架的蛇行运动。当电机横移频率高到一定程度时，蛇行频率跳变现象也会消失，此时的转向架蛇行频率与电机固接模型的蛇行频率接近，电机和转向架如同一个整体展现同步的蛇行运动。等效锥度小于频率跳变对应的临界等效锥度时，电机弹性架悬模型的蛇行频率低于电机固接模型的蛇行频率，此时电机悬挂频率越低蛇行频率越小。在接近临界等效锥度附近，蛇行频率基本保持恒定，其数值接近电机悬挂的固有频率。当等效锥度超过临界等效锥度之后，电机弹性架悬模型的蛇行频率高于无电机模型的蛇行频率，此时电机悬挂频率越大蛇行频率越高。

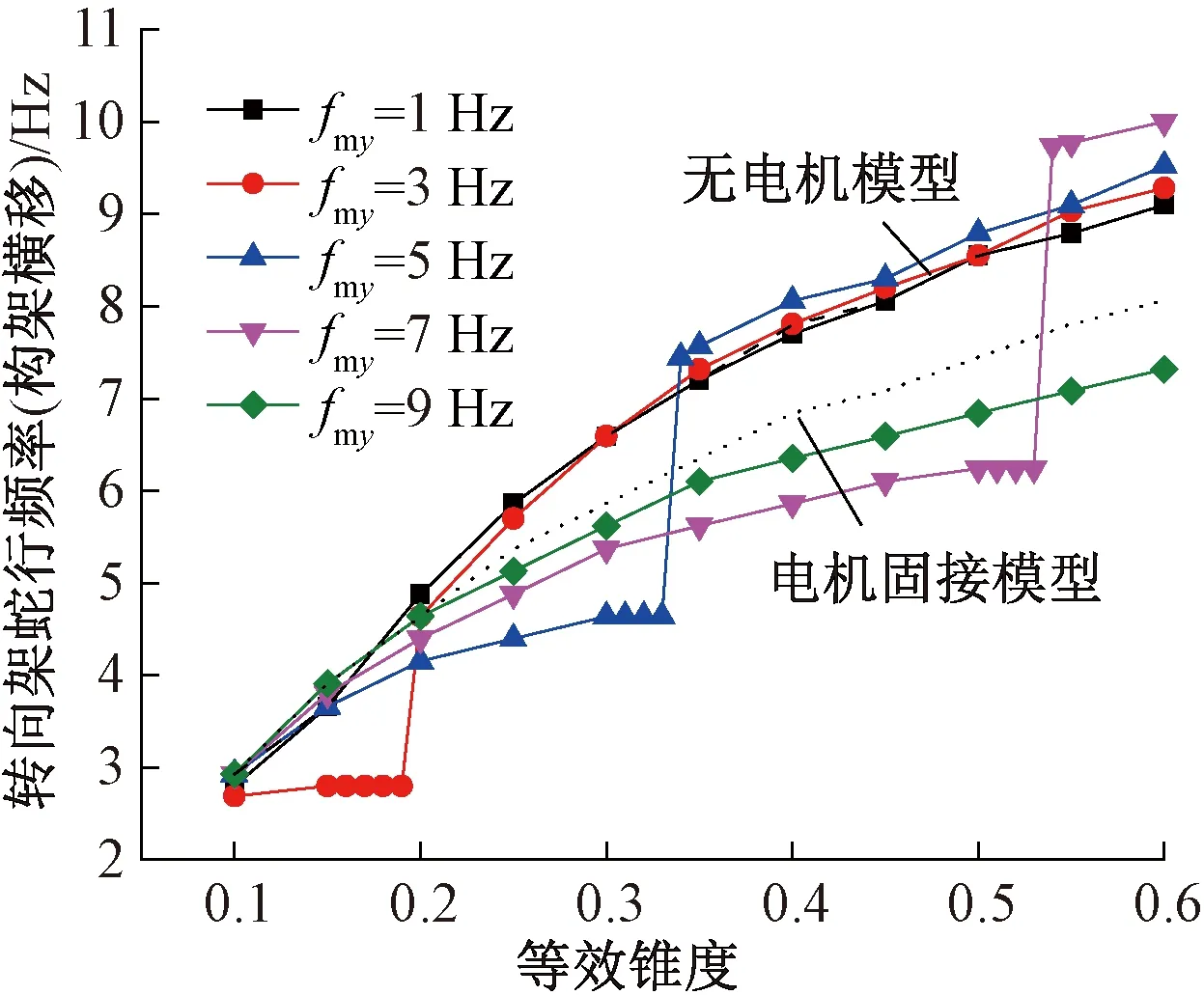
图13 电机横移频率对构架蛇行频率的影响(位移信号)

从图14可以看出，电机悬挂阻尼比较小时，频率跳变现象明显，阻尼比越小临界等效锥度越大，频率跳变幅值也越大；在等效锥度小于临界等效锥度附近，阻尼比越小蛇行频率越低；而等效锥度大于临界等效锥度后，蛇行频率产生跳变，阻尼比越小蛇行频率反而越高。电机阻尼比超过一定数值(ζmy>0.4)后，转向架蛇行频率呈连续变化趋势，频率跳变现象消失。

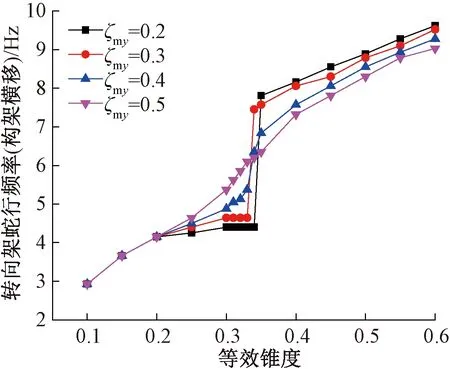
图14 电机横移阻尼比对构架蛇行频率的影响(位移信号)

图15给出了构架横向位移和横向加速度主频随等效锥度的变化曲线。可以看出，基于构架横向加速度得出的临界等效锥度略低于构架横向位移，频率跳变幅值也略低。

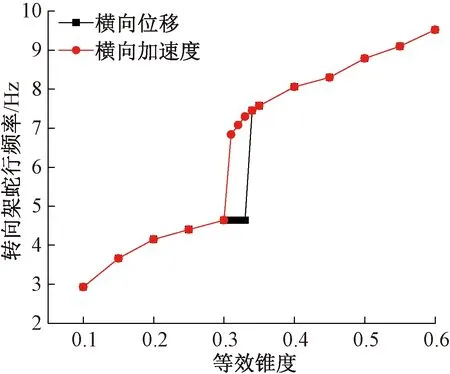
图15 构架横向位移和横向加速度的主频对比

4 结论

(1)一个镟轮周期内随着等效锥度的增加，无电机模型和电机固接模型的转向架蛇行频率呈连续变化趋势，而电机弹性架悬转向架蛇行频率可能存在跳变现象，其存在条件取决于电机架悬参数。电机横移频率过小或者过大，转向架蛇行频率跳变现象消失；电机横移阻尼比过大，转向架蛇行频率跳变现象也会消失。

(2)电机架悬参数满足转向架蛇行频率跳变条件时，电机横移频率越小，蛇行频率跳变时的临界等效锥度越小，频率跳变幅值也越小；电机横移阻尼比越小，蛇行频率跳变时的临界等效锥度越大，频率跳变幅值也越大。根据理论分析和线路跟踪试验，本文研究的动车转向架蛇行频率跳变条件时的临界等效锥度约为0.3。

(3)等效锥度小于频率跳变对应的临界等效锥度时，转向架蛇行频率低于电机固接模型，电机横移频率和阻尼比越小蛇行频率越小；等效锥度大于临界等效锥度时，蛇行频率高于无电机模型的蛇行频率，电机横移频率越大蛇行频率越大，电机阻尼比越小蛇行频率越大。

由于轮轨匹配等效锥度不受人为控制，电机悬挂刚度也较难改动，为了消除电机弹性架悬高速转向架蛇行频率的跳变现象，可以通过增加电机减振器阻尼系数来现实，建议将电机横移阻尼比增加至0.5。