高速铁路轨道短波健康状态动态诊断模型和方法

刘金朝，徐晓迪，牛留斌，孙善超，张二永，赵 钢

(1.中国铁道科学研究院集团有限公司 基础设施检测研究所, 北京 100081；2.中国铁道科学研究院集团有限公司 铁路基础设施检测中心, 北京 100081)

随着我国高速铁路服役时间的增加以及高速铁路列车运营速度的逐级提高，对轨道-车辆系统平稳性的要求也越来越严格。而直接决定高速铁路轨道-车辆系统是否能够平稳安全运行的一个重要因素就是轨道的平顺性状态[1]。根据波长，轨道平顺性状态可分为长波、中波和短波三种类型的轨道不平顺。其中病害波长分布在1 m以下的为轨道短波不平顺，其对应的病害幅值较小，一般分布在几个毫米范围之内。高速铁路轨道短波不平顺在钢轨表面主要表现为钢轨焊接接头不良、钢轨擦伤、硌伤或钢轨波磨等。传统的轨道几何检测系统检测的有效波长通常在2～150 m 之间，高速铁路1 m以下的钢轨波磨、焊接接头凸凹不平、道岔状态不良等短波不平顺引起的的高频振动对轨道-车辆系统运行状态造成的影响难以评判，为此需要研究其他辅助评判手段进行检测。

作为刚性体，车辆的轮对与轴箱直接相连，轨道短波不平顺引起的高频振动响应可以直接传递到轴箱上。因此，轴箱加速度可用于评判轨道短波状态，并反映其引起的外界激扰对轨道-车辆系统的影响。文献 [2]指出，利用轴箱加速度检测轨道短波不平顺具有容易操作、维护方便、经济实用等诸多优点。文献[3]采用小波包变换对轴箱加速度进行了分析，并针对轨道短波不平顺引起的轴箱加速度在不同带宽内的振动成分的时间-尺度谱进行了计算。文献[4-6]利用加速度的能量谱诊断了钢轨波磨。文献[7-8]对新干线某一小半径曲线上钢轨接头引起的轴箱加速度特征进行了分析，最后指出针对不同类型的轨道短波病害应选择不同的频带分别对轴箱加速度进行处理。文献[9]通过计算轴箱加速度的功率谱对钢轨表面的粗糙度进行了计算。为了研究轨道短波探测方法以及轨道短波不平顺与轴箱加速度之间的关系，文献[10]建立了轮轨系统的有限元模型。为了表征轨道短波伤损大小，文献[11]利用尺度平均化的小波功率 (Scale Averaged Wavelet Power，SAWP)对轴箱加速度数据进行了处理。康熊等[12]利用广义共振解调方法，将车辆-轨道系统的低频特征转化为对轴箱加速度高频共振的分析，提出了高速铁路焊接接头状态的动态评判方法和实现方式。刘金朝等[13]提出了评判轨道短波状态的轨道冲击指数法，为冲击性病害的评判制定了严格的方案。

本文利用时间-频率联合的方法，从能量的角度刻画了钢轨波磨等高速铁路轨道短波病害所引起轴箱加速度数据的高频振动特性，并提出基于车辆动态响应的集成轨道冲击指数(Track Impact Index，TII)和波磨指数(RCI)的高速铁路轨道短波状态动态诊断方法，以及轨道-轮对系统高频仿真模型，最后利用实测数据对模型和方法进行验证。

1 轨道短波状态时频特性分析

高速综合检测列车上的车辆加速度检测系统可实时采集列车在运行过程中车辆的车体、构架和轴箱等各个位置在横、纵、垂等各个方向的振动加速度。该检测系统采用多通道分布式网络化测试技术，远距离协同操作保证了数据采集的实时性和可靠性。

时频谱可以将信号表示为时间-频率的联合分布函数，清楚地描述非平稳信号频率随时间的变化。1946 年提出的Gabor 变换奠定了在时间和频率联合域内分析信号的理论基础[14]。1947 年Potter 等[15]提出了简单而实用的短时傅里叶变换(STFT)。然而，由于不确定原理的限制，STFT不能兼顾频率和时间分辨率的需求。Wigner-Ville 分布的时频聚集度较高[16]，但遗憾的是Wigner-Ville 分布不能保证非负性，而且对多分量会产生严重的交叉干扰，使其谱分布难以解释，严重限制了它的广泛应用。2010年，Thakur等提出了同步压缩短时傅里叶变换(SSTFT)的方法[17]。该方法是一种时频重排的算法，同时支持信号的重构。基于该方法的时频表示和瞬时频率提取步骤如下：

Step1对于待分析信号f(t)，给定窗函数g，进行STFT变换,即

(1)

式中：t为时间；η为时移参数；ξ为频率。

Step2计算f(t)的瞬时频率，即

(2)

Step3根据Step2中计算得到的瞬时频率，对Step1的计算结果进行时频重排，即同步压缩：

(3)

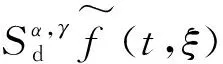
波磨区段钢轨表面平直度和功率谱分别见图1(a)、1(b)，利用SSTFT 方法对波磨区段的轴箱加速度进行分析，其时频谱见图1(c)。从图1可以看出，波磨区段钢轨表面平直度和轴箱加速度波形呈现周期性。该区段波磨的波长为150 mm；轴箱加速度主频为561 Hz，运行速度为304 km/h，通过换算可知，其对应的波长与 150 mm 很接近。轴箱加速度能较好反映钢轨波磨的特性，而且对应的波长也是一致的，轮对系统呈现近似线性振动特性。

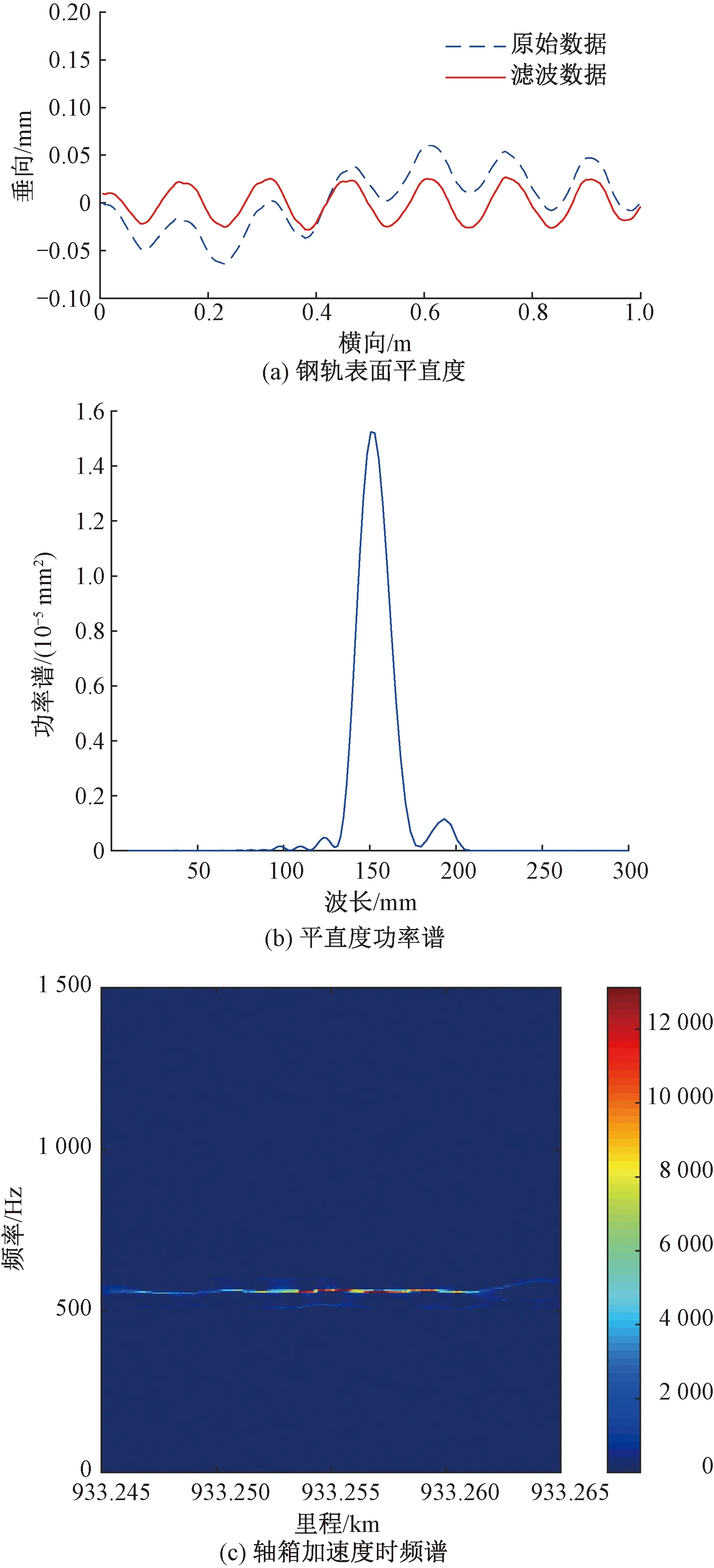
图1 波磨区段钢轨表面平直度和功率谱以及对应的轴箱加速度时频谱

留有打磨痕迹的钢轨表面平直度和功率谱分别见图2(a)、2(b)，利用SSTFT 方法对打磨痕迹区段的轴箱加速度进行分析，其时频谱见图2(c)。从图2可以看出，打磨痕迹区段钢轨表面平直度和轴箱加速度波形呈现周期性。该区段波磨的波长为75 mm；轴箱加速度主频为 562 Hz，运行速度为304 km/h，通过换算可知，其对应的波长与 150 mm 很接近。打磨痕迹区段，轴箱加速度对应波长是实测打磨痕迹波长的2倍，轮轨系统呈现非线性振动特性。

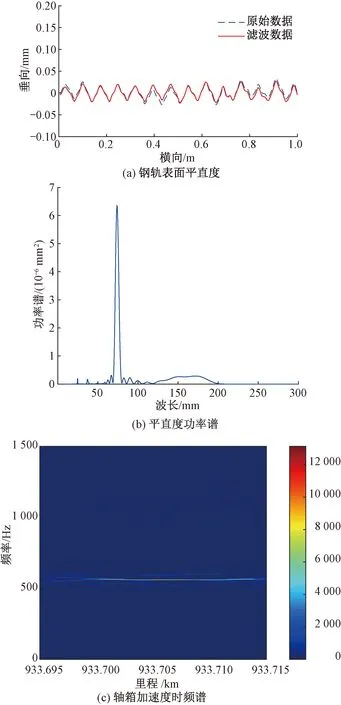
图2 留有打磨痕迹区段钢轨表面平直度和功率谱以及对应的轴箱加速度时频谱

2 轨道-轮对系统高频仿真模型

应用有限元软件Abaqus建立三维高速轮轨有限元模型，见图3。该模型采用直径为860 mm的LMA型踏面车轮。轨道设置为无砟轨道，由于应力波效应会对钢轨两端的计算结果产生影响，同时轨道扣件整体刚度及阻尼也会导致计算结果的变化，所以将轨道进行延长，全长设为15.21 m，车轮实际滚过轨道长度为3.7 m。轨枕间距为0.65 m。钢轨廓形为CN60，轨底坡设为1/40，钢轨表面设有波浪磨耗，区段长度为1 m，波长为80 mm，波深0.14 mm。考虑轮轨滚动接触过程中，由静态到动态过渡时会出现初始激扰，而且这种现象会随速度增加更加明显，所以需要在计算工况前面设置一松弛区域避免此类状况，本模型中，松弛区域的长度为2.4 m。

图3 轨道-车辆系统高频有限元模型

通过Matlab软件修改数据文件加入钢轨波磨，利用Abaqus/Explicit软件进行计算，设定的计算条件为轨道短波不平顺的幅值从0.02 mm递增到0.2 mm、波长从25 mm递增到400 mm、车辆的运行速度从210 km/h递增至360 km/h。在该条件下轨道短波不平顺引起的动态轮轨垂向力结果见图4。从图4可以看出，在车辆运行速度相同的情况下，动态轮轨垂向力会随着轨道短波不平顺幅值的增加而变大，但两者并不呈现线性增长关系；同时，当轨道短波不平顺的幅值不变时，动态轮轨垂向力呈现随着波长的增加先急剧增大后再缓慢减小的特征，该特性说明在轨道短波不平顺的波长不相同时，动态轮轨垂向力的敏感程度不同。

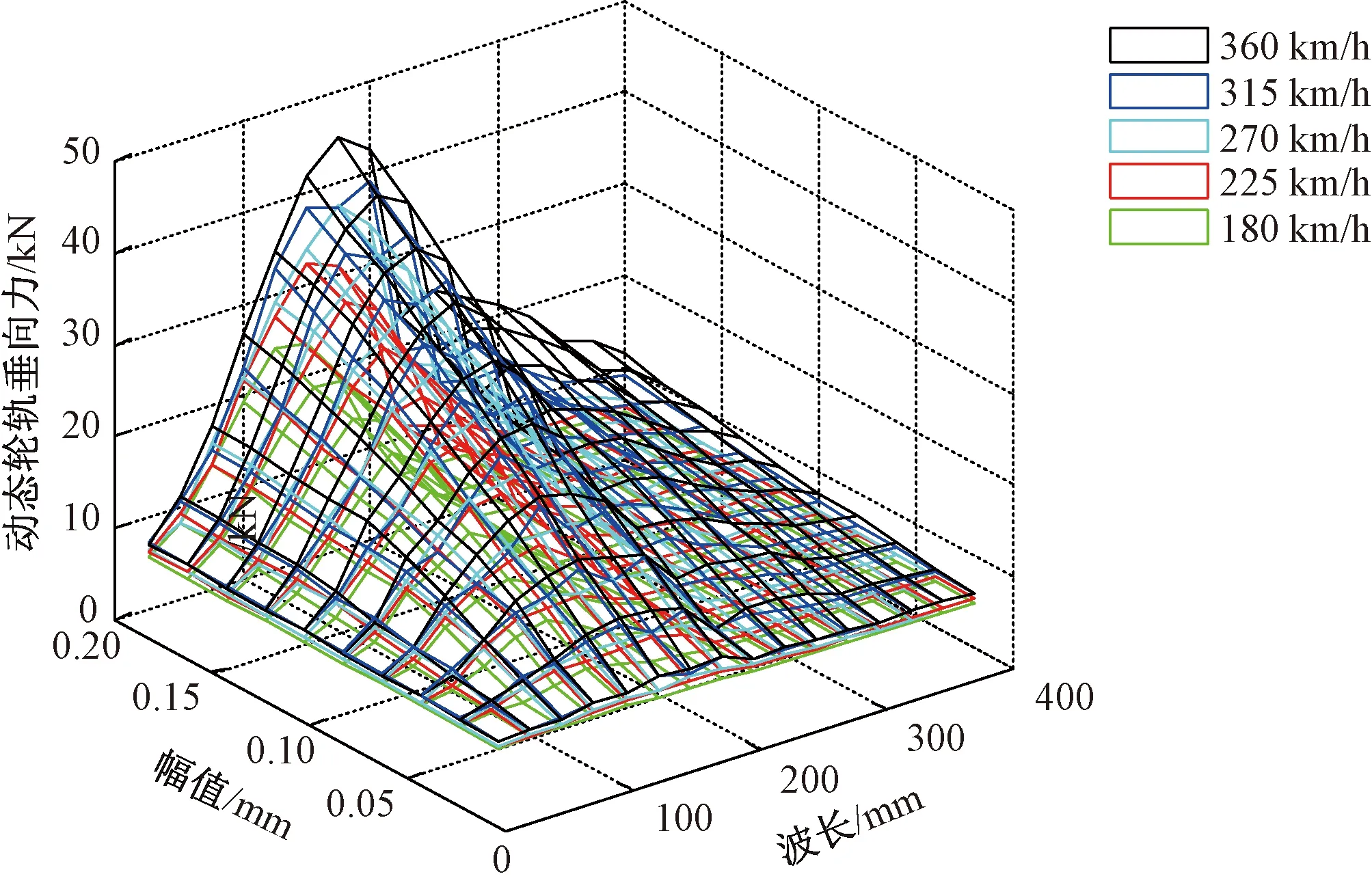
图4 轨道短波不平顺条件下的动态轮轨垂向力

3 基于能量的高速铁路轨道短波状态动态诊断方法

车轮踏面及钢轨踏面的形状和材料、车辆悬挂参数、传感器的安装位置等因素对轴箱加速度幅值的影响较大，最直接体现就是，当这些参数改变时，计算所得轴箱加速度的移动有效值的平均值会呈现明显的变化。为避免以上情况对轨道短波状态评判造成影响，将计算所得移动有效值进行归一化处理，即使用轨道冲击指数(Track Impact Index，TII)和波磨指数(Rail Corrugation Index, RCI)评判轨道的短波不平顺状态。

不同类型轨道短波病害的带通滤波范围依据第2节的时频分析方法进行确定。记带通滤波后的轴箱加速度信号为{xi|i=1,2,…,N}，其中N为信号的长度，最终计算所得轴箱加速度的移动有效值记为{Sr|r=1,2,…,N-K+1}，其中

(4)

式中：K为移动窗长。

综合检测列车采集所得的轴箱振动加速度是高频信号，通过解调计算得到的移动有效值是低频信号，该计算过程与信号的光滑化处理过程类似。同时，由于低频信号与高频信号相比稳定性较高，因此不同时间多次检测得到的轴箱加速度即便呈现很高的随机性，最终所计算得到的移动有效值波形差异也会较小。

定义轨道冲击指数tTII为带通滤波后轴箱加速度的移动有效值与其平均值的比值，其计算过程可表达为

(5)

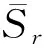
钢轨波磨指数rRCI的定义与轨道冲击指数tTII类似，为带通滤波后轴箱加速度的移动有效值与其平均值的比值。由波磨区段的谱分析可知，速度350、250 km/h高速线路呈现拟周期性的疑似波磨区段的波长一般分布在30～150 mm范围内，根据频率、速度和波长的换算关系，确定计算波磨指数的带通滤波频率，根据钢轨波磨引起的振动响应的长度确定计算窗长，并通过计算振动响应数据的能量指标以及归一化参数得到钢轨波磨指数。由于钢轨波磨引起的振动响应呈现拟周期性，利用轴箱加速度的能量因子刻画其在疑似波磨波长对应的频率附近的能量集中特性。其由主频附近3 Hz内的能量与总能量的比值计算得到，对应区段轴箱加速度的能量因子越大，说明钢轨波磨引起的周期性振动特性越强，即钢轨表面的波磨特征越明显。定义能量因子E为轴箱加速度第一能量峰值处的能量与其总的能量的比值，即

(6)

式中:Ep、Es分别为轴箱加速度第一能量峰值处的能量、总能量。

4 试验验证

4.1 焊接接头不良

利用高速综合检测列车实测的某高速铁路的轴箱加速度数据，计算轨道冲击指数，结果见图5。由于各峰值的间距为100 m，初步推断该处短波病害为钢轨焊缝不良。

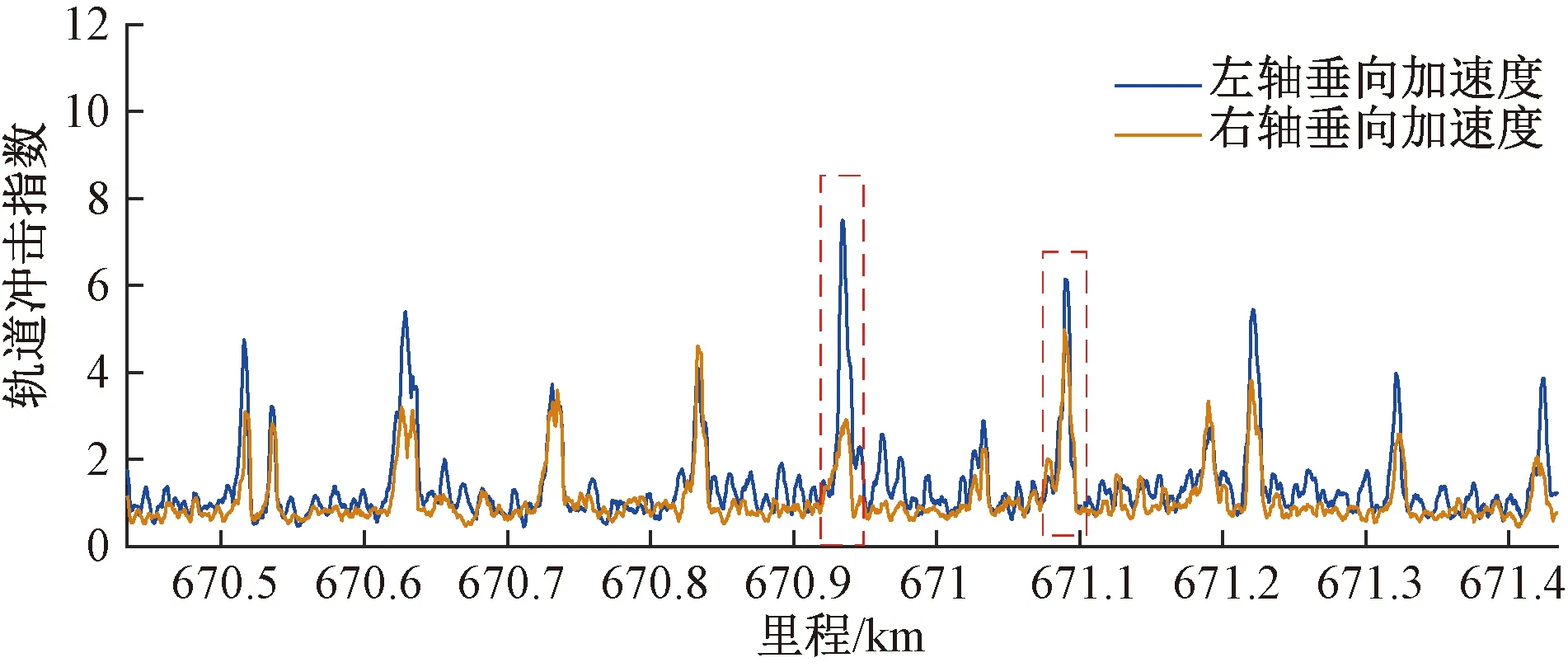
图5 K670+934附近的轨道冲击指数

现场复核图片和利用电子平直度仪测得的钢轨行车面平直度见图6。由图6(b) 可以看出该处钢轨行车面平直度最大值为0.362 mm，超过焊缝限值 0.2 mm，与诊断结果吻合。

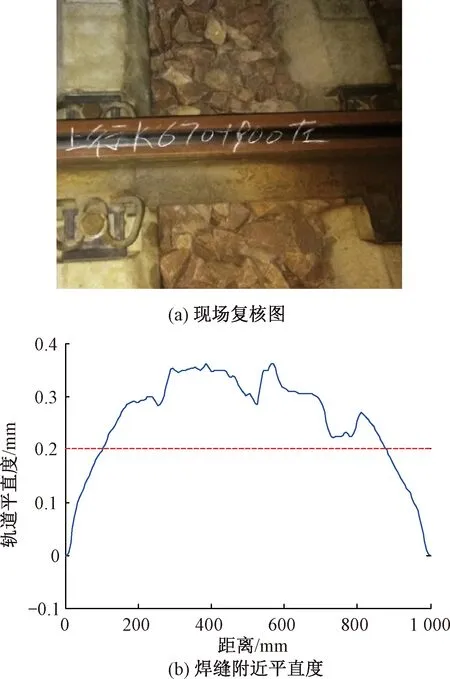
图6 某高速铁路上行K670+900处现场复核图和焊缝附近平直度

4.2 钢轨波磨

利用高速综合检测列车实测的某高速铁路下行K932+879—K932+921区段的轴箱加速度进行计算，结果见图7。计算可知，其波磨指数达到8.2；从图7可以看出，能量集中因子达到了0.6,该区段响应数据波长主要集中在157 mm，诊断该处可能存在波磨。

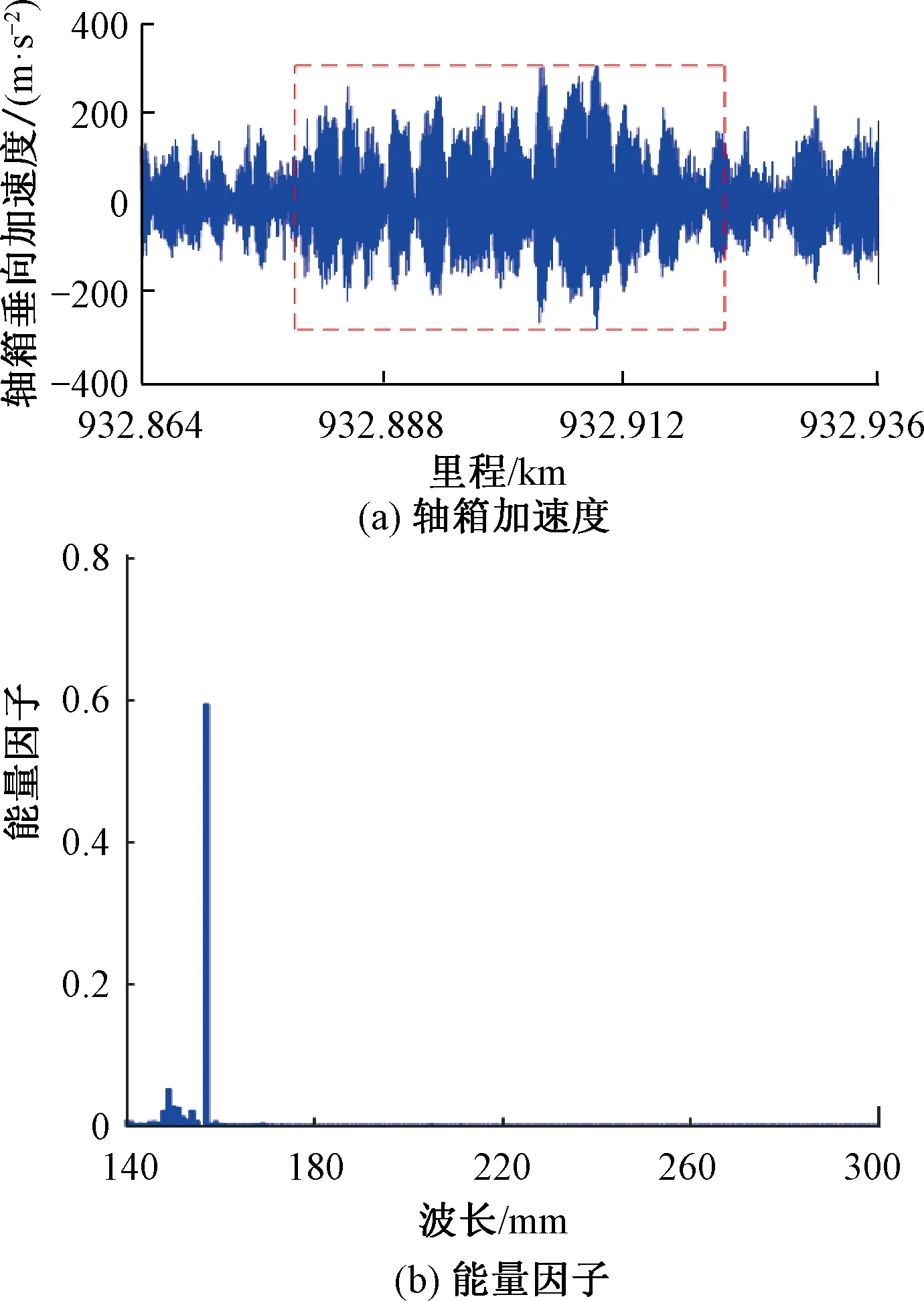
图7 某高速铁路下行K932+879—K932+921区段右侧轴箱加速度波形和能量因子

下行K932+920附近左轨轨面平直度波形及其空间频谱见图8。从图8可以看出：平直度最大值为0.034 mm，最小值为-0.027 mm；滤除趋势项以后平直度最大值为0.027 4 mm，最小值为-0.022 2 mm；峰峰值为0.047 6 mm。74 mm波长成分能量较强，与动态响应波长呈现倍频关系。钢轨表面存在打磨痕迹见图9。

图8 K932+920下行左轨轨面平直度波形和空间频谱

图9 K932+920下行右轨打磨痕迹

5 结论

随着更多高速铁路的建设运营，轨道短波病害对车辆轨道系统的影响逐渐受到人们的重视。高速铁路轨道几何检测波长通常在2～150 m之间，难以发现钢轨焊接接头不平顺、钢轨波磨、擦伤、硌伤或剥离掉块等波长1 m以下的轨道短波病害。利用轴箱加速度可从对车辆运行影响角度对这些问题进行检测及评判，从而对传统轨道几何检测进行补充。本文提出基于带通滤波后的轴箱加速度的轨道冲击指数(TII)和波磨指数(RCI)，用于轨道短波不平顺病害的诊断。现场复核结果表明，新的诊断方法能有效识别焊接接头不良、钢轨波磨等轨道短波病害，完善了轨道平顺性的评判体系。