某加热炉炉管的数值计算与寿命预测

吕鑫，王正，王璐

（116024 辽宁省 大连市 大连理工大学 能源与动力学院）

0 引言

加热炉作为整个重油催化加氢的重要设备，内部炉管的可靠服役年限和安全性指标是其长期稳定运行的重要保证。对炉管的研究包含了模型设计、材料选择、结构排布、约束位置以及蠕变寿命等诸多方面。既要使炉管能将渣油加热到加氢裂化反应所需温度，又要让选取的炉管材料（TP347H）可以在高温高压的加热炉内安全运行[1]。

本文以对流室炉管为研究对象，首先利用Flunet 求解管内流场，得到流固耦合面的温度场、压力场、出口流体温度以及压力降；之后，把前者作为载荷条件加入到炉管温度场、应力场分析中，分别求解热应力场和温度-压力耦合应力场，找出应力最大的危险位置，并与理论计算值比较；最后，将最大应力值带入L-M 方程并完成对流炉管的寿命评价。

1 管内流体有限元模型的建立

通过ANSYS Workbench 的DM 建模功能实现对流炉管内部流体域的填充，生成三维流体模型。进入Mesh 模块，采用四面体网格划分方式，并对弯头处进行网格加密。经检验，平均网格质量达到0.837，共有993 371 个网格元素，218 243个网格结点。整个流体域的有限元模型如图1 所示，弯头处流体网格模型如图2 所示。

图1 流体域有限元模型图Fig.1 Finite element model diagram of fluid field

图2 弯头处流体网格图Fig.2 Fluid grid model diagram at elbow

2 基于Fluent 的流场分析

2.1 流场模拟参数设置

设置流体（Fluid）材料为渣油（Oil），并准确定义渣油的相关参数。选择稳态模式进行分析，打开能量方程并选择k-ε二方程黏性流体湍流模型求解，流动边界条件设置如表1 所示。

表1 流场边界条件加载Tab.1 Boundary condition loading of flow field

2.2 流场模拟分析

2.2.1 流速分布结果

经计算，整个流体域速度矢量分布如图3 所示，出口截面流体速度分布如图4 所示。从图3中可看出，弯头处的流体速度明显大于其他位置，速度最大值为2.92 m/s，这是当流体流经弯头时，流动截面变化产生局部扰动造成的。从图4 可以看出，流速从贴近壁面到炉管轴线附近逐渐变大，这也解释了流体的黏性作用，存在速度边界层。

图3 流速分布矢量图Fig.3 Vector diagram of velocity distribution

图4 出口截面的速度云图Fig.4 Velocity nephogram of exit section

2.2.2 流体压力分布

管内流动着高压（P＞10 MPa）渣油，已经进入高压管道的研究范畴。如图5 所示，入口处压力值最高，达到了11.5 MPa。压力从炉管入口到出口实现了递减，压降约为0.1 MPa。这说明工质在流动过程中受到了沿程黏性摩擦阻力和弯头处局部阻力，产生了较大的能量损失。由图6 可以看出，近壁处流体的压力值较大，越靠近管道轴线，流体压力越低；近壁处渣油在黏性摩擦力的作用下低速流动，相反，轴线附近流体流速较大。因此，流体速度越大，压力越低。

图5 流体压力云图Fig.5 Pressure nephogram of fluid

图6 入口截面的压力云图Fig.6 Pressure nephogram of inlet section

2.2.3 流体温度分布

图7 流体温度云图Fig.7 Temperature nephogram of fluid

渣油出口温度是炉管换热好坏评价的重要参数，它决定了后续渣油加氢裂解反应能否顺利进行。由图7 可以发现，高压渣油流经炉管后，温度逐渐从入口的320 ℃升高到出口的358 ℃，温升为38 ℃，符合对流室炉管的设计要求。图8是出口截面的流体温度分布，贴近管外壁处的流体温度较高，近管子轴线处的流体温度较低，这种现象是由渣油内部存在导热过程造成的，热量要从管内壁流体向管子轴线处流体传递。

图8 出口截面的温度云图Fig.8 Temperature nephogram of outlet section

3 炉管应力理论计算

3.1 炉管内部压应力

当内部流体介质的压力作用在炉管内壁时，管子各结点所受应力可分解为3 个方向，即轴向应力、径向应力以及周向应力。根据管道设计手册，当do/di≤1.2 时，管子可以当做薄壁管进行计算[2]。因为炉管的设计尺寸为 Φ168×14 mm，168/154 ≤1.2，所以沿半径的压应力σr可以忽略，只有σθ，σz两个方向的应力。压应力计算公式可以简化为

式中：σr——径向应力；σθ——周向应力；σz——轴向应力；do——炉管外径；di——炉管内径；P——管内压；d——结点直径。

3.2 炉管内部热应力

炉管内部的热应力也分成σr，σθ，σz三种，根据相关力学公式推导，得到3 种应力计算方程：

根据炉管材料（TP347H）相关物性参数，线膨胀系数α=15.8×10-6K-1，弹性模量E=200 GPa，泊松比μ=0.28，Δti接近50 ℃。经计算，得到如下应力结果：

可见，炉管热应力要比压应力大很多，所以，在炉管的安全性设计上应更多地考虑热应力的影响[3]。

4 炉管应力的模拟分析

4.1 炉管热应力的数值计算

4.1.1 对流炉管有限元模型的建立

继续采用非结构性网格划分方式划分网格。由于弯头处容易发生损伤破坏，所以继续对弯头进行网格加密细化。平均网格质量达到了0.782，共有 731 769 个网格元素，1 365 027 个结点。整个对流加热炉管的有限元模型如图9 所示，弯头位置加密后的网格模型如图10 所示[4]。

图9 对流炉管有限元模型图Fig.9 Finite element model diagram of convection furnace tube

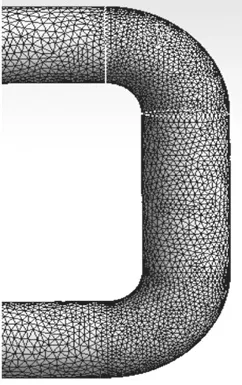
图10 炉管弯头处网格模型Fig.10 Grid model of furnace pipe elbow

4.1.2 炉管的稳态热分析

对流炉管温度场模拟计算，为耐温抗蠕变材料的选取、管内热应力的分析提供重要依据。将在Fluent 里面得到的流固耦合面温度作为温度载荷，如图11 所示，研究对流炉管温度分布，同时，设置管外壁的对流换热系数和环境温度。由于对流段炉管和高温烟气之间存在强制对流换热，管外壁最高温度已经达到了400 ℃，如图12 所示，这样的温度已经满足管材TP347H 的蠕变起始条件，因此，要讨论计算该炉管的寿命。

图11 流固耦合面的温度载荷Fig.11 Temperature load on fluid-solid coupling surface

图12 炉管温度云图Fig.12 Temperature nephogram of furnace tube

4.1.3 炉管的应力场分析

应力场是对炉管进行安全评价和寿命预测的重要参考量，本文使用Static Structural 计算炉管内部应力分布。首先，导入从稳态热模块获取的炉管温度场，将其作为温度载荷加载进来，如图13 所示；之后，对炉管施加边界约束条件，进口截面施加Y 方向的位移约束，出口截面施加Z方向的位移约束，对直管段的中心轴线施加X 方向位移约束，并得到了在温度载荷下的应力、应变和变形分布图[5]，分别见图14—图16。

图13 温度载荷的加载Fig.13 Loading of temperature load

图14 中，炉管弯头位置存在热应力最大值，为156.94 MPa。而且弯头附近应力高出直管段很多。同时，弯头位置也存在最大应变值，高达0.1%，如图15 所示。该位置已经发生了塑性变形，因此，炉管弯头处极容易发生应力破坏。由施加的位移约束导致炉管左上角的变形高于右下角，最大变形量为39.7 mm，如图16 所示。

图14 温度载荷作用下的应力云图Fig.14 Stress nephogram under temperature load

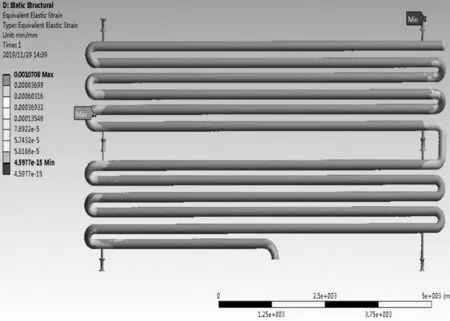
图15 温度载荷作用下的应变云图Fig.15 Strain nephogram under temperature load

图16 温度载荷作用下的变形云图Fig.16 Deformation nephogram under temperature load

4.2 温度-压力耦合下的炉管应力

为了验证渣油内压力对管道应力的影响大小，如图17 所示，在温度载荷的基础上施加前面得到的流固耦合面的压力，其它参数设置保持不变，继续计算温度-压力耦合载荷作用下的炉管应力、应变和变形。

在温度-压力耦合载荷作用下，得到流炉管的应力云图，如图18 所示。依旧是在炉管弯头处存在最大应力值，为172.48 MPa。这和温度载荷单独作用下的热应力最大值156.94 MPa 相比没有增加很多，说明压力载荷作用对炉管应力影响较小，主要还是炉管热应力的作用导致材料失效。此时，弯头的应变也达到了最大，为0.11%，如图19 所示。炉管变形量的分布和前面得到的变形云图相似，如图20 所示。变形最大值变为54.1 mm，耦合载荷作用导致了变形量的增加[6]。

图17 压力载荷的加载Fig.17 Loading of pressure load

图18 温度-压力载荷作用下的应力云图Fig.18 Stress nephogram under temperature-pressure load

图19 温度-压力载荷作用下的应变云图Fig.19 Strain nephogram under temperature-pressure load

图20 温度-压力载荷作用下的变形云图Fig.20 Deformation nephogram under temperature-pressure load

5 炉管的寿命预测

5.1 蠕变损伤机理

由于加热炉炉管材质长期处于500 ℃左右的工作环境中，在管内渣油内压产生的一次应力和热应力的共同作用下，管材（TP347H）逐渐发生塑性应变。弯头处的材料更容易在高温下开始蠕变，开裂失效。

5.2 基于Larson-Miller 法的寿命估计

根据同组高温蠕变实验的相关数据，通过高阶拟合得到炉管材料的L-M 参数方程

式中:T——温度；σ——应力；tr——设计寿命；C 取21[7]。

将弯头位置的最大应力值172.48 MPa、温度500 ℃带入式（8）。经计算，对流炉管的蠕变寿命为5.0×106h。

6 结束语

通过对加热炉管的仿真计算和理论分析，得到了炉管内部的流场、炉管的温度场以及应力场。弯头处的应力和渣油流速都较大，是结构安全性研究的主要部位。

经过对比，流体内压产生的应力对炉管的应力场影响较小，热应力才是引起炉管损伤破坏的主要原因。

根据L-M 方程，得到炉管的蠕变寿命。这既能满足渣油出口温度的要求，又可以让加热炉管正常运行5.0×106h。