基于多态模糊BN的石化动设备故障概率定量风险评估

黄艾丹，李长俊，吴 瑕，王玉江

(1.西南石油大学石油与天然气工程学院，四川 成都 610500；2.中国石油化工股份有限公司胜利油田分公司，山东 东营 257000)

石化行业中，压缩机、泵这类由驱动机带动的转动设备称为动设备，相比于其他设备，动设备的精细化和自动化程度较高，故障模式更加复杂多样。由于处于易燃易爆、高温或高压的危险环境中，动设备的故障可能会带来灾难性后果。为了提高动设备的可靠性，通过已发生的故障模式推算出动设备故障的概率，可为企业检修提供决策信息，从而延长设备工作寿命，降低企业生产成本。

在国内外站场风险评估技术定量化发展的趋势下，已有研究利用基于风险的检测(RBI)方法对动设备进行了定量风险评估，但RBI方法主要针对泄漏、破裂引发的失效，由于动设备的故障模式多样，RBI方法应用于动设备风险评估略显粗糙。因此，也有研究利用故障模式与影响分析(FMEA)方法对压缩机和油轮各故障模式发生概率的风险等级进行了定量评估。该方法的优点是可以识别设备的潜在故障模式和影响，但多借助专家经验评判出各故障模式的风险等级，未考虑各故障模式之间以及故障模式与子系统或动设备故障之间的联系。

贝叶斯网络(Bayesian Network,BN)是目前常见的定量风险评估工具，不仅可以表示风险事件之间的因果关系，还可以通过条件概率表(Condition Probability Table,CPT)表征风险事件之间的依赖关系。与传统失效概率计算方法相比，BN最大的优势在于可以处理事件间的不确定性关系，由于风险事件的影响关系不只是0或1，根据事件间的依赖程度，CPT中可设置为0～1中任意概率数，因此BN广泛应用于复杂系统的可靠性评估和故障诊断等领域。如已有研究分别利用BN对导航和卫星等复杂系统进行了风险分析，但由于其难以获取条件概率和精确的失效数据，尚未有应用于石化行业动设备定量风险评估的相关案例。

针对上述问题，本文基于BN可定量计算复杂系统失效概率的特点，利用FMEA方法分析结果之间的逻辑关系，将其映射为BN来实现石化行业动设备故障概率的定量风险评估，并利用BN中节点的多态来展现动设备子系统及零部件故障模式的多样性。由于动设备零部件的故障概率存在不确定性，为了进一步提高评估模型的准确性，将BN边缘概率精确值替代为模糊概率子集，同时利用模糊层次分析法简化了专家构造CPT的难度，避免了直接根据专家知识及经验的定性判断。

1 基于FMEA和多态模糊BN的石化动设备故障概率定量风险评估模型构建

1.1 FMEA方法和多态模糊BN简介

故障模式与影响分析(Failure Modes and Effects Analysis,FMEA)方法或技术可用来识别潜在故障模式和影响，提高复杂系统的可靠性。FMEA方法通过系统地分析所有可能的故障模式、故障原因和影响，再依据各部位风险等级，依照轻重缓急程度指定改进措施。由于石化动设备的结构复杂、故障模式多样，且内部零部件之间的关联性较强，故本文采用FMEA方法分析其可能发生的故障模式和影响。但由于该方法分析过程中存在较多不确定因素，无法定量描述子系统之间的关联，因此本文基于FMEA方法，利用BN来实现石化动设备故障概率的定量风险评估。

BN是一种由节点、有向边和条件概率表(CPT)组成的概率推算工具。根据有无父节点，可将节点分为根节点、叶节点和中间节点。有向边由父节点指向子节点。节点和有向边共同组成网络，表示风险事件之间的因果关系，而CPT则用0～1之间的概率数将这种因果关系量化。传统的BN中节点呈现单态，并且根节点的边缘概率值具有确定性，这大大影响了评估结果的准确性。国内外学者考虑了BN中节点的多态性，并利用模糊数学相关领域知识考虑了根节点故障概率的模糊性和不确定性，形成了多态模糊BN。

1. 2 模型构建

基于FMEA和多态模糊BN的模型构建主要分为3个主要步骤：FMEA分析、FMEA分析结果与BN的转化、多态模糊BN的构建。FMEA分析可识别研究对象所有可能发生的故障模式，利用FMEA分析结果向BN转化可实现动设备的定量风险评估。但传统的BN中，各节点通常包含“正常”和“故障”两种状态，并且根节点的边缘概率通常为一个清晰概率值。为了提高评估模型的准确性，通过将传统的BN转化为多态模糊BN以改进上述缺陷。

1.2.1 FMEA分析

FMEA分析首先要明确评价对象边界，并将动设备划分为不同的独立子系统；其次要明确各独立子系统包含的零部件，零部件不重复包含在多个子系统中；再次根据设备台账记录情况分析不同零部件的故障模式，以及可能发生的潜在故障模式；最后分析不同故障模式可能产生的故障影响，其中故障影响包括对自身的影响和对其他零部件或子系统的影响。FMEA分析表见表1。

表1 FMEA分析表

1.2.2 FMEA分析结果与BN的转化

FMEA分析结果中包含子系统名称、故障部位、故障模式和故障影响，利用子系统、故障部位、故障模式之间的隶属关系，可转化得到BN的中间节点和根节点。故障影响结果中，利用对其他部位的影响可建立不同子系统中节点与节点之间的关联。FMEA与BN的转化关系见图1。

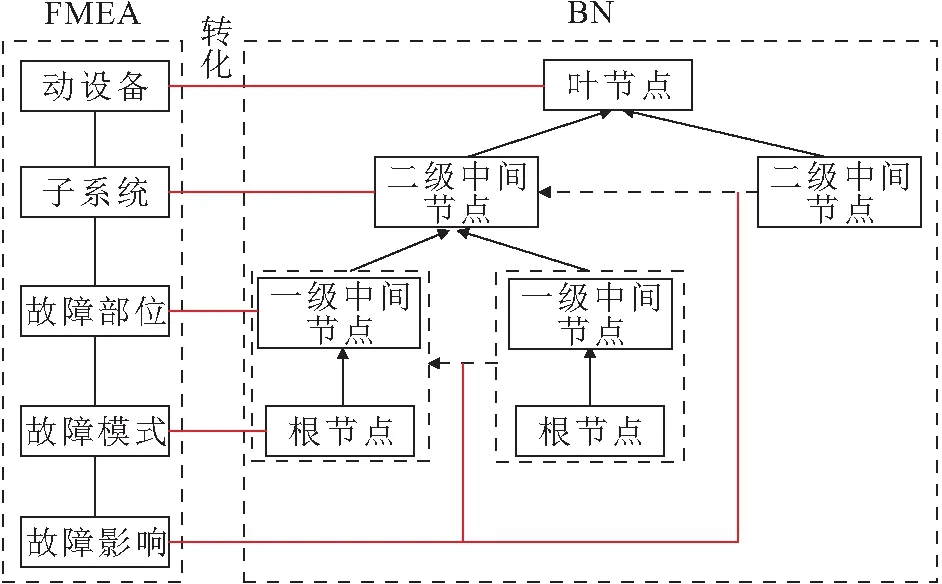
图1 FMEA与BN的转化关系Fig.1 Relationship between FMEA and BN

1.2.3 多态模糊BN的构建

在上述传统BN的基础上，通过以下节点状态和故障概率模糊子集的设置，可将传统BN转化为多态模糊BN。

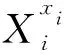
实际情况中，有部分零部件或子系统发生故障时，不会立即导致该部位停机，因此这部分零部件或子系统不只存在“正常”和“故障”两种状态。将上述情况的节点设置为“正常”、“半故障”和“完全故障”3种状态。

(2) 节点故障概率表示：为了替代清晰概率值，采用三角形隶属函数表示的模糊概率子集来描述各节点的故障概率。因此，各节点的故障概率模糊子集表示为{

P

,

P

,

P

}。其中，

P

为模糊子集的中心值；

P

、

P

分别为模糊子集的上、下限；

P

-

P

和

P

-

P

分别为左、右模糊区，代表模糊子集模糊程度的大小。由于我国尚无动设备的失效数据库，现实中往往难以确定故障概率模糊子集的上、下限，因此可用区间值表示模糊子集的上、下限，例如根节点

X

在故障状态

x

的概率子集表示如下：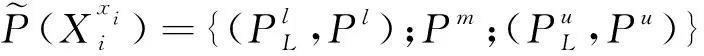

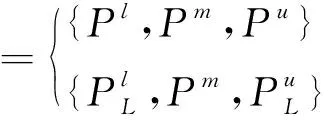
(1)

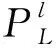
(3) CPT的设置：利用专家知识及实际经验设置CPT，从而可表达传统失效概率计算方法无法表示的风险事件之间的不确定性逻辑关系。CPT可表示某节点不同状态时，导致另一节点各状态分别发生的贡献值。因此，通过改变CPT中的条件概率可以实现系统故障机理变化的表征。但传统方法需要专家给出确定的概率值，难度较大且准确性难以保证。因此，本文利用模糊层次分析法(FAHP)来弥补传统方法的缺陷。

假设某父节点

X

有2个故障状态

x

、

x

，与其相连的子节点

Y

有3个故障状态为

y

、

y

、

y

。若要求父节点

X

在状态

x

下，子节点

Y

各状态发生的概率，即

P

(

Y

|

X

)，需专家基于表2中模糊语言回答问题“当节点

X

在状态

x

时，子节点

Y

的状态

y

和

y

谁更容易发生”，从而构造比较矩阵：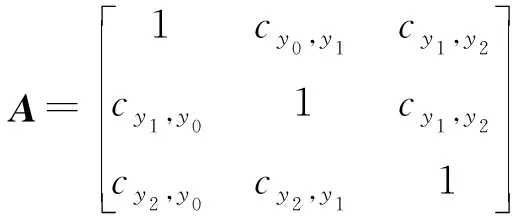

(2)

式中:

c

,=(

l

,

m

,

u

)表示与

y

状态相比，

y

状态发生的可能性大小。

表2 模糊层次分析法(FAHP)中的模糊等级

通过下式进行模糊加法运算：

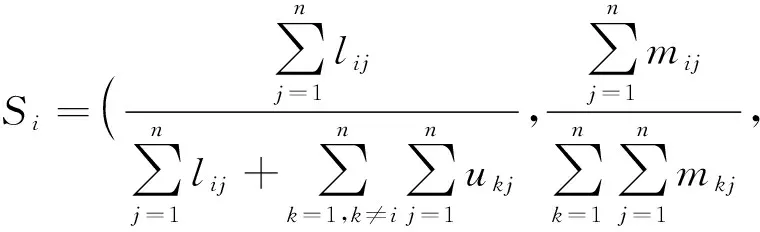
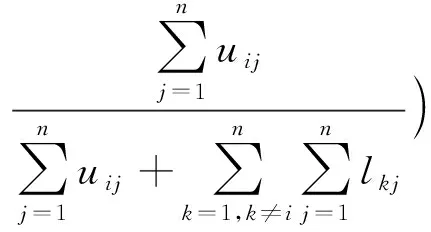
(3)

若上述比较矩阵通过一致性检验，则

Y

子节点在各个状态下的模糊向量可表示为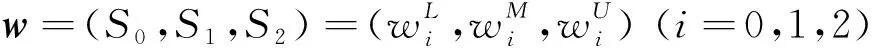

(4)

若比较矩阵无法通过一致性检验，则利用下面改进的模糊对数算法模型[见式(5)]可求解出模糊权向量: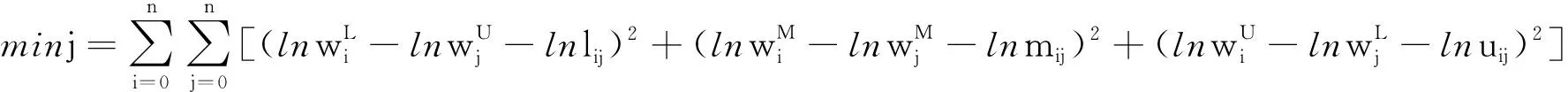

(5)

将上述模糊权向量解模糊化，最终可得到

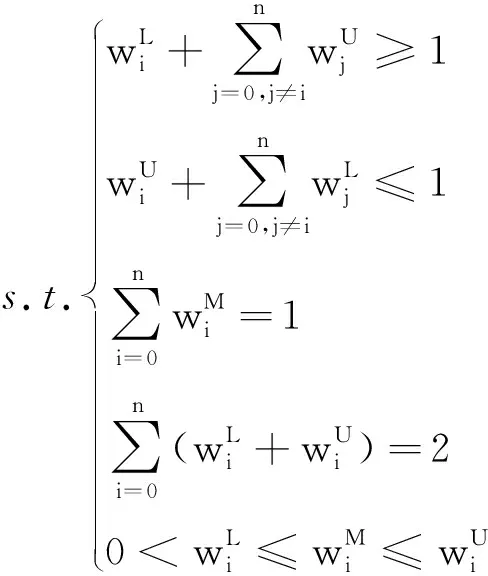
P

(

Y

|

X

)各值：

(6)

将上述结果扩展为父节点的多个状态，例如父节点

X

在状态

x

、

x

下子节点

Y

各状态发生的概率，计算方法如下：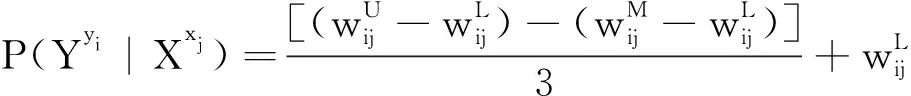

(

j

=1,2)

(7)

对于有多个父节点的子节点，例如

X

、

X

节点作为子节点

Y

的父节点，则无法判断

X

、

X

共同作用下子节点

Y

发生的概率，则利用下面分解法进行简化：

P

(

Y

|

X

,

X

)=

αP

(

Y

|

X

)

P

(

Y

|

X

)

(8)

若子节点

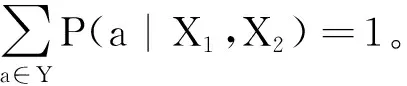
Y

有父节点

X

，

X

,…,

X

，而父节点

X

有

s

个状态，则公式(8)可扩展为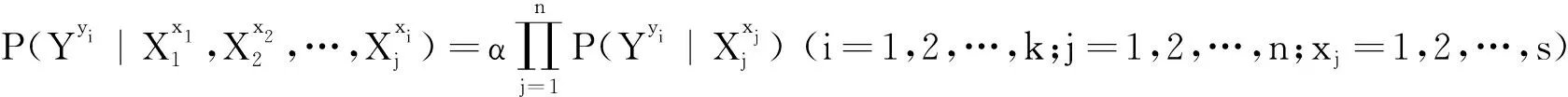

(9)

2 石化动设备故障概率定量风险评估模型求解

2. 1 动设备的故障概率模糊子集

假设根节点各故障状态下的故障概率模糊子集已知，则利用BN推理，可计算得到叶节点

T

在故障状态

T

下的故障概率模糊子集为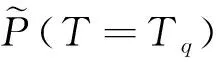

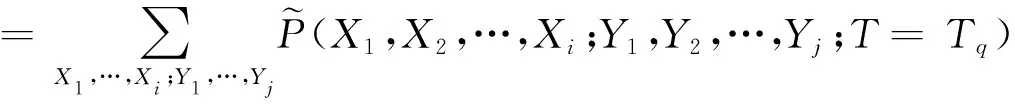
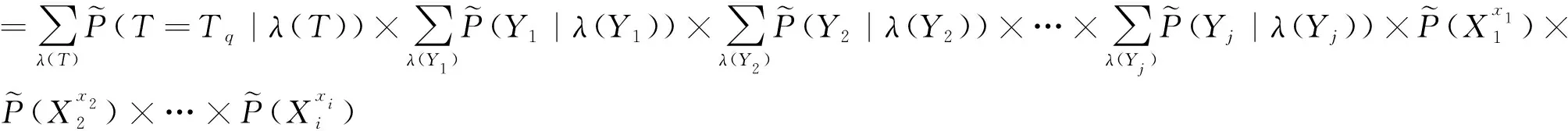
(10)

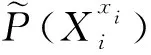
专家通过现场数据得到各零部件(根节点)的故障概率子集，再结合条件概率表中各部件对子系统、各子系统对动设备故障的权重值大小，代入公式(10)可得到动设备(叶节点)的故障概率模糊子集。

2. 2 零部件故障的后验概率

BN不仅可以正向推理得到叶节点的故障概率模糊子集，还可以利用反向推理计算根节点的后验概率，即为零部件故障的后验概率。该值表示动设备故障概率结果修正了的零部件各故障状态的故障概率，为现场零部件检修或更换提供指导依据。

由于利用公式(10)计算出的叶节点故障概率为模糊子集形式，因此可通过质心去模糊方法将故障概率的模糊子集转化为一个清晰概率值，再利用下式计算根节点不同故障状态下的后验概率：

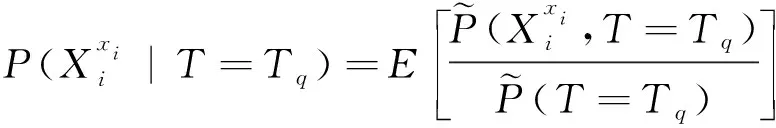
(11)

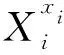
3 实例应用分析

本文应用上述构建的石化行业动设备定量风险评估方法，以现场某类型往复式压缩机为例，通过收集现场资料，主要包括该类型往复式压缩机技术档案、运行记录表、设备故障及检修记录，对其进行了定量风险评估。

3.1 往复式压缩机的FMEA分析

将该类型往复式压缩机划分为吸排气系统、传动系统、润滑冷却系统、填料密封系统和辅助系统，再利用FMEA方法对该类型往复式压缩机常见的故障模式进行分析，并通过故障影响的分析，发现气阀、气缸与活塞之间以及润滑冷却系统与吸排气系统、填料密封系统之间的关联，其FMEA分析结果见表3。

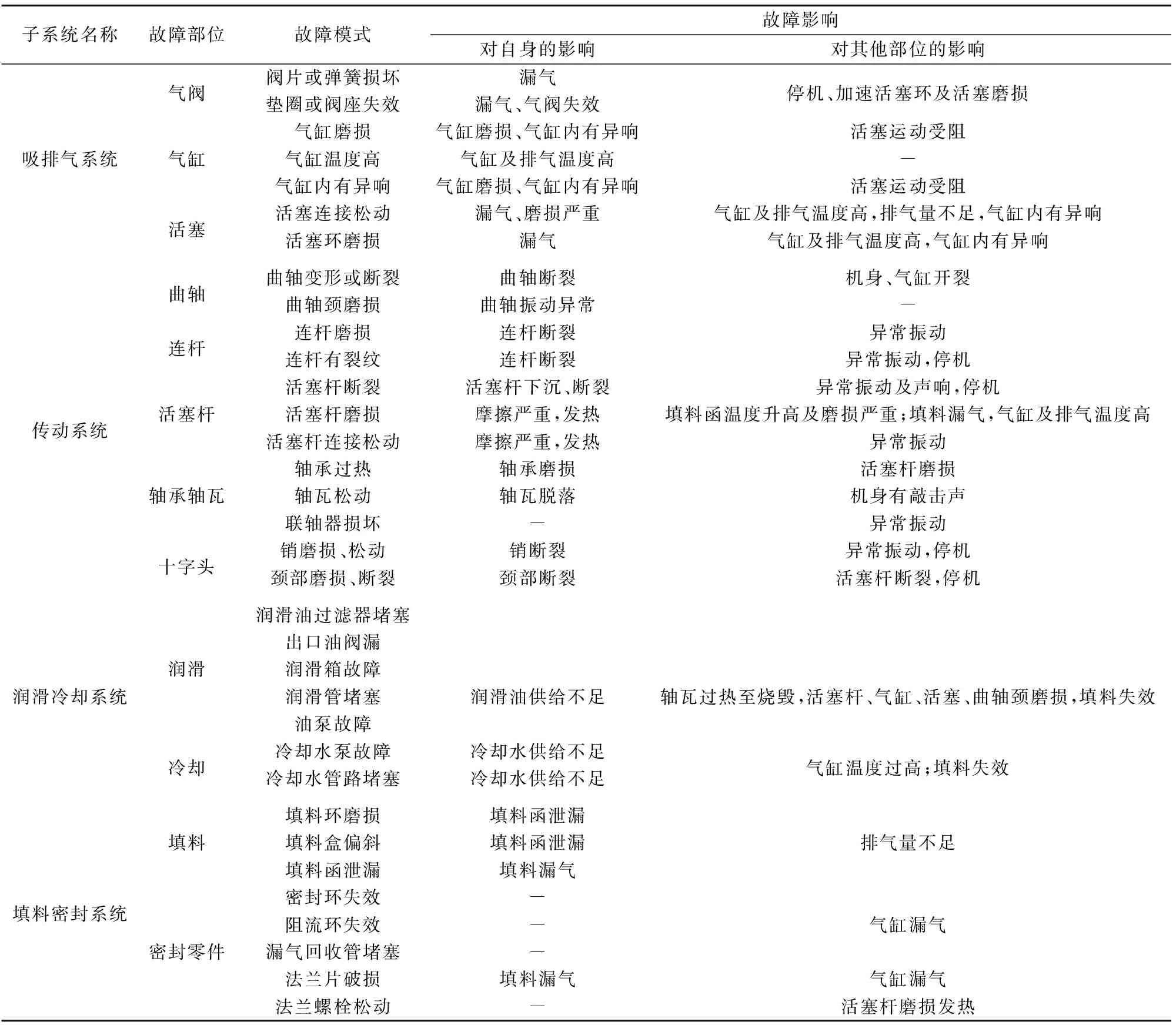
表3 某类型往复式压缩机的FMEA分析结果

3.2 构建多态模糊BN

根据图1和上述分析结果构建BN，最终得到的往复式压缩机风险评估BN模型见图2。由于阀片损坏、气缸磨损等故障模式有着明显的故障发展过程，故障模式的发展初期和后期对设备有着不同程度的影响，例如气缸磨损的初期可能会使气缸内有焊渣，导致活塞组件磨损加速，但后期的气缸磨损可能导致设备停机等严重影响。同时,故障部位

Y

～

Y

节点不同故障程度的影响不可忽略，因此将节点

X

、

X

、

X

、

X

、

X

、

X

、

T

以及

Y

～

Y

设置为多态，其故障状态包括正常、半故障、完全故障3种状态，分别表示为模糊数0、0.5、1，其余节点故障状态为0、1，分别代表正常、完全故障两种状态。根据现场历史数据，结合专家经验，可得到各根节点故障状态为1时的故障概率模糊子集(见表4)，并假设根节点故障状态为0.5时的故障概率模糊子集与根节点故障状态为1时的相同。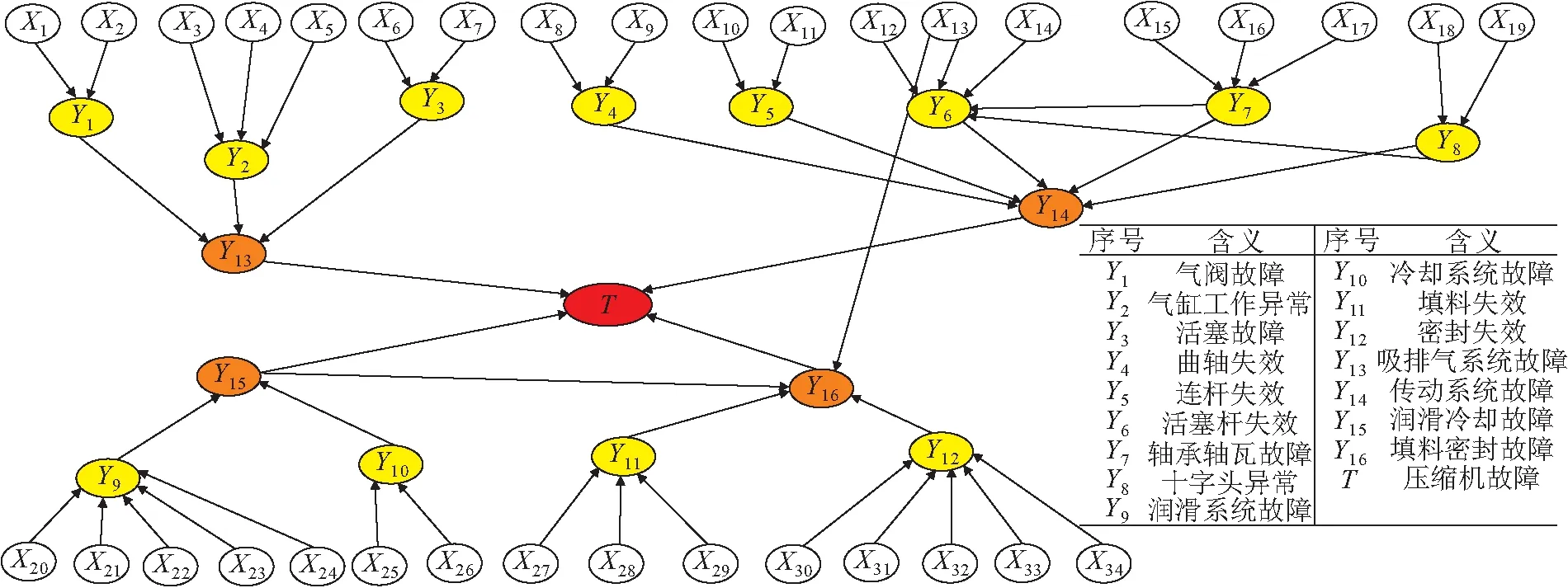

图2 往复式压缩机风险评估BN模型Fig.2 Risk assessment model of the reciprocating compressor

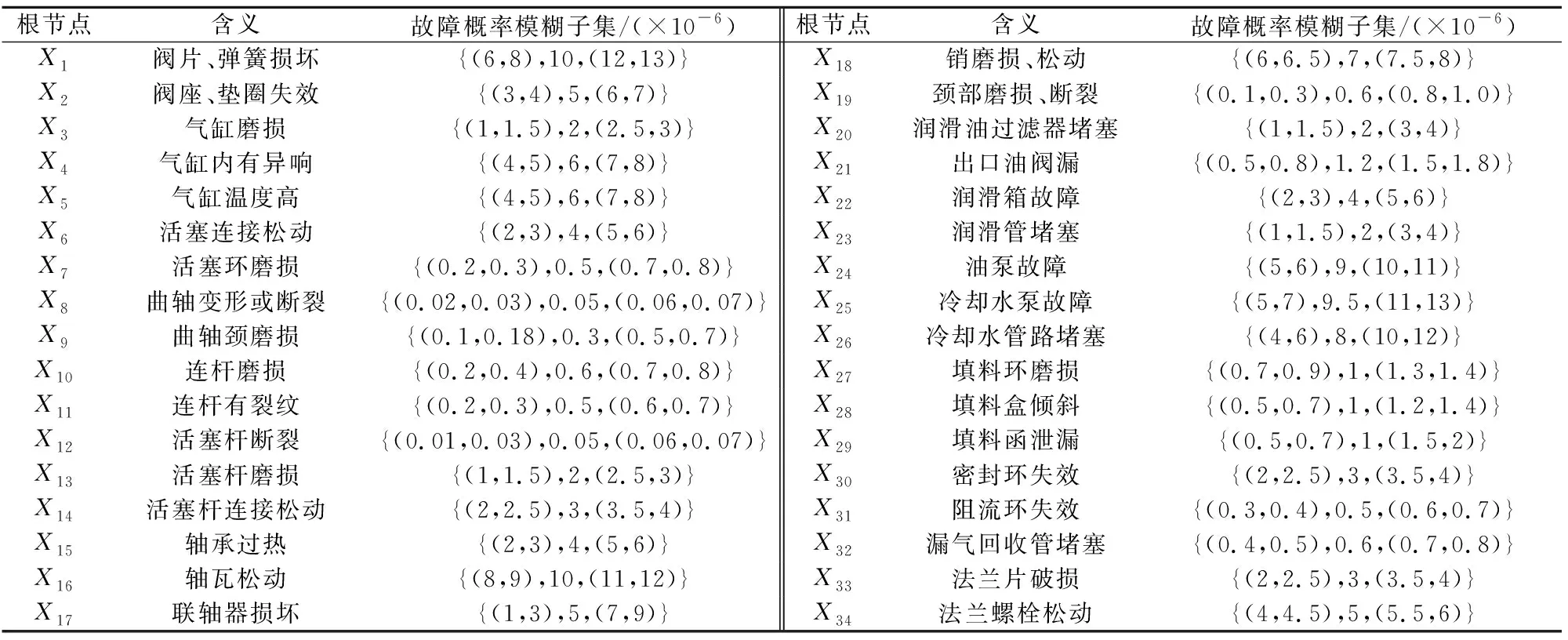
表4 根节点含义和故障概率模糊子集

由于实际生产时各部件间的故障关联性往往具有不确定性，通过第1.2.3节内容判断节点各状态之间的关系。因文章篇幅的限制，表5仅列出了

Y

节点的CPT，其余节点的CPT同理可得到。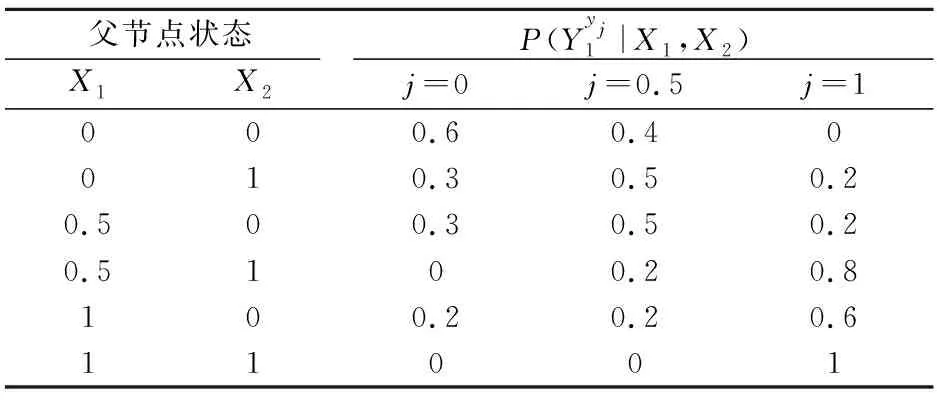

表5 Y1节点的CPT

3.3 计算多态模糊BN

基于图2的评估模型和公式(10)，可得到叶节点各故障状态下的故障概率模糊子集。但在实际生产中，

Y

～

Y

等中间节点的故障概率同样具有指导作用。通过公式(10)，可得到各中间节点的故障概率模糊子集的详细计算公式。例如中间节点

Y

的故障状态为1时，其故障概率模糊子集的计算公式为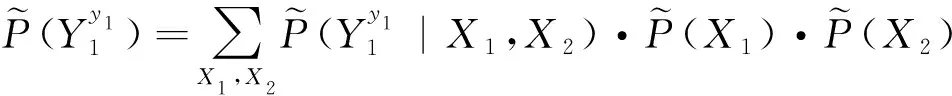

(12)

代入上述根节点的故障概率模糊子集和各节点CPT，利用模糊子集计算法则，可得到节点

Y

～

Y

和

T

各故障状态下的故障概率模糊子集，见表6。由表6可知，该类型往复式压缩机气阀(

Y

)和气缸(

Y

)出现半故障的概率较大，分别为0.004 0和0.004 5。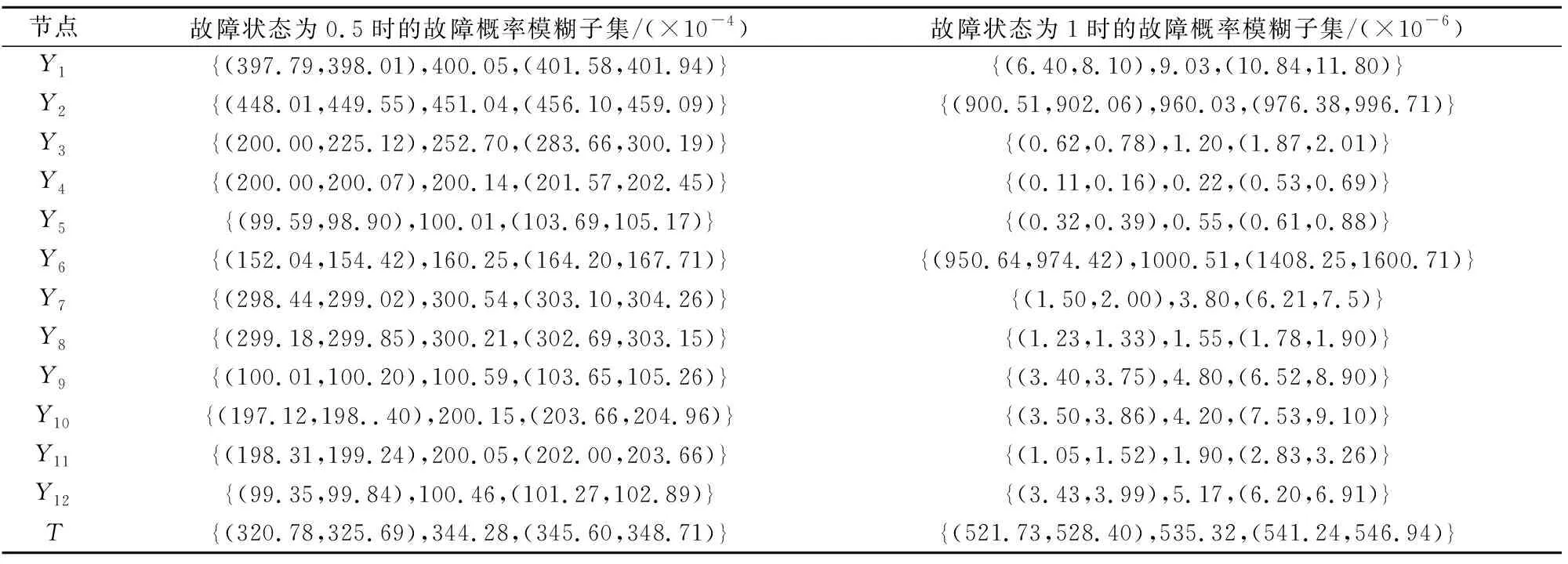

表6 Y1～Y12及T的故障概率模糊子集

在上述计算结果的基础上，利用BN反向推理的能力，应用公式(11)和质心去模糊方法，可分别得到叶节点故障状态分别为0.5和1时，各根节点不同故障状态下的后验概率，表7和表8分别给出了二态和多态根节点的后验概率计算结果。根节点的后验概率可用于该类型设备的故障诊断，可按照其后验概率的大小排序依次进行故障排查。

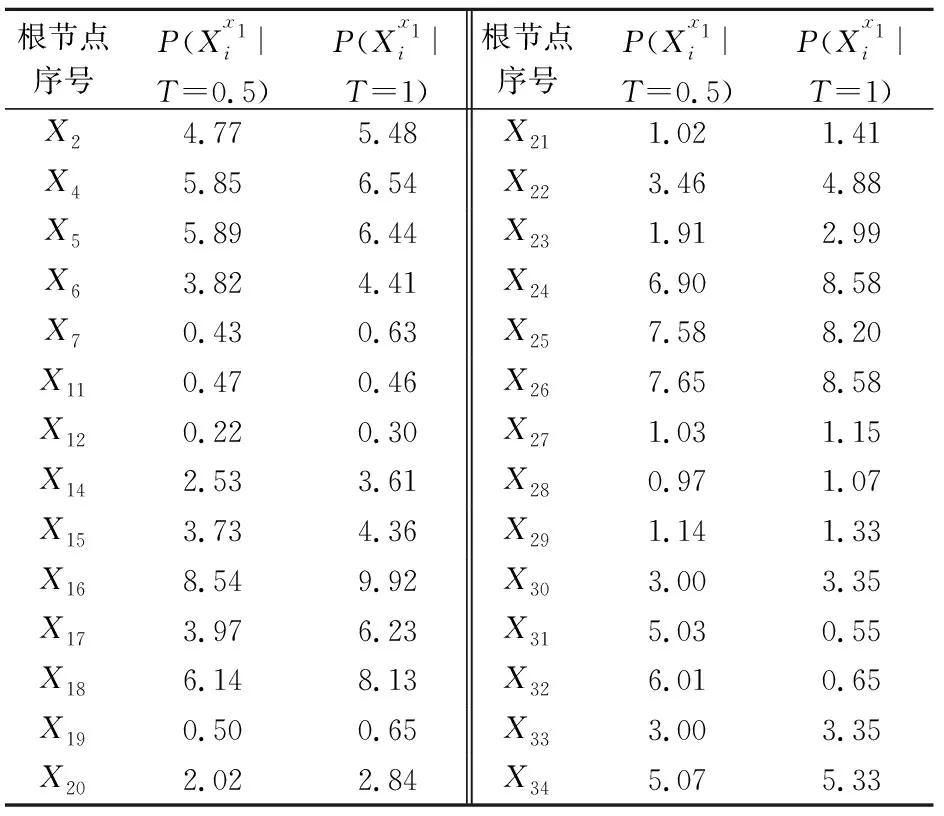
表7 二态根节点的后验概率(×10-6)

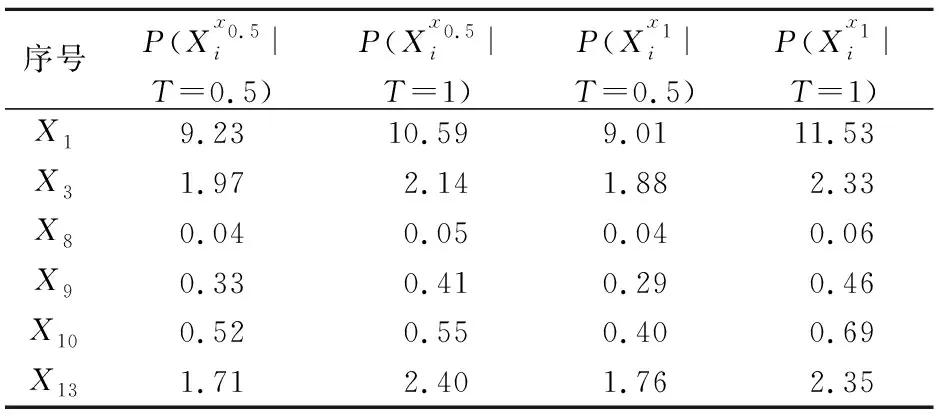
表8 多态根节点的后验概率(×10-6)

综合上述结果来看，该类型压缩机出现故障时，

X

(阀片或弹簧损坏)和

X

(轴瓦松动)的可能性较大，其后验概率分别为1.15×10和9.92×10。

4 结 论

(1) 本文分别利用FMEA和BN可实现故障模式识别和定量风险评估的特点，基于FMEA分析结果中风险事件的因果关系，结合FMEA方法和BN建立了石化动设备的定量风险评估模型。

(2) 考虑实际情况中零部件故障呈现多态性和压缩机现场数据匮乏，将节点设置为多态，同时将根节点边缘清晰概率值替换为概率模糊子集，并利用模糊层次分析法构建了条件概率，最终实现传统的BN向多态模糊BN的转换，提高了评估模型与实际情况的贴合度。

(3) 将上述风险评估方法应用于现场某往复式压缩机的风险评估中，利用FMEA方法分析了其可能发生的故障模式和影响，并基于FMEA分析结果，通过多态模糊BN的正向推理能力，计算了动设备及子系统的故障概率，其中气阀和气缸出现半故障的概率较大，分别为0.004 0和0.004 5，符合实际情况；同时，利用BN的反向推理能力，计算得到零部件故障的后验概率，可用于指导该类型往复式压缩机的故障诊断。