高温空调系统性能仿真与分析

周永戬，赵康佐，胡海涛*，袁修海

（1-上海交通大学制冷与低温研究所，上海 200240；2-上海海立特种制冷设备有限公司，上海 200090）

[关键字] 高温空调；稳态仿真；模型

0 引言

高温空调器指应用环境温度较为特殊的一类空调器，其工作环境温度一般在50～80 ℃[1-2]。20世纪80年代，高温空调器随着冶金项目的引进开始在我国普及；钢铁冶金车间内的行车随位置变化，环境温度变化十分剧烈，必须使用高温空调器满足驾驶人员的热舒适性要求[3]。目前，针对高温空调的设计资料较少，尚没有全面规范的设计方法[4]。

目前针对高温空调的研究主要集中于替代制冷剂的选择与实验研究[5]。由于特殊的工作环境，一般的制冷工质很难满足要求[6-7]。目前高温特种空调机使用的制冷剂主要为R142b，该工质化学性质稳定、无毒无臭，但R142b属于HCFC类工质，在《蒙特利尔议定书》的规定中，属于加速淘汰类制冷剂[8]。R134a有良好的综合性能，作为R12（CFC类工质）的主要替代物在高温空调上的使用有逐渐增多的趋势，但由于在高温下使用时，会导致冷凝器冷凝压力过高，所以主要用于不高于65 ℃的环境温度[9-10]。此外，高温空调器的理论分析只能简单计算系统能效等参数，无法反映部件间的耦合关系与对空调系统的影响，难以指导系统优化设计[11]。而实验研究由于成本及控制问题，通常只进行系统性能与制冷工质组分的关系研究，也无法反映部件对系统性能的影响[12]。

本文选取R236fa作为制冷剂，开发了高温空调系统稳态仿真模型，通过建立各部件的仿真模型与耦合关系，构建能够反映高温空调特点的系统模型，指导高温系统的设计与优化，并进行对比分析。

1 仿真模型

高温空调机由压缩机、冷凝器、蒸发器和膨胀阀组成。系统运行时，制冷剂气体经由压缩机绝热压缩后进入冷凝器进行等压放热，然后进入膨胀阀进行节流降压，最后通过蒸发器吸收热量重新变为低压气体[13]。

1.1 制冷剂选择

将高温空调系统常用的工质及本文使用的R236fa的物性参数进行整理[14-16]，如表1所示。

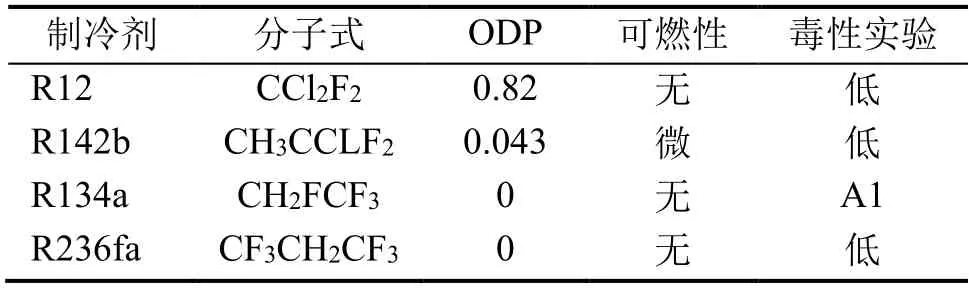
表1 常用制冷剂参数比较

由表1可知，R12作为CFC类制冷剂，对环境破坏严重，且有一定毒性，已被淘汰使用；R142b安全性较差，并且属于HCFC类制冷剂，对环境危害较大，目前处于加速淘汰的阶段。当冷凝温度达到80 ℃时，R134a的饱和压力达到2.6 MPa，超过工程上的冷凝压力上限（2.5 MPa），对压缩机及配套设备提出了更高的要求，并且功耗量也有一定的增加。而R236fa作为一种环保型制冷剂，具有热稳定性好、沸点高、临界压力高和临界温度高等良好的物理性质，且无毒无腐蚀性、不燃不爆且安全性好，故本文中采用R236fa作为高温空调系统的制冷剂。

1.2 压缩机模型

压缩机模型需要根据初始值或蒸发器的输出参数计算压缩机质量流量、输入功率和排气温度[17]。目前应用于高温空调的主流压缩机为涡旋式压缩机，这种压缩机没有吸、排气阀，工作可靠、寿命长，且由于不存在余隙容积，故在较大的压比范围内都具有较高的容积效率。为提高模型的适应性，简化模型复杂度，采用结合产品实验数据和理论模型的方法。通过理论模型保证适用大部分工况，通过产品实验数据拟合理论模型中的部分参数可以简化模型并提升模型对产品的仿真精度。

根据已有的压缩机近似拟合模型[18]，给定频率f，质量流量的计算公式为：

综合学者文献所述，产业转移对区域经济和乡村振兴的影响是不确定的，需要进一步验证。回归式产业转移作为新的产业转移模式，在推动落后欠发达地区经济发展究竟起着怎样的作用，也需要通过实证进一步验证。本文就是基于此，通过数据实证分析，在制度资本的参与下，考量和探究回归式产业转移推动区域经济增长背后的动力和逻辑机理。

式中，m为质量流量，kg/s；V为压缩机气缸容积，m3/rev；f为频率，Hz；v为吸气比容，m3/kg；p为压力，kPa；a、b为拟合系数；下标e为蒸发器；下标c为冷凝器。

当给定任意频率fx时，可根据频率插值进行计算，通用近似模型为：

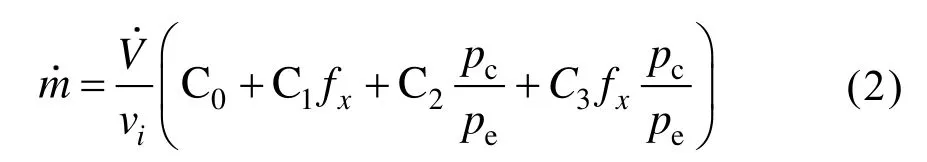
式中，C0～C3为与频率无关的拟合系数。

压缩机功率的计算可采用如下的拟合形式：

式中，c为电机的摩擦功率，W；d为指示效率；n为多变指数；下标th为理论值。

将压缩机看作单结点，则集中温度Tcom即为排气温度Td。由能量平衡方程有：

式中，Q1为压缩机壳体与近壳体环境Tar之间的换热，W；Q2为内部生成热，W；Dh为压缩机的当量球体直径，m；α为压缩机壳体与近壳体环境的换热系数，W/(m2·K)；ε为压缩机壳体的黑度；σ为玻尔兹曼常数；下标in为进口；下标out为出口。

1.3 换热器模型

制冷剂侧和空气侧控制方程：

能量平衡方程和动量方程：

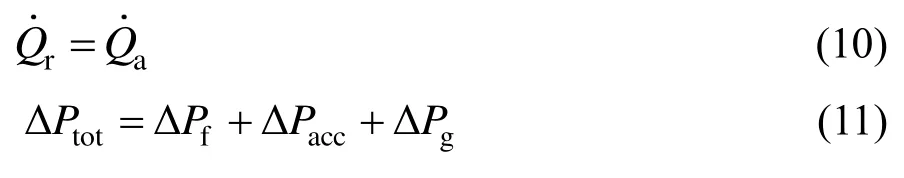
制冷剂质量计算公式：

式中，k为传热系数，W/(m2·K)；F为传热面积，m2；h为焓值，J/kg；L为相区长度，m；ρ为制冷剂密度，kg/m3；A为横截面积，m2；dK为制冷剂侧与空气侧传热面积之比；ΔT为换热温差，K；C为截面周长，m；下标i为相区编号（1为过热段、2为两相段、3为过冷段）；下标i为相区编号（SH为过热段，TP为两相段，SC为过冷段）；下标r为制冷剂侧；下标a为空气侧；下标w为壁面。

1.4 膨胀阀模型

由于在行车移动中，高温空调使用场合环境温度变化大，故节流元件使用膨胀阀。膨胀阀中的制冷剂被迅速降压，可将其看作绝热等焓节流过程：

流量特性可以采用式(15)计算：

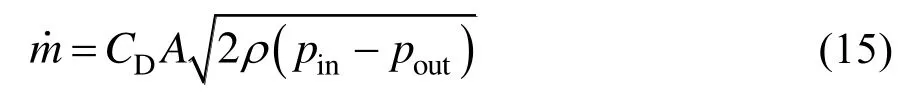
式中，CD为流量系数。

2 模型精度验证

2.1 压缩机模型精度验证

将压缩机模型与实验数据进行精度验证，如图1所示。实验压缩机额定频率为60 Hz，测试频率范围为45～90 Hz。验证结果表明，该压缩机模型对流量的计算误差在±5%以内，最大误差为4.9%，平均误差为2.0%。

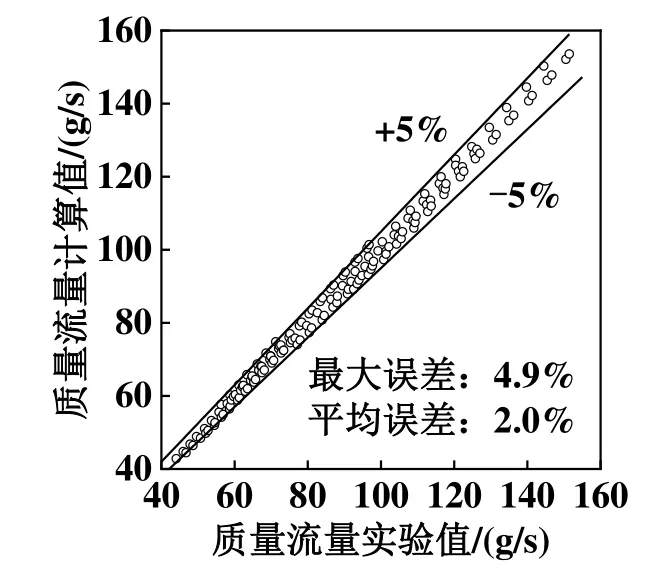
图1 压缩机模型精度验证

2.2 换热器模型精度验证

将换热器模型与实验数据进行精度验证，如图2所示。实验工况包括25个冷凝工况点，18个蒸发工况点。验证结果表明，该换热器模型对于冷凝工况的换热量计算误差在±5%以内，最大误差为4.3%，平均误差为1.4%；该换热器对于蒸发工况的换热量计算误差在±5%以内，最大误差为-4.8%，平均误差为2.4%。

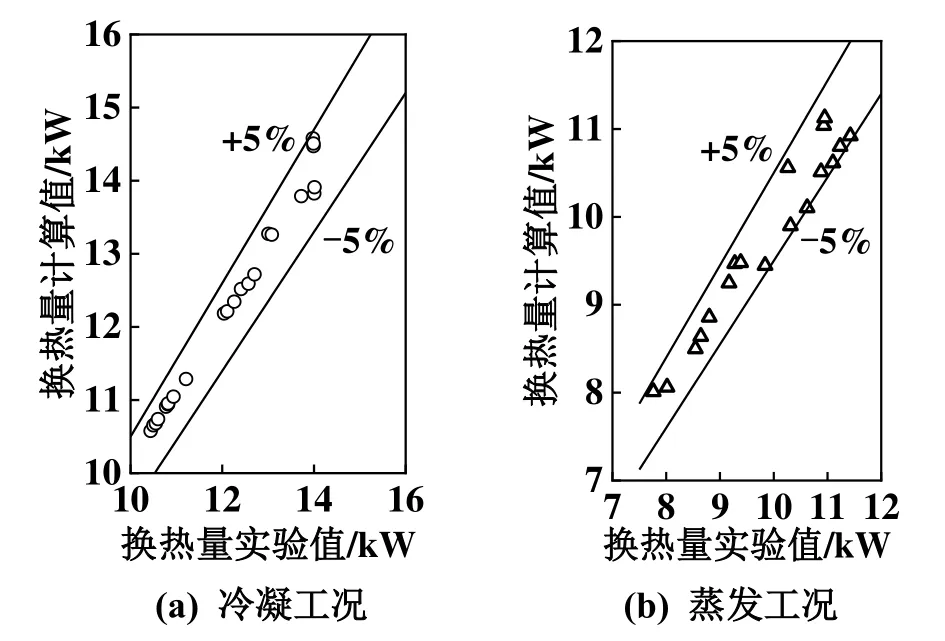
图2 换热器模型精度验证

3 系统求解算法

对于高温空调的系统仿真，本文采用基于质量引导的求解算法，如图3所示。以各部件中的制冷剂质量为迭代判据，首先分别判断高压侧及低压侧制冷剂充注量是否等于预测值，再判断膨胀阀与压缩机的质量流量是否相同；当系统中各位置质量流量相同，且高低压侧制冷剂充注量达到稳定时，系统达到稳定运行状态。

图3 高温空调系统求解算法流程

具体步骤如下：1）系统初始化，即假定部分参数如冷凝压力、蒸发压力等，计算其他参数；2）计算此工况下膨胀阀中制冷剂质量流量；3）判断此工况冷凝压力是否满足最大值与最小值要求，若是，则转入步骤4，否则跳出循环，转入步骤6）；4）计算此工况冷凝器中含有的制冷剂质量；5）判断高压侧（冷凝器与压缩机）制冷剂质量计算值是否为假定值，若是，转入步骤6，否则调整冷凝压力，转入步骤3；6）判断此工况蒸发压力是否满足最大值与最小值要求，若是，转入步骤7，否则跳出循环，转入步骤9；7）计算此工况蒸发器中含有的制冷剂质量；8）判断低压侧（蒸发器）制冷剂质量计算值是否为假定值，若是，转入步骤9，否则调整冷凝压力，转入步骤6；9）计算此工况下压缩机中制冷剂质量流量；10）判断压缩机中制冷剂质量流量是否等于膨胀阀中制冷剂质量流量，若是，输出结果，否则调整高压侧、低压侧制冷剂质量，转入步骤2。

4 结果与讨论

4.1 制冷剂充注量的影响分析

图4分析了系统能效比（Energy Efficiency Ratio，EER）及系统制冷量随制冷剂充注量变化的情况。图中的工况为高温空调常用工况，蒸发温度10 ℃、室外温度60 ℃[5,10]。

图4 系统能效/制冷量随制冷剂充注量的变化

由图4可知，随着制冷剂充注量的增加，系统能效比和制冷量都呈先增加后减少的趋势；在充注量为320 g时，系统能效比达到最大值1.29，系统制冷量达到最大值4.02 kW。这是因为系统存在最优充注量，当接近最优充注量时，系统制冷量的增加较快，而系统能耗增加较慢，故能效比呈上升趋势；当超过最优充注量后，系统能耗增加较快，而制冷量增加较慢，故能效比呈下降趋势。

4.2 R236fa和R134a、R22/R142b系统性能分析

压缩机排气温度随室外温度的变化趋势如图5所示。压缩比随室外温度的变化趋势如图6所示。

由图5可知，随着室外温度的上升，压缩机排气温度逐渐上升，但是应用R134a的制冷系统压缩机排气温度增量明显大于应用R236fa的制冷系统。随着室外温度从35 ℃增加到60 ℃，两者的差值从1.6 ℃增加到3.8 ℃。

图5 压缩机排气温度随室外温度的变化

由图6可知，R236fa系统压缩比高于R134a系统，且随室外温度的升高，增加幅度逐渐提高。随着室外温度从35 ℃增加到60 ℃，R236fa系统相较于R134a系统平均增加13.8%。

图6 系统压缩比随室外温度的变化

系统EER随室外温度的变化趋势如图7所示。R236fa制冷系统EER高于R134a系统。随着室外温度从35 ℃增加到60 ℃，R236fa系统EER逐渐降低。随着室外温度提高，与R134a系统相比，R236fa系统EER增大程度逐渐提高，最大增加14.7%；与R22/R142b混合制冷剂系统[5]相比，R236fa系统EER最大提高13.4%。

图7 系统EER随室外温度的变化

5 结论

本文建立了适用于高温空调系统的稳态仿真模型，并对比分析了R236fa、R134a和R22/R142b混合制冷剂系统性能。研究结果表明：随着室外温度由35 ℃增大到60 ℃，R236fa系统EER逐渐降低，且比R134a系统EER的增大程度逐渐提高，最大增加14.7%；R236fa系统EER比R22/R142b系统最大提高13.4%。