配合对中小车的船舶总段智能对接解算策略

吴俊生，伍朝晖,褚超平,房 建,张伟军

(1.上海交通大学机械与动力工程学院，上海 200240;2.江南造船(集团)有限责任公司，上海 201913)

0 引言

现代造船模式以分段制造工艺方法为主，是在引进焊接技术后以钢制船舶建造技术为基础而建立的建造方法[1]。按照建造单元的大小划分，大型船舶的建造方法分别为:一般分段建造法、环形总段建造法和巨型总段建造法。

造船现代化于21世纪初启动，为了提升造船的速度和效率，强势造船公司实践了总段巨型化，并向异地并行、无缝整合的方向奋进。由于造船向量化、绿色化、信息化和全球化发展，将使造船资源、能源和金融产生结构性的变革[2-5]。

传统的塔式建造方式已经在逐步改变，吊装模式变换的驱动仅仅是吊装总重的增加，本质上是对附属设置的更新进而提高船坞的利用率。使用吊装设备进行船段的合拢和建造仍然有许多问题[6]。

目前，国内的一些大型船厂引入了新设备进行总段的合拢对接工作。江南造船集团使用的是一种承重重量达到 200 t 的轨道对中小车。该小车具有X(轨道方向)、Y(垂直轨道方向)、Z(重力方向)3个方向的移动调整能力，可以多台对中小车组合协同完成总段的合拢对接工作。实际作业时，不再使用吊车吊拉总段，而是使用若干辆对中小车自总段底部顶升总段进行总段合拢工作。吊车在总段对接作业中仅起到初步模拟搭载定位的工作。

本文以这种对中小车为基础，以总段智能对接为目标，提出了从测量系统到对中小车阵列的控制量计算方法。改变了总段对接的人为控制和经验判断的模式，提高了总段对接的精度、效率和信息化程度。

1 总段智能对接系统

总段智能对接系统采用多个离散分布的相对位置灵活可变的对中小车,通过对接特征点自动测量、对中小车自动定位和对接数据自动解算技术，结合对接工艺要求及对接总段的结构变形，自动生成对中小车阵列的协同控制位置/力指令，优化多对接特征，实现总段高精度对接。系统之间的关系如图1所示。

图1 总段智能对接系统

图1中，小车定位系统采用激光测距仪自动寻的技术，可自主搜索周边小车的位置，并通过激光跟踪仪对某台小车标定位置后纳入特征点自动测量系统；特征点自动测量系统兼容iGPS(室内GPS)和激光跟踪仪，可以对总段侧面及端面的特征点进行自动跟踪和测量；对接数据解算系统完成小车的初始状态优化、变形检测与控制、对接目标优化计算以及刚体变换控制，输出小车阵列的目标位置；小车协调控制系统通过选择设定小车各轴运动，采用位置伺服环和压力伺服环控制，可最终协调控制各小车达到目标位置。

对接数据解算系统根据对接逻辑步骤，可以划分为系统位姿与变形识别、位姿调整量求解方法2部分。

2 系统位姿与变形识别方法

控制系统中位姿与变形识别的数据来源，是测量系统提供的移动段实时监测点点云数据，以及对接目标提供的监测点和特征点点云数据。

在获取以上2种数据后，可以通过监测点与特征点的映射关系获取实时特征点点云的位置。并根据实时特征点和目标特征点2组点云的匹配关系，确定2组矩阵之间的最优齐次变换矩阵。该矩阵内包含的信息反馈了移动段的位姿状态。而在齐次变换后的点云匹配误差则反映了移动段的变形量。移动段的位姿与变形识别流程如图2所示。

图2 移动段变形与位姿识别逻辑

本解算方法中主要着手解决3个算法方面问题：统一测量场、剔除粗大误差和最佳点云匹配。

2.1 统一测量场

在实际计算时，仅有在同一坐标系下的数据互相才具有位姿判断条件。所以在进行位姿识别时，需要把所有数据都转换到统一的坐标系下。在本对接方案所遇到的实例中，主要是将对接目标中的数据和现场的实时数据统一到同一坐标系下进计算。

统一坐标系是依靠在现场实际布置3个实体测量点，假设这3个点分别为A,B,C。则3个点在测量设备坐标系(记作坐标系1)中的坐标为

(1)

以这3点作为统一测量场的基准，A点为统一测量场原点，AB连线为统一测量场X轴方向，AB、AC叉乘构成的向量为统一测量场Z轴方向，最后由统一测量场的Z、X轴叉乘出统一测量场的Z轴方向。将统一测量场坐标系记作坐标系O，即

(2)

这样就得到了统一测量坐标系上的3个坐标轴基矢量在测量设备坐标系中的坐标。在平移原点到O点以后，2个坐标系之间存在1个旋转矩阵R，即

(3)

由式(3)可知，统一测量场3个基矢量在测量设备坐标轴中向量构成的3×3矩阵的转置，就是从测量设备坐标系到统一测量场的旋转矩阵。

同时，又因为原点平移到O点,故可知平移矢量S为：

S=-RTA

(4)

故可求得转到统一测量场的齐次变换矩阵为

(5)

利用该矩阵，就可以针对不同的测量设备进行测量场的统一化处理。

2.2 最佳点云匹配

最佳点云匹配是一种基于四元数法的点云配准算法，可对2幅点云图进行旋转及平移变换，从而使之达到最小二乘法意义上最佳重合状态。在总段对接系统中，由于仅布置有限个测量点，并且获取测量点的可以通过物理信号通道对测量点序号进行识别。所以实际上是对2组已经序号配准的点云求齐次变换的最小变换矩阵。使用四元数法可以得到一个最佳结果[7]。

设平移向量为T,B={Bi}为基准点云，M={Mi}为待匹配点云。点云匹配的目标即为

(6)

将2幅点云坐标相对重心进行平移，设重心坐标为uB,uM，即

(7)

构造协方差矩阵与特征矩阵，设协方差矩阵为M，特征矩阵为Q，即

(8)

(9)

计算出Q的最大特征值，将最大特征值的特征向量作为四元数qR。由qR构建旋转矩阵R，即

R=

(10)

并求出平移向量S为

S=uB-RuM

(11)

根据R、S构建齐次变换矩阵T为

(12)

该齐次变换矩阵T就是2组点云之间的变换矩阵。

2.3 剔除粗大误差

在点云匹配之前需要首先经过数据进行处理，剔除粗大误差，才能保证点云匹配算法的正确性。本算法按照逻辑顺序应该排在最佳点云匹配之前。但是实际上本算法中需要运用到最佳点云匹配的方法，所以将其放在最佳点云匹配之后。

粗大误差的来源可能是由于测量设备出错，也可能是通信中的干扰。在运用该算法之前需要首先遵循一个假设：相对于所有的测量点，测量传输出错的点始终在少数，即大多数测量点理论上应该是正确的。

剔除粗大误差点的算法逻辑如图3所示。

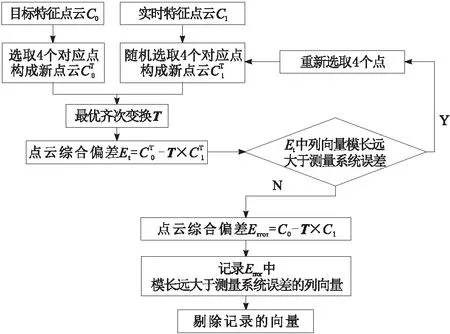
图3 粗大误差剔除逻辑

粗大误差的剔除本质上是对点云数据的预筛选。首先在点云中随机选取了4组对应点进行最优齐次变换矩阵的求解。之后求解2组选取的随机点云的匹配误差，若发现这种模长远大于测量误差的列向量数量较多，则说明选取的4个点中存在粗大误差点。由于假设中粗大误差点的数据是少数，所以重新选取点进行剔除即可。若选取的4个点中不存在粗大误差，则求解实时特征点云以该齐次变换矩阵进行矩阵变换后的数据，与目标特征点云的匹配误差。匹配误差中若存在模长远大于测量系统误差的列向量，则说明该列向量所对应的特征点就是测量的极大误差特征点。剔除这些点以后就可以进行特征点最佳匹配了。

算法中有关具体参数设置的细节如下所述。

a.随机选取点的个数是4个以上：尽管理论上3个点就可以确定1组点云的空间数据，但是3个点确定的点云数据存在手性上的对称问题。尽管在确定3个点各自以相同的序号和顺序排列以后可以排除手性问题，但是为了避免麻烦选取的点个数建议选择4个或者以上。同时,随机选取的点数应该尽可能少，这样在筛选的时候才能保证尽量不带入粗大误差点。因此，每次选取点时选取4组特征点。

b.Error模长误差的阈值：每4组不同的随机点计算出的模长误差都不相同。所以这里建议设置浮动阈值，阈值的选择遵循如下依据：测量系统误差除去4个随机选取点云的范围尺度乘上整体点云的范围尺度。

3 位姿调整量求解算法

位姿调整量求解的数据来源是测量系统提供的小车定位信息，以及在上一层逻辑中获得的移动段位姿。根据移动段位姿可以对调整策略进行分解，获得在绕Z、Y、X等3个轴上所需的调整量，通过这样的分解可以将三维调整信息降维为二维调整信息。根据该调整信息结合小车定位信息可以构建一个二维的旋转矩阵。对该旋转矩阵与小车定位信息中所获取的小车顶柱中心位置点云信息，经过综合计算可以获得1组新的小车目标位置点云。新点云与实测点云的位置偏差经过处理后即可成为下达的位姿调整量。求解位姿调整量的逻辑如图4所示。

图4 位姿调整量求解

本解算方法中主要着手解决2个算法方面问题：移动段位姿分解为绕Z、Y、X轴偏差；由小车目标位置信息到位姿调整量的转换。

3.1 移动段位姿分解

由位姿识别部分所得到的位姿本质上是一个齐次变换矩阵。若以该齐次变换矩阵矩阵直接与小车定位信息相乘求出小车目标位置。会发现调整量是一个三维方向的调整指令，这对于目前小车的结构设计难以实现。并且即使可以按照三维调整指令下达调整指令，也难以保证小车在运动过程中保持整体协调运动，而非协调运动必然导致调整效率低下和调整分布不均。

综上，在调整时需要对移动段位姿进行分解，将复杂的三维调整指令进行降维处理。在本方法中，将移动段位姿分解为绕Z、Y、X轴3周的调整量。

已知在位姿识别模块中获得的移动段当前状态的齐次变换矩阵为T，它所对应的旋转矩阵和平移矢量分别为R、S。

对移动段位姿分解其实就是将齐次变换矩阵中的旋转矩阵R，分解为绕Z、Y、X等3个轴旋转的矩阵相乘，即

R=RZ(α)RY(β)RX(γ)

(13)

这种分解方式同时也展示了位姿调整的策略。从逆序上看，移动段从目标位置移动到当前实时位置，需要依次绕统一测量场坐标系的X轴旋转γ、绕Y轴旋转β，以及绕Z轴旋转α这3个步骤。

由于旋转矩阵R已知，故可以从旋转矩阵中获取绕Z、Y、X轴的旋转角度：

(14)

根据式(14)完成了位姿的分解，同时根据该分解也确定了位姿调整的顺序：绕Z轴→绕Y轴→绕X轴。这一顺序也与当前人工对接思路相同。

3.2 由小车目标位置信息到位姿调整量的转换

在进行位姿分解以后，可以将调整量从三维信息降维到二维，但是末端的执行设备由于设计问题。每次只能同时移动主缸(重力方向)或副缸(水平方向)。这意味着在单次运动的时候仅能控制1个自由度(Z或Y)，无法同时使得移动段在不同自由度之间协同调整。这就存在小车目标位置信息到位姿调整量的转换问题。

3.2.1 调整对象分类

在这里，首先需要明确对Z、Y、X轴调整时实际的执行设备调整原理，即针对各个轴的调整到底需要调整对中小车的哪个方向的油缸。

调整Z轴：调整Z轴本质上是在对对中小车的副缸进行调整，其调整的控制范围较大，底部排布的小车支撑点构成的拟合平面与旋转轴接近垂直,所以可以近似为平面绕接近垂直向量的旋转。如图5所示。

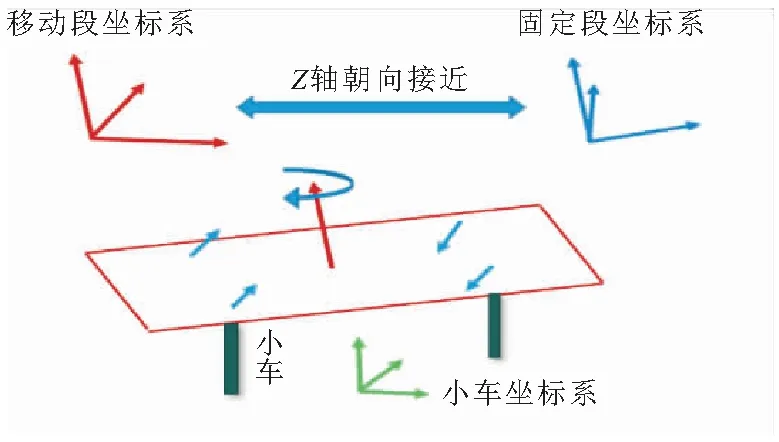
图5 调整Z轴

调整Y、X轴：调整X轴与调整Y轴本质上是相同的，都是对对中小车的主缸进行调整。相对于调整Z轴更为简单。因为底部排布的小车支撑点构成的拟合平面与旋转轴几乎平行，所以可以近似为线段的旋转。如图6所示。

图6 调整Y、X轴

3.2.2 主缸调整时调整量降维策略

首先针对调整Y、X轴这一相对较为简单的主缸调整，如图7所示。

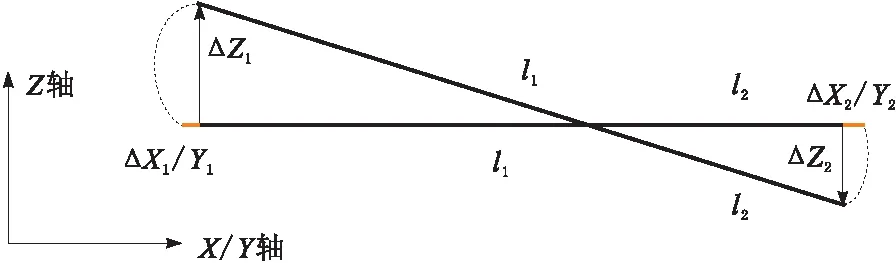
图7 主缸调整

可以看到在实际旋转中，对中小车想要达到目标需要同时在X方向上移动。这与执行系统单次仅能对1个自由度调整的要求相悖。因此，当前的执行系统是不能够完全满足调姿需求的。但是需要注意的是，实际上对中小车在运动时与顶升接触部分并非是完全绞死的。移动段与对中小车之间的连接部分，可以看作是一个可在一定平面范围内滑动的球铰，如图8所示。

图8 球窝模型

可以大约估算ΔX或ΔY的数量级：

(14)

可以发现，移动段在ΔX或ΔY上的移动量。相对于Z轴上运动量可以算是一阶小量(调整量相对于移动段尺度是一阶小量)。故移动段在次要方向的滑动可以被近似忽略，在实际运动中也会被球铰与球窝的相对滑动所兼容。所以在处理时仅需要向调整系统传递Z轴上的运动量即可。这就完成了从二维调整信息向一维调整信息的降维处理。

3.2.3 副缸调整时调整量降维策略

副缸调整时候情况更为复杂，调整如图9所示。

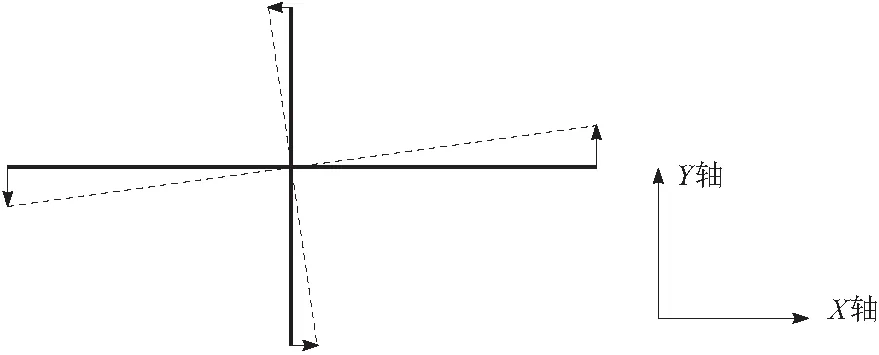
图9 副缸调整图示

可以看到由于副缸调整时，旋转轴与小车顶点拟合平面实际上接近垂直。对于不同位置的对中小车其调整的方向也不尽相同。图9中的四角调整方向近乎垂直，并且不同方向的调整量间也并不存在主要与次要的差别。如果仍然沿袭主缸的调整策略而单纯忽略非副缸方向的调整量必然不会满足要求。因此，需要对调整策略做适当修正。

考虑从主缸调整到副缸调整策略的变化，本质上是从“线”的调整转换为“面”的调整，即在长度以外的部分增加了宽度，从而增大了副缸以外的移动量占比。如图10所示。

图10 主缸调整到副缸调整的变化

在“平面线段”的宽度增加以后带来了其他维度上不必要的多余滑移量，为了降低其他维度的滑移量，解决方法是减少“宽度”。

因为小车阵列的宽度由轨道数和轨道间距决定，所以减少“宽度”无法通过减少实际的宽度来解决。因此，只能从另一个方向着手，即增加旋转阵列的“长度”。在小车阵列确定的情况下，事实上也无法改变阵列的相互长度，但是可以通过平移旋转中心的方法变形增加整体平面的长宽比，如图11所示。

图11 通过移动旋转中心变相增加长宽比

这种平移旋转中心的调整方法本质上并不会减少非副缸方向的多余滑移量，但是可以变相增大在副缸方向上的滑移量，使得实际调整量相对于被动滑移量的比例增加，也能有效降低执行误差。

在进行平移操作以后，可按照调整主缸的策略，舍去非副缸方向的滑移量，将在副缸方向上的移动量作为调整命令发送。实验中，这种调整方式相对于调整主缸效率较低，每次仅能达到目标的60%～80%。工程应用中可以通过多次迭代来消除误差问题。

4 实验验证与性能分析

实验对象为一圆柱筒及其支座构成的移动段，圆筒部分直径约7 m，长度约7 m。其现场照片及最终对接效果如图12所示。

图12 圆筒现场照片及对接效果

具体的对接特征点分布如图13所示。移动段端面8个特征点按照位置命名为A1～A8。其中,前端面(靠近固定段的端面)上4点，最低点为A1，最高点为A3，水平点为A5和A7；后端面(远离固定段的端面)上4点，最低点为A2，最高点为A4，水平点为A6和A8。

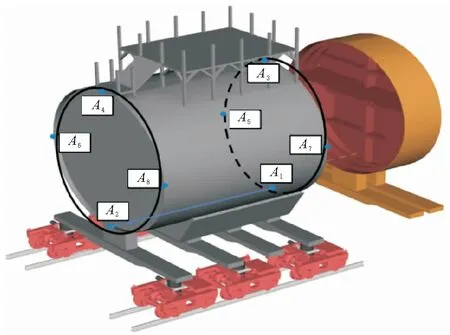
图13 移动段端面特征点

A1A2的连线称为艏艉端中心线。根据艏艉端中心线和坐标轴对齐的方向进行调整，同时根据A2A3的Y坐标偏差调整移动端绕X轴旋转的角度偏差。最终目标是使得A1A2的Y坐标差(偏航角),A1A2的Z坐标差(俯仰角)，A1A3的Y坐标差(横滚角)归零。

对接调整共进行了6次，最终使得A1A2的Y坐标偏差降低到0.74 mm,A1A2的Z坐标差降低到1.53 mm，A1A3的Y坐标差降低到0.20 mm。整体的平移偏差降低到0.11 mm。对接过程数据如表1所示。实验的调整过程偏差变化如图14所示。

图14 实验偏差调整曲线

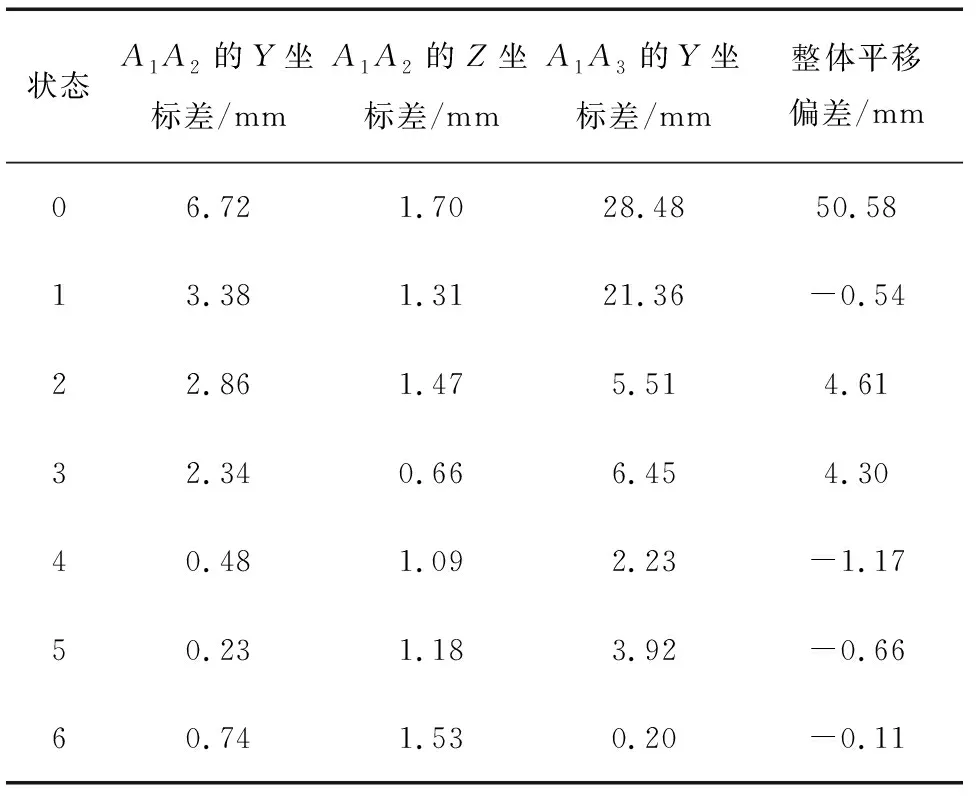
表1 对接过程数据

通过上述结果可以看到，总段最终在各个方向的偏差仅通过个位数次数的调整就达到了对接合拢的精度要求(3个方向的偏差均小于±2 mm)。并且对接解算下达的控制量与目标值实际调整量、总段位姿的判断量数据内部存在非常好的自洽性。能够精确地判断总段当前位姿状态并且将总段调整到设定目标状态。使用该对接解算策略，能够使得总段始终向更好的对接状态迭代靠近。

5 结束语

本文以对中小车为执行系统基础，从总段刚体假设出发，将总段位姿转换为特定点云特征，由点云特征反推总段位姿，并根据总段位姿计算出达到任意调整目标所需要的调整量。为总段智能对接系统提供了总段位姿判断和位姿调整的解算策略。

针对造船业中的日益庞大的总段，使用本系统可以提高对接的精度和效率。应用本对接策略，通过实验验证了其可行性与精度。