后坐力激励下的小型履带机器人位姿变化研究

陈智威，张志安

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

随着感知、运动控制等技术的发展，机器人技术正逐渐成熟并应用到了各行各业中。小型机器人由于体积小、重量轻的特点，十分适合作为武装及侦察机器人由作战人员携带并运用于高危任务，保障前线人员安全，国内外已有相关研究。国外的研究开始较早并已有多种型号投入使用，国内研究则起步较晚，大部分尚处于样机研制阶段[1-4]。

由于这种小型机器人在便携性上的需求，机器人的尺寸和重量都是需要重点把控的参数。尺寸要求便于单人携带，从而限制了武器的布置方案，往往使后坐力方向不能准确通过机器人质心；重量的限制则直接影响机器人的转动惯量、接地摩擦系数等与机器人位姿稳定性相关的参数。因此对于小型机器人来说，武器后坐力对机器人位姿产生的影响是不可忽视的，而过大的位姿变化将直接影响机器人的射击性能。

本文采用有限元法建立了某武装小型履带式机器人的发射动力学虚拟样机模型，对机器人的后坐过程进行了仿真分析，研究了缓冲器参数、负载和发射仰角对机器人在武器发射后坐力下的位姿变化影响[5-7]。

1 机器人有限元模型建立

1.1 机器人结构

本文研究对象为某搭载制式手枪的10 kg级小型机器人,整体尺寸为480 mm×350 mm×20 mm。机器人机械结构主要包括3个模块，分别为底盘模块、俯仰机构模块和武器模块。底盘为无悬架橡胶履带底盘，并搭载电源、处理器等其他设备；俯仰机构采用了蜗轮蜗杆机构，具备自锁能力；武器模块主要包括制式手枪、扳机扣动装置、保险装置和其他配件。

为了保证便携性和隐蔽性，尽可能缩小体积，机器人的整体布置较为紧凑。因此受布局状况所限，机器人搭载的制式手枪需要平躺放置并且枪管轴线相对机器人几何中线有一定程度的偏置。在机器人原始布局中，选择了体积最小化的方案，枪口偏移距离为64 mm。机器人俯视图如图1所示。

图1 小型履带式机器人俯视图

1.2 简化与假设

由于机器人系统组成较为复杂，且本文研究重心在于机器人整体位姿变化，即着重考虑履带与地面的相互作用与相对运动，而不关心局部位置的状态变化。因此为了保证仿真分析精度的同时控制计算量，本文在建立机器人有限元模型时，结合机器人实际情况做出如下简化和假设[8-11]：

a.机器人整体除履带外其他部件均为刚体。

b.机器人各部件之间固定良好，刚性连接部分间均无相对位移，履带与驱动轮啮合面之间无相对位移。

c.机器人非关键部件依据空间位置简化为一刚体，并赋予等效质量与等效转动惯量。

d.机器人驱动轮电机与俯仰电机具有足够扭矩，在发射过程中可保持完全锁止。

e.不计机器人系统的结构阻尼。

f.将武器后坐力简化为作用于枪机底部的均布载荷，数值等于弹底燃气压力，忽略弹丸挤进阻力、膛线导转侧作用在弹带上的力、弹前空气阻力等次要力，忽略火药后效时期对机器人的作用力。

根据上述假设，底盘模块可简化为5个部分，分别为轮系、履带、底盘机架、车头负载和车尾负载5个部分；云台模块简化为1个独立的实体；发射部分可简化为5个部分，分别为发射机架、手枪握把、手枪底座、枪机和发射负载。其中，除履带外各实体均简化为刚体。简化前模型和简化后模型示意如图2所示。

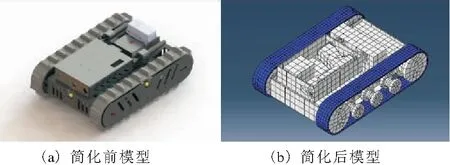
图2 简化前模型和简化后模型

1.3 有限元分析模型的建立

本文使用Abaqus有限元分析软件，采用显式动力学分析求解器进行仿真分析。在有限元模型中，机器人系统简化为9个刚体、2个柔性体、8个固定副和2个平移副。本文研究的小型履带式机器人主要受到5种力，分别为：

a.后坐力。根据前文假设，由于武器发射时受到的枪膛合力等值于弹底燃气压力，而膛内压力可通过内弹道方程组求得。内弹道方程组为

(1)

其中

(2)

查阅文献后可得到相关参数，再通过MATLAB使用四阶龙格库塔法可以得出某型手枪的膛压-时间曲线。某型手枪膛压-时间曲线如图3所示[12]。

图3 某型手枪膛压-时间曲线

b.摩擦力。根据机器人的实际定位，本文以在混凝土地面运行的工况为例进行仿真计算，查阅文献后取机器人与地面滑动摩擦系数φ为0.55，采用罚函数摩擦模型[13]。

c.重力。本文取重力加速度g为9.8 m/s2，根据机器人虚拟样机易得机器人所受总重力为99.96 N。

d.复进簧作用力。查阅文献可得某型手枪相关参数，本文取复进簧刚度系数为0.78 N/mm,使用Translator连接器模拟复进簧的作用[12]。

e.缓冲器作用力。本文第3节算例中将在有限元模型中添加缓冲器，并以缓冲器参数作为变量进行研究。此处根据常见缓冲器型号参数，取缓冲器弹簧刚度系数k为1～8 N/mm，取缓冲器阻尼系数c为0.5～4.0 N·s/mm，使用Translator连接器模拟缓冲器的作用[14]。

最后添加地面约束，进行实体网格划分，即完成有限元分析模型的建立。

2 后坐力对机器人位姿变化影响分析

2.1 位姿变化坐标系的建立

为了描述机器人的位置与姿态变化过程，本文以机器人几何中心为原点，枪口朝向为Z轴正方向，垂直于地面向上为Y轴正方向，建立一个与机器人固连的笛卡尔坐标系OXBYBZB，称之为机器人坐标系，下文以{B}表示；以机器人坐标系初始位置建立一个固定参考坐标系OXAYAZA，下文以{A}表示。通过对机器人坐标系{A}相对于参考坐标系{B}的表达，即可以描述机器人的位姿变化情况[15]。机器人坐标系如图4所示。

图4 机器人坐标系

关于位置描述，本文使用一个3×1的位置矢量U对机器人进行固定参考坐标系中的定位,矢量各个元素分别用下标x,y,z来标明：

(3)

关于姿态描述，为了更合理地表达机器人的姿态变化情况，本文采用Y-X-Z欧拉角坐标系表示法。该描述姿态的方法为：首先将机器人坐标系{B}与参考坐标系{A}重合,并将{B}绕YB旋转α角，再绕XB旋转β角，最后绕ZB旋转γ角。坐标系{B}进行三次欧拉角变换的坐标轴变化情况如图5所示。

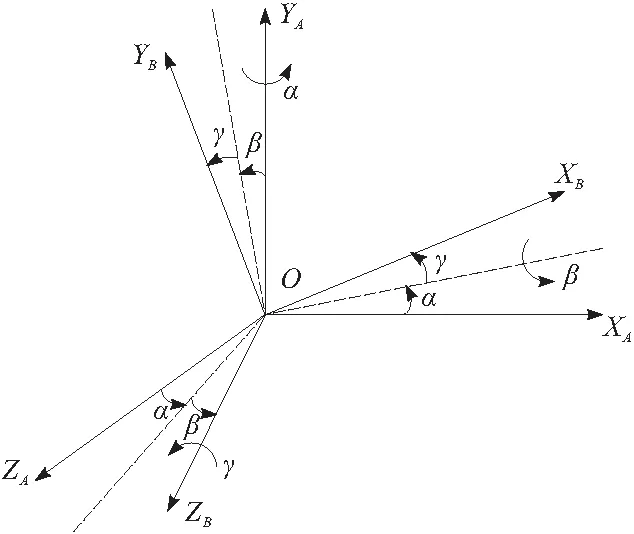
图5 Y-X-Z欧拉角坐标系

2.2 缓冲器阻尼与弹簧影响分析

为了研究缓冲器的使用及其参数的变化对机器人在后坐力下的位姿影响，结合常见的缓冲器参数，本文对阻尼系数在0.5～4.0 N·s/mm和弹簧刚度在1～8 N/mm的缓冲器进行了仿真分析。不同缓冲器参数下的机器人总位移变化情况如图6所示。

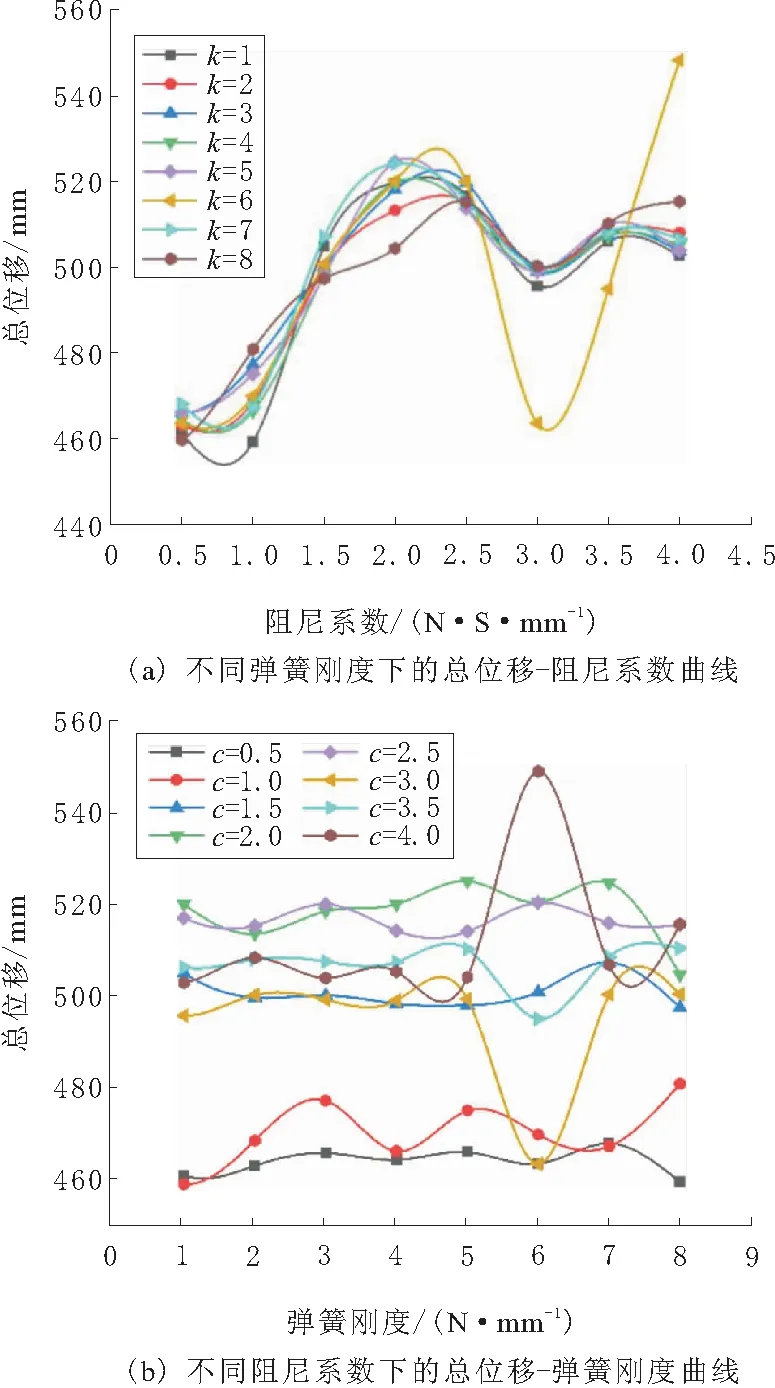
图6 总位移量与缓冲器弹簧刚度和阻尼系数关系曲线

由图6可以知道，阻尼系数对于机器人最终位姿的影响较大。当阻尼系数从0.5 N·s/mm到2.0 N·s/mm时，机器人的最终位移量逐渐增大，并在2.0 N·s/mm时达到峰值，随后开始出现下滑，最后最终位移量在稳定500 mm上下波动；而弹簧刚度对于机器人最终位姿的影响并不显著，机器人的最终位移量随着弹簧刚度的增加出现小幅的波动。

要注意的是，缓冲器效果在弹簧刚度为6 N/mm时出现较大的波动。此处猜测是由于随着阻尼系数与弹簧刚度的变化，机器人系统的固有频率和共振频率也在随之变化；而当系统的共振频率与武器击发对系统的激励频率接近时，系统会产生一定程度的共振现象，从而对机器人最终的位姿产生影响。

由于弹簧刚度对于总位移量的影响较小，且弹簧刚度与缓冲器的总质量呈正相关，因此认为弹簧刚度1 N/mm为缓冲器最优选择。在弹簧刚度为1 N/mm时，阻尼系数与相应的机器人最终位姿的关系如表1所示。

表1 阻尼系数与相应的机器人最终位姿

结合仿真结果并综合考虑缓冲器的重量，可认为弹簧刚度为1 N/mm，阻尼系数为0.5 N·s/mm的缓冲器，是减小机器人在后坐力作用下总位移量的最优选择。

2.3 发射仰角与负载影响分析

在反恐机器人的实际运用中，机器人的负载与仰角往往随着实际情况发生改变。此处将研究负载与发射仰角对机器人最终位姿的影响，从而得出负载与仰角对于机器人位姿参数的关系。不同负载、不同仰角下机器人后座过程中的速度-时间曲线如图7所示。

由图7可知，机器人的后坐过程可以分为3个阶段。第1阶段，机器人的速度在短时间内迅速提升，达到峰值；在第2阶段，机器人的速度开始出现波动并逐渐下降；在第3阶段，机器人的速度开始均匀下降，并最终停止。

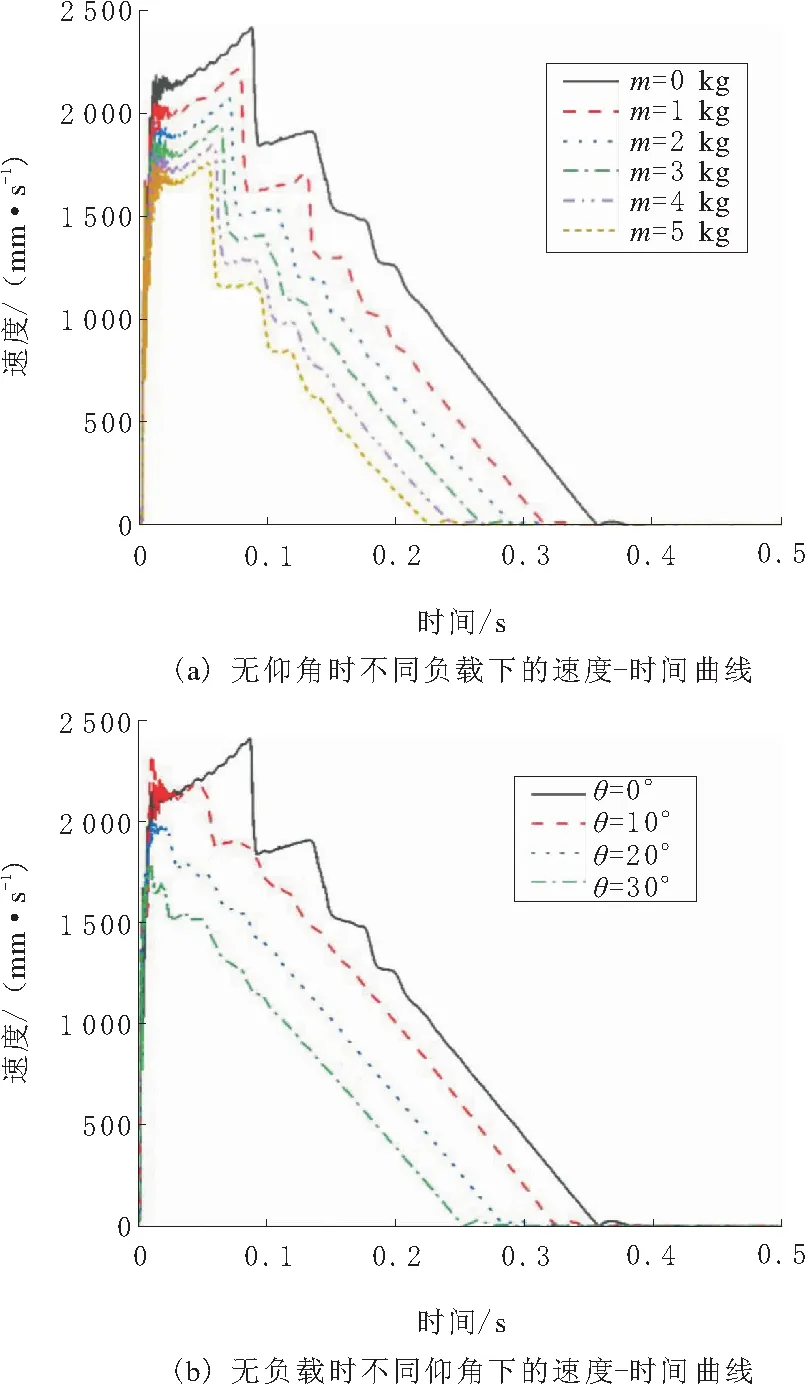
图7 不同负载和仰角下的速度-时间曲线

结合机器人射击的实际工况和仿真结果来看，不难得出机器人在武器击发后的运动方式和规律。随着武器的击发，子弹出膛过程产生的膛压对机器人产生巨大的反作用力，并持续数毫秒后随着子弹的出膛开始迅速衰减，该过程对应着机器人的后坐过程第1阶段；在子弹出膛带来的巨大冲量下，机器人将出现多次弹起-触地的动作，从而导致了速度的大幅度波动，该过程对应着机器人的后坐过程第2阶段；随着机器人的动能不断减小，当机器人不再弹起后，机器人进入仅与地面发生相对滑动的过程，速度开始均匀下降，并最终停止，该过程对应着机器人的后坐过程第3阶段。

从图7可以看到，随着负载和仰角的增大，除了机器人的峰值速度显著降低和后座运动持续时间显著减小外，机器人的后坐运动过程变化主要发生在第2阶段。当仰角不变，负载变大时，第2阶段的持续时间也随之减少，但速度波动程度几乎没有变化；当负载不变，仰角变大时，第2阶段的持续时间和速度波动程度出现显著降低，当仰角达到30°时，第2阶段几乎消失，即机器人在后坐过程中几乎不再弹起。

由于第2阶段的存在不利于机器人位姿的迅速调整，因此可以得出结论，在机器人的需要执行射击动作时应尽可能保持高仰角射击。

2.4 最终位姿回归分析

在机器人的实际射击工况中，往往需要对同一个目标进行连续、多次的打击，但由于机器人位姿变化过大的原因，在机器人初次瞄准目标后，需要在每次射击后迅速做出位姿的修正，以保证后续射击的准确性。而机器人的负载与发射仰角通常会随着实际情况发生改变，因此，为了提高机器人位姿修正效率以及实现自动修正功能，本文通过有限元分析结合回归分析的方法，进一步研究了机器人的负载及仰角与最终位姿的关系。

由于机器人在后坐力作用完成后必然停止于二维平面内，故位置方面Uy必然归零，姿态方面β和γ必然归零，因此可以用Uz，Ux，α等3个变量来描述机器人在后坐力作用下的最终位姿。不同负载下机器人的最终位姿参数与仰角的关系曲线如图8所示。

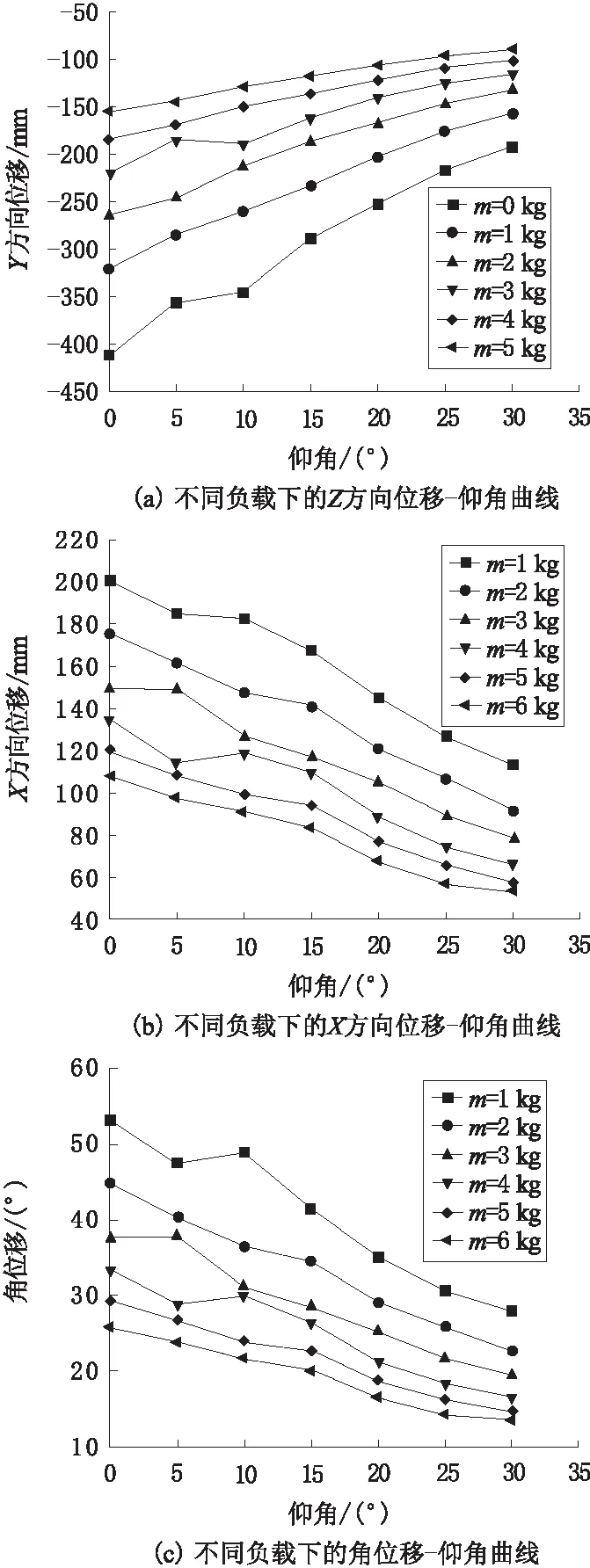
图8 机器人最终位姿与负载和仰角关系曲线

由图8可知，不管是机器人的位移量还是角位移量，都随着负载和仰角的增加而显著减小，但显然并不是线性的减小。此处本文采用二次多项式来对机器人最终位姿参数与负载和仰角的关系进行拟合。拟合得出的二次多项式回归方程为

(4)

Uz为沿ZA轴方向位移；Ux为沿XA轴方向位移；α为绕YA轴偏转角；m为机器人负载质量；θ为云台仰角。

拟合得到的关于Uz、Ux和α的回归方程决定系数R2分别为0.992 34、0.990 92和0.986 26，说明该回归方程具有较高的拟合程度。

公式(4)可应用于机器人射击后的位姿快速修正，研究方法对于同类型机器人相关研究具有借鉴意义。但机器人后坐过程中，具体位姿参数变化机理仍需进一步研究。

3 结束语

对于偏置搭载某型手枪的10 kg级履带式机器人，可以得出以下结论：

a.缓冲器对于机器人在后坐力作用下的位移量有一定抑制作用。其中弹簧刚度的影响较小，对于位移量的影响无明显趋势；阻尼系数的影响较大，在2 N·s/mm左右机器人的总位移量达到峰值。

b.机器人在后坐力下的位姿变化程度随着发射仰角与负载的增加而显著减小，其中发射仰角的增加能够有效抑制机器人在后坐过程中的跳动现象。

c.在负载为0～5 kg，仰角为0～30°的范围内，二次多项式能够较好地拟合发射仰角和负载与机器人最终位姿参数的关系。