地铁受电弓故障模式分析及危害度评估

宫 琦，陈秉智，李永华，刘思文，夏 清

(1.大连交通大学机械工程学院，辽宁 大连 116028；2.大连交通大学机车车辆工程学院，辽宁 大连 116028)

0 引言

受电弓是轨道车辆获得电能最重要的高压设备，是地铁车辆电气牵引系统的薄弱环节，因此对受电弓进行故障模式分析及危害度评估，确定影响地铁受电弓可靠性的关键因素，对保证地铁车辆安全运营服务具有重要的实际意义。

近年来，研究人员对受电弓可靠性分析的较多[1-4],对地铁受电弓故障模式危害性分析的很少，而故障模式危害性分析在铁道车辆、铁道车辆重要系统及其他工业领域研究较多[5-10]。

在此,为了对受电弓故障模式进行更为科学的、合理的危害度评估，鉴于受电弓故障模式的影响因素具有复杂性和模糊性，本文运用改进模糊层次分析法、熵权法和模糊综合评判方法对地铁受电弓故障模式的危害性进行定量分析。专家打分应用三角模糊数表示，在专家打分的基础上采用层次分析法确定各类影响因素的主观权重[11]，由于专家的知识、经验和偏好不同，引入专家权重系数，对主观权重加以修正；采用熵权法确定各类影响因素的客观权重[12]，根据得出的主观权重和客观权重确定各类影响因素的精确组合权重，基于模糊综合评判方法完成受电弓故障模式的危害度定量计算，依据得到的定量计算结果优先排序确定影响地铁受电弓可靠性的关键因素，提出提高受电弓可靠性的改进措施，从而对受电弓的故障维修提供指导。

1 地铁受电弓结构和可靠性

1.1 受电弓结构

结构图能清楚地说明一个功能系统、子系统和单元部件的相关性、复杂性。

受电弓主要由底架、气囊、钢丝绳、下臂、拉杆、上臂、平衡杆和弓头等组成。升弓驱动气囊安装在底架上，气囊充气后，通过钢丝绳作用于下臂,带动连杆机构运动，从而实现升弓。供给气囊的气路断气后，受电弓靠自身自重实现降弓。地铁受电弓结构如图1所示。

图1 地铁受电弓结构

1.2 受电弓可靠性框图

可靠性框图属于一种逻辑图，其从可靠性方面分析系统与子系统、部件之间的关系，并能够体现部件状态对系统状态的影响。

1.2.1 服务故障

服务故障是指由于某一特定功能无法完成从而导致的车辆晚点(停车3 min以上)，甚至停止运营，需要另一列车将其拖回车辆基地或疏散乘客，车辆空车返回车辆基地。由于受电弓故障而导致地铁列车出现服务故障时,受电弓可靠性框图如图2所示。

图2 受电弓“服务故障”可靠性框图

1.2.2 延误故障

延误故障(延误不超过3 min)是指因某一特定功能不能实现而导致列车停车时间不超过3 min，且不影响商业运营。由于受电弓故障而导致地铁列车出现延误故障时,受电弓可靠性框图如图3所示。

图3 受电弓“延误故障”可靠性框图

1.2.3 维护故障

维护故障(碎修、列检故障)是指车辆在运营过程中或在检查过程中,分别由司机或检修人员发现的故障。地铁车辆在碎修、列检过程中发现受电弓故障，此时受电弓可靠性框图如图4所示。

图4 受电弓“维护故障”可靠性框图

2 危害度综合评判的理论方法

本文构建的危害度综合评判主要由以下6个部分组成：

a.建立因素集、因素等级集和评价集，明确影响因素及评价标准。

b.构造影响因素的三角模糊判断矩阵，得到原始主观因素。

c.引入专家系数，确定影响因素主观权重。

d.依据客观数据，采用熵权法，确定客观权重。

e.基于组合赋权确定影响因素的综合权重。

f.实现模糊综合评判，获得各故障模式的危害度大小。

具体危害度综合评判流程如图5所示。

图5 危害度综合评判流程

2.1 改进模糊层次分析法

2.1.1 建立因素集及评价集

因素集是对评价对象有影响的各类因素的集合,用U表示为

U={u1,u2,…,un}

(1)

ui为对该事物有影响的第i个因素(i=1,2,…,n)。

评价集是由领域专家对评价对象作出的评价等级的集合,用V表示为

V={V1,V2,…,Vm}

(2)

m为可能的评判结果个数。

2.1.2 构造模糊判断矩阵

将三角模糊数与层次分析法结合，能更好地解决专家决策的不确定性，使得层次分析法中的专家评分更科学。

设有实数集R=(-∞,+∞)上的一个模糊数M，当它的隶属函数μM：R→[0,1]满足下列式时，称其为三角模糊数。

(3)

l≤m≤u，l和u分别为M支撑的上界和下界，而m为M的中值，三角模糊数M可记为(l,m,u)。

由专家对各因素进行两两比较，并将比较结果以一定的标度定量化，构成两两模糊判断矩阵。假设有n个评价因素，则判断矩阵为

(4)

qij是一个三角模糊数M(lij,mij,uij)。其中，lij、uij表示判断的模糊程度，u-l越大，表示判断越模糊，u-l越小，表示判断越清楚；中值mij的取值依据层次分析法的9标度法确定。

(5)

为了避免由于专家的知识、经验和偏好不同而导致的误差性大，引入专家权重系数，对得到的各影响因素权重w加以修正，以获得合理的主观权重A。

设有k位专家打分，则第s位专家的权重系数计算式为

Pk=as×bs×cs×ds×es

(6)

as、bs、cs、ds和es分别为专家的学历、职称、工作年限、对问题熟悉程度和评价自信度，对应的具体分值如表1所示[15]。

表1 家权重系数分值表

对专家权重系数Pk进行归一化处理为

(7)

则引入专家权重系数βs的主观权重A为

A=βs×ws

(8)

2.2 熵权法

熵权法是客观赋权法，为了消除层次分析法求解的权重带有主观因素，因此引入熵权法。熵权法从各影响因素的变异情况出发，计算各个影响因素的权重，对各影响因素权重的修正采用得到的熵权完成，使危害度综合评价影响因素体系的权重较为客观。

对初始评价矩阵进行标准化处理，得到标准化矩阵F，其计算公式为

(9)

rij为第i位专家给第j个影响因素的评价值。第j个影响因素的熵值ej的表达式为

(10)

第j个影响因素的熵权A′的表达式为

(11)

1-ej为各影响因素的差异性系数，其值越大说明影响因素对总体的影响越大;A′值越大，说明这个影响因素的影响作用越大[16]。

2.3 组合权重确定

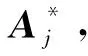
(12)

Aj为改进模糊层次分析法计算得到的主观权重；Aj′为熵权法计算得到的客观权重。

2.4 危害度确定

考虑到不丢失单因素的评价信息，利用加权平均模型M(∘,+)[17],根据系统影响因素的组合权重和单因素评判矩阵,对各故障模式进行综合模糊评判，得到一级评判结果。

分析各影响因素对于评语集中评价等级的隶属度，建立单因素评判矩阵。其中,采用专家评判法,统计分析确定隶属函数和单因素评判矩阵。

则一级模糊综合评判模型为

B=A*∘R

(13)

A*为影响因素的组合权重；R为单因素评判矩阵。

根据各故障的一级模糊综合评价结果和危害等级进行危害度综合，即

W=BVT

(14)

3 算例分析

为了不影响地铁车辆的运营服务，采用改进模糊层次分析法和熵权法,进行受电弓发生服务故障时其故障模式的危害度计算。

3.1 受电弓故障模式

由图2受电弓“服务故障”可靠性框图可知，影响地铁车辆运营服务故障情况下受电弓的故障模式主要有4种：天平组焊、钢丝绳组合、调整钢丝组合和杆端关节轴承，分别对受电弓的这4种故障模式进行危害性分析。

3.2 改进的模糊层次分析法

3.2.1 建立因素集U及评价集V，确定因素等级集

通过对受电弓故障模式、原因及影响的调查和分析如表2所示，确定影响受电弓故障危害性评价的因素主要有：故障发生度、严酷度、可探度和维修度。因此，评价的因素集为U= [发生度等级 严酷度等级 可探度等级 维修度等级]

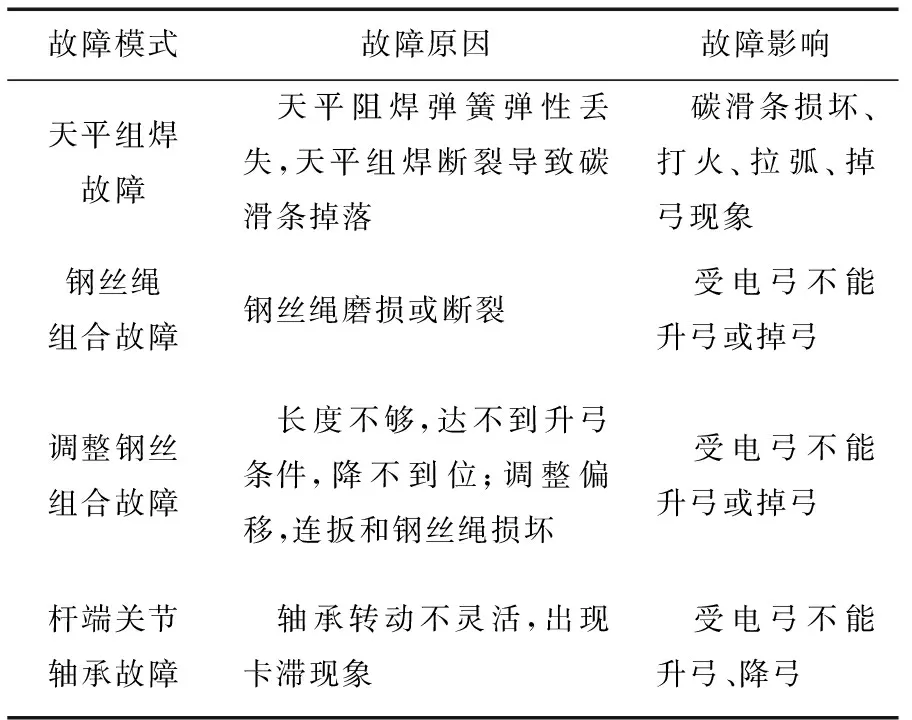
表2 受电弓故障模式、原因及影响分析

受电弓故障危害度的评价集V可分为5个等级，即V=[1 2 3 4 5]，每个等级对应的意义如表3所示。

表3 危害度评价等级及其含义

因素集和评价等级集对应关系及分值如表4所示。

表4 因素评价等级及分值

3.2.2 建立单因素评判矩阵

聘请5位专家分别对4种故障模式影响因素进行评价，得到一级模糊单因素评判矩阵R。以 “天平组焊故障”为例,采用专家评判法、统计分析得到故障发生度的单因素评价集为

同理可得严酷度、可探度和维修度的评判集，构成评判矩阵为

按照故障模式“天平组焊故障”的方法，依次构造“钢丝绳组合故障”、“调整钢丝组合故障”和“杆端关节轴承故障”的因素集评判矩阵，分别为：

3.2.3 计算影响因素的主观权重集

以“天平组焊故障”为例计算影响的组合权重。将评价结果采用三角模糊数表示，构造出各影响因素的模糊判断矩阵，根据式(5)对模糊判断矩阵进行去模糊化处理和一致性检验，分别如表5～表9所示。

表5 专家1给出的各影响因素模糊判断矩阵

表6 专家2给出的各影响因素模糊判断矩阵

表7 专家3给出的各影响因素模糊判断矩阵

表8 专家4给出的各影响因素模糊判断矩阵

表9 专家5给出的各影响因素模糊判断矩阵

用矩阵表示5位专家给的各影响因素的权重：

w1=[0.467 9 0.340 8 0.056 6 0.134 8]

w2=[0.505 7 0.292 6 0.066 8 0.134 9]

w3=[0.540 7 0.230 9 0.072 5 0.155 9]

w4=[0.551 2 0.230 4 0.077 8 0.140 5]

w5=[0.465 8 0.308 5 0.072 5 0.153 2]

根据表1，结合5位专家的个人信息，由式(6)和式(7)可得专家权重系数βs为

βs=[0.038 4 0.034 1 0.017 1 0.364 2 0.546 2]

根据式(8)可得故障模式“天平组焊故障”的主观权重为

A1=[0.499 6 0.279 4 0.073 6 0.147 3]

3.2.4 计算影响因素的组合权重集

由5位专家根据表4各等级对应的分值进行打分构造初始评价矩阵，如表10所示。

表10 初始评价矩阵

根据式(9)～式(11)，计算得到故障模式“天平组焊故障”的客观权重为

A′=[0.350 7 0.163 2 0.110 0 0.376 2]

根据式(12)可得故障模式“天平组焊故障”的组合权重为

按照故障模式“天平组焊故障”组合权重的计算方法，依次计算“钢丝绳组合故障”“调整钢丝组合故障”“杆端关节轴承故障”的组合权重分别为

3.3 一级模糊综合评判及危害度确定

由式(13)一级模糊综合评判模型,可得：

B1=A1∘R1=

[0.616 3 0.160 4 0.028 5 0.194 9]∘

[0.532 0 0.295 1 0.140 9 0.032 1 0]

根据式(14)，可以计算得到故障模式“天平组焊故障”的危害度为

W1=B1VT=

[0.532 0 0.295 1 0.140 9 0.032 1 0]∘

由此依次得到故障模式“钢丝绳组合故障”“调整钢丝组合故障”“杆端关节轴承故障”的一级模糊评判矩阵及其危害度分别为：

B2=[0 0.232 1 0.368 7 0.399 4 0]，

W2=3.167 9

B3=[0.607 1 0.328 8 0.064 4 0 0]，

W3=1.457 9

B4=[0 0.200 0 0.622 7 0.177 5 0]，

W4=2.978 1

由上述的计算结果可得：W2>W4>W1>W3,即受电弓发生服务故障时各主要故障模式危害度由大到小依次为钢丝绳组合故障、杆端关节轴承故障、天平组焊故障和调整钢丝组合故障。从各故障模式的W值能发现，钢丝绳组合故障虽然发生频率不高，但该故障发生后的严重程度很高、维修难度大导致其危害度最大；杆端关节轴承故障虽然也不常发生，但因其维修难度大而使其危害度偏大；调整钢丝组合故障虽然比天平组焊故障发生的概率大，但由于天平组焊故障的严重程度和维修难度比调整钢丝组合故障大，所以天平组焊故障的危害度比调整钢丝组合的危害度要大。根据以上结果，加大对危害度高的故障模式的检查频率，对故障、损坏件及时进行更换，可以及时消除或减少该故障模式。

4 结束语

本文基于熵权法、改进的模糊层次分析法和综合评判，对地铁受电弓故障模式的危害度进行分析评估，可得如下结论：

a.针对地铁车辆服务故障、延误故障和维护故障3种故障类型，对地铁受电弓进行深入分析，建立不同故障类型下的受电弓可靠性模型，考虑了受电弓故障发生度、严酷度、可探度和维修度4个影响因素,以更有针对性地合理客观地对受电弓故障模式危害度进行分析评价。

b.将熵权法、改进的模糊层次分析法和综合评判有机结合，进行受电弓故障模式危害性的定量分析，可以将三角模糊数用到故障模式影响因素的判断矩阵中，以考虑各种模糊不确定性因素的影响；引入专家权重系数，可以降低在权重确定过程中因专家水平不同而导致的评价结果的主观性差异；采用熵权法，可以消除层次分析法求解的权重带有主观因素；组合权重的确定过程既考虑了主观因素又考虑了客观因素，使权重更加科学，综合评判结果更加准确合理，在一定程度上丰富和发展了危害度评价方法。

c.根据综合评判结果，对受电弓不发生服务故障时的各故障模式危害度的大小进行优先排序：钢丝绳组合故障>杆端关节轴承故障>天平组焊故障>调整钢丝组合故障。说明本文提出的受电弓危害度综合评判方法是可行的、适用的，为改进受电弓结构设计、提高其可靠性以及制定合理的维修策略提供了科学的决策依据。