技能映射下学习空间判别定理

赵 青，韩光明，梁 娟

（闽南师范大学数学与统计学院，福建漳州363000）

学习空间理论是在知识空间理论的基础上发展而来的.知识空间理论[1-2]是Doignon 和Falmagne 于1985年提出的以集合论和组合数学为基础的知识表示和自适应评估理论．它的基本思想是通过学生对某学科一些问题的应答情况，得出能够解释一切应答反应的问题集合．这个问题的集合就刻画了学生当前的知识水平．由于确定学生知识水平的过程实质上反映了学生的学习过程，因此在知识空间理论的基础上发展出了遵循教学基本规律的学习空间理论[3]．

目前该理论在美国和欧洲不仅广泛的用于测评个体的知识水平和自适应教学，如计算机教育系统ALEKS，RATH 和APeLS 等，还成功地用在设备错误分析、医疗诊断和模式识别等领域[3]．国内对知识空间理论也有一定的研究.孙波和傅骞[4-5]从理论上概述了技能结构相关内容，对比研究了知识空间理论与项目反应理论.杨文正等[6]运用知识空间理论分析概念图，增强了概念图的教学功用.苗夺谦等[7]研究了知识空间的粒度空间模型.麦裕华等[8]应用知识空间理论分析了学生的氧化还原反应学习情况.李进金等[9]通过知识空间的基建立了知识空间和形式背景间的联系.

在知识空间理论中，个体的知识水平不仅可以由问题集刻画[10-14]，还可以由技能集刻画.为了更高效的表示知识，Falmagne等[14]等在认知能力的基础上建立了问题和技能之间的联系，给出了技能函数和问题函数的雏形．在此基础上，Doignon[15]引入了技能映射的概念，根据解决问题所需技能间的“或”、“与”关系，提出了析取模型和合取模型．随后，学者们针对基于技能的扩展知识空间展开了深入的研究[16-18].

同一个技能映射，析取模型下导出的是知识空间[16]，合取模式下是闭包空间[18]．两种情况下，他们都不一定是学习空间．学习空间作为基于教学规律的特殊的知识结构，在解释个体知识水平评估结果，确定学习方向等方面有明显的优势．因此，探讨技能映射和学习空间的关系是很有意义的.

由于学习空间的判别方法[3]一般都是基于所有知识状态或者原子间关系给出的，而技能映射下导出知识结构的过程也需要遍历技能子集，因此按照常规方法来判定导出的知识结构是否是学习空间会导致大量的计算.这就要求我们根据技能模型的特点，寻找高效的判定方法.事实上，析取模型下每项技能所能解决的问题集有可能是所诱导出的知识空间的原子，这就为我们直接在技能映射下寻找诱导出学习空间的条件提供了可能.虽然我们的方法不必求出所有的原子，省去了大量的计算过程，但其本质是建立在原子上的.于是，本文首先给出了基于原子的学习空间判别定理，在此基础上探讨了析取模型下导出学习空间的条件.然后利用合取模型与析取模型导出的知识结构的对偶性，得到了合取模型下导出学习空间时技能映射需满足的条件.

1 预备知识

在知识空间理论中，知识是用问题的集合来表示的．我们将能够反映某领域知识的所有最基本的有代表性的问题的集合称为问题域，用Q表示．类似的，将解决Q里问题所需的方法、算法和技巧等的集合称为技能域，用S表示．

知识空间理论中最核心的概念就是知识状态和知识结构．前者由理想状态下个体能正确解决的问题组成，体现了个体的知识水平，后者是知识状态的集族，呈现了知识的组织形式．

定义1[2]设Q是非空问题域是含有Q和∅的Q的子集族，称K∈知识状态(Q，)为知识结构．若是并封闭的，则称(Q,)是知识空间．

若Q有限，我们称(Q，)是有限的；若有限，则称(Q，)是本质有限的．教育背景下关于某领域知识的都是本质有限的，并且通过约简可以转化为有限问题域上的知识结构．

定义2[2]若′是由的子集族的并构成的集族，即∀⊆，有∪∈′，则称′是的张成或张成′，记作′=().

定义3[2]若()=且∀⊆，()=，有=，则称是的基.

定义4[3]若知识结构(Q，)满足下列两个条件，则称其为学习空间．

[L1]∀K,L∈，若K⊂L，则存在有限状态链K=K0⊂K1⊂…⊂Kp=L使得|KiKi−1|=(1 ≤i≤p)，并且|LK|=p;

[L2]∀K,L∈，∀q∈Q，若K⊂L且K+{q} ∈，则L∪{q} ∈．

注L2中的+表示不相交的并，即q∉K.

公理[L1]和[L2]反映了教育学中两条最基本的教学规律：循序渐进的原则和保持学习的连贯性.

如果集族里任何两个集合都可以通过彼此仅相差一个元素的集合序列联系起来，并且序列中所有集合都属于此集族，这个集族就是良级的.学习空间一定是良级知识空间，反之亦然.此外，学习空间一定是可辨识的，即问题域中不存在具有同样信息的问题，否则无法保证任意两个知识状态间都存在紧路径.一个不可辨识的知识结构通过约简可转化为可辨识的.通常我们考虑的知识结构都是可辨识的.

定义5[3]称三元组(Q,S,τ)为一个技能映射，其中Q为非空问题域，S为非空技能域，映射τ:Q→2S{∅}.

当Q和S明确时，有时也直接称τ为一个技能映射.定义里的S可以是无限集，例如可以用实数集来表示某种能力水平.但在实际应用中，S都是有限的.

∀q∈Q，τ(q)∈2S{∅}即为与问题q的求解相关的技能集合.∀s∈S，用τ−1(s)来记和技能s相关的Q中问题的集合，即τ−1(s)={q∈Q|s∈τ(q)}.如果删除任意一个技能会改变导出的知识结构，则称此技能映射为极小技能映射.相应地，将去掉了冗余技能的技能集称为极小技能集.有限知识空间一定存在极小技能映射.极小技能映射不唯一时，彼此同构.

本文只考虑Q和S有限的情况.本节涉及的未详细阐述的概念和结论，请参考文献[3]及[18].

2 析取模型和合取模型

个体的知识状态可以由技能决定，因为只有掌握了相应的技能才能解决问题.析取模型和合取模型是技能与知识状态间常见关系的形式化.

定义6[3]设(Q,S,τ)是一个技能映射，T⊆S，则K={q∈Q|τ(q)∩T≠∅}称为析取模型下由技能集T确定的知识状态.

定义7[3]设(Q,S,τ)是一个技能映射，T⊆S，则K={q∈Q|τ(q)⊆T} 称为合取模型下由技能集T确定的知识状态.

析取模型意味着要解决问题q，个体至少需掌握τ(q)中的一项技能;而合取模型则要求个体必须掌握τ(q)中的所有技能才能解决问题q．

当个体具有的技能T取遍S的子集时，可得依析取模型和合取模型导出的所有知识状态的集合，分别记作和显然和都是知识结构.

依上述两个定义，我们发现

1)∀s,t∈S，若τ−1(s)=τ−1(t)，则在诱导或时，s和t的作用一样，可认为是同一种技能，去掉s或t中任何一项技能不会改变诱导的知识结构.

2)∀a,b∈Q，若τ(a)=τ(b)，则无论是还是中，凡是含有a的状态一定含有b.从知识掌握角度看，即个体若掌握了a，就一定会掌握b，反之亦然，问题a和b含有的信息是一样的.此时的知识结构无法区分a和b，是不可辨识的.此种情况下，和都不可能是学习空间.

例1设Q={a,b,c,d}，S={s,t,u,v}，定义 技 能映射τ:Q→2S{∅} 为τ(a)={s,t,v}，τ(b)={u}，τ(c)={t,u}，τ(d)={s,t,v}.

此例中τ−1(s)= τ−1(v)，去掉s或v中任一技能后诱导出的和保持不变.因为τ(a)τ(d)，说明问题a和d体现了同样的信息.无论是还是中，我们看到凡是含有a的状态一定含有d，因此，和都不可能是学习空间.

定理1[3]设(Q,S,τ)是一个技能映射，则是知识空间，是简单闭包空间且相互对偶.

3 析取模型下学习空间判别定理

目前，学者们已从不同角度给出了学习公理的等价形式[3，19].因为析取模型下单项技能所能解决的问题集和导出的知识空间的原子间存在联系，所以本节先给出了基于原子的学习空间判别定理，然后在此基础上提出了析取模型下的学习空间判别定理.

引理1[3]设是有限集族，()是的张成，则下面两个条件等价.

2)∀q∈，∀G∈，若G是q的极小集，则G{q} 是的子集族的并.

定理2是学习空间的基

定理2 是引理1 的推论，在文献[3]和[19]中也有其他形式的类似结论.若是学习空间的基，那么中的原子只能是唯一一个问题的原子，即∀B∈σ(q)，当B≠{q} 时需要注意的是，此时q∈⋃可能存在多个原子，即有可能|σ(q)|＞1.

推论1设是学习空间的基，则

证明因为⋃中任何一个问题都有原子，所以若，则中至少有一个原子是多个问题的原子，矛盾.

引理2设(Q,S,τ)是技能映射，A{τ−1(s)|s∈S}，则τ,∨= S(A).

证明K∈τ,∨⇔∃T⊆S，s.t.K ={q∈Q|τ(q)⋂T≠∅}

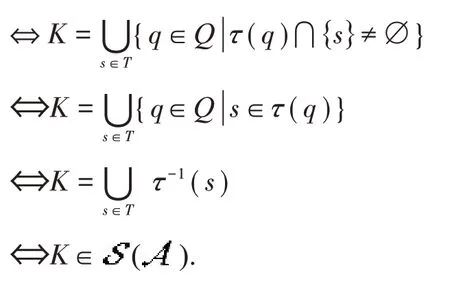
定理3设(Q,S,τ)是技能映射，={τ−1(s)|s∈S}，则τ,∨是学习空间

证明设是τ,∨的基，由引理2，Kτ,∨=()，有⊆.先证必要性：∀A∈A，若A∈，由定理2 知若则再证充分性：∀A∈，若则A∌.若则不仅A∈，而且还是唯一问题的原子.这说明中的知识状态，要么不是原子，要么仅是唯一问题的原子.由定理2可推断τ,∨是学习空间.

推论2设(Q,S,τ)是技能映射，若|S|＜|Q|，则不是学习空间.

由引理2和推论1易证.

4 合取模型下学习空间判别定理

利用合取模型和析取模型下分别导出的知识结构的对偶性，在第4 节内容的基础上，提出了合取模型下的学习空间判别定理.由于(Q,S,τ)依合取模型诱导的是交封闭的知识结构，而学习空间一定是并封闭的，可辨识的.因此只需要研究τ在何种情况下诱导的是并封闭的.又因为和是对偶的，所以我们可将问题转化为研究既是并封闭又是交封闭的条件，即是拟序空间的条件.

引理3[20]知识空间(Q，)是交封闭的⇔∀q∈Q有|σ(q)|=1.

根据引理3，(Q，)若是拟序空间，则∀q∈Q只有唯一的原子，反之亦然.

定理4设(Q,S,τ)是技能映射，S′是析取模型下S的极小技能集，则τ,∧是学习空间Q与{τ−1(s)|s∈S′}一一对应.

证明由于τ,∧是交封闭的，则是学习空间⇔是序空间，即可辨识的拟序空间.又和相互对偶，因此τ,∧是拟序空间⇔是拟序空间.下面证明，τ,∧是可辨识的⇔是可辨识.∀q∈Q，设即τ,∨(q)是τ,∨中所有含有问题q的知识状态集族.若τ,∨不可辨识，则至少则说明τ,∧不可辨识，反之亦然.因此，是序空间⇔是序空间.而是序空间⇔是∀q∈Q只有唯一原子的学习空间⇔Q与的基是一一对应的.而当S′是析取模型下S的极小技能集时，{τ−1(s)|s∈S′} 就是的基.命题得证.

5 结束语

学习空间作为一种特殊的知识空间，能够通过学生的知识水平评估结果，给予师生更加自然和简洁的教学指导.但是给定一个技能映射，由它导出的知识结构却不一定是学习空间.本文在基于原子的学习空间判别定理的基础上，提出了依析取模型和合取模型诱导学习空间时技能映射需要满足的条件.这些结果丰富了技能映射和学习空间的联系.后续我们准备将本文的成果应用到教学实践中，并试图直接在技能映射下寻找关键学习路径.