非一致格子上离散分数阶差分与分数阶和分

程金发

（厦门大学数学科学学院 福建 厦门，361005）

1 背景回顾及问题提出

正如我们在本文序言指出的，分数阶微积分的概念几乎与经典微积分同时起步，可以回溯到Euler和Leibniz时期.经过几代数学家的努力，特别是近几十年来，分数阶微积分已经取得了惊人的发展和广阔的应用，有关分数阶微积分的著作层出不穷，例如文献[1-4]，但是在一致格子x(z)=z和x(z)=qz或者q−z,z∈C上关于离散分数阶微积分的思想，仍然是最近才兴起的.

虽然关于一致格子x(z)=z和x(z)=qz的离散分数微积分出现和建立相对较晚，但是该领域目前已经做出了大量的工作，且取得了很大的发展[5-8].在最近十年的学术著作中，程金发[9]，Goodrich 和Peterson[10]相继出版了两本有关离散分数阶方程理论、离散分数微积分的著作，其中全面系统地介绍了离散分数微积分的基本定义和基本定理，以及最新的参考资料.有关q−分数阶微积分方面的著作可参见Annaby 和Mansour[11].

非一致格子的定义回溯到超几何型微分方程[12-13]：

的逼近，这里σ(z)和τ(z)分别是至多二阶和一阶多项式，λ是常数.Νikiforov 等[14-15]将式(1)推广到如下最一般的复超几何差分方程

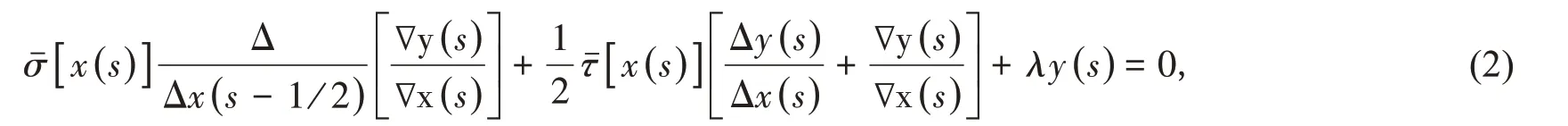
这里(x)和(x)分别是关于x(s)的至多二阶和一阶多项式，λ是常数，Δy(s)=y(s+1)−y(s),∇y(s)=y(s)−y(s−1)，并且x(s)必须是以下非一致格子.

定义1[16-17]两类格子函数x(s)称之为非一致格子，如果它们满足

这里ci,是任意常数，且

当c1=1,c2=c3=0，或c2=1,c1=c3=0或者时，这两种格子函数x(s)：

称之为一致格子.

给定函数F(s)，定义关于xγ(s)的差分或差商算子为

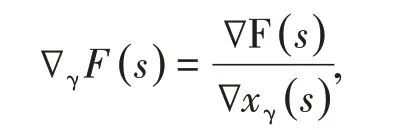
且

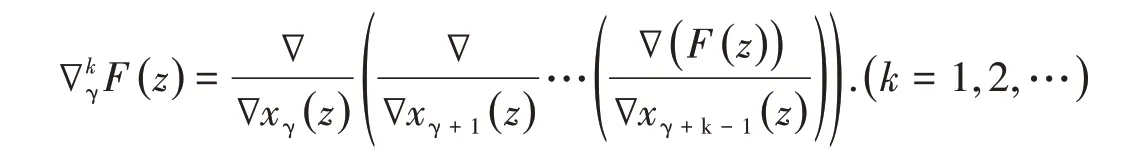
关于差商算子，命题1是常用的.

命题1给定两个复函数f(s),g(s)，成立恒等式

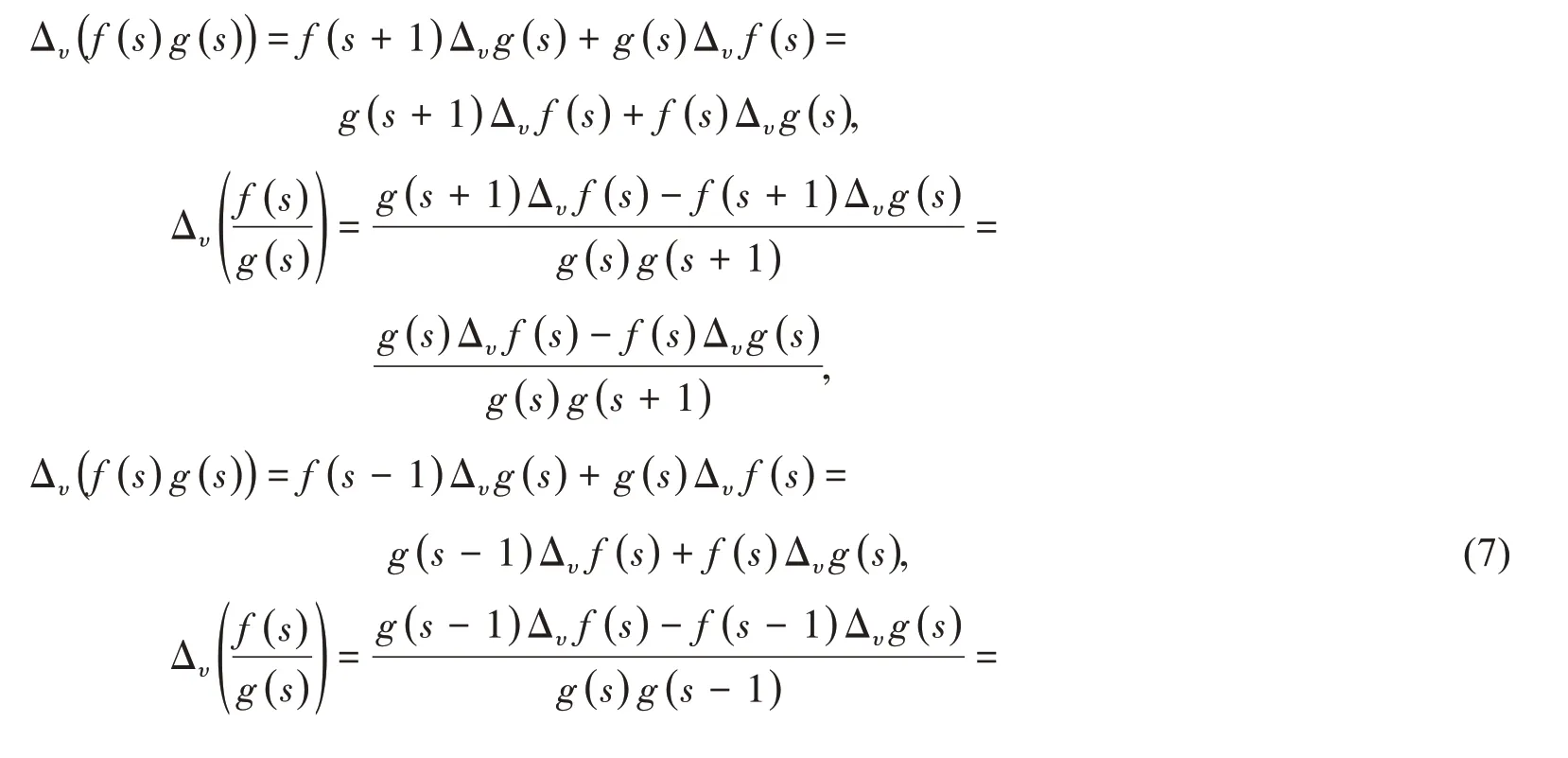
我们必须指出，在非一致格子式(3)或者式(4)，即使当n∈N，如何建立非一致格子的n−差商公式，也是一件很不平凡的工作，因为它是十分复杂的，也是难度很大的.事实上，在文献[14-15]中，Νikiforov等利用插值方法得到了如下n−阶差商∇1(n)[f(s)]公式：

定义2[12-13]对于非一致格子式(3)或式(4)，让n∈N+，那么

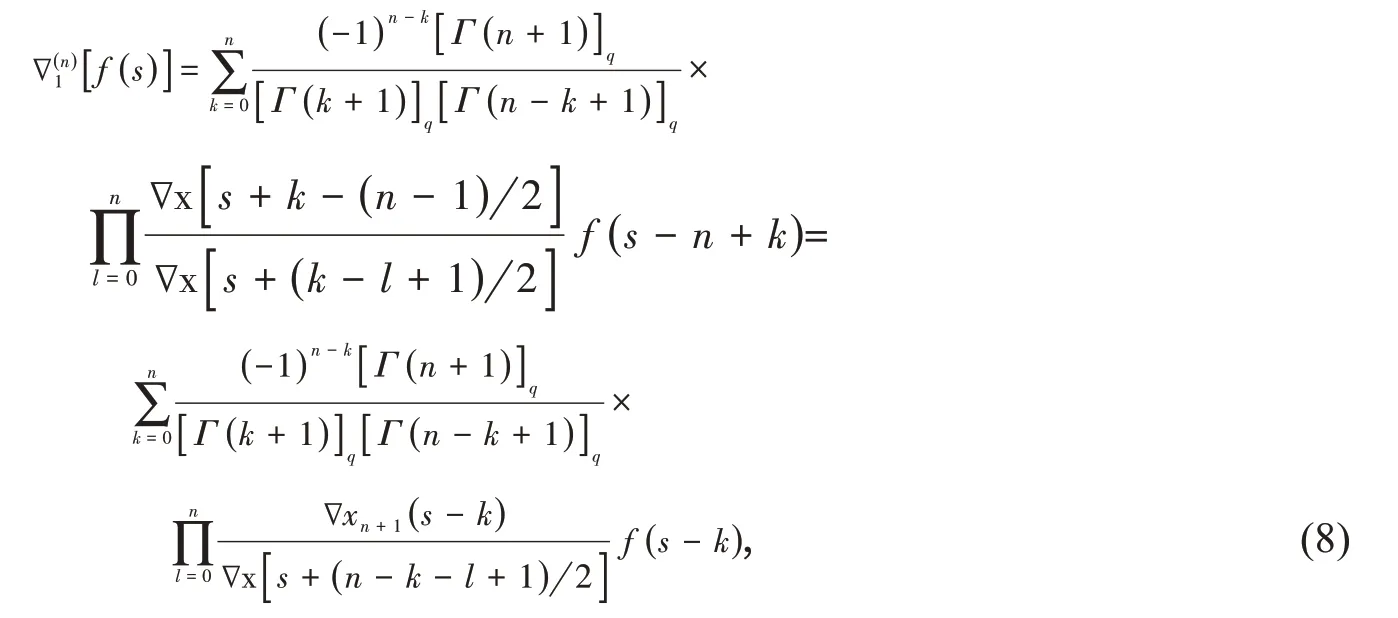
这里[Γ(s)]q是修正的q−Gamma函数，它的定义是

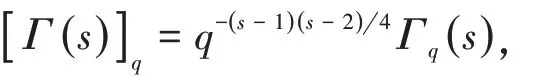
并且函数Γq(s)被称为q−Gamma函数;它是经典Euler Gamma函数Γ(s)的推广.其定义是

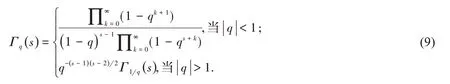
经过进一步化简后，Νikiforov等在文献[14]中将n阶差分∇1(n)[f(s)]的公式重写成下列形式：

定义3[14]对于非一致格子式(3)或式(4)，让n∈N+，那么

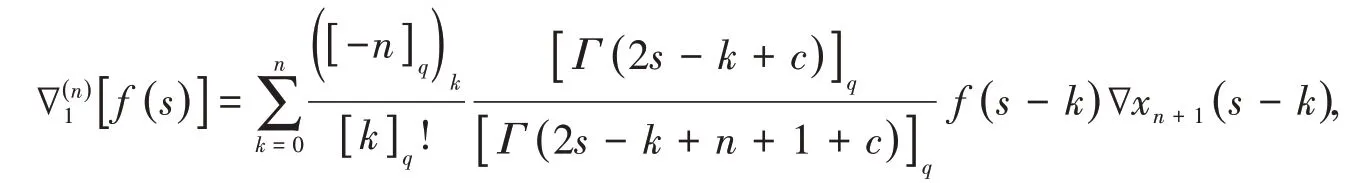
这里

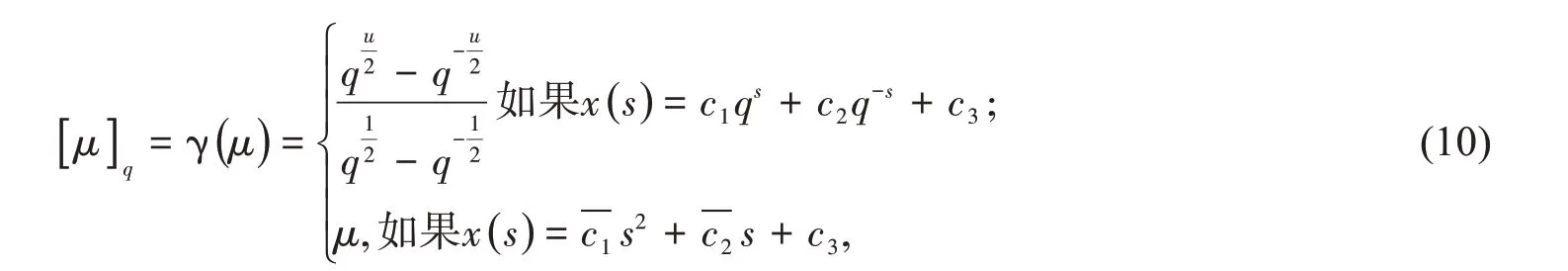
且

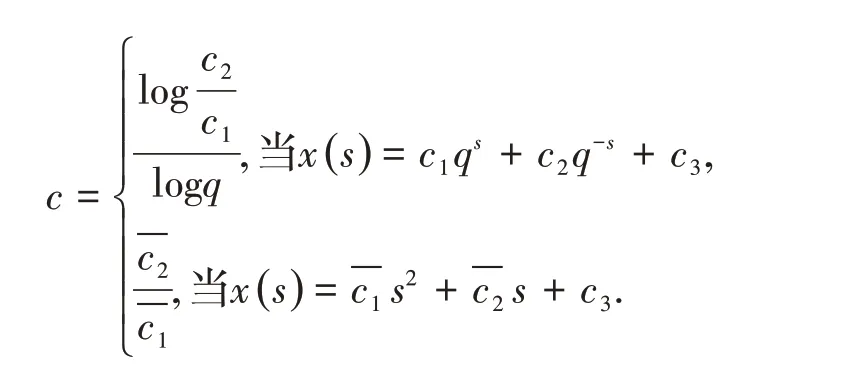
现在存在两个十分重要且具有挑战性的问题需要进一步深入探讨：

1）对于非一致格子上超几何差分方程式（2），在特定条件下存在关于x(s)多项式形式的解，如果用Rodrigues公式表示的话，它含有整数阶高阶差商.一个新的问题是：若该特定条件不满足，那么非一致格子上超几何差分方程式（2）的解就不存在关于x(s)的多项式形式，这样高阶整数阶差商就不再起作用了.此时非一致格子超几何方程的解的表达形式是什么呢？这就需要我们引入一种非一致格子上分数阶差商的新概念和新理论.

因此，关于非一致格子上α−阶分数阶差分及α−阶分数阶和分的定义是一个十分有趣和重要的问题.显而易见，它们肯定是比整数高阶差商更为难以处理的困难问题，自专著[14-15]出版以来，Νikiforov等并没有给出有关α−阶分数阶差分及α−阶分数阶和分的定义，我们能够合理给出非一致格子上分数阶差分与分数阶和分的定义吗?

2)另外，我们认为作为非一致格子上最一般性的离散分数微积分，它们也会有独立的意义，并可以导致许多有意义的结果和新理论.

本文的目的是探讨非一致格子上离散分数阶和差分.受文章篇幅所限，本文我们仅合理给出非一致格上分数阶和分与分数阶差分的基本定义，其它更多结果例如：非一致格子离散分数阶微积分的一些基本定理，如：Euler Beta公式，Cauchy Beta积分公式，Taylor公式、Leibniz公式在非一致格子上的模拟形式，非一致格子上广义Abel方程的解，以及非一致格子上中心分数差分方程的求解，离散分数阶差和分与非一致格子超几何方程之间联系等内容，请参见笔者新专著[16].

2 非一致格子上的整数和分与整数差分

设x(s)是非一致格子，这里s∈ℂ.对任意实数也是一个非一致格子.让∇γF(s)=f(s).那么

选取z,a∈ℂ，和z−a∈N.从s=a+1到z，则有

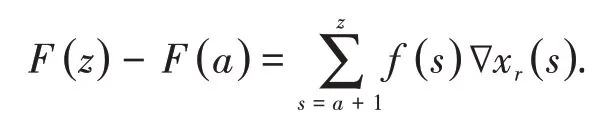
因此，我们定义

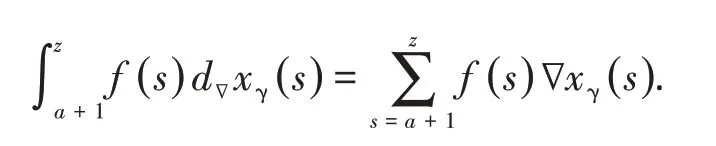
容易直接验证下列式子成立.

命题2给定两个复变函数F(z),f(z)，这里复变量z,a∈C以及z−a∈N，那么成立

现在让我们定义非一致格子上的广义n−阶幂函数[x(s)−x(z)](n)为

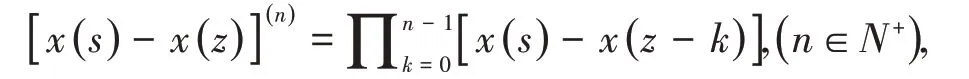
当n不是正整数时，需要将广义幂函数加以进一步推广，它的性质和作用是非常重要的，非一致格子上广义幂函数[xγ(s)−xγ(z)](α)的定义如下：

定义4[17-18]设α∈C，广义幂函数[xγ(s)−xγ(z)](α)定义为

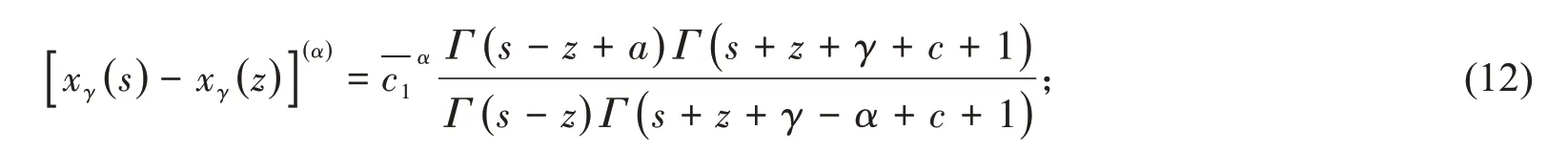
这里Γ(s)是Euler Gamma函数，且Γq(s)是Eulerq−Gamma函数，其定义如式(9).

命题3[17-18]对于x(s)=c1qs+c2q−s+c3或者广义幂满足下列性质：

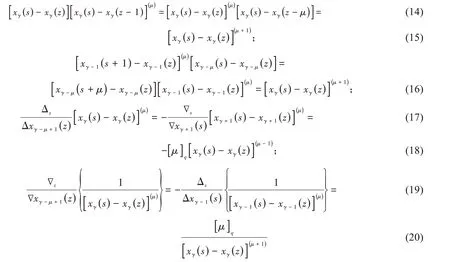
这里[μ]q定义如式（10）.

现在让我们详细给出非一致格子xγ(s)上整数阶和分的定义，这对于我们进一步给出非一致格子xγ(s)上分数阶和分的定义是十分有帮助的.

设γ ∈R，对于非一致格子xγ(s)，数集{a+1,a+2,…,z} 中f(z)的1-阶和分定义为

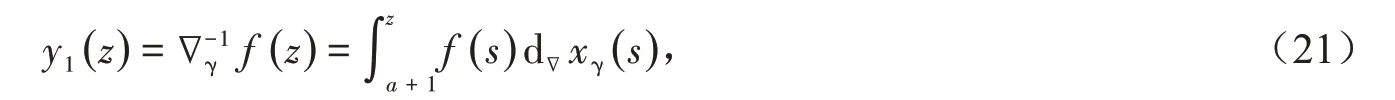
这里y1(z)= ∇−γ1f(z)定义在数集{a+1,mod(1)}中.

那么由命题2，我们有

并且对于非一致格子xγ(s)，数集{a+1,a+2,…,z} 中f(z)的2-阶和分定义为

这里y2(z)= ∇−γ2f(z)定义在数集{a+1,mod(1)}中.

同时，可得

更一般地，由数学归纳法，对于非一致格子xγ(s)，数集{a+1,a+2,…,z} 中函数f(z)，我们可以给出函数f(z)的n−阶和分定义为

这里

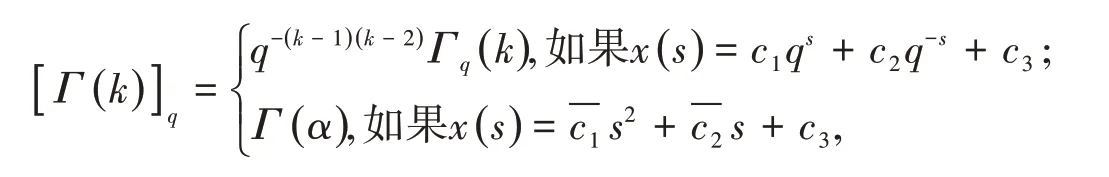
这满足下式

那么成立

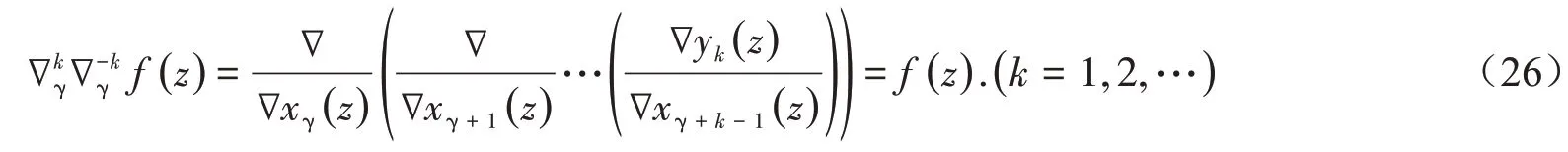
需要指出的是，当k∈C时，式（25）右边仍然是有意义的，因此自然地，我们就可以对非一致格子xγ(s)给出函数f(z)的分数阶和分定义如下：

定义5（非一致格子分数阶和分）对任意Reα∈R+，对于非一致格子式（3）和式（4），数集{a+1,a+2,…,z} 中的函数f(z)，我们定义它的α−阶分数阶和分为

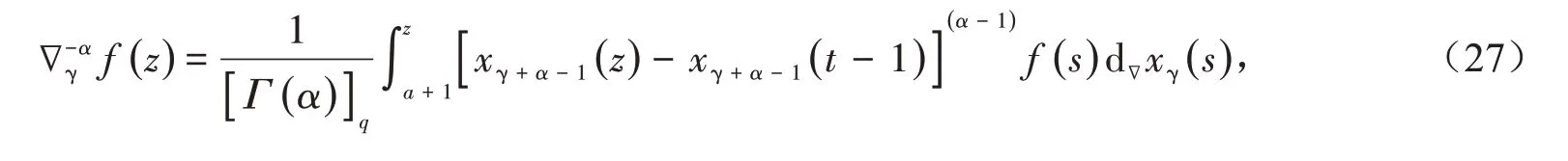
这里

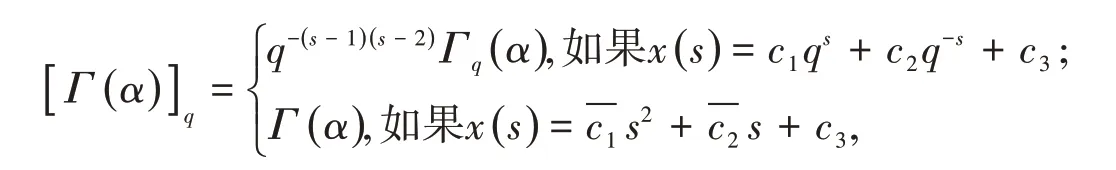
这满足下式

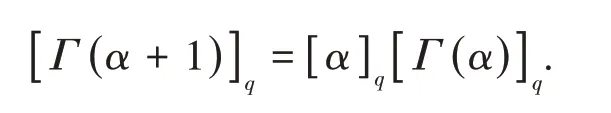
3 非一致格子上的Abel方程及分数阶差分

非一致格子xγ(s)上f(z)的分数阶差分定义相对似乎更困难和复杂一些.我们的思想是起源于非一致格子上广义Abel 方程的求解.具体来说，一个重要的问题是：让m−1 ＜Reα≤m，定义在数集{a+1,a+2,…,z} 的f(z)是一给定函数，定义在数集{a+1,a+2,…,z} 的g(z)是一未知函数，它们满足以下广义Abel方程

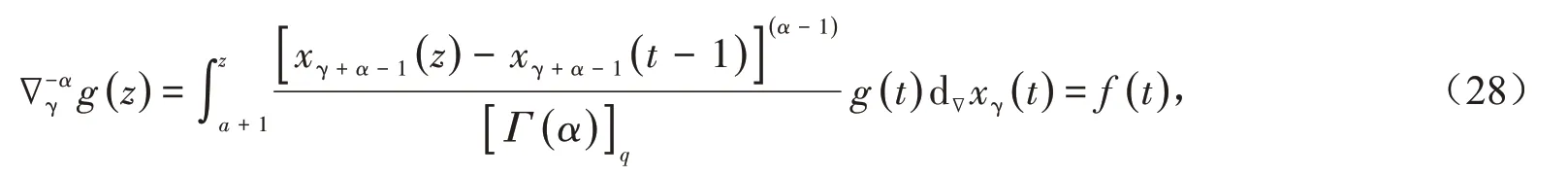
怎样求解该广义Abel方程式（28）？

为了求解方程式（28），我们需要利用重要的Euler Beta公式在非一致格子下的基本模拟.

定理1[16]（非一致格子上Euler Beta公式）对于任何α,β∈C，那么对非一致格子x(s)，我们有

定理2（Abel方程的解）设定义在数集{a+1,mod(1)}中的函数f(z)和函数g(z)满足

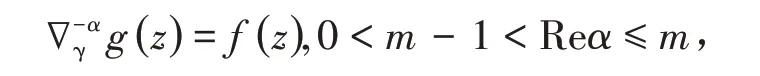
那么

成立.

证明我们仅需证明

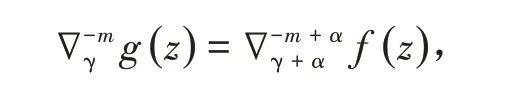
即

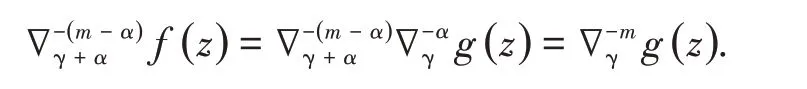
事实上，由定义5可得

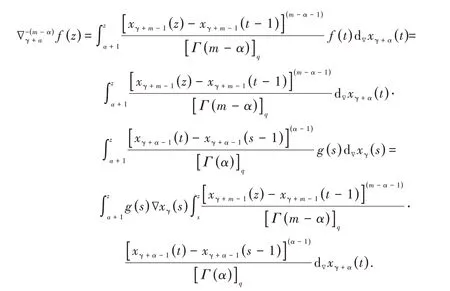
在定理1中，将α+1替换成s；α替换成α−1；β替换成m−α，且将x(t)替换成xγ+α−1(t)，那么xβ(t)替换成xγ+m−1(t)，则我们能够得出下面的等式

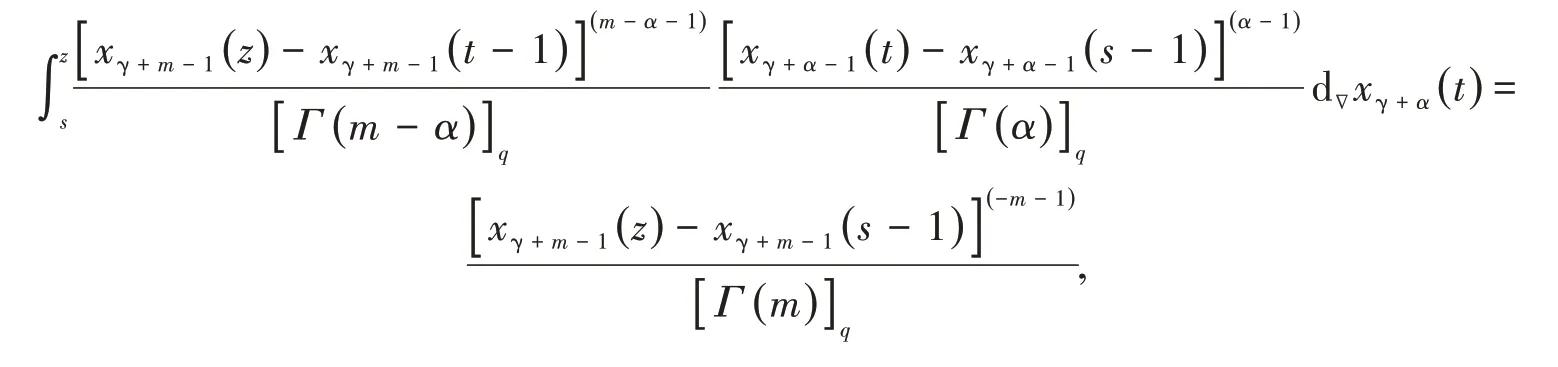
因此，我们有

这样就有

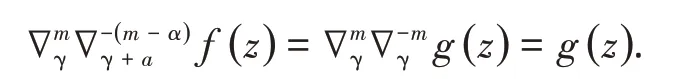
由定理2 得到启示，很自然地我们给出关于f(z)的Riemann-Liouville 型α−阶(0 ＜m−1 ＜Reα≤m)分数阶差分的定义如下：

定义6（Riemann-Liouville 分数阶差分）让m是超过Reα的最小正整数，对于非一致格子xγ(s)，数集{α,mod(1)}中f(z)的Riemann-Liouville型α−阶分数阶差分定义为

形式上来说，在定义5中，如果α替换成−α，那么式（27）的右边将变为

从式（33），我们也可以得到f(z)的Riemann-Liouville型α−阶分数阶差分如下：

定义7（Riemann-Liouville 型分数阶差分2）对任意Reα＞0，对于非一致格子xγ(s)，数集{a+1,a+2,…,z} 中f(z)的Riemann-Liouville型α−阶分数阶差分定义为

将∇γ−α(t)替换成∇γ(t)，那么

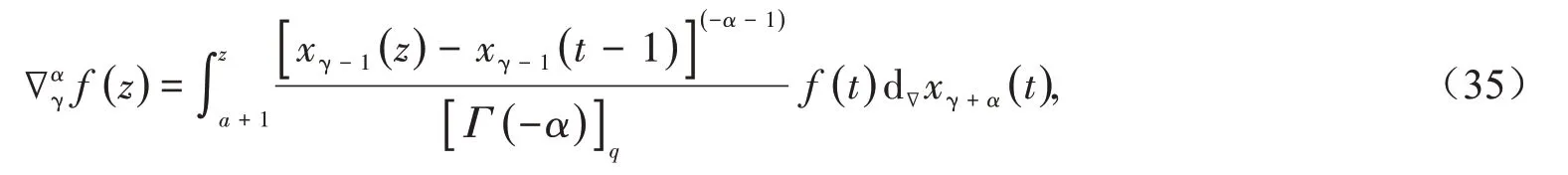
这里假定[Γ(−α)]q≠0.

4 非一致格子上Caputo型分数阶差分

在本节，我们将给出非一致格子上Caputo型分数阶差分的合理定义.

定理3（分部求和公式）给定两个复变函数f(s)，g(s)，那么

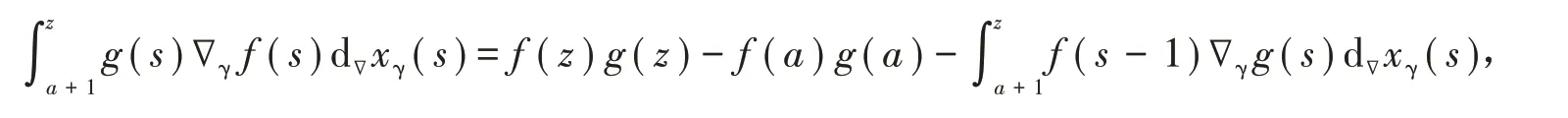
这里z,a∈C，且假定z−a∈N.

证明应用命题1，可得

这样就有

关于变量s，从a+1到z求和，那么可得

与非一致格子上Riemann-Liouville型分数阶差分定义的思想来源一样，对于非一致格子上Caputo型分数阶差分定义思想，也是受启发于非一致格子上广义Abel方程式（28）的解.在本文第3节，借助于非一致格子上的Euler Beta公式，我们已经求出广义Abel方程

是

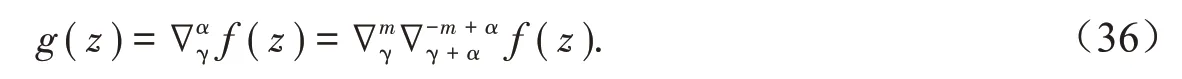
现在我们将用分部求和公式，给出式（36）的另一种新的表达式.事实上，我们有

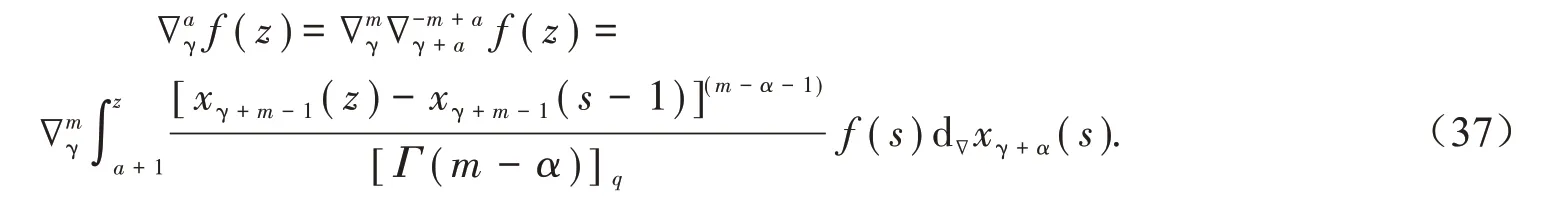
应用恒等式

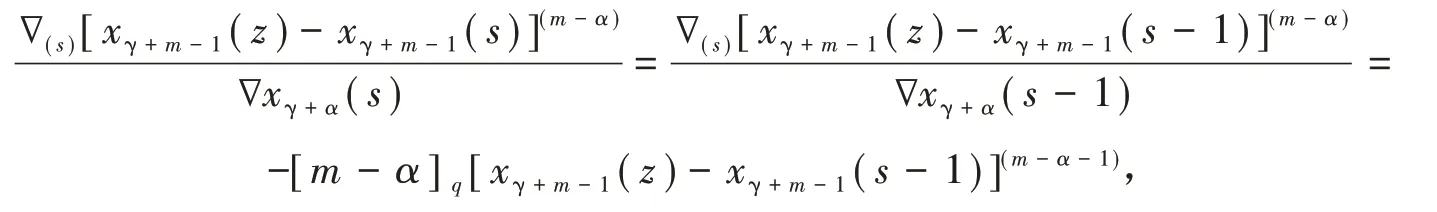
那么以下表达式

可被改写成

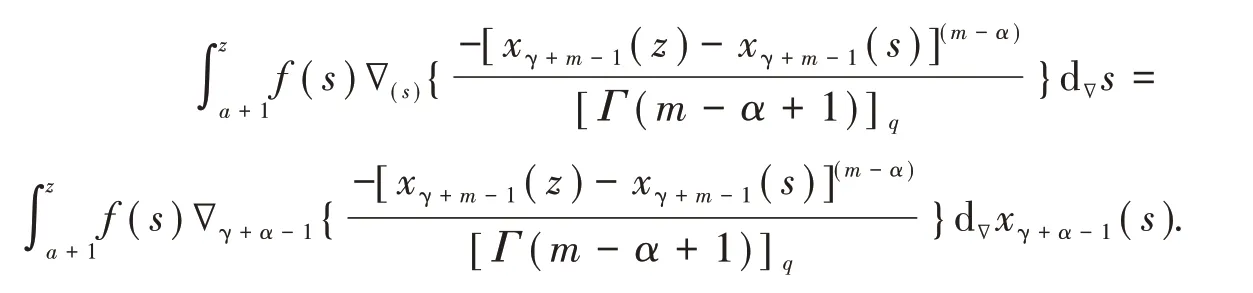
应用分部求和公式，可得

因此，这可导出

进一步，考虑

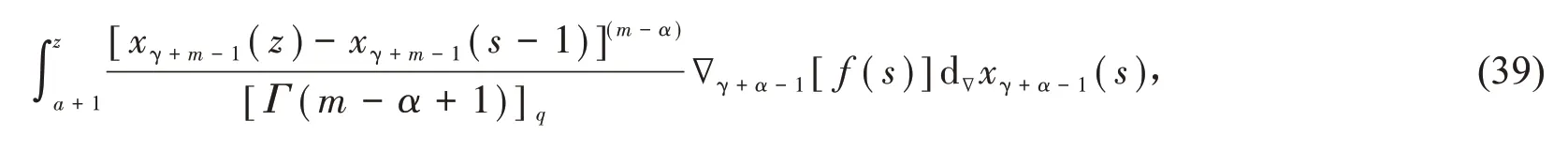
利用恒等式

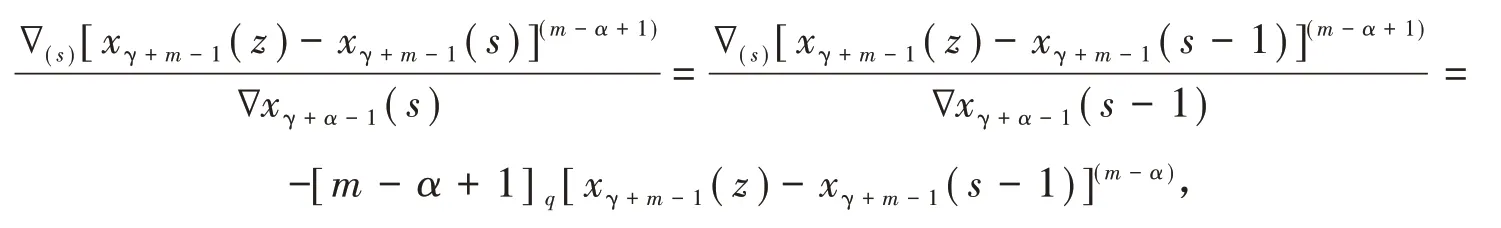
表达式(39)能被改写成

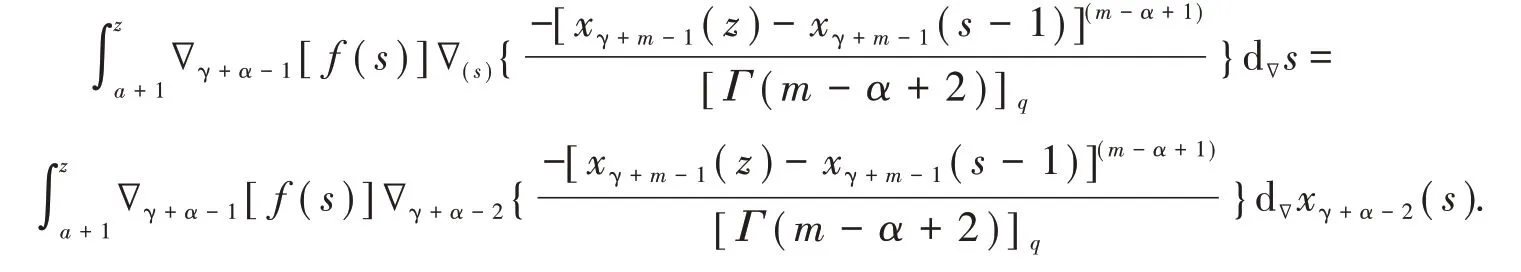
由分部求和公式，我们有

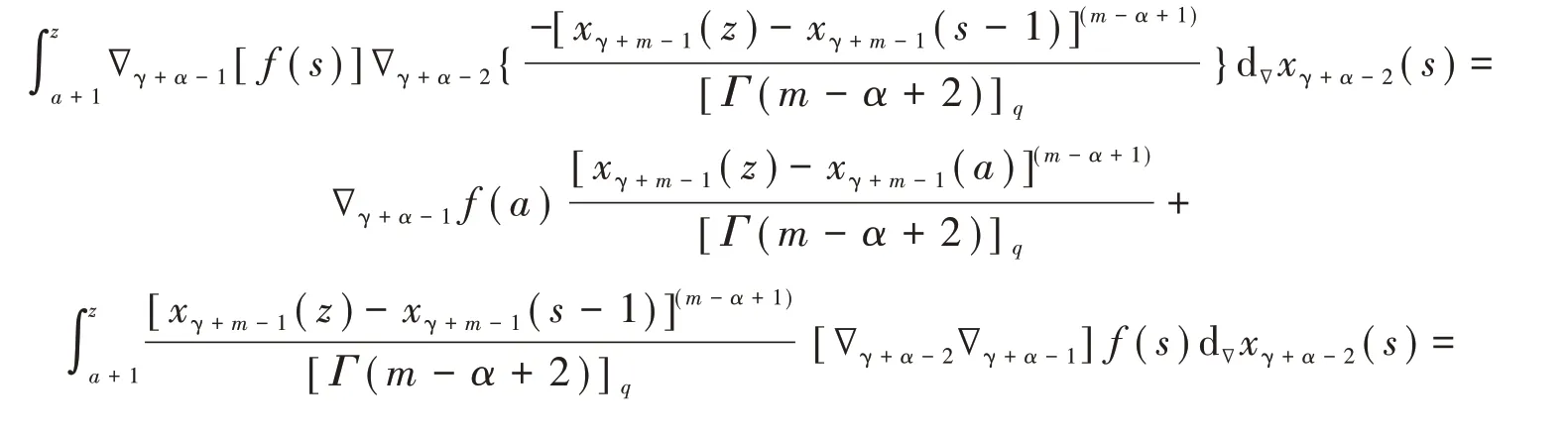
因此，我们得到

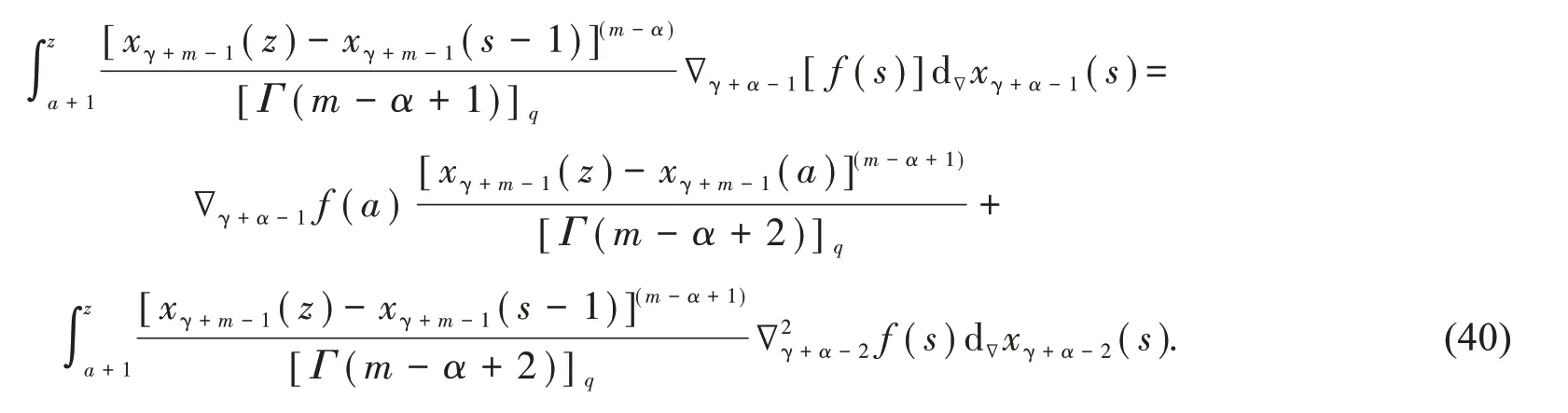
同理，用数学归纳法，我们可得

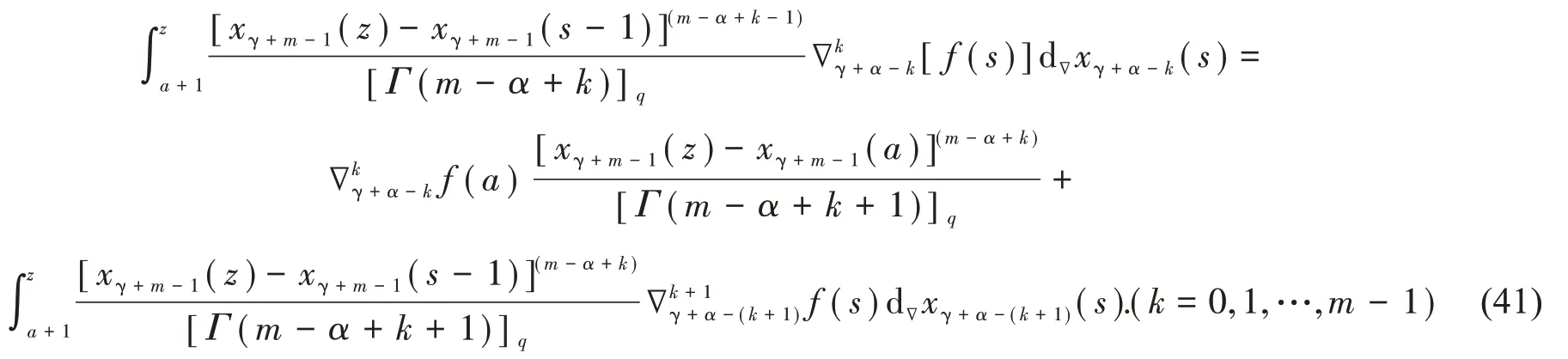
将式（38），（40）和（41）代入式（37），则有

总之，我们有下面的

定理4（广义Abel方程解2）假设定义在数集{a+1,a+2,…,z} 上的函数f(z)和g(z)满足

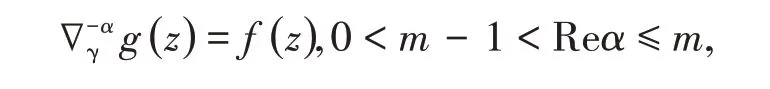
那么

受到定理4的启示，我们很自然地给出函数f(z)的α−阶(0 ＜m−1 ＜Reα≤m)Caputo分数阶差分如下：

定义8（Caputo 分数阶差分）让m是Reα超过的最小整数，非一致格子上定义在数集{a+1,a+2,…,z} 函数f(z)的α−阶Caputo分数阶差分定义为

最后，本文再强调指出：对于非一致格子上超几何差分方程式（2），在特定条件下存在关于x(s)多项式形式的解，如果用Rodrigues公式表示的话，它含有整数阶高阶差分.一个重要的问题是：若该特定条件不满足，那么非一致格子超几何差分方程的解就不存在关于x(s)的多项式形式，这样高阶整数阶差分将不再起作用了，这就迫切需要我们引入一种非一致格子上分数阶差分的新概念和新理论.因此，关于非一致格子上阶分数阶差分及阶分数阶和分的定义是一个十分有趣和重要的问题.有关非一致格子超几何差分方程与离散分数阶差和分的联系，更深入的内容参见笔者著作[16]及文献[19-21].