n-弱幂等完备的n-正合范畴

陈金晶

（闽南师范大学数学与统计学院，福建漳州363000）

为了给出n-丛倾斜子范畴一个公理性的刻画，Jasso 于2016年引入了n-阿贝尔范畴和n-正合范畴的概念[1].n-正合范畴是一类具有n-正合结构的范畴，是经典正合范畴[2-3]的高维推广.n-阿贝尔范畴可看做n-正合范畴，其正合结构为范畴中的所有n-正合列.更多地，Manjra 引入了n-弱幂等完备范畴的概念，并证明了n-弱幂等完备的加法范畴中所有可缩n-正合列构成n-正合结构，故在这个意义下n-弱幂等完备加法范畴是n-正合范畴[4].本文继续研究n-正合范畴与n-弱幂等完备，n-阿贝尔范畴之间的关系，给出了n-正合范畴为n-弱幂等完备的若干等价刻画，并证明了如果n-正合范畴中每个态射均为容许态射，则该范畴是n-阿贝尔范畴.

定义1[1]设d0X:X0→X1为中态射，称如下态射列为d0X的n-余核，

如果对任意的1 ≤k≤n−1，dkX是dkX−1的弱余核，且dnX是dnX−1的余核.一个态射的n-核的概念是对偶的.

构成的满子范畴.Jasso[1]引入了加法范畴中n-推出、n-正合列的定义.

定义2[1]1)设为Chn−1()中的复形，a0:X0→Y0是中态射.称复形态射a:X→Y为复形X沿着a0的一个n-推出，

图1 n-推出Fig.1 n-push out

如果在a的映射锥C(a):

特别地，

对偶地有n-拉回的定义.

2)称Chn()中复形

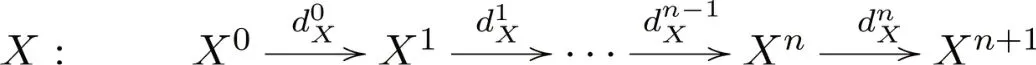
为n-正合列，如果(d0X,…,dnX−1)是dnX的n-核且(d1X,…,dnX)是d0X的n-余核.

3)设X,Y为中n-正合列.称复形态射f:X→Y为弱同构，如果存在k∈{0,1,…,n+1}使得f k与fk+1是同构，其中规定n+2:=0.

性质1[1]设g0:X0→Z0为中态射.已知f:X→Y为X∈Chn−1()沿着g0的n-推出，如图2所示.

图2 X沿着g0的n-推出Fig.2 The n-push out of X along g0

图3 复形态射Fig.3 The morphism of complexes

称X∈Ch()是可缩复形，如果1X同伦于0X.下面关于可缩复形的性质是重要的.

性质2[1]设是加法范畴，X是Chn()中复形且(d1X,…,dnX)是d0X的n-余核.则d0X是可裂单当且仅当X是可缩n-正合列.

定义3[1]给定正整数n及加法范畴M.设是中n-正合列组成的一个类，称为中一个n-正合结构，如果中对象在弱同构下是封闭的，且满足以下公理：

E1op)所有-容许满态射构成的类在合成下是封闭的.

图4 X沿着f0的n-推出Fig.4 The n-push out of X along f0

E2op)对任意-容许n-正合列X及态射gn+1:Yn+1→Xn+1，存在X沿着gn+1的n-拉回使得dnY为-容许满，即有如下交换图5：

图5 X沿着gn+1的n-拉回Fig.5 The n-pull back of X along gn+1

性质3[1]令（，）为n-正合范畴，则

1)Ch（n）中可缩复形是容许n-正合列;

2)设在下列交换图6中，若第二行为容许n-正合列且(d1X,…,dnX)是d0X的n-余核，则交换图中第一行也是容许n-正合列.

图6 交换图Fig.6 The commutative diagram

定义4[4]加法范畴称为n-弱幂等完备的，如果中每个可裂单态射具有n-余核且每个可裂满态射具有n-核.当n=1时，称为弱幂等完备范畴.

Manjra[4]证明了n-弱幂等完备范畴是n-正合范畴，其正合结构是范畴中的所有可缩n-正合列.下面是本文的第一个主要结果，给出了n-正合范畴是n-弱幂等完备的若干等价刻画.该结果推广了文献[3]中关于弱幂等完备的正合范畴的等价刻画.

定理1设是n-正合范畴，则下列叙述是等价的：

2)每个可裂单态射是容许单，每个可裂满态射是容许满.

3)若态射gf是容许满，则g是容许满;若gf是容许单，则f是容许单.

4)若态射gf与f都是容许满，则g是容许满;若gf与g都是容许单，则f是容许单.

证明1)2)：设f0是可裂单态射，因为是n-弱幂等完备范畴，f0具有n-余核(f1,…,f n).根据性质2可知

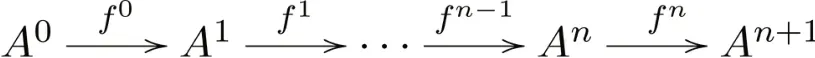
是可缩n-正合列.注意到可缩n-正合列是容许n-正合列，故f0是容许单.利用性质2的对偶可知每个可裂满态射是容许满.

图7 X沿着f的n-推出Fig.7 The n-push out of X along f

其中第一行为容许n-正合列.利用性质1，进一步可诱导出中对应于s:X→Y的好n-推出进而对于如下复形态射t:X→Z，

图8 复形态射Fig.8 The morphism of complexes

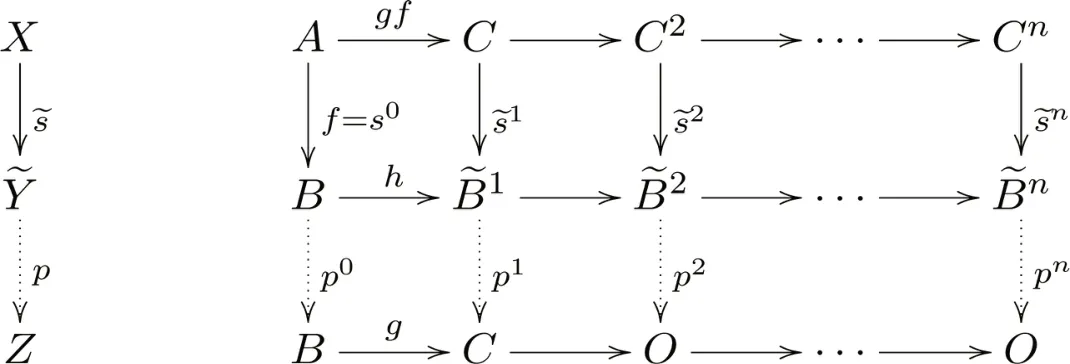
图9 好n-推出的泛性质Fig.9 The universal property of good n–push out

下面证明l1h是f的弱余核.首先设态射k:B→K使得kf=0，则根据好n-推出的泛性质，存在交换图10，

图10 好n-推出的泛性质Fig.10 The universal property of good n–push out

使得q0=1B，q1=0.由于l1是的弱余核，存在m:D2→K使得ml1=q1.进而k=q1h=m(l1h).所以l1h是f的弱余核.又注意到对任意的2 ≤i≤n−1，li是li−1的弱余核且ln是ln−1的余核，故f有n-余核(l1h,l2,…,ln).已知gf是容许单，故可诱导出复形态射

图11 n–余核的泛性质Fig.11 The universal property of n-cokernel

根据性质3可知(f,l1h,l2,…,ln)为容许n-正合列，即f是容许单.

n-阿贝尔范畴是一类具有特殊性质的n-正合范畴，是经典阿贝尔范畴[5]的高维推广.n-阿贝尔范畴的定义是Jasso于2006年如下引入的.

定义5[1]令n为固定正整数.称加法范畴为n-阿贝尔范畴，如果满足以下公理：

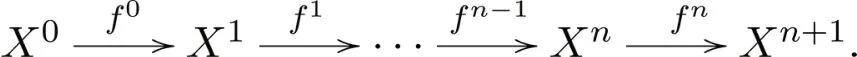
A2op)对于中任意满射gn:Xn→Xn+1，存在n-正合列

n-阿贝尔范畴自然地看做为n-正合范畴，其正合结构为该范畴中所有的n-正合列.本文以下考察了n-正合范畴满足何条件时是n-阿贝尔范畴.为此首先引入n-正合范畴中容许态射的概念.

定义6设是n-正合范畴，f:A→B为范畴中态射.如果f可分解为f=rs使得s为容许满态射，r为容许单态射，则称f为中容许态射.

定理2设为n-正合范畴.如果中每个态射均为容许态射，则是n-阿贝尔范畴.

证明只需验证满足定义5中4条公理即可：

A0)设e:A→A为中幂等态射，即e2=e.根据e为容许态射，有以下分解e=rs，其中s:A→B为容许满，r:B→A为容许单.则(rs)(rs)=e2=e=rs.注意到s为满射，r为单射，故sr=1B.这表明了是幂等完备范畴;

A1)设f:A→B为中态射且f分解为f=rs，其中s为容许满，r为容许单.由于s是容许满，在中s有n-核，记为

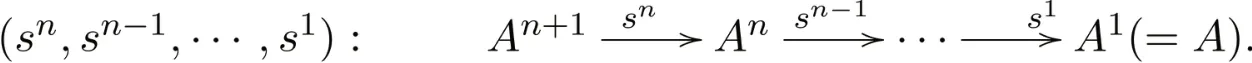
则对于1 ≤i≤n−2，si+1是si的弱核，且sn是sn−1的核.注意到s1是s的弱核且r为单射，易知s1是f=rs的弱核.综上，(sn,sn−1,…,s1)是f的n-核.对偶分析可知f也具有n-余核;

A2)设f0为中单射.已知f0可分解为f0=rs，其中r为容许单，s为容许满.则中存在n-正合列(r,r1,r2,…,rn)与(sn,…,s2,s1,s).注意到f0s1=r(ss1)= 0，故s1=0.进而s=cokers1为单位态射.故(f0,r1,r2,…,rn)为n-正合列，条件A2)成立.对偶分析可知条件A2op亦成立.

注1事实上当n=1时，定理2推广了Freyd[6]的一个经典结果：如果是正合范畴且其中每个态射均为容许态射，则是阿贝尔范畴.