质量监测背景下一道毕业试题引发的思考

辛家宝

摘  要：核心素养要求培养学生的创新能力和实践能力，促进知识的动态生成。在探究多边形内角和时，“如何探究”这个问题值得我们去研究，去思考，去分析。我们可以从特殊的四边形想起，可以利用转化的策略去思考，也可以巧用几何画板动态演示，这几种方法都可以把不规则的四边形转化为若干个三角形，从而探究出多边形的内角和。

关键词：创新、转化、思考。

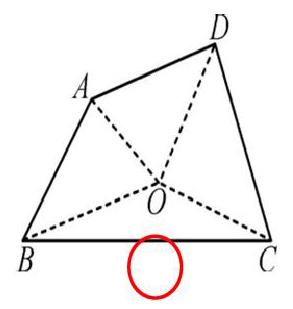
2020年沛县六年级毕业质量监测倒数第3题：在探索四边形ABCD的内角和时，聪聪采用如图所示的转化方法，他是怎样推算的？请写出算式。（如右图）：

答：四边形ABCD分成了4个三角形，每个三角形的内角和是180°，共180°×4=720°但中间的4个角不属于四边形，因此四边形的内角和是720°-360°=360°

命题者注重了学生思维融合能力的考查，学生根据问题的导向，充分挖掘知识的潜在因素，在经历探究的过程中，明确了四边形内角和是360°的知识形成过程，重点培养其推理能力和迁移能力。近期，沛县实验小学教育集团也围绕以“六年级质量监测背景下的数学命题研究”为课题，开展了一系列的主题教研活动。活动中力求揭示命题背后所隐藏的知识和技能，理清知识的来龙去脉，梳理知识之间的关联，明确知识在结构中的地位。试题即要考查学生的知识技能又要考查学生的数学素养，这就要求我们在命题设计中依据课标，基于教材，外显思维的教育方式来开展主题活动，首先要对教材认真分析、深入挖掘，精心设计来整合资源。一份好的试卷要能真正的检测出学生的素养水平，不但要重视知识和技能的掌握，更要重视思维的过程和知识的迁移能力，深入考査学生的思维深度和数学素养。小学数学核心素养要求：培养学生的创新能力和实践能力，促进知识的动态生成。在探究多边形内角和时，一般用分割法，将不规则的多边形分割成若干个三角形来探究，利用三角形的内角和是180°来解决问题，在探究多边形内角和的过程中是否还有其它的方法呢？这个问题值得我们去研究，去思考，去探索。

一、巧用特殊图形，探究内角和。

教学时，可以从长方形、正方形、平行四边形、梯形等特殊的四边形入手来探究四边形的内角和。因为长方形和正方形的每个内角都是90°，所以四边形的内角和都是90°×4=360°，教師引导学生先猜测并验证其它的四边形内角和是否也是360°呢？有经验的教师在教学时都要给孩子们留下大量的时间来探究，通过量一量、拼一拼等大量的操作活动来验证四边形的内角和都是360°这个结论，形成简单的建模思想。

二.巧用转化策略，探究内角和。

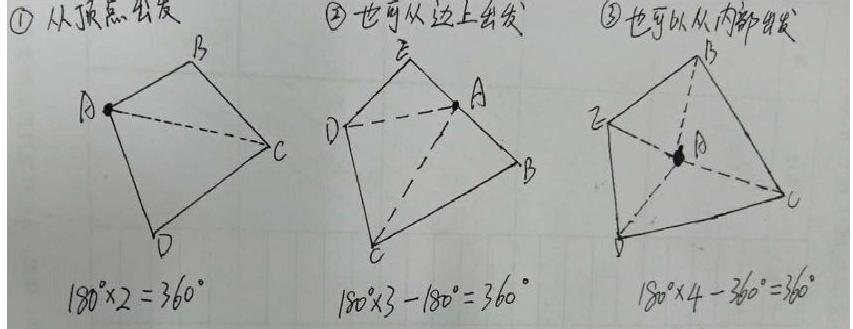
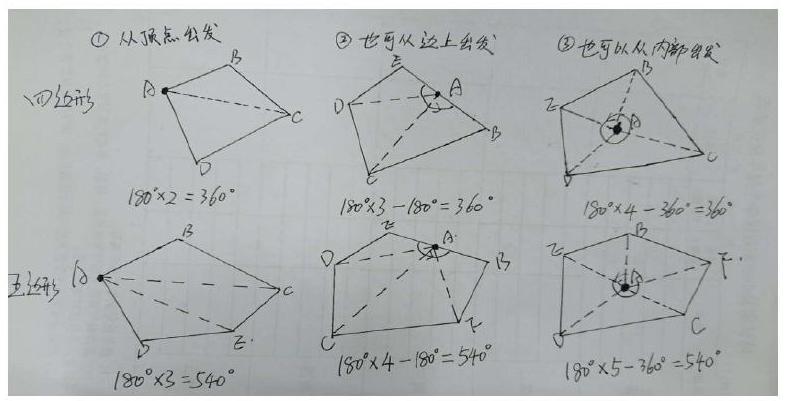
转化是一种数学思想更是一种解决问题的策略。教学时利用转化的策略，可以把不规则的四边形转化为若干个三角形来探究四边形的内角和。教师引导孩子们可以从顶点分成两个三角形（如1图）;也可以从任意一条边上的任意一点出发分成三个三角形（如2图，注意要减去多出的一个平角）;也可以从内部一点出发，把四边形分成四个三角形来探究。（如图3，要减去内部一个周角）。

孩子们借助四边形内角和的方法，利用知识的迁移教师再引导孩子们继续探索五边形、六边形、n边形，学生借助图形，在合作中探究出三角形的个数与多边形内角和之间的关系，求出多边形的内角和公式，在引导探究的过程中教师应多创造机会，给孩子们留下大量的时间，通过猜想，大胆假设，合作交流，动手操作中得出结论，教学时让孩子们注重知识的形成过程和应用过程，鼓励孩子们大胆参与，让学生真正的动起来，在活动体验中感受和验证从而得出结论，体验成功的快乐。教师在引导探究的过程中不但培养了学生应用知识的能力，而且还培养了学生的创新意识。体会到了转化的数学策略，初步建立模型，从而有效的解决了问题。（如图）

三、巧用几何画板，探究内角和。

教学中巧妙的运用几何画板绘图软件就能很好的解决这个问题，它能把问题通过绘图软件设计成动态模拟的形式呈现出来，制作的课件不仅形象而且还很生动，能有效的帮助学生解决很多复杂、抽象的问题，从而明白数量之间的关系，几何画板绘图软件能将每一种四边形的内角和的验证过程演示的清晰而形象，轻松顺利的突出了重点、突破了难点，帮助孩子们更好的理解四边形的内角和为什么是360°，从四边形推广到五边形、六边形等等，得出n边形内角和的计算方法。

在数学探究活动中，让学生亲身体验在转化的过程中探究规律本质，沟通知识间内在联系，体会建模思想。STEM教育理论也认为，数学策略的学习其乐趣不在于形式和结果，而在于内涵和过程，在过程中建构、体会、感悟、累积，慢慢地探究出数学的本质和价值。

参考文献：

[1]《中小学数学》2020.9（上旬）

[2]郑毓信：以深度教学落实数学核心素养（小学数学教师）2017

（江苏省徐州市沛县实验小学）