基于广义多项式混沌的跨座式单轨车辆随机平稳性分析

周生通，王 迪，肖 乾，李鸿光，张 沛

(1.华东交通大学 载运工具与装备教育部重点实验室，南昌 330013；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

自我国第一条跨座式单轨交通线路在重庆市建成以来，跨座式单轨凭借其独特优势和特点，已成为我国城市轨道交通系统首选制式之一，而与之相关的跨座式单轨车辆动力学性能研究在近年来也受到了国内外学者的普遍关注[1]。众所周知，动力学性能的好坏决定着轨道车辆运行品质的高低，一直以来国内外学者主要从车辆结构参数、轮轨接触特性和外部环境条件等研究不同因素对轨道车辆动力学性能的影响[2-4]。但现有研究大多是建立在确定性分析框架下的，即建立确定的动力学仿真模型，设置固定的参数，时域积分得到车辆系统动态响应，而且在探讨参数变化对系统响应的影响规律时，还往往存在选取参数变量单一、仿真工况有限等问题，得到的响应规律较为片面。然而，若是执行完全参数分析又会使仿真组合工况过于庞大，难以完成[5]。另一方面，在工程实践中，轨道车辆系统的悬挂参数(如刚度和阻尼系数)、轨道和轮轨参数(如轨道超高率、轮轨静/动摩擦因数)、车辆载重等往往会受运营里程、制造/安装误差、磨损老化、外部环境(如温度、湿度)等的影响而变化，再加之各种偶然和认知方面的影响因素，势必造成车辆参数具有随机不确定性[5-7]。显然，这些随机因素在传统确定性分析中是无法被合理考虑的，进而也就无法准确预测轨道车辆动力学性能。因而，针对跨座式单轨车辆系统，发展有效的随机分析方法，开展随机参数作用下的车辆动力学研究，就显得很有必要。

当前，针对跨座式单轨车辆的随机分析并不多见，已有研究主要是一些其他类型的轨道列车。早期的轨道车辆随机分析主要关注轨道不平顺作用下的随机响应问题，利用随机振动的线性频域法、数值积分法、Monte Carlo仿真、虚拟激励法和概率密度演化法等方法求解[8-9]。近年来，随着随机量化理论的发展，考虑随机参数的轨道车辆动力学性能开始受到关注，如Kassa等[6]考虑轴重、轮轨摩擦因数和轮轨型面的随机性，分析了某列车-道岔耦合系统的随机动力响应；滕万秀等[7]考虑车辆系统悬挂参数、轮轨匹配、轮轨界面参数的随机性，研究了高寒动车组低温环境运行时的动力学性能；罗仁等[5,10]考虑悬挂刚度和阻尼、轮轨匹配参数、轮轨界面参数、载荷工况和轨道不平顺的随机统计分布，获得了高速列车动态包络线和动力学指标的统计规律；Bigoni等[11]研究了随机悬挂参数下的轨道车辆临界转速全局灵敏度；赵岩等[12]研究了轨道不平顺和一系和二系弹簧刚度随机下的车轨耦合系统振动灵敏度问题；李双等[13]则假设悬挂阻尼器两端橡胶节点刚度服从高斯分布，获得了Sperling指标的统计矩和灵敏度。不过，这些已有研究多是基于仿真工况随机组合思想利用Monte Carlo仿真或拉丁超立方抽样(Latin hypercube sampling,LHS)方法进行分析的。显然，对于具有高昂计算成本的复杂非线性轨道车辆数值仿真模型，大样本的组合工况计算是不现实的，而在有限样本数目限制下，即使是适合于小样本工况的LHS方法有时也难以获得满足精度的结果，尤其是在高阶统计矩和概率分布方面。

在轨道车辆多目标优化领域，构建近似模型(亦称代理模型)是克服车辆仿真模型高昂计算成本的主要途径，如谢欢等[14]结合Kriging模型、二阶响应面、径向基函数模型构造混合代理模型，研究悬挂参数的多目标优化问题；东方世平[15]利用有限实验设计样本构造悬挂系统参数与动力学指标的径向基函数人工神经网络模型，实现CRH2型动车组悬挂参数的快速多目标优化。作为一类随机代理模型，非侵入式广义多项式混沌(generalized polynomial chaos,gPC)方法在随机不确定量化领域被广泛应用[16-18]，其本质是通过对随机响应量进行有限的多项式混沌展开，从而实现对复杂非线性数值模型随机响应的高效估算。Bigoni等[19]利用随机配置法和gPC方法研究了某简单Cooperrider车辆模型的非线性临界转速统计分布规律；项盼等[20]则结合虚拟激励法和gPC方法开展了车轨耦合系统的复合随机振动分析，指出gPC方法存在的维数灾难问题，并讨论了一种结合继承性拉丁超立方抽样和利用决定系数筛选基函数的自适应方案。当前，针对gPC的自适应稀疏展开技术颇受重视并发展迅速，如逐步回归[21]、最小角回归[18,22]、压缩感知[23]等。其中，最小角回归算法利用相关性选出对模型响应影响大的回归量以形成最佳基函数集合，是一种非常有效的自适应稀疏gPC展开方案。

为此，本文以某型跨座式单轨车辆为研究对象，首先构建随机参数作用下的单轨车辆随机平稳性分析模型；之后，考虑到单轨车辆数值仿真模型的高昂计算成本，同时在有限试验设计样本限制下，探讨广义多项式混沌的自适应稀疏展开方案；最后，结合工程算例分别基于拉丁超立方抽样法和广义多项式混沌法，开展不同速度等级下单轨车辆随机平稳性指标的统计分布规律和全局灵敏度分析，对比两种方法结果的异同，验证自适应稀疏gPC方法的有效性。

1 跨座式单轨车辆的随机平稳性模型

1.1 参数化UM仿真模型建立

图1所示为某型跨座式单轨车辆，由1个车体和2个转向架子系统构成，其中单个转向架子系统包括1个构架、4个走行轮、4个导向轮和2个稳定轮，属于典型的多体动力学系统。为此，这里利用UM(universal mechanism)多体动力学软件的参数化建模功能，建立单轨车辆输入参数、运行速度与系统加速度响应之间的映射模型

图1 跨座式单轨车辆参数化UM仿真模型Fig.1 Parameterized UM simulation model of straddle monorail vehicle

(1)

在UM多体动力学仿真模型中，将车体、转向架构架及各轮组假设为刚性体，并用铰接和力元模拟各刚体之间的连接关系，其中采用基于Fiala模型的轮胎特殊力元(tyre)模拟各轮组的橡胶轮胎，以黏弹性的空间线性力元(viscous-elastic)模拟车体与构架之间的空气弹簧，以点绘式双极力元(point-numberic)模拟构架与车体之间的减振器，以衬套特殊力元(bushing)模拟牵引拉杆、抗侧滚扭杆和横向止挡等的刚度阻尼特性，最终建立的跨座式单轨车辆的UM仿真模型共有38个自由度，如表1所示。

表1 跨座式单轨车辆仿真模型自由度Tab.1 Degree of freedom of straddle monorail vehicle model

1.2 单轨车辆平稳性指标

车辆运行平稳性是考虑车辆在直线或曲线工况下运行状态的描述，是对旅客乘坐舒适性和运载货物完整性的评价。当前，单轨车辆的运行平稳性多是依据轨道车辆客车运行平稳性指标进行评价。为此，将式(1)中加速度响应量a(t)取为基于UM仿真模型获得的距离1位心盘一侧1 000 mm的车体地板面上的加速度时间历程，那么参照GB/T 5599—1985，单轨车辆的运行平稳性指标Y可由下式计算

(2)

(3)

式中：fi(i= 1,2,…,n)为加速度时间历程a(t)进行频谱分析后在频域中的第i个频率分量，Hz；Wi为频率为fi时的平稳性指标分量；Ai为频率为fi时的振动加速度幅值，g；F(fi)为频率为fi时的频率修正系数，由GB/T 5599—1985确定。

若测量的加速度响应a(t)为垂向加速度历程，则式(2)计算的是垂向平稳性指标，若是横向加速度历程，则计算的是横向平稳性指标。

1.3 随机平稳性分析模型

依据不确定性传播原理，当考虑输入向量X的随机不确定性时，单轨车辆动力学系统响应量a(t)也必然是随机的，进而计算的平稳性指标Y将呈现随机分布规律。为此，在前述确定性平稳性指标分析基础上，将输入向量X作为随机向量，可建立描述单轨车辆不同速度等级V下的随机平稳性分析模型

(4)

单轨车辆运行平稳性指标是利用车体上规定位置的各方向振动加速度经统计处理后得到的评价车体随机振动的指标。显然，在众多影响平稳性指标的系统定义参数中，各参数的随机性对平稳性指标的影响程度是不同的。这里，参照已有研究工作[24]，选取部分关键的单轨车辆外部运行条件及自身结构参数作为系统输入参数，组成随机输入向量X，并研究各参数随机性作用下的单轨车辆运行平稳性随机分布和响应灵敏度规律。具体包括：①车辆载重m；②悬挂元件刚度阻尼参数——走行轮垂向刚度k1、水平轮(包括导向轮和稳定轮)径向刚度k2、空气弹簧垂向刚度kz和横向刚度kxy、抗侧滚扭杆刚度CAX、牵引拉杆刚度CX、空气弹簧垂向阻尼cz；③轨道和轮轨界面参数——轨道超高率h、轮轨动摩擦因数μ1和轮轨静摩擦因数μ0。将各参数组成随机向量X，即

X=[m,k1,k2,kz,kxy,CAX,CX,cz,h,μ1,μ0]T

(5)

2 自适应稀疏广义多项式混沌法

2.1 平稳性指标的gPC近似

依据gPC展开理论，设M维随机向量X各元素独立且满足Askey方案，否则必须利用随机空间变换方法变换实现[16,18]。那么，具有有限方差的随机平稳性指标Y可被近似展开为

(6)

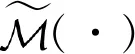
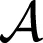
(7)

式中：‖·‖1为1范数；p为gPC最大展开阶数。在标准截断下，总的gPC展开项数P为

(8)

若gPC基函数是标准正交的，那么随机平稳性指标Y的均值μ和方差D(或标准差σ)可由gPC展开系数直接估算，即

(9)

(10)

对于随机平稳性指标Y的更高阶统计矩(如偏斜度、峰度)、概率分布等信息可由大量Monte Carlo样本在gPC近似模型式(6)的基础上统计推断获得。此外，利用gPC展开系数还可直接获得随机平稳性指标对各随机变量的Sobol全局灵敏度[18,25]。其中，一阶Sobol灵敏度指标为

(11)

式中，集合Ii={α∈|αk≠0⟺k=i}。Si描述了单一随机变量Xi(i=1,2,…,M)对随机响应方差D的相对贡献大小。总的Sobol灵敏度指标为

(12)

2.2 自适应稀疏展开方案

从式(8)中可以看到，随着维数M和阶数p的增加，总的gPC展开项数P(即随机模型维数)将急剧增加，从而导致随机平稳性分析的维数灾难问题。因此，考虑到跨座式单轨车辆UM仿真模型的高昂计算量，在有限试验设计样本的限制下，提出有效的降维方法，以获得最佳gPC近似精度，就显得尤为重要。

通常，增加阶数p会提高gPC模型的近似精度，但阶数的增加也意味着随机维度P的大幅增加，尤其是维数M较大时(文中M= 11)，同时在有限样本数据下，过高的维度(如P接近甚至超过N)将会造成过拟合问题，甚至无法求解。为此，这里给出结合低阶交互截断、最小角回归(least angle regression,LAR)、最小二乘法(ordinary least squares,OLS)和留一法交叉验证(leave-one-out,LOO)实现的gPC自适应稀疏展开方案，如图2所示。可以看到，在N个有限试验设计数据基础上，该方案主要从两个方面：①gPC最大展开阶数p的自适应选取；②特定展开阶数下的基于低阶交互截断和LAR的最优稀疏gPC基集合*(p)选取，来实现gPC近似模型的降维和获得最佳近似精度的。

图2 广义多项式混沌展开的自适应稀疏方案Fig.2 Adaptive sparse scheme for gPC expansion

在稀疏gPC基选择方面，相比式(7)的传统标准截断策略，低阶交互截断方案认为只有变量之间的低阶交互才是重要的，从而通过舍弃标准gPC展开基集合中的某些高阶高秩项获得稀疏gPC基集合。这里采用如下低阶交互截断，亦称q-范数或双曲截断[22]

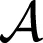
(13)

式中，‖·‖q为q-范数。当q= 1时退化为标准截断；当q<1时部分高阶高秩交叉项则会被剔除，且q取值越小剔除的项数越多。除了低阶交互截断，基于最小角回归可进一步获得更稀疏的gPC基集合。本质上，最小角回归是通过将候选集(candidate set)中与当前残差最相关的回归量逐步加入到有效集(active set)中来实现最优稀疏gPC基集合选取的。有关低阶交互截断、最小角回归及其在稀疏gPC基集合选择中的应用详见文献[22,26]。

一旦获得了当前阶数p下的最优稀疏gPC基集合*(p)，那么利用最小二乘法即可获得该稀疏集合对应的gPC展开系数{cα,α∈*(p)}。同时，为了评估该稀疏集合下gPC近似模型的精度，这里采用基于留一法的后验交叉验证误差估计

(14)

(15)

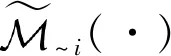
经过一系列循环后，依据最小的εLOO即可获得最佳的gPC展开阶数

(16)

3 工程算例

3.1 算例描述

本节以某型跨座式单轨车辆为研究对象，建立该型单轨车辆在R300曲线段以不同速度等级运行时的随机平稳性模型，在有限试验设计样本限制下，分别采用拉丁超立方体抽样方法和前述自适应稀疏广义多项式混沌方法，详细探讨车辆载重、悬挂元件刚度和阻尼、轨道参数和轮轨界面参数的随机性影响下的单轨车辆随机平稳性统计分布规律，同时对比两种方法的优劣。

为此，在已有研究基础上，并结合专家经验取式(5)中的11个输入参数作为随机向量，设各随机参数服从正态分布或截尾正态分布，相应的分布参数列于表2。其中，考虑到单轨车辆在空载和超载下的重量限制，设定车辆载重m的截尾区间为[14 220，25 800]；按GB 50458—2008设定轨道超高率h最大截断点为12%；同时限制轮轨动摩擦因数μ1和静摩擦因数μ2的分布区间分别为[0.7，0.9]和[0.9，1.3]；而其余各元件的刚度和阻尼参数由于没有明确的上/下限值规定，这里将它们取为非截尾的正态分布。此外，考虑空气弹簧刚度和车辆载重之间存在的正相关性，并用Spearman相关系数描述，其中车辆载重m与空簧垂向刚度kz和空簧横向刚度kxy的相关系数均设为0.7，空簧垂向刚度kz和横向刚度kxy的相关系数设为0.8。

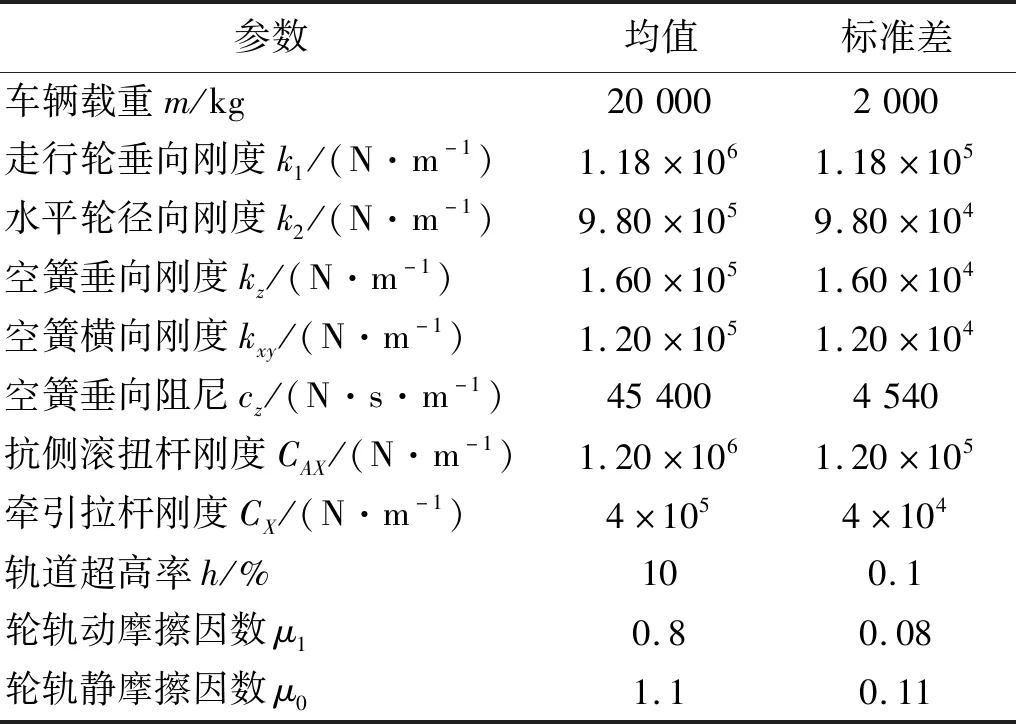
表2 随机参数取值Tab.2 The values of stochastic parameters

算例中以确定性的轨道不平顺样本模拟轨道激励，并取V1=45 km/h，V2=60 km/h和V3=75 km/h三种单轨车辆运行速度工况，同时考虑到UM数值仿真模型的高昂计算量，这里限制每一速度等级的试验设计样本数目为200组，并采用拉丁超立方体抽样技术获得试验设计样本。为便于比较，取三种速度等级下的200组试验设计样本保持一致，并计算该200组样本在三种速度下的单轨车辆横向平稳性和垂向平稳性指标，以获取输入输出试验设计数据。参照规范GB/T 5599—1985，跨座式单轨车辆的横向和垂向平稳性指标分别由车体1位端心盘一侧1 000 mm地板面上一点的横向和垂向振动加速度数据按式(2)计算得到。

3.2 基于LHS样本的随机分析

图3和图4是依据200组LHS样本数据直接绘制的三种速度等级下单轨车辆横向和垂向平稳性指标的直方图及其正态分布拟合，并估算了相应的前四阶矩(均值、标准差、偏斜度和峰度)和样本极差，列于表3。

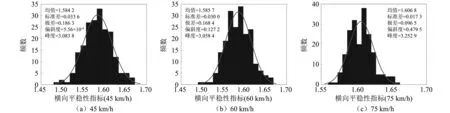
图3 基于LHS样本的横向平稳性指标分布Fig.3 Lateral stationarity index distribution based on LHS samples

从均值统计量角度，可以看到：①同一速度等级下，该型跨座式单轨车辆的垂向平稳性指标均值要大于横向平稳性指标均值；②在三种速度等级下，横向平稳性指标随运行速度增加而增加(1.584 2,1.585 7,1.606 8)，但增幅却不大，尤其是45 km/h和60 km/h速度等级之间相应增幅不超过1‰，而60 km/h和75 km/h速度等级之间的增幅低于1.5%；③在三种速度等级下，垂向平稳性指标从45 km/h的1.821 4先略微下降到60 km/h的1.817 1，之后又相对显著地增加到了75 km/h的1.934 0。这些均值结果规律与传统的确定性平稳性分析规律较为一致[24]，间接验证了计算模型的正确性。

从统计离散性来看，三种速度等级下的横向和垂向平稳性指标，无论是标准差还是极差，随着速度的增加均呈现减小趋势，其中横向平稳性指标从60 km/h到75 km/h的离散性下降较为明显(如标准差从0.030 0降到0.017 3)，而垂向平稳性指标的离散性则是在45 km/h和60 km/h下降相对明显。表明随着车辆响应量的增加，随机参数随机性对平稳性指标的离散性影响整体在下降。

从样本数据的偏态分布来看，横向和垂向平稳性指标的偏斜度随着三个速度等级的增加而增大，其中45 km/h时两种平稳性指标的偏斜度均比较接近零，分别为5.56×10-4和0.058 4，表明该速度工况下的随机平稳性指标呈对称分布形式，而60 km/h和75 km/h速度下的偏斜度均明显大于零，尤其是75 km/h速度时的垂向平稳性指标偏斜度达到了0.750 5，使得分布呈现明显右偏态，即有更多的样本数据落在均值右侧且右侧尾部较长，如图4(c)所示。

从峰度统计量角度，三种速度等级下的横向和垂向平稳性指标，以60 km/h时的峰度值最小但均大于3，表明相比正态分布，各平稳性指标在分布峰值处更为陡峭。其中，横向平稳性指标在45 km/h和60 km/h时以及垂向平稳性指标在60 km/h时的峰度值均比较接近3，分别为3.083 8，3.054 8和3.036 0，因而可以近似认为它们具有和正态分布一致的峰态。不过，45 km/h时的垂向平稳性指标和和75 km/h时的横向和垂向平稳性指标的峰度值是明显大于3的，分别为3.200 4，3.252 9，3.975 7，表明这些情况下的分布峰值和尾部特征与正态分布差异较大。

不过，需要注意的是，虽然拉丁超立方抽样利用分层抽样原理可做到以较小样本数目获得较高的抽样精度，但在这里200组有限样本数据限制下，其对高阶统计矩(如偏斜度、峰度等)的估计精度仍然误差较大，因此本小节基于LHS样本的单轨车辆随机平稳性指标统计规律的结论不一定完全正确，尤其是针对高阶统计矩的规律(见表3)。这一问题在下一节讨论。

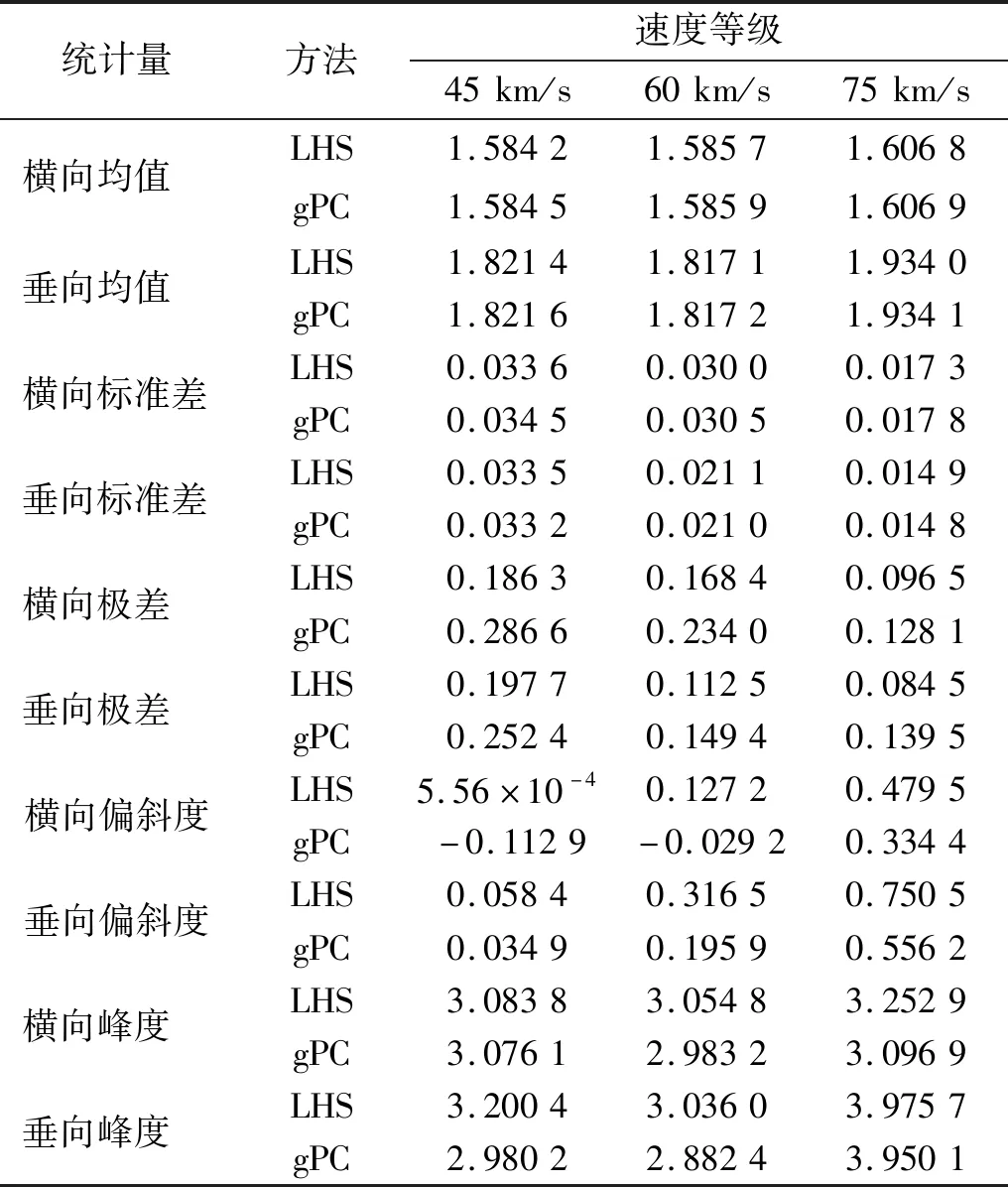
表3 三种速度下随机平稳性指标的统计矩Tab.3 Statistical moments of stochastic stationarity index for three different speeds

3.3 基于gPC近似模型的随机分析

将前述200组拉丁超立方试验设计数据作为训练样本，利用文中给出的自适应稀疏展开方案，设定低阶交互截断参数q=0.75，最高展开阶数范围p∈[2,10]，建立单轨车辆随机平稳性指标的最优gPC近似模型。

3.3.1 gPC近似模型及其验证

表4给出了三种速度等级下自适应稀疏gPC近似模型的构建情况。可以看到，不同速度下横向和垂向平稳性指标的gPC模型都具有较高的近似精度(误差量级10-4)。以60 km/h时垂向平稳性指标的gPC近似模型为例，在标准截断下由式(8)可以计算出11维5阶gPC展开项数为4 368项，远超过已知的200组试验设计数目，但采用式(13)低阶交互截断方案后，项数降低至496项，之后再利用LAR稀疏选择方案，项数更是降低到33项，此时利用OLS算法即可估算出gPC展开系数，构建出gPC近似模型，且留一法误差εLOO为5.61×10-4，模型精度很高。而该工况下的最佳阶数p*= 5正是在最高阶数展开范围p∈[2,10]内自适应运算的结果。

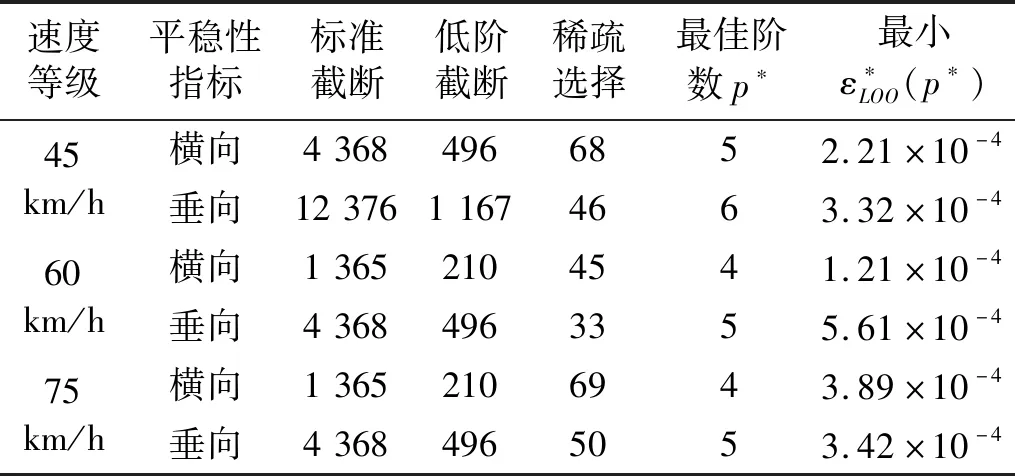
表4 自适应稀疏gPC近似模型的构建Tab.4 Construction of adaptive sparse gPC approximation model

为了进一步验证构建的gPC模型近似精度，这里基于拉丁超立方抽样方法再额外计算出100组试验设计点作为验证集，并采用泛化误差估算

(17)

(18)

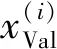
表5 基于验证集的gPC模型近似精度Tab.5 The accuracy of gPC models based on validation set

图5 75 km/h时平稳性指标的真实值和gPC近似值散点图Fig.5 Scatter plot of the statinarity index of real model and gPC model at 75 km/h

3.3.2 基于gPC模型的结果分析

在前述gPC近似模型基础上，开展20 000组大样本数据抽样。图6和图7是利用获得的20 000组样本数据绘制的三种速度等级下单轨车辆横向和垂向平稳性指标的直方图及其正态分布拟合，并估算了相应的前四阶矩(均值、标准差、偏斜度和峰度)和样本极差，列于表3。可以看到：相比前述基于200组有限数据的直接LHS结果，在基于gPC近似模型的20 000组大样本数据下绘制的统计直方图可以更精细地表达单轨车辆随机平稳性指标的分布规律。

对比三种速度等级下的各阶统计矩信息(见表3)，可以发现LHS和gPC两种方法下的统计数据变化规律是基本一致的。特别是，前两阶统计矩(即均值和标准差)数据，不仅变化规律一致，数据大小的差异也非常小，这也从侧面证明了建立的自适应稀疏gPC近似模型的正确性。不过，两种方法下的更高阶统计矩(如偏斜度和峰度)数据则差异比较大。以45 km/h时的LHS结果和gPC结果为例，垂向平稳性指标的偏斜度分别为0.058 4和0.034 9，峰度分别为3.200 4和2.980 2，差异明显。考虑到本算例中建立的自适应稀疏gPC模型在近似精度上有保证，因此将获得的gPC结果作为探讨单轨车辆平稳性指标统计规律的依据是合理的。

为此，基于gPC结果，同时考虑到前两阶矩差异性较小，这里仅对上一节基于LHS结果的偏斜度和峰度规律进行部分修正。在偏态方面，基于gPC的横向和垂向平稳性指标的偏斜度，同样是随着三个速度等级的增加而增大的。不过，相比LHS结果，所有偏斜度大小均有所下降，其中45 km/h和60 km/h时横向偏斜度减小到了负值，表现出左偏态，说明随着速度等级的增加，单轨车辆的横向平稳性指标分布偏态是由左偏态逐步过渡到右偏态的。从偏态程度上看，60 km/h时横向偏斜度和45 km/h时垂向偏斜度均非常接近零，分别为-0.029 2和0.034 9，表明这两种情况下的随机平稳性指标可认为呈对称式分布，而其余情况下的横向和垂向偏斜度绝对值均明显大于零，尤其是75 km/h时横向和垂向偏斜度分别达到了0.334 4和0.556 2，呈现出明显的右偏态，使得更多的样本数据落在了均值右侧且具有较长的右尾部，如图6(c)和图7(c)所示，这表明：单轨车辆运行速度越大，出现较大平稳性指标的概率也越高，使得列车舒适性体验下降。

在峰态方面，三种速度等级下，基于gPC的横向和垂向平稳性指标，虽然仍以60 km/h时的峰度值最小，但相比LHS结果，所有峰度值大小有所下降，其中60 km/h时的横向和垂向峰度值以及45 km/h时的垂向峰度值更是下降到了3以下，分别为2.983 2，2.882 4和2.980 2，说明这些随机平稳性指标的峰态比正态分布更为平缓。而45 km/h时的横向峰度值和75 km/h时的横向和垂向峰度值则仍然大于3，分别为3.076 1，3.096 9和3.950 1，具有比正态分布更陡峭的峰态，尤其是75 km/h的垂向平稳性指标，其分布特征与正态分布在峰值和尾部方面有较为显著的差异，如图7(c)所示。不过，除了75 km/h时的垂向峰度值(即3.950 1)，其余各速度等级下的横向和垂向峰度值均较为接近3，差异值很小，可以近似认为与正态分布有一致的峰态。

最后，以GB/T 5599—1985中客车运行平稳性等级作为单轨车辆平稳性评定标准，可知当横向和垂向平稳性指标Y<2.5时，平稳性等级为1级，评定为优。从图6和图7中可以看到，即使考虑参数的随机性，本算例中三种速度等级下的该型单轨车辆的横向垂向平稳性指标超出2.5的概率也是微乎其微。以算例中最大的75 km/h的垂向平稳性指标为例，基于20 000组试验设计样本可得：统计均值为1.934 1，标准差为0.014 8，超出阈值2和2.5的样本个数分别为16和0，对应的样本估算失效概率分别为0.8‰和0‰。说明本算例所涉工况的单轨车辆平稳性等级为优。

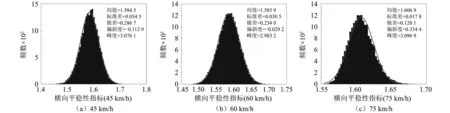
图6 基于gPC模型的横向平稳性指标分布Fig.6 Lateral stationarity index distribution based on gPC model

图7 基于gPC模型的垂向平稳性指标分布Fig.7 Vertical stationarity index distribution based on gPC model

3.4 随机平稳性灵敏度分析

利用前述构建的gPC近似模型，依据式(11)和式(12)可直接获得三种速度等级下横向和垂向平稳性指标对各随机变量的Sobol全局灵敏度，如图8、图9和表6所示。这里仅讨论横向和垂向随机平稳性指标的一阶和总的Sobol灵敏度。

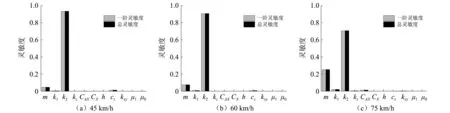
图8 基于gPC模型的横向平稳性指标灵敏度Fig.8 Sensitivity of lateral stationarity index based on gPC model

可以看到，对横向平稳性指标方差贡献最大的随机参数是水平轮(即导向轮和稳定轮)的径向刚度k2，其次是车辆载重m；对垂向平稳性指标方差贡献最大的随机参数是走行轮垂向刚度k1，其次是空簧垂向阻尼cz，再次是车辆载重m；而其余各随机参数对平稳性方差的贡献相对就非常小，也意味着它们在单轨车辆随机平稳性分析中通常是可以被忽略掉。

进一步，对比三种速度等级下的Sobol灵敏度，可以看出：随着运行速度的增大，车辆载重m对横向和垂向平稳性指标方差的贡献均呈增大趋势；走行轮垂向刚度k1对垂向平稳性指标方差的贡献则呈减小趋势；水平轮径向刚度k2对横向平稳性指标方差的贡献逐渐减小；空簧垂向阻尼cz对垂向平稳性指标方差的贡献在逐渐增大。

另外，对比三种速度等级下一阶Sobol灵敏度和总的Sobol灵敏度可知，两者的数据差异很小，这说明在本算例中单轨车辆平稳性指标的离散性受随机参数交互作用的影响是较小的。不过，随着运行速度的增加，这种随机参数交互作用的影响也在逐渐增大，如75 km/h时垂直平稳性指标对车辆载重m和走行轮垂向刚度k1的一阶和总的Sobol灵敏度数据差异就比较明显了，如表6和图9(c)所示。

表6 三种速度下垂向平稳性指标的Sobol灵敏度Tab.6 Sobol sensitivity of vertical stationary index under three different speeds

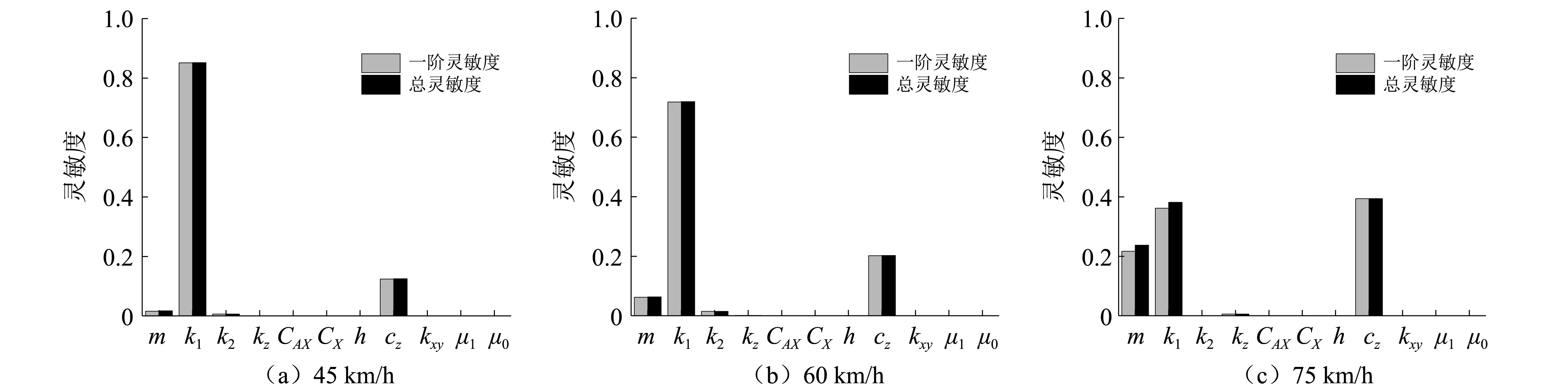
图9 基于gPC模型的垂向平稳性指标灵敏度Fig.9 Sensitivity of vertical stationarity index based on gPC model

4 结 论

(1)提出了以横向和垂向平稳性指标为关键响应量的单轨车辆运行平稳性随机分析和灵敏度计算方法；同时，借助参数化UM建模和仿真功能可以实现任意输入参数影响下单轨车辆复杂响应量的模型函数建立。

(2)给出的gPC自适应稀疏方案可基于现有有限的试验样本数据极大地降低随机平稳性分析模型的随机维度(即总展开项数)，并达到自适应范围内的最佳gPC模型近似精度。与直接采用拉丁超立方抽样方法相比，基于gPC近似模型的随机结果更为准确可靠，尤其是高阶统计矩。

(3)该型跨座式单轨车辆在三种速度等级下的平稳性指标整体呈现正态分布规律，其中同一速度等级下垂向平稳性指标均值要大于横向平稳性指标均值，并且随着速度的增加各平稳性指标的离散性(标准差和极差)在减小；而在高阶矩方面，速度增加则引起平稳性指标的偏斜度和峰度增大，尤其是在75 km/h时，表明运行速度越大单轨车辆出现较大平稳性指标的概率也越高，使得列车舒适性体验下降。不过，即使受到输入参数随机性的影响，本算例所涉工况的平稳性等级仍为优。

(4)车辆载重m、走行轮垂向刚度k1、水平轮径向刚度k2、空簧垂向阻尼cz是影响单轨车辆平稳性指标方差的主要随机参数。其中，在垂向平稳性方面，随着速度的增大，m和cz的贡献增大，k1的贡献减小；而在横向平稳性方面，m的贡献增大，k2的贡献减小。