驻波场中圆柱形换热管外声流特性的数值研究

杨延锋，姜根山，姜 羽

(1.华北电力大学 能源动力与机械工程学院，北京 102206；2.华北电力大学 数理学院，北京 102206)

声波引起的振荡流遇到固体或固体在静止流体中做自激振荡时，由于黏性和惯性的非线性相互作用，将在固体边界层内外形成稳态涡流的现象，这种现象在流体力学中被称为“steady streaming”，即定常流动；而在声学领域则被称之为“acoustic streaming”，即声流[1]。

已有研究表明，声流在促进固-液(气)界面的某些速率过程，包括对流换热、燃烧和去除松散的表面层方面特别有效[2]。国外Davidson等[3-5]对圆柱管做小振幅周期性振动诱导的声流强化传热进行了理论分析。Tajik等[6]试验测量了水平受热面上充水封闭圆柱壳在声流作用下的强化传热。结果表明，在超声振动产生的声流作用下，热源与振动板附近的水之间的传热强化可达390%。Aktas等[7]研究了典型和驻波声场引起的不规则流运动对封闭空间内对流换热的影响。研究表明，在存在不规则流的情况下，传热增强效果更为明显。姜波等[8-10]采用数值模拟与试验相结合的方法，研究了低频振动管外的流动与传热特性。研究表明，振动有利于强化传热，且其强化传热的效果随着振动频率与振幅升高而增强。刘建华等[11]通过求解二维非定常雷诺时均Navier-Stokes方程，对二维管内可压缩流动模型进行数值模拟，分析壁面振动对流场及传热的影响。研究发现，壁面局部振动对下游流场造成一定扰动，但在传热方振动的壁面只在一定的相位区间才能增强换热。吕平等[12]利用试验的方法研究了水平圆管在高频低振幅的横向振动条件下，管内流体的传热特性。试验结果表明：随着振动频率的增加管内对流换热系数先增大，达到峰值(共振频率下)后迅速减小，最终趋于稳定。吴艳阳等[13]采用Fluent动网格技术研究了振动圆管内流体流动与换热特性，并采用场协同的方法进行分析，发现振幅为1～5 mm，频率为2～10 Hz，振动能强化传热，且传热效果随振动频率和振幅的增加而增强，传热系数最多提高71%，并指出当相位为90 ℃时场协同性最好，传热效果最好。Shi等[14]研究了自由柔性振动片在流体通道内的换热情况，使用CFD(computational fluid dynamics)和CSD(computational structural dynamics)求解器相耦合的方法，利用ALE(arbitrary Lagrangian eulerian )处理变形网格，得出流道传热强化90.1%。林同骥等[15]对单圆柱做小振幅简谐振荡诱导定常二次旋涡流动进行了理论和试验研究。姜根山等[16]基于Lee研究中圆柱边界层外的声流理论对电站锅炉换热管外的声流进行了简单数值计算。

综合以上的研究发现，国内外学者虽然对圆管做周期性振动引起的强化传热进行了大量的研究，但很少有对不同振幅和振动频率下圆柱管外声流流场结构的具体研究。因此，笔者以某电厂630 MW锅炉中屏式过热器末级换热管为研究对象，利用有限元软件COMSOL实现了对平面驻波声场中单圆柱形换热管和双圆柱形换热管外包含边界层内外二阶流场信息Navier-Stokes方程的全域求解，探究了换热管外声流结构特征。该问题的研究将有助于对振动热管或脉动流场传热机理的理解。

1 控制方程

1.1 声流控制方程

黏性流体运动由Navier-Stokes动量方程和连续性方程控制

(1)

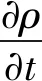
(2)

式中：u为流速矢量；P为流体的压强；μB为体积黏滞系数；μ为切变黏滞系数。圆柱边界层内外的声流主要受到切变黏滞系数μ的影响。

声波扰动下，考虑二阶流场信息的流场变量可表示为

p=p0+εp1+ε2p2

(3a)

ρ=ρ0+ερ1+ε2ρ2

(3b)

u=εu1+ε2u2

(3c)

式中：ε为一阶变量小参数，ε=U0/c≪1；变量的下标0，1，2分别为静态量、一阶量和二阶量。一阶速度、压力和密度是时间的谐波函数(e-iωt)，由声波方程控制。而二阶量是非线性现象的体现，即声流。

将式(3)代入式(1)和式(2)中，可得到一阶流场满足的动量方程和连续性方程

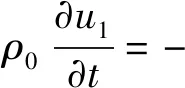
(4)

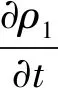
(5)

(6)

式中，c0为流体中的声速。如流体为不可压缩，则式(4)可变为

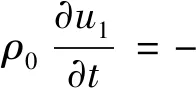
(7)

同理，将式(3)代入Navier-Stokes方程并保留二阶量，则可得到声流的控制方程

(8)

(9)

因为声流是与时间无关的稳态流，因此分别对式(8)、式(9)取时间平均可得声流的控制方程

ρ0·〈u2〉=-·〈ρ1u1〉

(10)

-〈(·〈u2〉)=
)u1〉

(11)

式中，〈〉为对物理量在整个振荡周期内取时间平均。由式(10)、式(11)分析知，一阶场量是驱动二阶场量的源项。式(10)右边的一阶场量为驱动二阶场量的质量源；式(11)右边的一阶场量为驱动二阶场量的体积力。

1.2 热黏性声学理论基础

当声波引起的振荡流作用在换热管上时，在其边界层内的黏性损失和热传导是声流形成的关键因素。因此，有必要在声流控制方程中明确地包含热传导效应和黏滞损失。

热声场的扰动控制方程为[17]

dρ=γkρdp-αρdT

(12)

(13)

式中：d为对变量取全微分形式；Cp为常压下的比热容；γ为比热比；k为等熵压缩系数；α为等压热膨胀系数。同样，声波扰动下的温度场可描述为

T=T0+T1+T2

(14)

将式(14)和式(3a)代入式(12)、式(13)可得到关于一阶温度场T1的热力学传热方程

(15)

(16)

式中，λ为流体的导热系数。由于流体一阶场的非线性相互作用发生在换热管表面附近的声学边界上。因此，必须精确求解热黏滞边界层附近的声学问题。声波作用下，换热管附近的黏性边界层和热边界层可由式(17)评估[18-19]

(17)

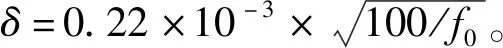
2 数值模型

有限元软件COMSOL中的热黏性声学模块可精确模拟声波在换热管声-热边界层与黏性边界层中的损耗。而为模拟出换热管外声学边界层，需在换热管外壁上施加一个等温无滑移条件uT=0。等温条件是一种非常有效的近似处理方式，因为固体内的热传导通常比流体高出几个数量级。这两个条件可生成由黏性边界层和热边界层构成的声学边界层。

2.1 几何模型

本文以某电厂630 MW锅炉中屏式过热器末级换热管为研究对象。换热管直径D=38.1 mm，其外围计算域为直径的10倍，即L=381 mm；换热管纵向节距为SL=76.2 mm。在频域热黏性声学模块下，计算域两侧的边界条件选取垂直于边界的速度边界，该边界条件可使换热管始终处于速度波腹(或声压波节)位置处。换热管外壁选取硬壁无滑移等温边界。计算域上下侧选取对称边界。图1给出了单根圆柱换热管外的边界条件及计算域网格划分。

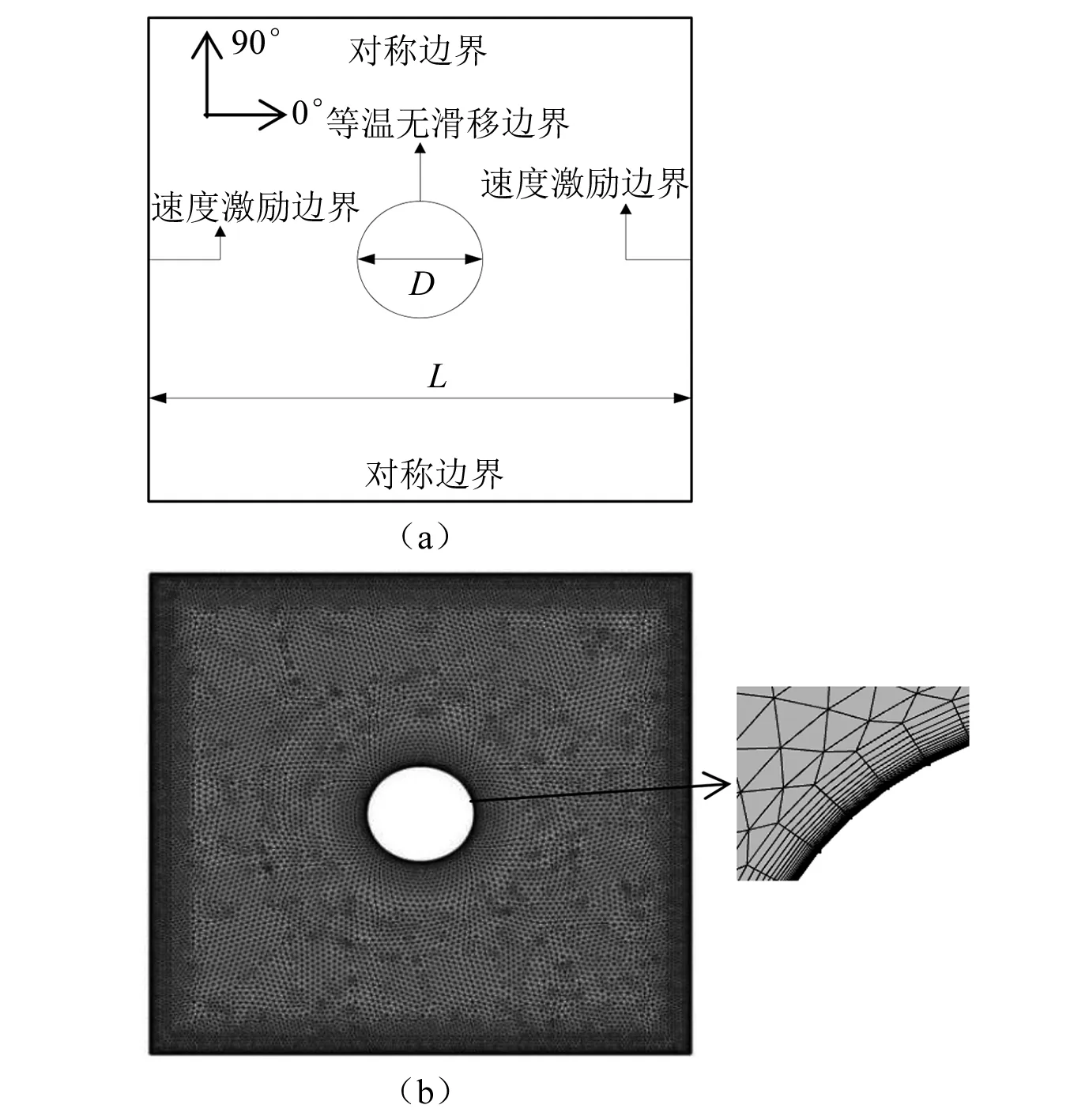
图1 边界条件及网格划分Fig.1 Boundary conditions and mesh generation

为捕捉到黏性边界层δ和热边界层δth，最小网格尺度选取δ/10，不同边界层厚度比为1.2，边界层数选取20以完全覆盖声学边界层。换热管边界层内生成自由四边形网格，而边界层外生成三角形网格。计算域内网格划分如图1所示。选取1 200 ℃的空气作为计算介质，其主要参数如表1所示。

表1 计算介质主要参数Tab.1 Main parameters of calculation medium

2.2 计算方法

由式(10)、式(11)可知，一阶无旋场是驱动二阶有旋场的源项。基于此，可利用有限元软件COMSOL对声流控制方程进行分步求解：

步骤1利用频域热黏性声学模块对在速度边界或压力边界条件激励下形成的一阶无旋场(p1,u1,T1,ρ1)进行求解；

步骤2采用CFD单相层流模块求解式(10)、式(11)控制的时均二阶有旋场。将步骤1得到的时均一阶场作为源项来求解一阶声场引起的非线性二阶声流场。这在有限元软件COMSOL中可通过添加弱贡献的方式，分别将式(10)、式(11)右边的时均一阶场中的质量源项和体积力项加入到方程右边求解。

2.3 网格独立性检验及数值模型验证

数值模拟的可靠性验证是判断数值模拟可信度的一个重要方面。此外，在保证计算精度的条件下需要尽量降低计算资源，即需对网格独立性进行检验。由于我们关注的是二阶声流场，据此选取最大二阶声流速度u2max作为网格独立性评估标准。图2给出了速度边界振幅和频率分别为0.01 m/s，1 kHz时，最大二阶声流速度u2max随网格数的变化图。

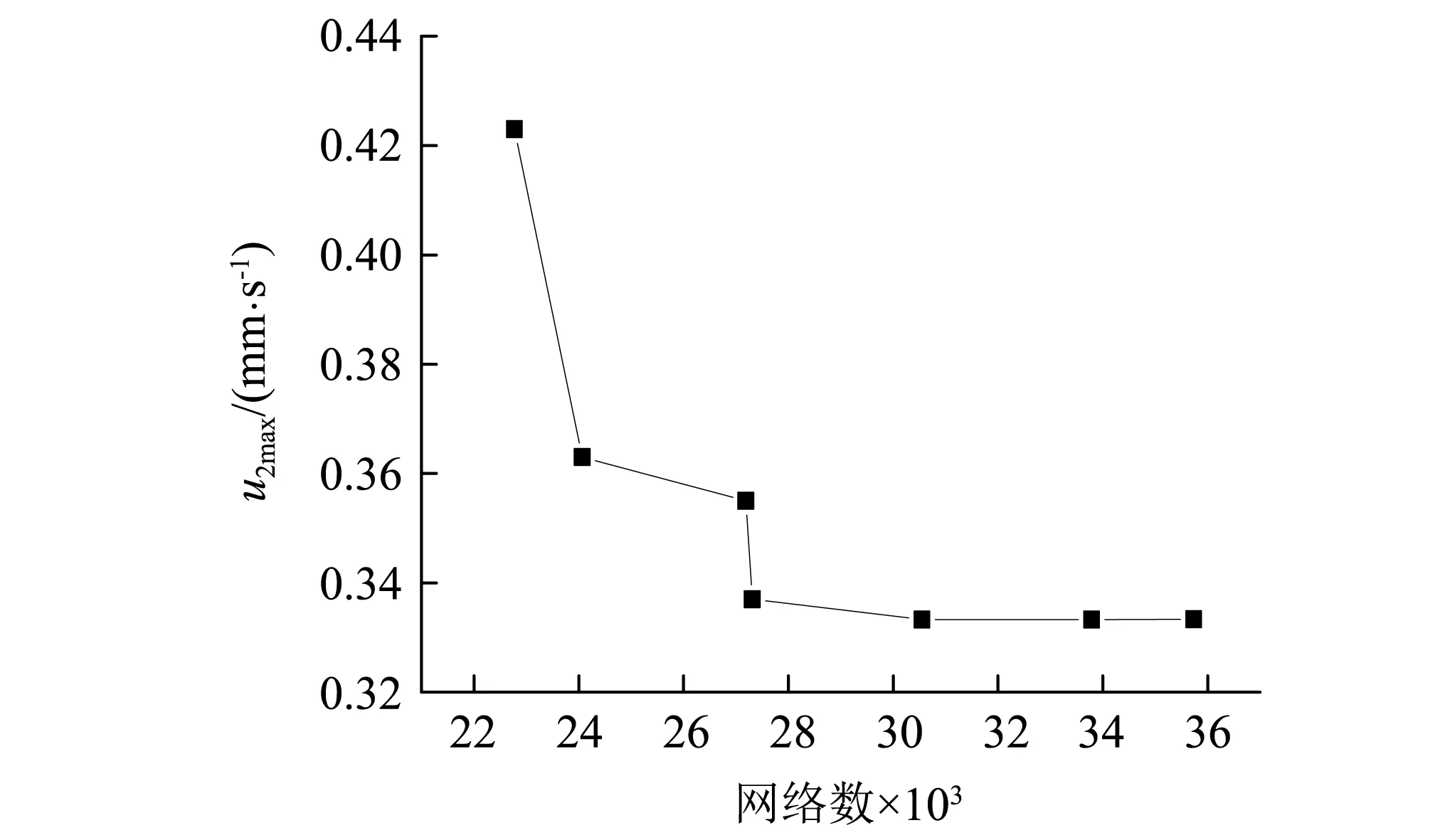
图2 网格独立性检验Fig.2 Grid independence test

从图2可以看出，网格数为30 550，33 790和35 734个时，对u2max几乎没有影响，因此本研究使用了30 550个网格数。而一般来讲，网格越精细数值解越准确。在总网格数(30 550)和边界层数(20)不变的条件下，分别取最小网格厚度为：δ/5，δ/10，δ/15，以此分析最小网格引起的计算误差。数值计算表明，最小网格引起的误差小于1%。

为验证数值模型的可靠性。在满足声波波长远大于换热管半径的条件下(λ≫R)，将换热管外二阶声流速度的数值解与Lee关于圆柱边界层外声流速度的解析解进行对比。数值计算和Lee的理论计算都表明，在满足λ≫R的条件下，圆柱管外的声流结构呈轴对称分布，因此分别取45°和0°方向二阶声流速度做验证对比。计算参数为：U0=0.01 m/s，f0=1 kHz。Lee关于圆管边界层外二阶声流的解析解为

(18a)

(18b)

式中：u2θ，v2r分别为轴向和径向二阶流速分量；A为外源激励振幅。将解析解和数值解分别在45°和0°方向的二阶声流速度大小进行归一化处理后进行对比，如图3所示。

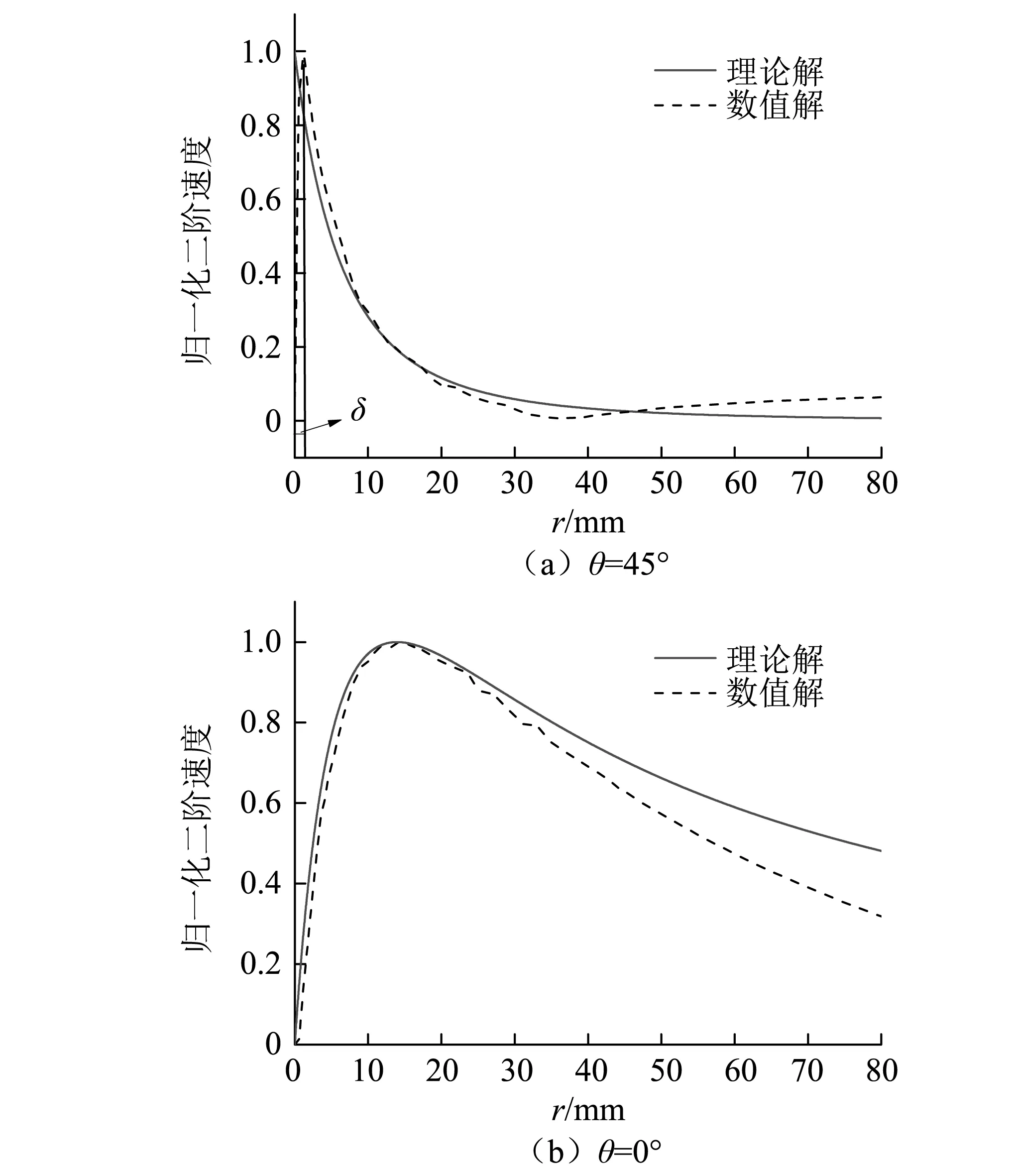
图3 数值解与Lee的解析解对比Fig.3 Comparison between numerical solution and Lee analytical solution

由图3可知，数值解与Lee的解析解在45°和0°方向的径向二阶速度大致是吻合的。由于数值解捕捉到了换热管外薄黏性边界层内(δ=6.957×10-5m)的物理场信息，因此在45°方位上，数值解和解析解存在一定差异；在0°方向，随着r的增大，数值解和解析解偏离变大，这与换热管外空间声场分布有关，即声波波长λ越大，换热管半径R越小，管外空间声场分布便越均匀，这时数值解与Lee的解析解越吻合。但数值解更能反应换热管外实际的物理规律，因为数值模型求解的是包含边界层内和边界层外全域的N-S方程，而Lee给出的只是边界层外理想的解析解。

3 结果及分析

3.1 计算域内平面驻波声场分布特性

计算域左右侧采用有限元软件COMSOL中频域热黏性声学模块下的速度边界作为激励源：u0x=n·u1=U0e-iωt=0.01e-iωt，方向平行于x轴。使计算域内形成特定的平面驻波声场。激励频率取：f0=1 kHz。其一阶声场分布如图4所示。

经计算表明，采用速度边界作为激励源，能使换热管总处于声压波节或速度波腹位置。从图4一阶声压云图中可以看出，换热管的存在对周围空间的声压造成了一定影响，这是因为换热管特征尺度与波长的数量级相当，换热管本身的散射声场与入射声场叠加的结果。因此，为保持入射声场的单一性，需满足声波波长远大于换热管半径，即λ≫R。

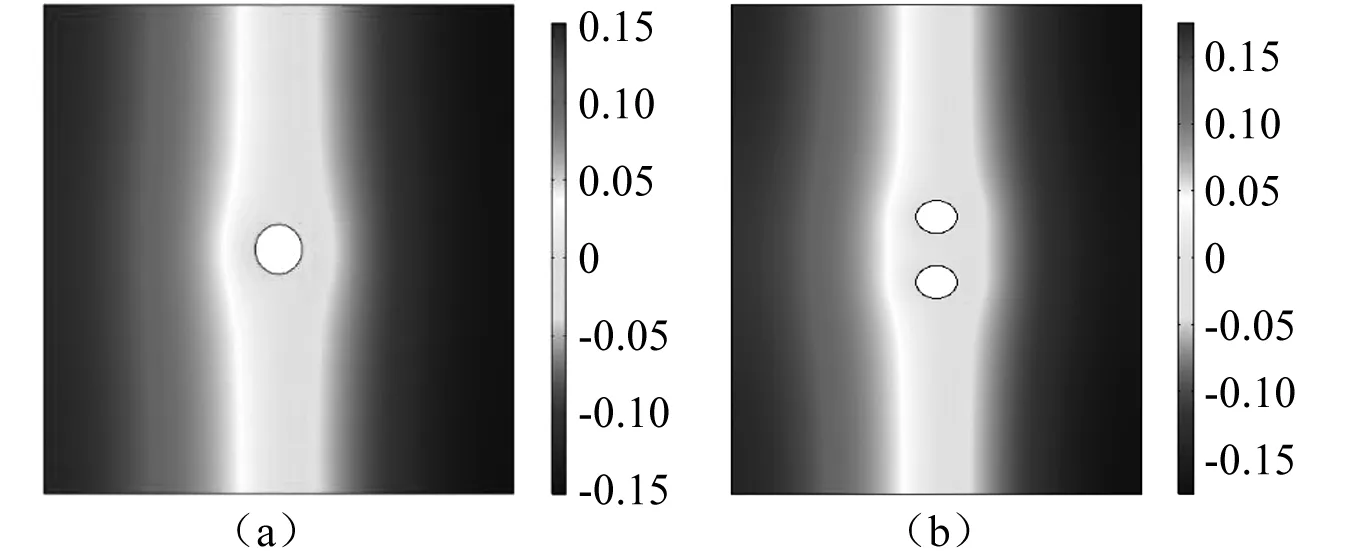
图4 速度边界作为激励源产生的平面驻波声场Fig.4 Plane standing wave sound field generated by velocity boundary as excitation source

3.2 驻波场中换热管外声流的分布特性

本文主要考察了驻波声场中圆柱形换热管外的声流特性。基于3.1节的探究，模拟过程中波长与换热管半径之间始终满足：λ≫R。在这种限制下，换热管表面不会受到明显的声强空间变化的影响。这也是保证流体不可压缩性的必要条件。

一般来说，固体边界层内外的流动取决于固体特征尺度D、角频率ω、振荡振幅ζ0和运动黏度ν。因此，为描述换热管外声流特征得一般性规律，现定义以下无量纲数

(19)

式中：U0为速度振幅；ω为角频率；ζ0为位移振幅,ζ0=U0/ω。ε为声波引起的振荡流位移振幅相对于换热管直径的大小。当ε≪1时，表明换热管外的流场做小振幅波动；当ε≫1时，换热管外的流场将做大振幅波动，具有强烈的非线性作用。雷诺数Re为惯性力和黏性力之比。斯特劳哈尔数Sr则表征了非定常运动的强弱。为方便与前人的试验结果对比，数值计算中始终满足ε≪1。

3.2.1 斯特劳哈尔数Sr对单换热管外声流分布的影响

在满足kR≪1的条件下，对于给定Re=1.71，通过改变速度边界激励频率的方法，分别取Sr=239.39(f0=20 Hz)，598.47(f0=50 Hz)，1 196.9(f0=100 Hz)，11 969(f0=1 000 Hz)，35 908(f0=3 000 Hz)进行对比分析。为清晰显示换热管边界层内外的声流结构，显示区域仅取计算域的一部分。

图5 Sr对单换热管外声流结构的影响Fig.5 The influence of Sr on the structure of acoustic streaming outside the single heat exchange tube

对于给定的换热管尺寸，在满足λ≫R的条件下，声波引起的流体介质振幅始终满足ζ0=U0/ω=0.01/(2πf0)≪R。这表明，换热管外的声流运动对加快换热管的传热传质速率作用不大。而当声波引起的介质振荡振幅满足ζ0>R时，会出现边界层分离、快速流动等非线性现象，这将极大地强化换热管的传热传质效果。因此，为强化声流对换热管的传热效果，选择低频高强度声波将是最佳选择。

3.2.2 雷诺数Re对单换热管外声流分布的影响

对于给定Sr=239.39，通过改变速度边界激励频率和速度振幅的方法，分别取Re=4.28(f0=50 Hz,U0=0.025 m/s)，8.57(f0=100 Hz,U0=0.05 m/s)，85.66(f0=1 000 Hz,U0=0.5 m/s)，256.98(f0=3 000 Hz,U0=1.5 m/s)进行对比分析。

由图6分析知，Re较小时，换热管外的黏性作用和惯性作用相当，边界层内流仍能稳定存在，如图6(a)、图6(b)所示，这时在换热管外出现4个边界层内的涡流和4个边界层外涡流。对于特定的Sr，随Re增大，边界层内的涡流尺度减小,如图6(a)、图6(b)所示。且随着Re的继续增大，换热管外惯性力将远大于边界层内黏性力，这时换热管表面的边界层将发生分离，即振荡流破环了换热管表面的附面层，使黏性边界层内的声流无法稳定维持，这时在换热管外仅出现4个边界层外的涡流。而边界层的分离，将在换热管外形成范围更广的声流，这对强化换热管传热传质具有重要作用。

图6 Re对单换热管外声流结构的影响Fig.6 The influence of Re on the structure of acoustic flow outside the single heat exchange tube

综上，3.2.1节分析了单换热管处于声压波节位置时的声流结构。可想而知，换热管处于不同位置时其外部声流结构必然不同。但无量纲数(Re和Sr)对换热管外声流的影响规律具有一般性。

3.2.3Sr及Re对换热管外涡流强度及结构尺度的影响

由图7(a)、图7(c)可知，随Sr(Re=1.71)和Re(Sr=239.39)增大，黏性边界层厚度δ和d呈指数下降趋势，这表明随着Sr和Re增大，都使边界层内流尺度减小，使边界层外流尺度增大；同时，随着Sr和Re进一步增大，黏性边界层厚度δ和d对激励频率不再敏感，δ和d趋于平稳，这时边界层内流消失，边界层外流尺度达到最大。这由图5和图6的声流结构图清晰可见。

由图7(b)可知，u2max随Sr的增大呈指数形式下降，但随着Sr进一步增大，u2max对激励频率的影响不再敏感，这表明低频对声流强度影响较大，且低频声在换热管外诱导的声流越强、结构尺度越大，这有助于换热管与环境介质的强化传热。由图7(d)可知，u2max随Re的增大近乎呈直线增大，因为随着Re的增大，流体介质的非线性效应逐渐增大，即大雷诺数容易破坏边界层，并发生边界层分离，这时换热管外的介质扰动强烈，且换热管外的声流结构容易出现“撕裂”等现象[21]。

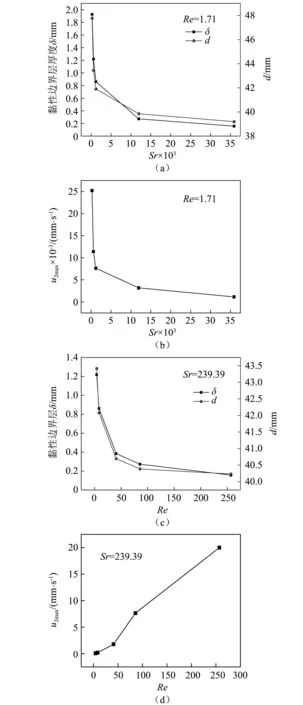
图7 Sr和Re对涡流强度及涡流尺度的影响Fig.7 Effect of Sr and Re on eddy current strength and scale

3.3 双换热管处于声压波节位置时其外部声流分布特性

屏式过热器为管阵列结构的换热部件，因此有必要对双换热管间的声流结构特性进行研究。同3.2.1节，对于给定Re=1.71，通过改变速度边界激励频率的方法，分别取Sr=1 196.9(f0=100 Hz)，11 969(f0=1 000 Hz)进行对比分析。图8给出了当双换热管位于声压波节位置时换热管间的声流结构。

由图8(a)观察知，对于给定Re，当Sr较小时，双换热管将出现包括8个边界层内的涡流和换热管间4个尺度较小的涡流以及4个管外尺度较大的涡流结构，共16个涡结构。而随着Sr增大，使δ≪R，边界层内的涡流结构将不能清晰呈现，这时双换热管外仅出现4个尺度较小的涡流和4个尺度较大的涡流，共8个涡结构，如图8(b)所示。由以上的分析知，与单换热管外的声流结构不同，由于换热管间振荡流存在相互作用而使双换热管间的声流结构更加复杂。

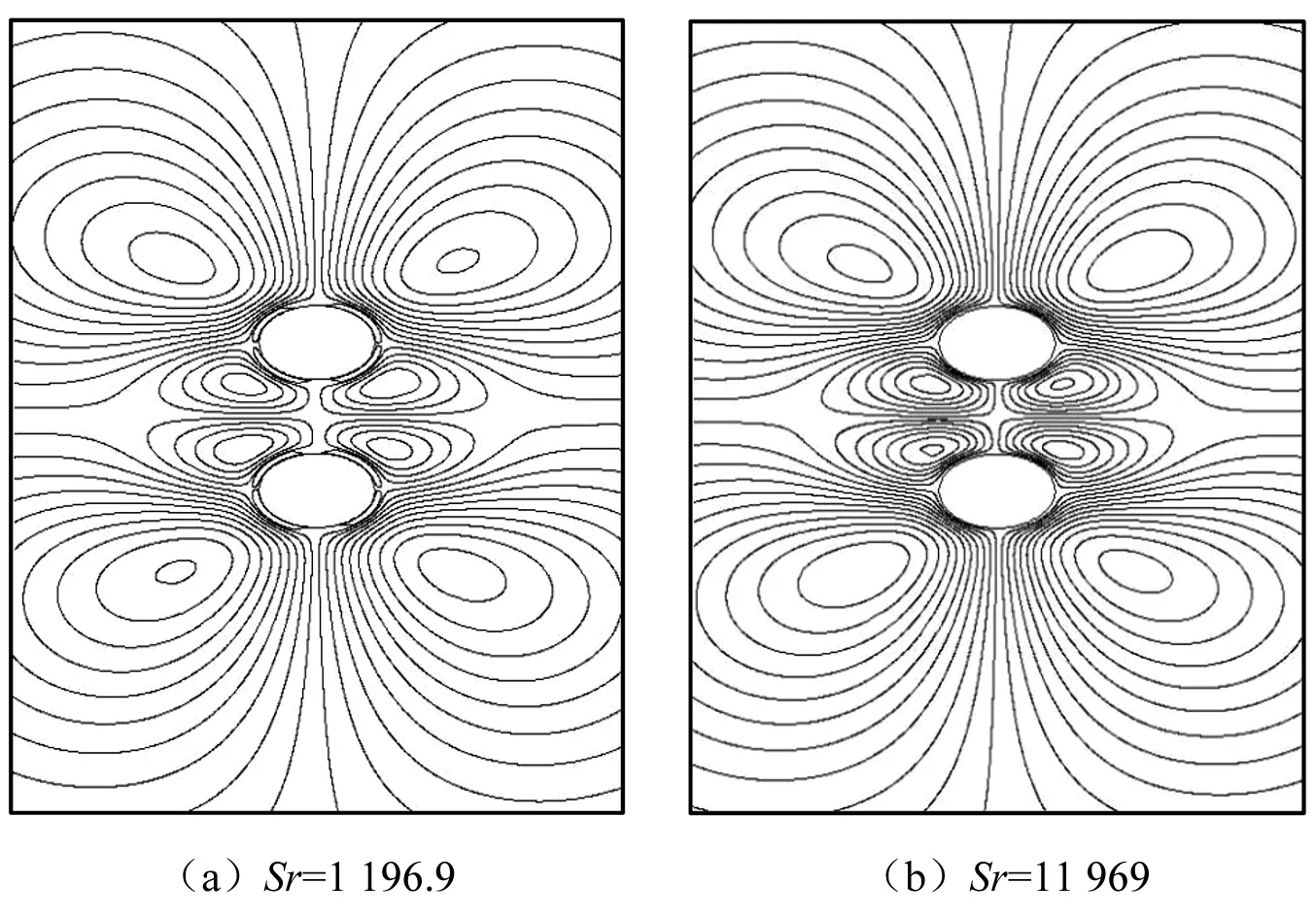
图8 双换热管间的声流结构Fig.8 Acoustic streaming structure between two heat exchange tubes

换热管间涡流结构的存在对清除表面积灰，强化传热传质过程具有重要作用。电站锅炉内换热管呈管阵列排布，介于换热管排列的周期性对称结构，对多排管阵列换热管外声流结构的研究就具有重要意义。该部分研究将在后面的文章中进行讨论。

4 结 论

基于前面的分析可知，对于声波引起的小振幅(ε≪1)振荡流与换热管相互作用而形成的声流与雷诺数Re和斯特劳哈尔数Sr具有重要关系。其结论如下：

(1) 对于满足λ≫R的单换热管处于声压波节位置时，其外部声流结构关于换热管呈空间均匀分布。且沿着振荡方向的流场是远离换热管，而在垂直方向流场是流向换热管的。

(2)Re和Sr较小时，换热管黏性边界层内的涡流是可视化的。而随Re和Sr的增大，换热管边界层内的涡流区域变小，直至消失；同时，边界层外的涡流区域逐渐增大。且薄层区域厚度越小，内部黏性切应力越大。

(3)Re和Sr较小时，单换热管外共出现8个涡流结构；而由于双换热管间振荡流的相互作用，双换热管外出现16个涡流结构。而随Re和Sr增大，单换热管外的涡流结构减少为4个；双换热管外减少到8个。

(4) 低频小振幅或大振幅声波在换热管外具有强烈的介质扰动，有利于换热管的强化传热。