面向MCNP程序的三维模型前处理技术研究

赵瑛峰， 刘检华， 马江涛， 武林林， 成勋

(1.北京理工大学 机械与车辆学院 数字化制造研究所，北京 100081；2.电子科技大学 信息与软件工程学院，四川，成都 610054)

蒙特卡洛方法作为核领域粒子输运问题模拟计算的重要方法，在核能开发、辐照计算、辐射防护、医学等领域发挥着越来越重要的作用.目前获得广泛应用的蒙特卡洛程序包括MCNP、FLUKA、GEANT4等，其中MCNP 是美国Los Alamos国家实验室研制的计算中子、电子、光子及其耦合问题的通用蒙特卡洛粒子输运计算程序，广泛应用于核领域的设计计算和评估分析[1].

目前，核领域粒子输运模拟计算存在建模困难的问题.一方面，MCNP的建模方式极为抽象、容易出错以及用户友好度差，对建模人员的专业性要求高，三维建模困难且效率低下.另一方面，CAD软件具有成熟高效的三维建模手段，但模型不能直接应用于MCNP系统.为了解决这一问题，国内外学者对面向MCNP计算的CAD模型前处理技术，即CAD模型向MCNP半空间CSG模型的转换进行了大量研究.如对BRep到半空间CSG描述的理论研究，提出了“规范相交项”和“可描述性定理”两个概念，从理论上证实了实体表面曲面阶数不超过二的任意三维实体的BRep到CSG转换的可行性，同时给出了一种分割半空间的生成方法[2].针对分割半空间方法冗余太多的问题，提出了一种求解最小可描述半空间集合的方法，这种方法计算复杂度高，是一个NP完全问题.为降低复杂度，进一步提出了基于特征点的计算近似最小可描述性半空间集的算法、基于主蕴含的CSG表达式化简方法.Buchele等[3]在前述研究的基础上提出了BHC算法，将BRep到BSP算法和BSP到CSG算法进行合并，并采用优势半空间概念，避免了每步操作后的中间实体的完整BRep数据结构的计算.

吴宜灿等[4]开发了建模软件系统MCAM，罗月童等在前人研究的基础上提出了基于分解的转换算法[5]，其包括CP-DS算法、HBDSS算法和HS-DS算法.该算法首先将实体分解为一组转换元，然后分别转换每个转换元，最后将转换元进行组合，生成实体的半空间表示.其中CP-DS算法通过“分解面”生成“转换元”、HBDSS算法用于分解面的选择、HS-DS算法则对生成的半空间表示进行化简并将该算法集成到MCAM软件中.周敬之等[6]提出了一种基于特征识别的CAD模型空腔生成算法，并将之集成到MCAM4.8版本，其提高了中空管道类模型的空腔构造速度.马露杰等[7]提出了一种基于面壳封闭分解BRep模型的方法，通过面壳上存在的面进行封闭，可分离出加体和减体，但未考虑生成CSG树.罗月童在马露杰研究基础上实现了基于面壳封闭的BRep到CSG转换算法[8].实验结果证明该算法模型普适性差，对于有些模型不仅优化效果差，而且额外增加计算量.另外，张建生等[9]研究了UG模型到MCNP几何模型的转换方法，实现了部分简单UG模型到MCNP几何模型的转换.

以上研究中，MCAM是基于Spatial公司的ACIS几何内核和数据交换组件实现.然而商业CAD模型需要通过数据交换组件转换为SAT才能被识别，不可避免地会存在模型裂缝、交叉、不一致等缺陷，需要进行大量的模型修复和处理工作才能使用.另外，张建生等的研究对UG模型的建模方法有限定，难以实现复杂和不遵循建模限定的模型的转换.

针对转换过程中存在大量模型修复和处理工作的问题，文中研究了应用于MCNP程序的三维CAD模型前处理技术.该技术通过商业CAD模型的预处理、空腔区域生成以及模型转换等算法将商业CAD模型转换为MCNP半空间CSG模型.基于上述研究，开发了MCNP三维前处理软件系统，并进行了实例验证.实例验证结果表明文中的方法能够高效地实现复杂商业UGNX CAD模型向MCNP半空间CSG模型的转换.

1 应用于MCNP程序的三维模型前处理技术路线

基于空间分解的三维CAD模型向MCNP半空间CSG模型的转换方法的总体技术路线如图1所示，具体可以分为4个步骤：

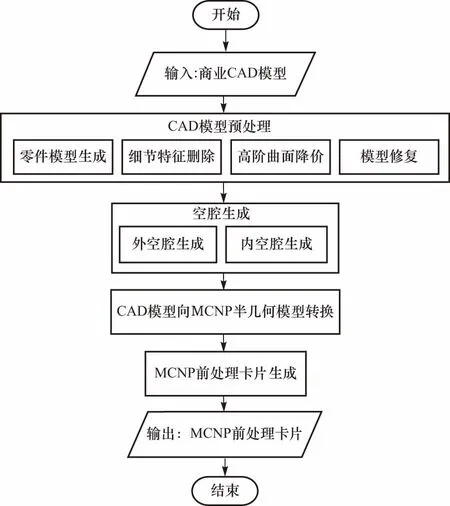
图1 总体技术路线

① CAD模型预处理.主要进行装配模型到零件模型生成、细节特征的删除、高阶曲面降阶以及外部输入模型的修复等.处理后的模型仍为CAD模型，但此时的模型适合于MCNP粒子输运计算.

② 空腔区域生成.空腔区域包括内部空腔和外部空腔，其中外部空腔为MCNP计算区域外的几何空间，内部空腔是MCNP计算区域内的材料为真空或者空气的几何区域，即计算区域内CAD模型外的剩余空间.

③ CAD模型到MCNP半空间CSG模型的自动转换.该过程需要完成有界曲面组成的CAD几何体转换为一系列由没有边界的曲面方程组合而成的MCNP栅元.另外，分解后部分CAD模型无法用MCNP半空间CSG模型描述，需要添加辅助面使得半空间CSG模型可描述.

④ MCNP前处理卡片生成.MCNP计算程序使用卡片式数据结构，数据包括：信息部分、栅元卡、曲面卡和数据卡.MCNP前处理相关的数据主要是栅元描述卡和曲面描述卡.栅元描述卡描述计算空间中的几何实体，由一系列曲面描述卡的组合形成的封闭空间，允许采用布尔运算描述几何体.曲面描述卡通过一系列曲面方程描述三维空间中的每一张曲面，其中每张曲面均没有边界，每张曲面均能够通过正负号将整个计算空间分为两部分.

2 应用于MCNP程序的三维模型前处理技术

CAD模型预处理工作包括装配模型到零件模型的转换、模型修复和模型简化.现阶段，模型修复工作主要通过人工交互操作的半自动方法，并没有统一、完备的方法体系，因此CAD模型预处理的关键点为装配模型到零件模型的自动转换方法和模型简化算法.

2.1 CAD装配模型到零件模型的自动转换

CAD装配模型并不包括具体的几何模型，因此需要将装配模型转换为零件模型，用于生成整个MCNP计算空间中的几何对象.在此基础上，才能够顺利进行空腔生成、BRep模型到半空间CSG模型的分解等后续操作.该转换过程可以分为以下3个步骤：

① 以解析装配模型为起点，遍历装配树的每个子节点获取自节点引用的对象并获得该节点的位姿矩阵.如果子节点为装配节点，则递归遍历其子节点并计算每级子节点的位姿矩阵；如果子节点为零件节点，侧获取其引用的几何对象.

② 集合所有子节点的位姿矩阵得到装配模型所有零件在三维空间中的世界位姿矩阵.

③ 根据所有零件节点的几何对象及位姿矩阵，创建新的零件模型，将前面遍历得到的每一个零件中的几何体按照世界坐标中的位姿矩阵进行插入，保存零件模型.通过转换后得到的零件模型不包括原零件模型的建模过程数据.

2.2 CAD模型简化算法

根据CAD模型有无建模过程历史信息，模型简化的算法可以分为两类：基于建模历史的CAD模型简化方法和无历史建模信息的CAD模型简化方法.

2.2.1基于建模历史的CAD模型简化方法

基于建模历史的CAD模型简化算法的主要过程包含3个步骤，分别为细节特征识别、抑制阈值计算以及误差在抑制阀值内的细节特征抑制/删除.误差在抑制阀值内的细节特征抑制/删除为算法的关键，需要实现在指定的误差控制范围内自动识别相应的建模特征并进行特征抑制.文中使用UG NX的CAD模型进行模型简化.

CAD模型存在大量对MCNP计算不重要的生产特征细节，包括尺寸较小的倒角、倒圆角、螺纹和小区域面的拉伸/旋转等特征.识别细节特征分两个方面:一是根据建模历史树中特征的类型和参数识别细节特征，二是将扫略特征中截面形状中尺寸较小的线段作为细节特征.

① 抑制阈值设置.

抑郁阈值主要指细节特征的特征参数以及简化前后模型相异的细节特征列表.抑制阈值的设置是根据具体模型情况确定的，这里给出基于UG的建模特征的细节特征抑制阈值如表1所示.

表1 细节特征抑制阈值列表

② 细节特征识别.

在表1中，倒角、圆角、工艺槽、轴/孔以及扫略特征具有特征值，可以将特征值作为特征对应的抑制阈值.螺纹特征在MCNP计算中不利于粒子输运计算，因此需要将螺纹特征删除，并将螺纹特征的抑制阈值设为TRUE.

③ 误差在抑制阀值内的细节特征抑制/删除.

包含建模过程历史信息的CAD模型的特征存在父子依赖关系.如果后创建的特征是基于已有特征实现的，则将已有特征视为父特征，将后创建的特征视为子特征.父特征节点是子特征节点的定位或其他操作的依据，删除某个父节点特征将使得其所属子节点特征失去参考依据，从而引起模型更新的错误或该节点所有子特征信息的丢失.因此在进行基于建模历史的模型简化时，需要根据特征件的父子关系，判断被抑制特征的父子关系，当某个可被抑制的特征是其他不可抑制特征的父特征时，将该特征从可抑制特征列表中移除.

2.2.2基于BRep数据结构的CAD模型简化方法

无建模过程历史信息的CAD模型只包含BRep拓扑结构和几何信息.这类模型的简化采用基于BRep数据结构的CAD模型简化方法，特征识别和简化均依赖对BRep数据结构的判别和操作，简化过程包括3个步骤：细节特征识别、阀值计算和特征抑制/删除.其中细节特征识别方法和特征抑制/删除算法是基于BRep数据结构的模型简化方法的关键.

① 基于BRep数据结构的特征识别方法.

无建模过程历史的CAD模型主要的细节特征有倒角、倒圆角及工艺槽等，这几类几何细节特征具有类似的拓扑结构，可以通过对几何模型中 BRep 拓扑结构和几何数据的遍历和分析判断出几何细节特征的区域.常用的拓扑元素有体、壳、面、环、边、顶点等.拓扑元素之间的对应关系称为拓扑规则，如面与环之间的对应关系等.几何数据描述是指每个几何组成的数学定义，如曲面的数学方程、控制点坐标等.

根据特征的凹凸性和对应的BRep拓扑结构，可以把细节特征分为7类，如图2所示，对应的特征示例如图3所示.其中倒圆角特征无法通过环的凹凸性进行判别，但倒圆角面通常是圆柱面、圆环面或自由曲面组成.

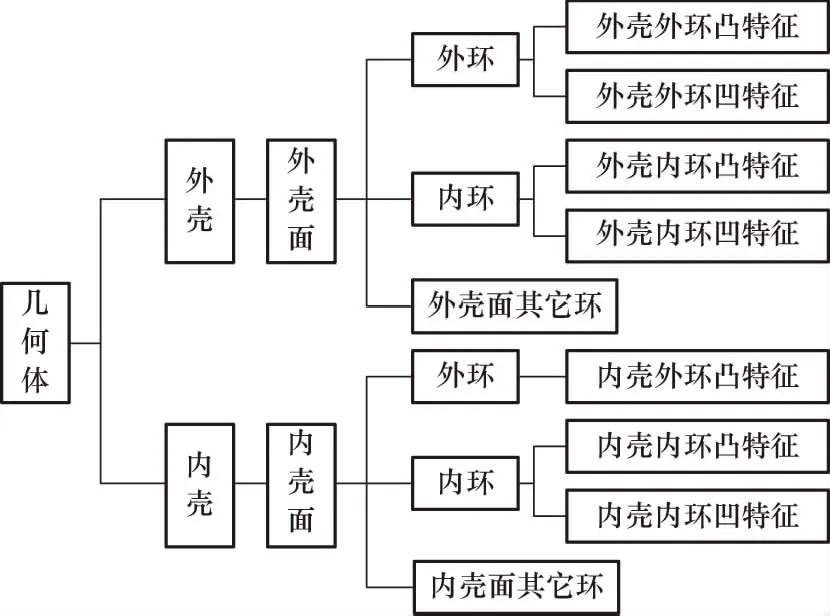
图2 基于壳-面-环的拓扑特征分类

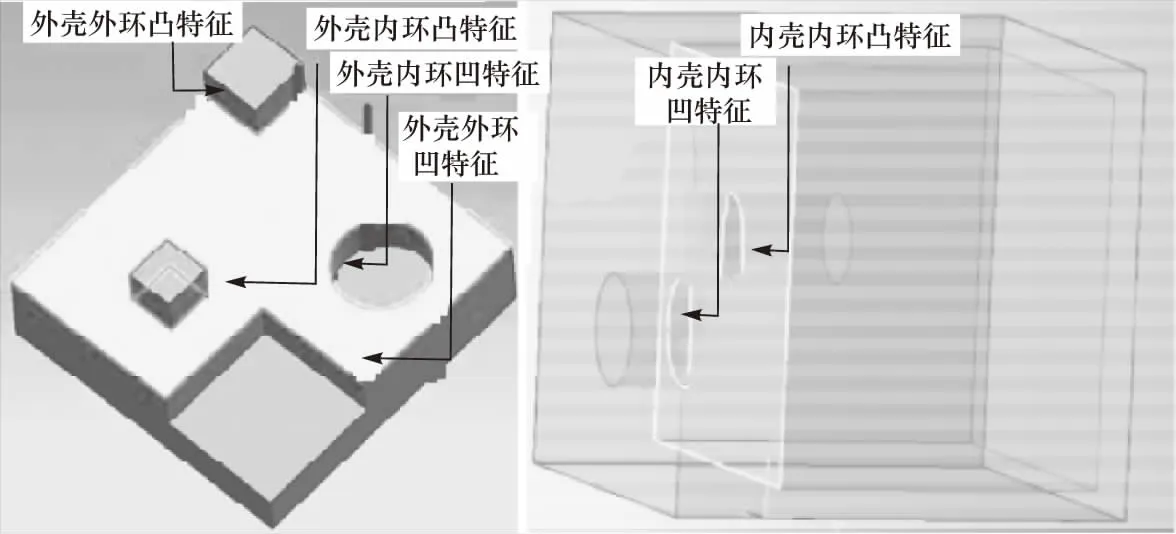
图3 分类特征示例

② 基于BRep数据结构的特征抑制/删除算法.

基于BRep数据结构的特征抑制/删除算法有两种：①先建模辅助几何体，然后进行布尔运算的算法[10]；②直接修改模型拓扑结构实现过渡特征的抑制/删除算法[11].特征抑制/删除时，拓扑结构的修改需要几何开发平台的支持，然而商业CAD开发平台不支持对模型的拓扑结构修改，且同样外形的几何模型具有多种形式的BRep表示方法.因此根据第一种算法设计了基于辅助几何体的细节特征抑制/删除算法.

算法分为两个阶段.首先自动构造辅助几何体，根据特征识别的结果来构造需要增加或去除的空间区域.然后进行辅助几何体和待简化模型的布尔运算.此处的布尔运算采用“布尔加”和“布尔减”两种操作.其算法的实例如图4所示.

图4 基于辅助几何体的细节特征简化算法实例

3 基于区域层次分割的空腔生成算法

MCNP计算模型需要完全定义整个问题空间，需要对问题空间内的空腔区域(即几何实体之外的空间)进行三维建模.常规的空腔生成使用整个计算空间的包围盒布尔减运算所有的几何实体[6]，该方法存在两个缺点：其一是计算成本高并且计算时间长；其二是模型结构复杂时布尔运算的成功率低.因此，文中提出基于区域层次分割的空腔生成算法，该算法将布尔运算转换为逻辑运算，降低了计算成本和时间，提高了空腔生成的成功率.

算法以CAD模型输入作为起点，人工定义计算区域.然后基于确定的计算区域可直接生成CAD模型外部的空腔区域，并输出外部空腔模型；CAD模型内部的空腔区域生成则按照如下过程进行：①获得所有零件模型的几何实体；②进行邻接几何体聚类分析，划分邻接几何体区域；③判定几何体区域的类型，形成层次区域树；④根据层次区域树，进行几何体区域的逻辑求余；⑤输出内部空腔模型.

4 基于空间分解的CAD模型到MCNP半空间CSG模型转换

商业CAD模型向MCNP半空间CSG模型的转换本质上是BRep描述到半空间CSG描述的映射.BRep表示方法中，物体由有限个面构成，每个面则为有限条边围成的有限个封闭域定义，即物体的边界是有限个单元面的并集，且每一个单元面也必须有界.CSG表示方法采用无界曲面作为空间划分的基础.首先通过任意一张曲面把全部几何空间分割为两个部分(正半空间和负半空间)，然后通过多张曲面半空间CSG区域的布尔运算组合描述几何形体.BRep模型到半空间CSG模型的映射具有以下特点：

① 一个CAD实体模型可以有多种半空间表示方法.

② 任意复杂CAD实体模型难以直接转换为某种形式的半空间表示.

③ 部分CAD实体模型仅采用自身的曲面信息无法得到正确的半空间描述，需要添加辅助面才能得到半空间CSG可描述.

根据以上分析，基于空间分解的CAD模型到半空间CSG模型转换涉及两个关键问题：

① CAD模型分解，把复杂的 CAD 模型转换为一系列简单的实体组合.

② 半空间不可描述实体模型判断及其辅助面生成.

基于空间分解的CAD模型到MCNP半空间CSG模型转换涉及新的概念，本章节首先对概念进行定义，接着在此定义上设计模型转换算法.

4.1 定义

定义1半空间转换元：满足如下条件的三维实体称为半空间转换元.

① 如果有界曲面A属于该三维实体，则该三维实体内的任意点均位于无界曲面B的同一侧，无界曲面B是未经裁减的有界曲面A；

② 该三维实体是正则形体.

定义3不完全半空间转换元：半空间转换元中所有不属于完全半空间转换元的被称为不完全半空间转换元.

定义4半空间辅助面：对于一个不完全半空间转换元D，存在一个或多个曲面f，如果f满足如下条件则曲面f被称为该不完全半空间转换元D的半空间辅助面.

① 不完全半空间转换元D中的任一点位于曲面f的同一侧；

② 曲面f包含一条或两条不完全半空间转换元D的边界曲线；

③ 不完全半空间转换元D中的曲面与曲面f的半空间组合空间区域小于仅由不完全半空间转换元D中的曲面半空间组合形成空间区域.

可以证明，对于一个不完全半空间转换元D，如果D中包含n张二阶以上曲面，则最多需要添加的半空间辅助面不超过n个.

4.2 基于空间分解的CAD模型到MCNP半空间CSG模型转换算法

根据4.1中的定义，基于空间分解的CAD模型到MCNP半空间CSG模型转换算法的技术框架如图5所示.首先通过区域划分将整个计算空间划分为多个简单区域的组合，划分区域内的CAD模型几何体作为该区域的子节点，并根据区域划分结果利用章节3中的算法生成整个计算区域的空腔；接着对每个几何体进行分解面构造，通过分解面把CAD模型进行半空间分解，使一个CAD模型转换为一系列半空间转换元的组合.算法的技术路线如下：

图5 基于空间分解的CAD模型到MCNP半空间CSG模型转换算法

① 判断需要分解的CAD几何实体C是否是半空间转换元，如果是，分解结束；否则进入步骤②；

② 根据实体C中的拓扑特征和曲面信息构造某个合适的分解曲面f，分解曲面f把C分解为两个或多个几何实体C1，C2，…，Cn；

③ 分别对C1，C2，…，Cn进行第一步操作，递归分解直至得到所有半空间转换元.

分解曲面不同，分解的结果和效率完全不同，因此可以根据CAD模型的拓扑结构，把CAD模型分为如图2所示的7类特征.转换算法对于不同的特征，采用不同的分解方法.

4.2.1不完全半空间转换元辅助面添加

不完全半空间转换元必须添加辅助面才能被MCNP正确描述.由于平面具有描述简单、求交迅速以及易于空间分割等优点，优先采用平面作为需要添加的辅助面类型.首先对得到的每一个半空间转换元进行判别，如果是完全半空间转换元，则可以直接得到其半空间转换表达式.对于不完全半空间转换元，首先通过辅助面生成算法，得到该不完全半空间转换元的最优半空间辅助面，然后通过最优半空间辅助面和该不完全半空间转换元的所有曲面集合得到其半空间转换表达式.图6是几种典型的不完全半空间转换元及其需要添加的辅助面.

图6 几种典型的不完全半空间转换元及其需要添加的辅助面

4.2.2MCNP前处理卡片生成

由于CAD实体中的曲面为有界曲面并且CAD实体中的曲面法向恒指向实体外部，导致CAD中的曲面与MCNP半空间曲面不一致，一系列CAD实体中的所有曲面转换为MCNP半空间曲面描述时，存在MCNP半空间曲面重复，并且必定存在MCNP位置相同但方向相反的半空间曲面对的问题.为此，必须进行曲面归并，即把所有曲面方程一样或方向相反的所有CAD曲面作为同一张MCNP半空间曲面.曲面卡生成算法按照如下步骤：

①曲面识别；②曲面信息提取；③MCNP曲面方程构造；④曲面归并.对于每一个完全半空间转换元，根据其中每一曲面对应的曲面卡和方向构造出栅元卡.

5 实例验证

文中依据应用于MCNP程序的三维模型前处理技术，在NX平台上开发实现了MCNP三维前处理软件，并采用该软件实现了多个包含数千几何体的复杂结构核设施的MCNP三维前处理建模，大幅提高了建模效率.应用效果表明，基于区域层次分割的空腔生成方法可以减少空腔部分70%以上的栅元数量，前处理效率和MCNP粒子输运求解时间均大幅降低.

CAD模型转换的过程和结果如图7所示，图中展示的是无区域层次分割的空腔生成方法.图7(a)是CAD模型，图7(b)是自动生成的空腔模型，图7(d)是分解后的半空间转换元，图7(e)是图7(d)中的不完全半空间转换元及建立的辅助面，图7(c)是空腔分解后的半空间转换元，图7(f)是空腔转换后的所有不完全半空间转换元及建立的辅助面，图7(g)是转换后的MCNP INP文件在其二维可视化工具vised上的验证效果，转换结果完全符合 MCNP输入文件格式的几何模型描述.

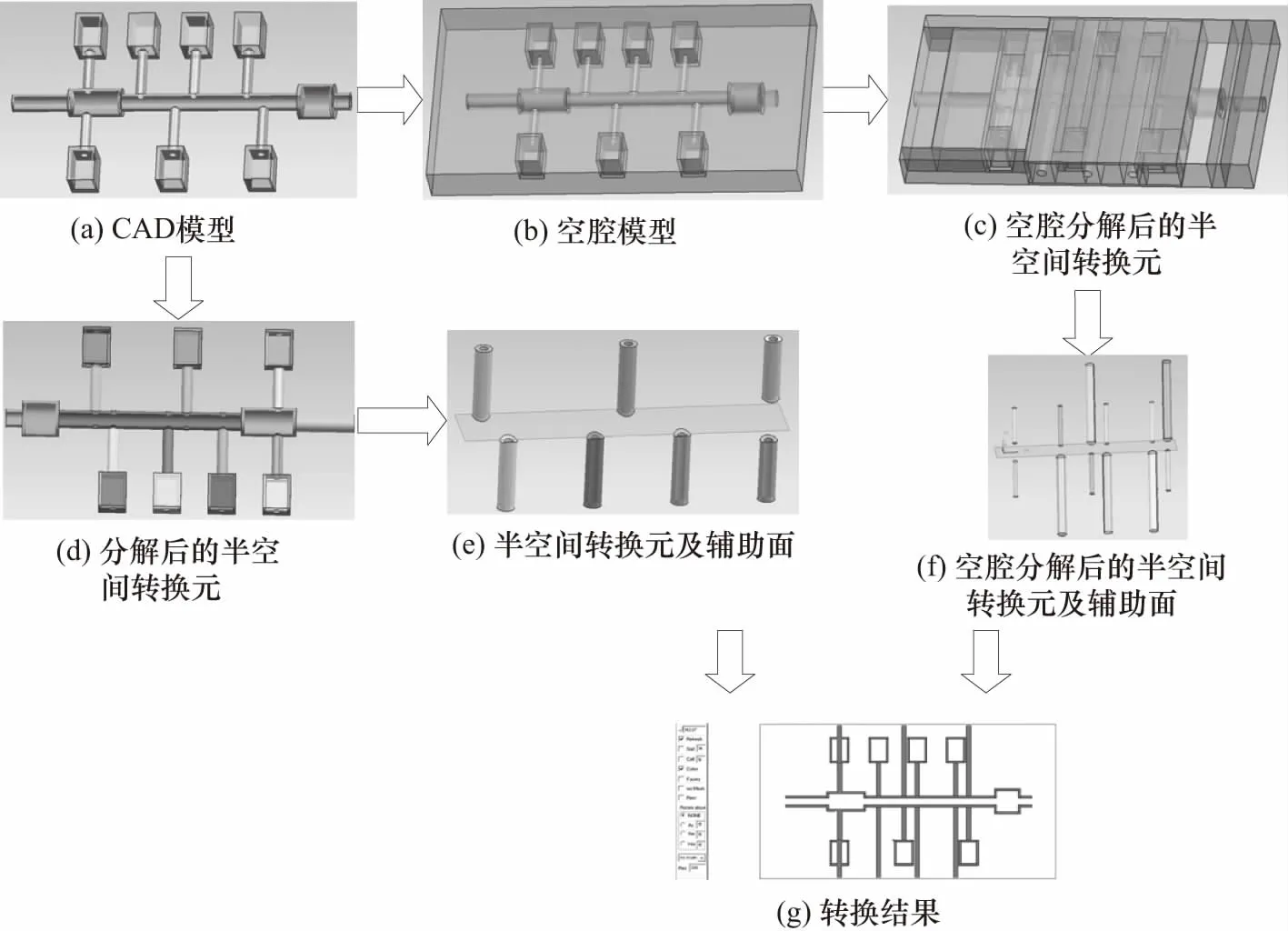
图7 CAD模型转换效果实例

上述算列如果采用基于区域层次分割的空腔生成方法，则图7(e)中的栅元可以简单描述为图7(b)中的外围包围盒对图7(c)中的所有栅元的补集，这样就可以减少图7(e)和图7(f)的计算和操作开销.需要注意的是，MCNP求补运算支持的最大的栅元个数是有限制的(如MCNP5最大支持不超过100个栅元的求补).当超出最大支持的栅元个数时，需要采用区域层次分割的方法定义一系列区域，形成区域的嵌套关系.最终大区域内可以包含多个小区域，但每个区域内的栅元个数不超过MCNP支持的最大求补数量.

6 结束语

文中研究了应用于MCNP程序的三维模型前处理技术，通过CAD模型识别与简化算法、空腔生成算法以及CAD模型向MCNP半空间CSG模型转换算法可高效地实现三维CAD模型向MCNP半空间CSG模型的转换，并可快速地生成MCNP程序使用的数据文件.通过实例验证了文中方法的高效性和可靠性.