T型三撑杆索穹顶预应力计算方法与参数分析
张爱林, 武超群, 张艳霞
(1.北京建筑大学 土木与交通工程学院,北京 100044;2.北京建筑大学 北京未来城市设计高精尖创新中心,北京 100044)
索穹顶结构基于美国建筑大师FULLER[1]在20世纪40年代提出的张拉整体体系,他设想在结构中尽可能地减少受压构件,从而使结构处于连续的张拉状态和间断的受压状态,使“压力成为拉力海洋中的孤岛”。国内外学者提出多种索穹顶构造[2-5],构造形式多为单一图形的复制。索穹顶结构网格划分均匀,但传力路径复杂,对索穹顶结构索、杆初始预应力的分析缺少考虑三维方向的理论计算公式[6-8],还存在缺少对索穹顶结构工程应用考虑的问题。
我国索穹顶结构研究起步虽晚,但近年来,在国家政策的大力倡导下,索穹顶结构研究在国内备受关注,我国学者先后提出Kiewitt型索穹顶、鸟巢型索穹顶和蜂窝四撑杆型索穹顶等[9-10]新型索穹顶结构体系,并提出确定初始预应力分布的简捷计算方法。在工程实践应用方面进行了诸多实践探索及施工技术[11]的创新,2009年成功建造第一座自主设计和施工的24 m跨度的无锡科技交流中心索穹顶,之后中国煤炭交易中心索穹顶和内蒙古伊金霍洛旗体育中心索穹顶相继竣工,标志着我国索穹顶研究计算理论和实际工程结合的飞速进步。因此,对索穹顶结构的创新研究及性能研究是现代大跨度空间钢结构领域的重要课题,既符合学科前沿发展趋势,也符合国家重大工程需求,具有广泛的应用前景。
基于目前索穹顶结构存在的构造形式单一、环向刚度较差等问题,对索穹顶结构形式改变及环向刚度提升进行创新研究。
1 T型三撑杆索穹顶结构形态分析及构造特点
提出一种新型索穹顶结构——T型三撑杆索穹顶,如图1所示。T型三撑杆索穹顶结构由环索、脊索、斜索、撑杆及刚性环梁组成。与传统Geiger型、Levy型索穹顶相比,T型三撑杆索穹顶将竖直的撑杆变为三根斜向撑杆,由三根斜撑杆组成的四面体单元重心靠近索穹顶内侧,由索穹顶中心到外圈布置三撑杆单元,增加了结构稳定性。内圈三撑杆单元紧密相连,在环向上形成撑杆环,外圈三撑杆布置在内圈2个三撑杆单元相连方向,外圈三撑杆单元由交错的双撑杆单元相连,且与内圈由多根脊索相连,提高了结构的环向刚度和径向刚度,增加结构抵抗非均布荷载的能力。图1(b)中可见,该结构网格划分均匀,可划分为6个单元,结构整体性好。相较于传统的索穹顶结构,T型三撑杆索穹顶撑杆环向连接紧密,结构环向刚度大,结构网格划分均匀,施工难度小。该结构避免了Geiger型索穹顶环向刚度不足的情况,同时也避免了Levy型索穹顶由于结构构件数量多、施工张拉难度大、节点设计困难的问题。
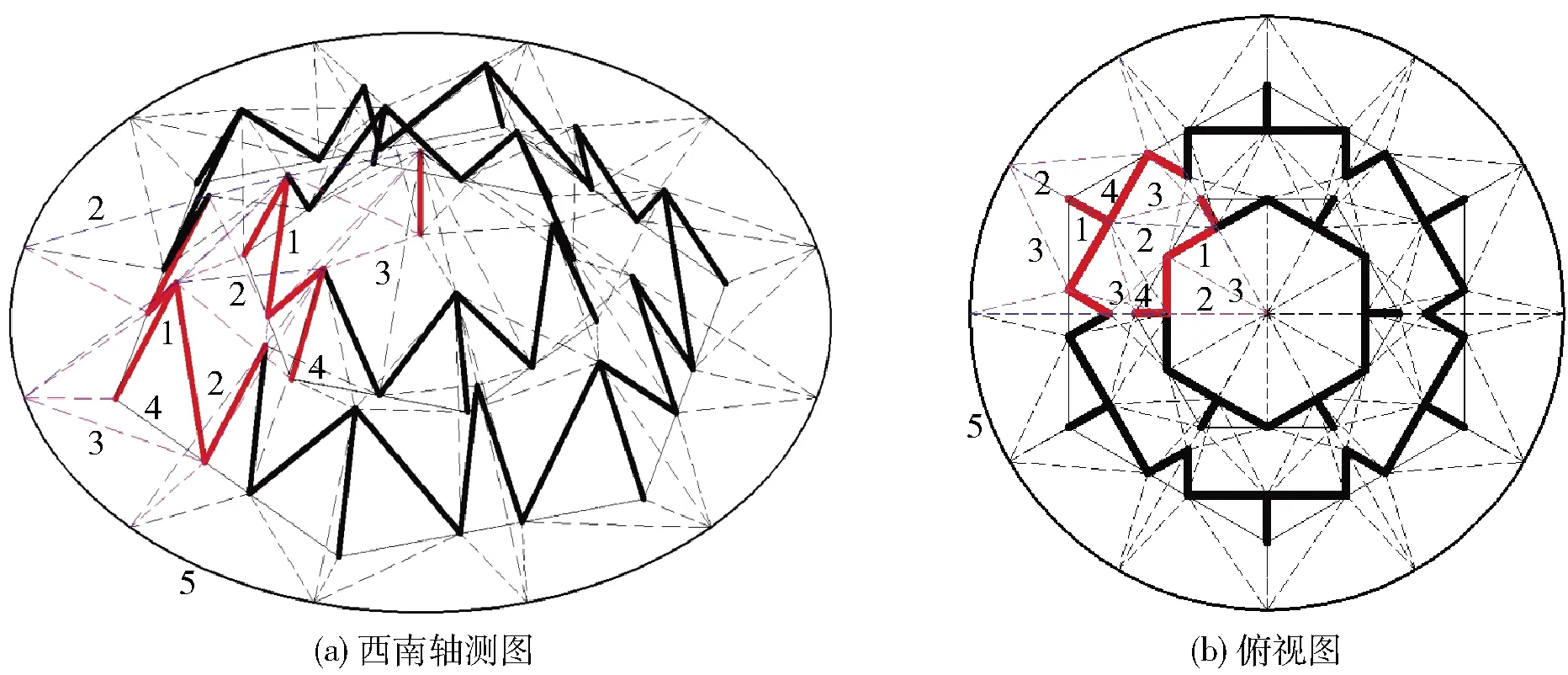
注:1.撑杆;2.脊索;3.斜索;4.环索;5.刚性环梁
2 T型三撑杆索穹顶预应力分析
2.1 计算单元选取
T型三撑杆索穹顶结构为沿30°角的对称结构,即沿平面图中内圈脊索的延长线对称,取1/6结构单元进行分析,如图2(a)所示,其沿内圈脊索角平分线对称,对称面两侧索杆布置相同预应力以及外荷载,因此仅需研究其1/6结构的半榀即可,取1/12结构作为计算单元,如图2(b)所示。索穹顶结构外围设置有足够大刚度的刚性环梁,其与索穹顶的连接可按固定铰支座考虑,结构计算简图如图2(c)所示。

图2 1/12计算单元简图
T型三撑杆索穹顶结构平面与剖面计算简图如图3所示,图中各参数含义为:Ci、Ji(Ji′)、Xi(Xi′)、Hi分别为撑杆、脊索、斜索和环索内力,i(i′)为节点编号,αi为脊索与水平面的夹角,βi为斜索与水平面的夹角,ξi为经过交点的撑杆与水平面形成的夹角,ψi,i-1为由节点i与节点i-1形成的撑杆或索与对称轴线的夹角,hi和hi′为节点i和节点i′所在的水平面相对于节点i+1所在的水平面的高度差,Gi为索、杆自重(其值为与节点相连所有构件及节点自重的1/2)。
2.2 初始预应力计算公式推导
根据图3所示的几何关系,可求得各索、杆与水平面的夹角,以及与对称轴线之间的夹角等。以索穹顶中心撑杆的实际内力C0为基准,利用节点平衡法(其中按照压力方向计算,所有的力均为正值)推导0、0′节点对应的各索、杆的内力,见式(1)和式(2):
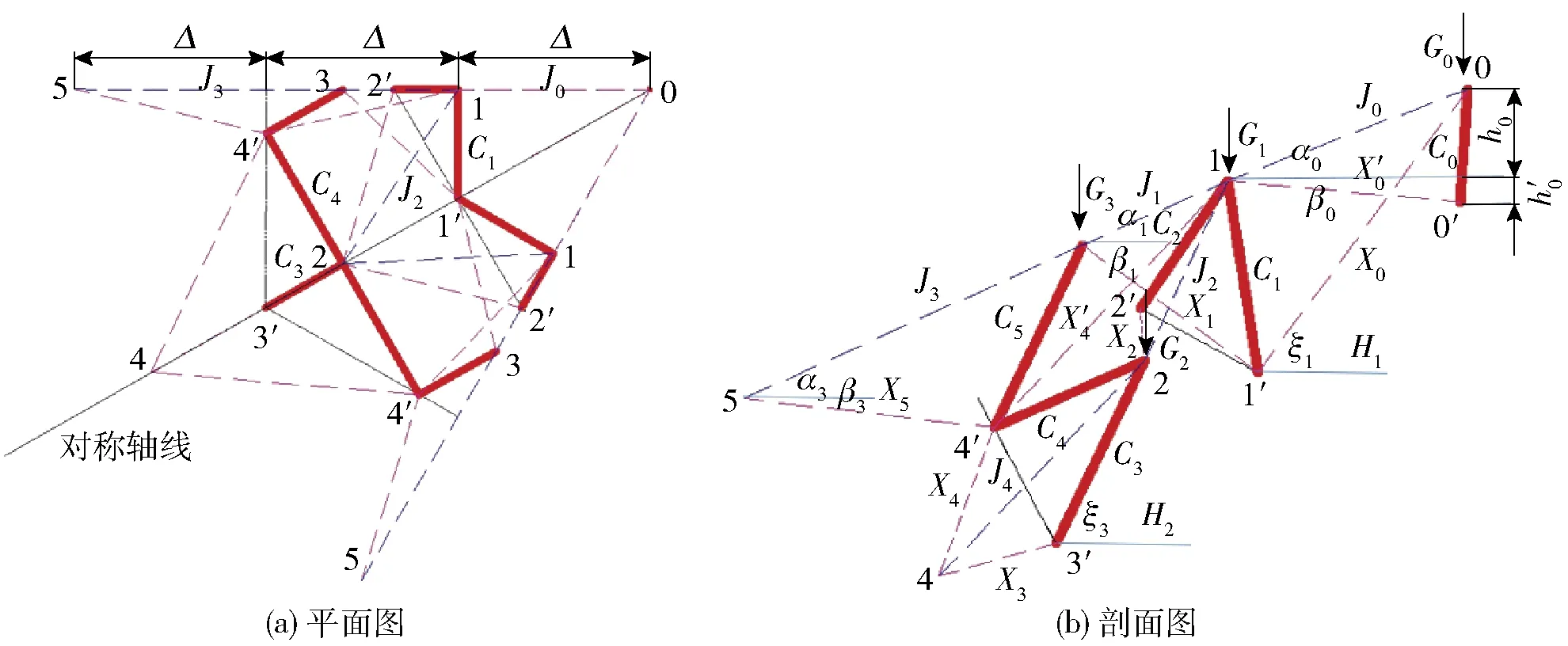
图3 T型三撑杆索穹顶结构平面与剖面计算简图
节点0:
6J0sinα0+6X0sinξ0=C0-G0
(1)
节点0′:
6X0′sinβ0=C0+G0′
(2)
由于在节点0、0′处1个节点均最多有2个未知力,可运用节点平衡法求解,斜索X0由式(9)求得,但在节点存在多个未知力,铰接于节点1的构件有2根撑杆、3根脊索、1根斜索,共6个构件,之前节点平衡求得脊索J0、斜索X0′,已知节点自重G1,剩余4个未知量无法直接求解,属于超静定问题。结合求解平面超静定刚架内力的方法,采用结构力学位移法进行索、杆预应力求解,以节点位移作为基本未知量,通过位移方程和已知外力,求出节点位移,进而推出索、杆内力。
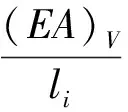
(3)
式中:kxx、kyy、kzz分别为分析单元在x、y、z方向上产生单位位移时索需要的力;kx(y,z)、ky(x,z)、kz(x,y)分别为当一个方向产生位移时,对另外一个方向的影响;Δ1x、Δ1y、Δ1z为已知索、杆在沿x、y、z轴方向上的单位位移;F1x、F1y、F1z为已知索、杆预应力沿轴、轴、z轴上的分力,求解见式(4)(其中斜索X4′由节点4’求得,此处视为已知力)。式(3)仅适用于对称结构受均布荷载。
(4)
由于结构在成形后刚度足够大,节点1在外力作用下产生的节点位移较小,可忽略当x(y,z)方向产生位移时对y(x,z)、z(x,y)的影响,即kx(y,z)=ky(x,z)=kz(x,y)=0。式(5)为索、杆刚度,式(6)为单元刚度。
(5)
(6)
将式(4)~(6)代入式(3)可得节点1的沿x轴、y轴、z轴的位移,见式(7)。
(7)
则索、杆的实际内力为式(8)。
(8)
在节点1′处,有2根撑杆、3根斜索、1圈环索与节点1′相连,已知节点自重G1′和撑杆C1,因环索H1为水平力且二力平衡,则利用节点平衡法即可求得斜索X0、斜索X1内力,见式(9):
(9)
节点2′同理,可由z轴方向的节点平衡求得,则利用节点平衡法即可求得斜索X2、环索H1内力,见式(10):
(10)
节点2属于超静定问题,需采用位移法求得各索、杆内力,见式(11)~(15):
(11)
(12)
(13)
(14)
(15)
节点可利用节点平衡法求得撑杆C5、脊索J3内力,见式(16):
(16)
节点3′同理,斜索X3可由z轴方向的节点平衡求得,则利用节点平衡法即可求得斜索X3、环索H2内力,见式(17):
(17)
节点4′可利用节点平衡法即可求得斜索X4、斜索X5、斜索X4′内力,见式(18):
(18)
通过以上各公式即可求出T型三撑杆索穹顶中的所有索、杆内力。
3 影响初始预应力的参数分析
3.1 矢跨比的影响
理想预应力下与实际预应力下索穹顶索、杆预应力变化趋势一致,仅考虑理想预应力,采用控制变量法改变索穹顶结构撑杆高度、矢跨比,分析索穹顶初始预应力变化情况。
T型三撑杆索穹顶结构简化半榀平面桁架如图4所示。撑杆下节点在水平面的投影分别在脊索水平面投影的1/3和2/3处且交替布置,各环索在水平面投影的间距相等均为Δ,为简化计算令hα=hβ。由几何关系可求得αi,βi,ξi等,具体计算见式(19),改变矢跨比,取f/L0值为1/20、2/25、1/10、3/20,对撑杆C0施加单位内力,赋值为6,将式(19)带入式(1)~(18)可得到各索、杆内力,求得初始预应力的计算结果见表1。
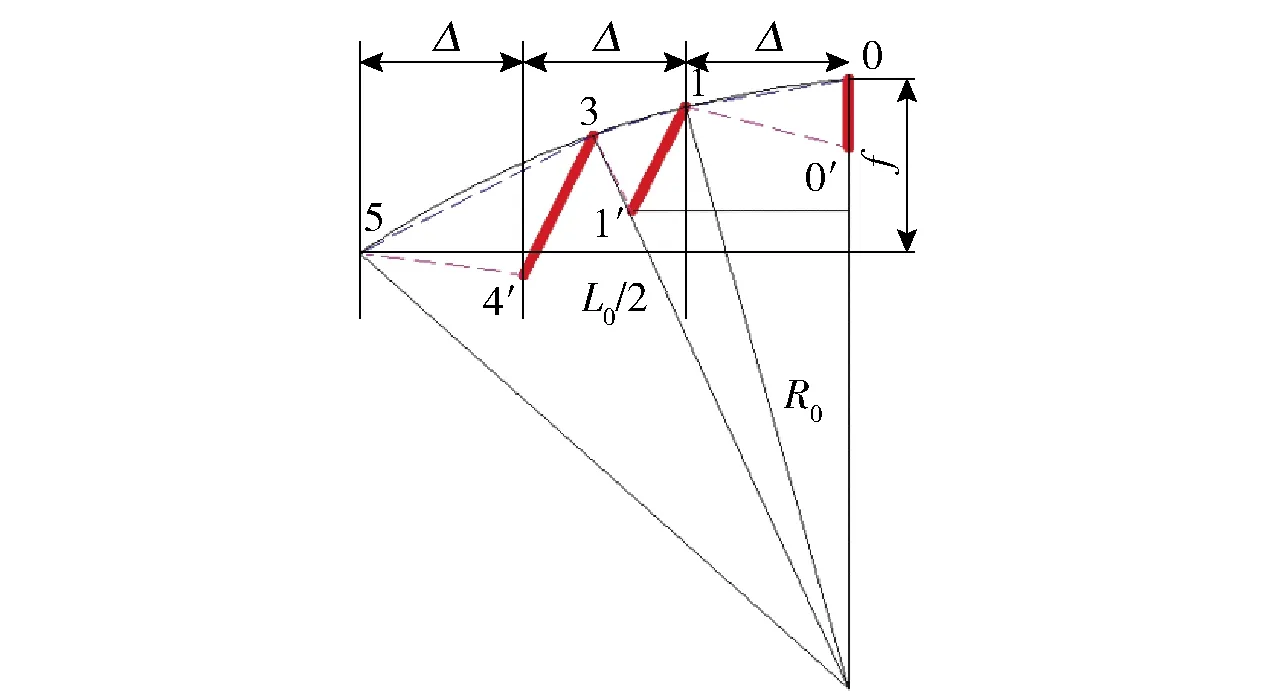
图4 结构简化半榀平面桁架简图
(19)
3.2 撑杆高度的影响
固定结构矢跨比为1/10,研究撑杆高度对索穹顶结构内力分布的影响。保持脊索在x0y平面投影依然为Δ,其他几何参数与不同矢跨比下参数保持一致。hα已由式(19)求出,则撑杆高度由hβ控制。分别取hβ=Δtan 10°、hβ=Δtan 15°、hβ=Δtan 20°,对撑杆C0施加的单位内力赋值为6,由式(1)~(18)可得各索、杆预应力分布情况,其计算结果见表2。
对比表1、表2可知,在一定范围内,矢跨比越大,索、杆初始预应力越小;撑杆高度越大,索、杆初始预应力越小,即T型三撑杆索穹顶索、杆初始预应力与矢跨比、撑杆高度均成反比,并且内圈杆件初始预应力变化幅度小于外圈。通过计算推导可知,在理想状态下(不考虑自重),当hβ>tan 20°或f/L0>3/20时,部分构件会出现失效,则T型三撑杆索穹顶结构适宜矢跨比为1/20~3/20,适宜撑杆高度为斜索角度tan10°~tan20°时的取值。

表1 不同矢跨比下T型三撑杆索穹顶初始预应力

表2 不同撑杆高度下T型三撑杆索穹顶初始预应力(hβ)
4 结 论
本文针对传统索穹顶构造形式缺乏创新及受力性能中环向刚度弱的问题,提出一种T型三撑杆索穹顶。对于新型索穹顶索、杆初始预应力计算缺乏考虑三维方向的推导计算公式,基于结构力学求解超静定问题的方法,提出一种索穹顶索、杆初始预应力计算方法,并通过控制变量法研究矢跨比、撑杆高度对T型三撑杆索穹顶初始预应力的影响。其结果表明:
1)T型三撑杆索穹顶由索穹顶中心到外圈共布置2层三撑杆单元,增加了结构稳定性。内圈三撑杆形成的单元紧密相连,在环向上形成撑杆环,外圈三撑杆单元与双撑杆单元交错相连,且与内圈由多根脊索相连,提高了结构的环向刚度,增加了结构抵抗非均布荷载的能力。T型三撑杆索穹顶结构有效改善索穹顶构造形式单一的问题,并且具有较高的承载能力。
2)提出索穹顶索、杆初始预应力计算方法,考虑三维方向,将索、杆投影到x0y平面、y0z平面、x0z平面,结合求解平面超静定刚架内力的方法,采用位移法进行索、杆预应力求解,以节点位移作为基本未知量,通过位移方程和已知外力,求出节点位移,进而计算得到索、杆内力。
3)矢跨比及撑杆高度对于T型三撑杆索穹顶索、杆初始预应力的影响均为负向,即增大矢跨比或增加撑杆高度,都会使索、杆初始预应力减小,并且内圈索、杆初始预应力变化幅度小于外圈。T型三撑杆索穹顶结构适宜矢跨比为1/20~3/20,适宜撑杆高度为斜索角度tan10°~tan20°时的取值。

