电磁感应下胰腺β细胞的放电及同步分析

李 宁，李新颖，杨腾云

(1. 兰州交通大学 数理学院，甘肃 兰州 730070；2. 兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

神经系统是由千千万万的神经元组成非常庞大同时又非常复杂的信息网络系统，直接或间接地调节和控制人体内的各个器官、系统功能和各种生理过程，具有极其复杂的动力学行为. Chay和Keizer[1]刻画出第一个内分泌腺体细胞的模型，它解释了电生理实验中胰腺β细胞出现的振荡现象和分泌胰岛素的行为. 胰腺β细胞的主要功能是分泌胰岛素，以此调控血液中的葡萄糖浓度. 细胞外葡萄糖浓度的增加会导致胰腺细胞产生放电活动[2]. 细胞膜的异常放电可能会导致胰岛素分泌紊乱，进而导致Ⅱ型糖尿病的发生[3]. 因此，对胰腺β细胞的研究变得尤为重要.

根据β细胞的不同特性及细胞膜上的各种离子通量，可以将胰腺β细胞划分成许多模型. 杨卓琴等[4]对phantom簇放电模型进行分析，研究了2个电耦合胰腺β细胞的同步行为，同时利用快慢动力学分析了不同时间尺度对簇放电行为的影响. 刘深泉等[5]对Sherman模型进行同步研究，结果表明，改变耦合强度和慢时间常数都可以引起复杂的同步状态转迁变化. 由于神经元离子通道电流在细胞膜上的交换不仅仅只产生了膜电位，还产生了电磁感应[6]. 因此在对于神经元生物电的进一步研究中，于浩等[7]在chay神经元上加入忆阻器电流，发现磁流作用下神经元表现出复杂混合振荡模式. 文献[8]考虑在改进FHN神经元模型的基础上引入电磁辐射，对神经元电活动的动力学行为进行了分析和讨论，证实了在不同的电场下会引起神经元电活动的不同模态跃迁. 文献[9]对改进HR神经元模型引入电磁辐射，通过检测外界电磁辐射作用下对神经元内电活动的模态跃迁，发现电磁辐射既能刺激静止神经元，又能抑制神经元的电活动.乔帅等[10]对磁通e-HR神经元的放电及分岔模型进行研究，发现该模型具有隐藏放电行为. Ma等[11]考虑电磁感应，在改进HR神经元模型的基础上研究了同步相位的逼近问题，结果表明，神经元间的磁通耦合可以实现理想的相位同步. 但是对于磁通耦合神经元的完全同步行为还有待研究.

本文在Sherman模型的基础上，添加忆阻器，建立由忆阻器实现神经元的磁通量与膜电位之间耦合的四维神经元模型. 不仅对单个磁流作用下胰腺β细胞的放电特性进行了单参数分析与二维参数平面的双参数分析，发现电磁感应下胰腺β细胞存在加周期分岔、逆加周期分岔与倍周期分岔之间相互转换，呈现静息态-周期峰-混沌-周期簇放电模式的转迁；而且还对磁通耦合的胰腺β细胞模型基于同步差原理分析了该系统达到同步状态时的条件，同时通过数值模拟了不同参数变化时系统的完全同步情况.

1 模型描述

Sherman等于1988年利用神经元HH模型的方法，建立了一个相对简单但是具有代表性的簇放电胰腺β细胞模型. 忆阻器可以用来描述横跨膜磁通量的大小，通过加入忆阻器与外部电刺激来研究神经元胰腺β细胞的放电活动，其方程如下:

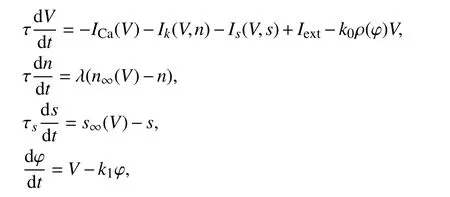
2 单参数对电磁作用下胰腺β细胞的放电模式的影响

2.1 反馈增益 k1对放电模式的影响神经元膜电位的变化可以在系统的周围媒介中产生磁场[14]，k1表示电磁感应中产生的电流对膜电位影响的反馈增益[15]. 首先研究负反馈-k1φ中的k1对系统膜电位的影响.固定参数k0=0.05，α=2，β=0.000 5，当k1变化时神经元会表现出不同类型放电模式. 图1显示了电磁感应下不同k1值时胰腺β细胞的放电模式.

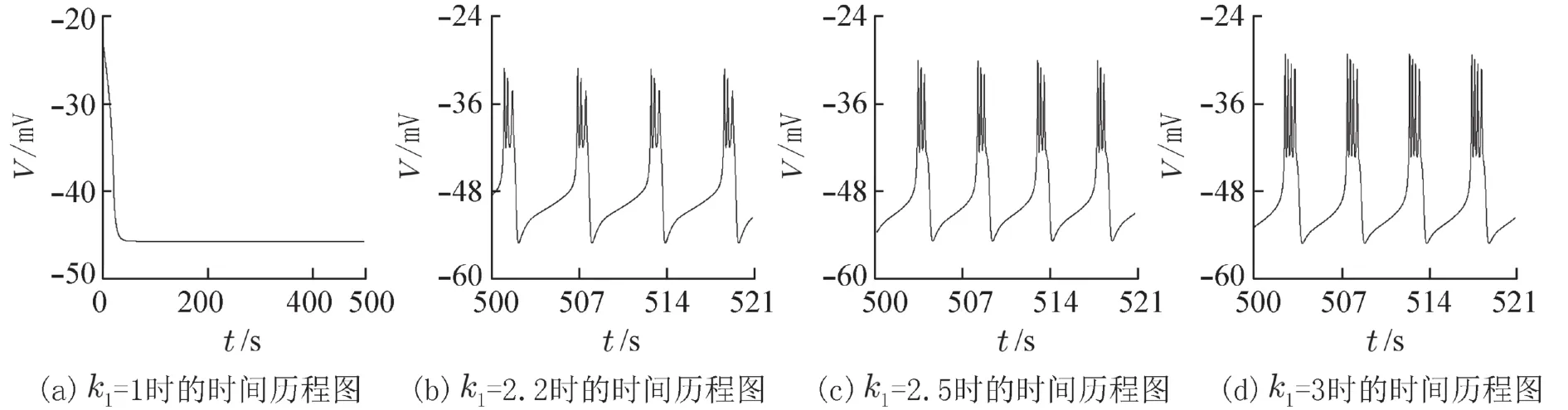
图1 不同 k1 时电磁作用下β细胞的放电模式Fig. 1 Discharge modes of beta cells under different electromagnetic fields underk1

当k1=1时，膜电位振荡的幅值很小，系统处于静息状态；当k1增加到2.2，2.5时，系统呈现出3周期簇放电，随着k1的值进一步增大到3时，系统呈现出4周期簇放电模式. 说明胰腺β细胞在电磁感应的作用下，改变增益k1的值，神经元系统的放电由静息态被激发转变为周期簇放电.

在神经元中，除了倍周期分岔，还经常会出现加周期分岔现象，系统放电节律的周期数每次以加1的方式变化[16]. 图2是峰峰间期随参数k1变化的分岔图，图2(b)是2(a)中k1∈(2.4,3) 的局部放大图. 随着k1的增加，系统由2周期放电发生了倍周期分岔为4周期，然后由4周期逆倍周期分岔到2周期，接着又经历了加周期、逆加周期和加周期分岔最终达到4周期簇放电模式. 从图2中可以看出随着k1的增加，系统不同类型的放电模式之间是通过倍周期分岔、逆倍周期分岔、加周期分岔和逆加周期分岔进行转变的.

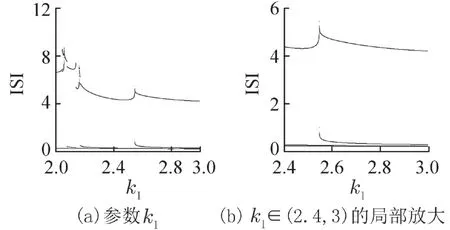
图2 关于参数 k1 的峰峰间期分岔图Fig. 2 The ISI bifurcation diagram with respect to parameter k1

2.2 外部电刺激对放电模式的影响神经活动中神经元起着传递信息的作用，从其他的突触接受信号. 在神经元传送信号中添加适当的外部电刺激，则会使细胞的膜电位发生改变，造成信息编码的方式改变，进而影响神经系统的动力学行为[17]. 因此下面对参数Iext进行研究，分析其对于膜电位产生的影响.

如图3（a）～（h）所示. 当Iext=-5 mA时，系统呈现1周期峰放电模式，随着外部电刺激的增加；当Iext=-4.3 mA时神经元系统出现混沌现象；Iext=-1.2,0.4 mA时，系统恢复为稳定的2，3周期簇放电模式.从图3中可以看出，神经元系统随着外部电刺激Iext的改变完成由峰放电到混沌再到簇放电的转迁，说明Iext的改变丰富了系统放电活动.

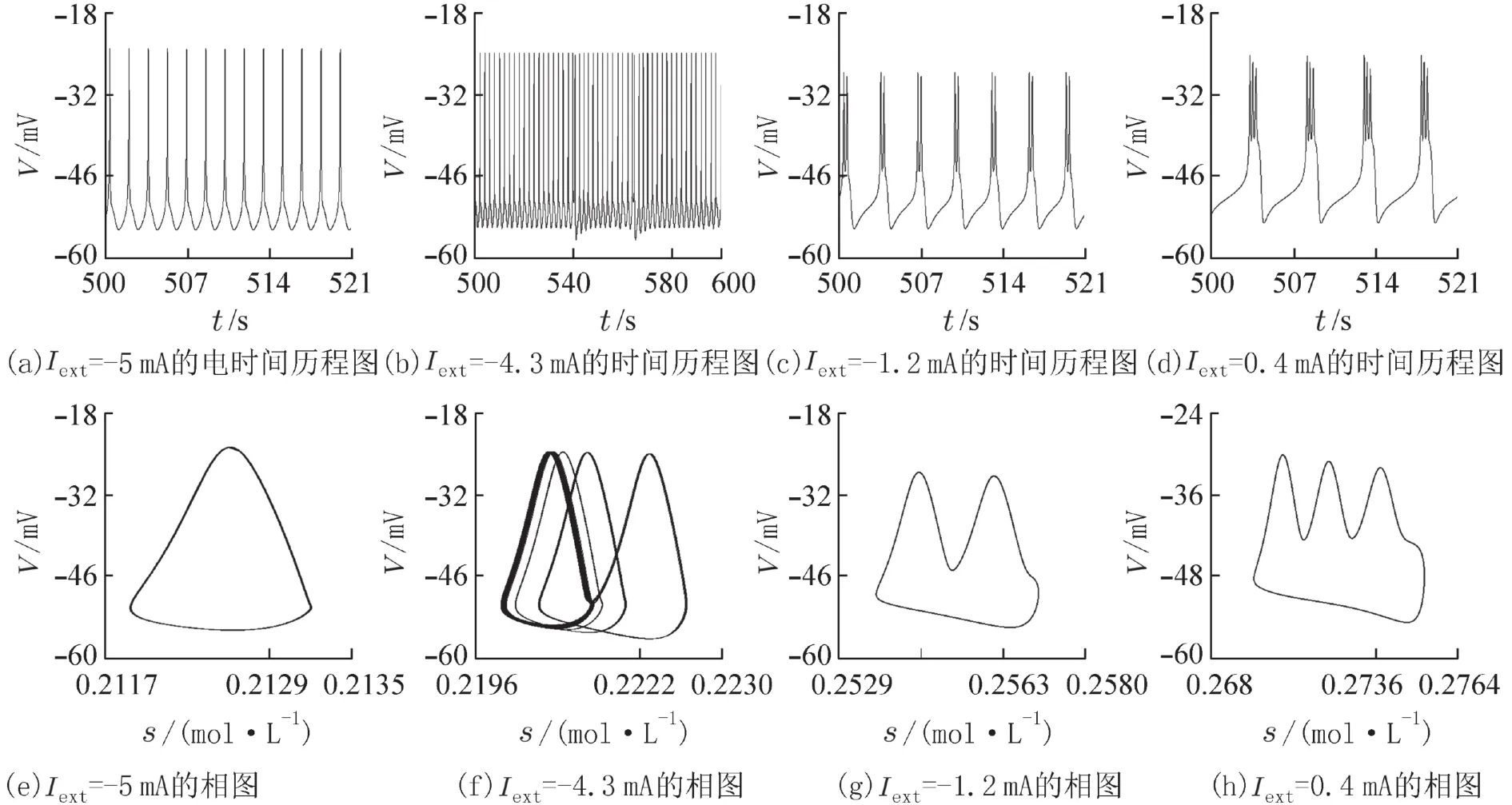
图3 不同Iext 时电磁感应β细胞的放电模式Fig. 3 Discharge modes of beta cells under electromagnetic fields under differentIext

图4是峰峰间期随外部电刺激Iext的分岔图，Iext的改变使得系统的放电模式更加丰富. 随着参数Iext从-5增加到-3，系统从1周期峰放电倍周期分岔到2周期峰放电，在参数很小的变化下系统激发进入混沌，随着Iext的取值逐渐增大，混沌放电退化为4周期峰放电、混沌状态、3周期峰放电、5周期峰放电放电状态；系统一直重复周期-混沌-周期的放电模式. 当Iext∈(-3,1) 系统转为稳定的加周期分岔状态呈现出2周期、3周期、4周期，但最后又经过逆加周期分岔，下支的分岔消失，4周期簇放电退化为稳定的3周期簇放电放电.

反馈k1与外部电刺激Iext的改变都使系统呈现丰富放电模式. 但是Iext的改变，使系统呈现出周期峰放电和混沌放电模式，比反馈k1更丰富了系统的放电模式.

图5为外部电刺激Iext与反馈增益k1为分岔参数的双参数分岔图. 双参图中不仅可以呈现单参数的分岔情况[17]，而且能够从图中清晰地看出2个参数同时变化时神经元系统所展现的丰富动力学行为.

图5中每种颜色分别代表不同的放电周期，图5(b)是图5(a)的局部放大图. 红色代表1周期放电，黄色代表2周期放电，依次类推. 从双参数分岔图可以直观地观察系统放电周期的转迁规律. 由图5中的左下到右上，系统由1周期放电经过倍周期分岔进入混沌放电，之后又退化为4周期放电， 4周期放电又经过倍周期分岔转迁为混沌放电，继而又经过逆加周期分岔为3周期放电. 在达到3周期放电之前，系统一直呈现周期-混沌之间的转迁. 随着Iext与k1的增大，最终系统由加周期分岔呈现出稳定的2周期、3周期、4周期、5周期放电.

图4 关于参数Iext 峰峰间期分岔图Fig. 4 TheISI bifurcation diagram with respect to parameter Iext

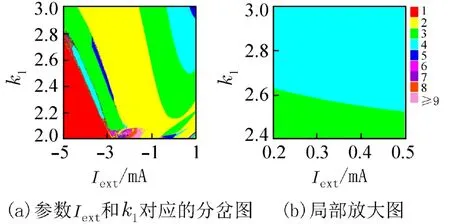
图5 双参数分岔图Fig. 5 Bifurcation diagram with two parameyers

当图5(a)中横坐标取Iext=0.4 mA时，从下到上的周期转迁过程如图2(a)的单参数分岔图所示. 同理当纵坐标k1=2.5 时，系统从左到右的周期转迁过程如图4(a)的单参数分岔图所示.

3 磁通耦合胰腺β细胞的同步研究

3.1 磁通耦合胰腺β细胞达到同步的条件神经元的同步行为是生物体突触之间能否正常传递信息的关键，它在生物界领域应用十分广泛，而神经元的电活动依赖于神经系统复杂的电生理状态[18]. 文献[19]认为在神经元中应考虑电磁感应的影响. 本文在此基础上，研究磁通耦合胰腺β细胞达到同步的条件. 通过磁场耦合的方式耦合的神经元称为磁通耦合神经元模型，该模型可表示为:

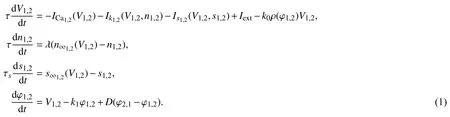
D(φ2-φ1)表示第1个神经元到第2个神经元的耦合项，D(φ1-φ2) 表示第2个神经元到第1个神经元的耦合项，这里采用磁流双向耦合. 首先在不加耦合项的情况下把系统简化为[20-21]：

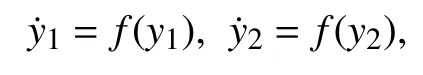
这里的y1=(V1,n1,s1,φ1),y2=(V2,n2,s2,φ2)，f:Rn→Rn是函数.

其次通过双向磁通耦合的方式得到耦合系统：

这里的W是耦合强度矩阵，则

当系统达到完全同步则相当于系统去除瞬态响应之后与V1-V2→0，n1-n2→0，s1-s2→0，φ1-φ2→0等价. 也即为 ‖y1-y2‖=0⇔‖E‖=0.

同步差满足的方程为：

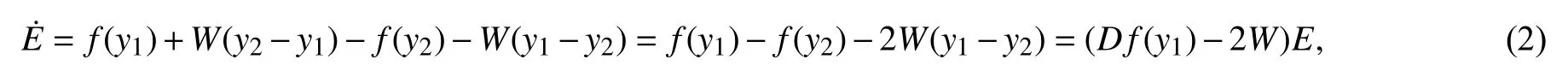
其中Df(y1)表示向量场f的Jacobi矩阵在变量y1处的取值[22]，此时磁通耦合胰腺β细胞的完全同步问题就转化为方程(2)零解的渐进稳定性问题.

由方程(1)得到：

现令：

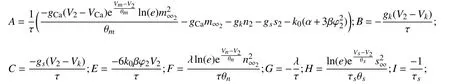
则此时

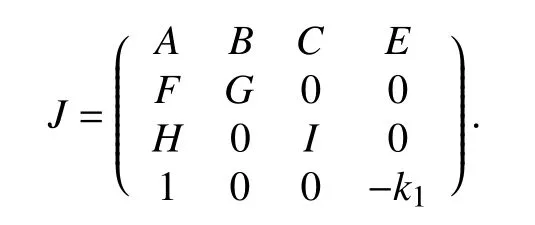
根据模式分解法[23]，则记J-2W的对角化矩阵为

则：

相似矩阵有相同的特征值，所以判断方程(2)零解是渐进稳定的只需要判断R的特征值的实部均为负. 现在假设系统已经达到完全同步的状态，则R是负定的，则满足如下关系式:

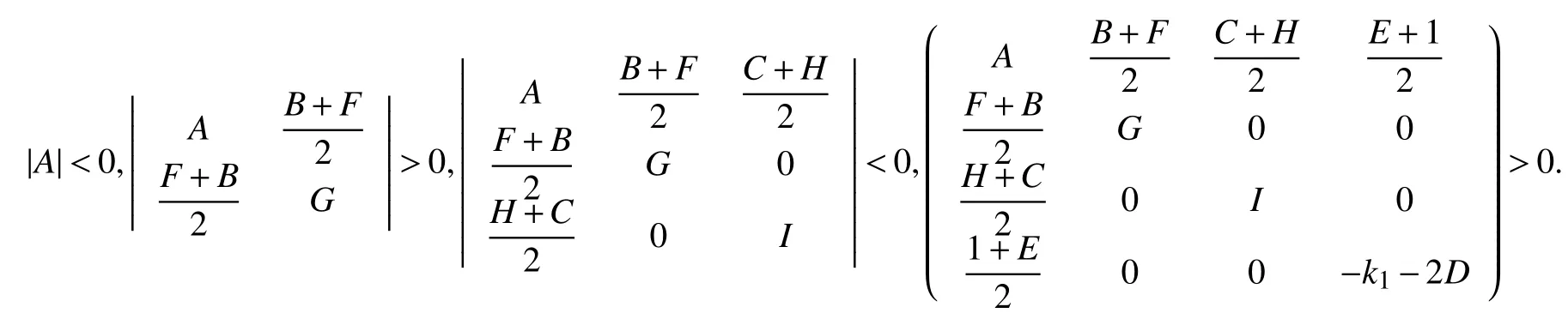
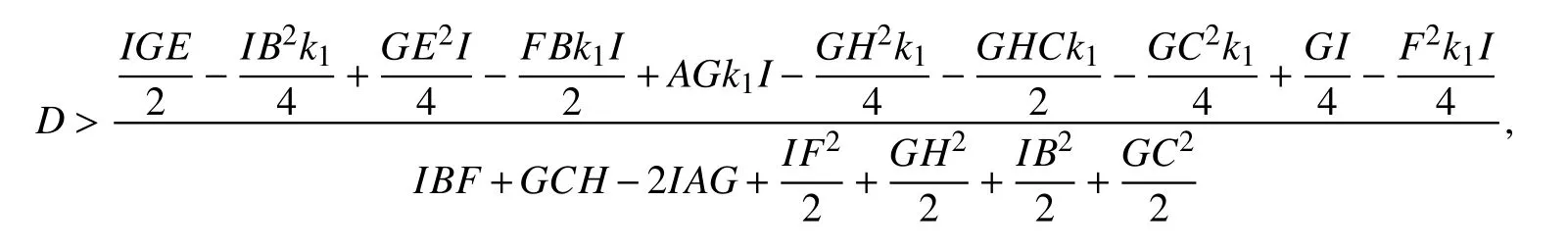
同步差

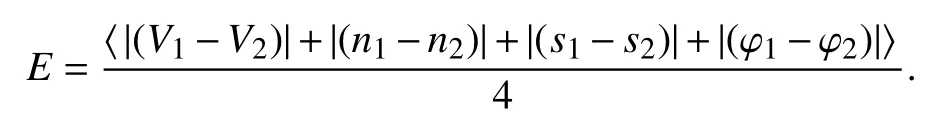
〈*〉表示平均，‖E‖=0，系统是达到完全同步的.

固定基准参数，耦合强度D变化时系统的膜电位，同步差随时间的变化如图6所示.

图6(a)，(d)，(g)是不同耦合强度下系统的时间历程图；图6(b)，(e)，(h)是不同耦合强度下系统V1和V2的相图；图6(c)，(f)，(i)是不同耦合强度下系统同步差图. 当D=0.01 时观察系统的时间历程图，图中黑色实线代表V1的时间序列，红色实线代表V2的时间序列；2条轨线差距一直保持一个不为0的定值. 从图6(c)中也可以看到虽然同步差是1条直线，但不是E=0 的直线，所以此时系统并没有达到完全同步，随着耦合强度的增大，当D=0.045 时从图6(d)中可以看出，系统还是没有达到同步，但是二者轨线之间的差距已经更加接近了，从图6(f)同步差图中可以看出，随着时间的变化，E的值在减小，并不是一条固定的直线.图6(g)～(i)此时耦合强度为0.1时，可以看到时间历程图完全重合，V1和V2的相图是1条斜率为1的直线，同步差图为E=0 的直线，表明在上述耦合强度下此磁通耦合胰腺β细胞系统达到了完全同步状态.

图7为同步差随耦合强度D的变化图，从图中可以看出耦合强度为0.1时，系统达到了完全同步.

由同步差的性质知当 ‖E‖=0 时，系统达到完全同步状态. 完全同步也就为峰簇均达到同步，是一种多尺度现象. 刚开始时D=0 两个系统之间没有通过磁通耦合建立联系为2个独立的个体，因此系统处于不同步的状态；当D=0.032 4时，系统发生了簇同步说明神经元簇的同步比峰的同步更容易完成；随着D的逐渐增加，当D=0.075时系统已经达到完全同步，在D∈(0,0.075) 此时增大耦合强度对于系统达到完全同步具有促进作用，但是当D=0.225时，E≠0，则系统不再处于完全同步状态，此时增大耦合强度，反而破坏了系统的同步.

为了探究外部电刺激Iext与反馈增益k1二者同时变化对耦合神经元系统同步的影响，利用同步差原理和离散耦合强度，得到不同耦合强度下双参数同步差的云图，如图8所示.

图8中色条代表一定耦合强度下的系统同步差值，为了从图中精确表示系统达到完全同步的范围，此时把同步差的范围改为0～0.01，图8中红色区域表示系统达到完全同步态. 非红色区域为不完全同步态.从图8中观察到系统要达到同步的状态随着Iext的值增加，而对应的k1的值呈递减趋势. 并且随着耦合强度的增加，系统的同步区域逐渐增大，表明在弱耦合强度下，耦合强度的增大对系统的同步具有促进作用.

将外部电刺激Iext、反馈增益k1分别于耦合强度D进行组合，对耦合神经元系统同步进行双参数分析, 研究磁通耦合β细胞在两个变量时作用下系统的同步状态.

图9(a)是固定k1，改变Iext和D的双参数同步图，图9(b)是固定Iext，改变k1与D的双参数同步图.图9中深蓝色区域是系统达到同步的区域，而浅蓝色是系统没有达到同步的区域. 观察图9(a)和图9(b)可以看出，当系统处于弱耦合强度时，不论参数Iext与k1如何变化，系统都无法达到同步状态，但随着耦合强度的增加，系统会出现同步的可能. 也进一步说明了在一定的弱耦合强度范围内，耦合强度D的增大对于系统的同步具有促进作用. 当Iext的值小于0.3时，随着D的增大系统也很难达到同步状态，此时耦合强度对于系统的同步没有促进作用. 进一步验证，图9(b)中k1∈[2.55,3] 时，无论耦合强度如何变化，系统都达不到同步的状态. 说明此时耦合强度不是系统达到同步的主要影响因素. 当Iext∈[0.3,0.5]，D∈[0.1,0.3] 之间，此时系统处于同步状态的范围大大增加. 但随着D增加到0.34时，无论Iext如何变化，系统始终达不到同步状态，此时外部电刺激Iext不是系统达到同步的主要影响因素. 对于图9(b)在选取的范围内只有k1∈[2.46,2.55] 之间系统才具有同步的可能.当D增加到0.359时，无论k1如何变化，系统始终达不到同步状态，此时k1不是系统达到同步的主要影响因素.

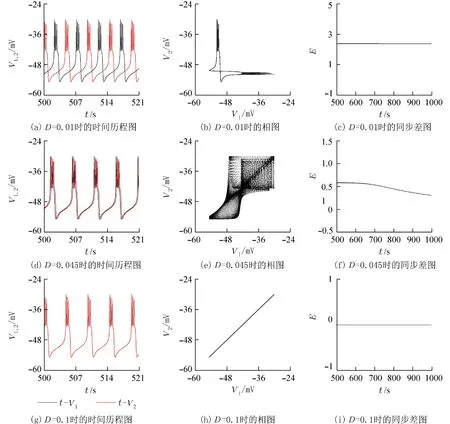
图6 系统(1)在不同耦合强度下的放电及同步分析Fig. 6 Discharge and synchronization analysis of system (1) under different coupling strength

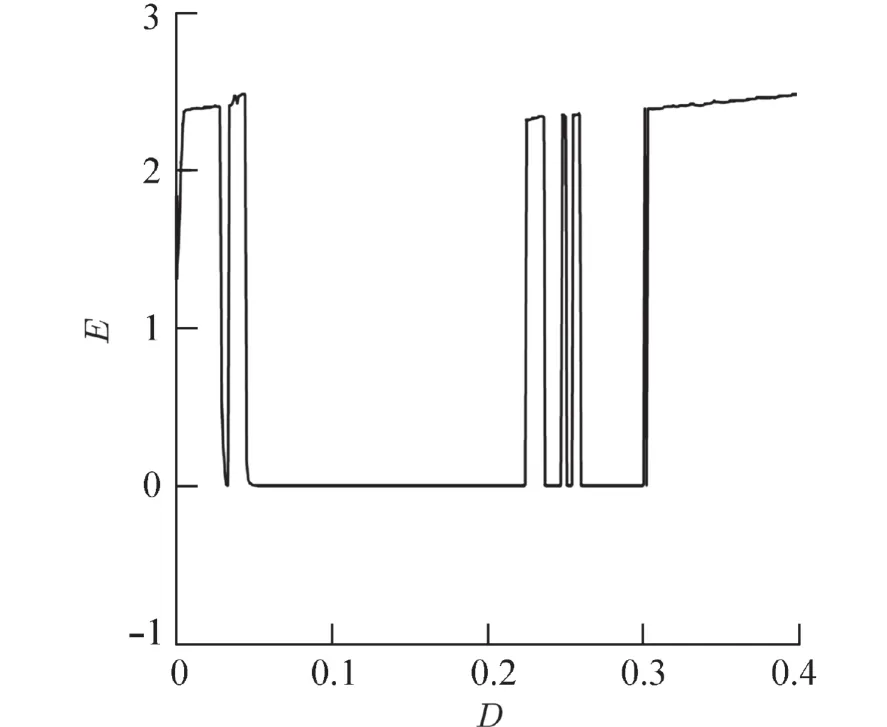
图7 同步差随耦合强度的变化图Fig. 7 Variation of synchronization difference with coupling strength

图9 不同参数与D对应的同步图Fig. 9 Synchronous diagram corresponding to different Parameters and D

4 结论

通过对胰腺β细胞引入磁通量的研究发现，在外界电刺激和磁通量作用下，神经元呈现丰富的动力学行为. 首先，分析单个磁流作用下参数k1和外部电刺激Iext对神经元放电模式的影响. 从分岔图看出参数的改变使系统在加周期分岔，逆加周期分岔与倍周期分岔之间相互转换，出现静息态、峰放电、簇放电等多种放电模式，且在给定的参数范围内，Iext的改变更加丰富了系统的放电模式. 对胰腺β细胞引入磁通量，研究发现在外界电刺激和磁通量作用下，神经元呈现丰富的动力学行为. 其次，对磁通耦合的胰腺β细胞的同步进行研究，利用同步差原理，采用假设法，推导得到系统达到完全同步状态的条件. 最后，进行双参数分析，离散耦合强度. 研究发现参数k1和外部电刺激Iext同时变化时，系统处于弱耦合强度时神经元系统对耦合强度非常敏感，随着耦合强度的增大，系统将逐渐趋于同步的状态，说明此时增大耦合强度对系统的同步有促进的作用. 但是当系统的耦合强度由弱变强时，分析Iext与D，k1与D的同步图，发现在一定的范围内的耦合强度不仅不能促进系统达到同步，而且也不是系统达到同步的主要影响因素. 本文对引入忆阻器的胰腺β细胞放电及同步特性的研究，为进一步探索电磁感应对神经元的影响提供参考.