基于自适应混沌遗传算法的影响力最大化研究

张 萌，李维华

(云南大学 信息学院，云南 昆明 650500)

随着Facebook、Instagram和微博的不断发展，社交网络逐渐成为信息传播、商业宣传的绝佳平台，一些研究者通过用户的行为模式进行数据分析，挖掘社交网络作为信息扩散平台的潜力. 影响力最大化问题作为社交数据分析下的新兴领域，利用最少的资源获得最大影响，在病毒营销、信息扩散、舆论监测和医疗保健中发挥着重要作用.

社交网络影响最大化问题是如何选取K个初始节点进行传播，从而最大程度地影响整个网络的问题[1]. 2002年，Richardson等[2]首先提出影响力最大化问题并将其定义为一个算法问题. 随后Kempe等[3]证明了在特定传播模型下的影响力最大化问题是NP难问题，利用离散优化思想发现K个影响增益最大的节点使得最终的影响范围最大，并提出贪心爬山近似算法. 针对传统贪心算法耗时过多的缺点，Leskovec等[4]利用函数的子模性，提出了CELF(Cost-Effctive Lazy Forward)优化算法, 大大提高时间效率的同时也达到了和传统贪心算法一样的影响范围. Ding等[5]引入一个现实独立级联模型(Realistic Independent Cascade，RIC)，基于该模型提出了3种新的传播算法R-greedy，Mgreedy和D-greedy. 这些改进的贪心算法可以在简单网络上显示出良好的性能，但每次迭代都需要进行上万次的蒙特卡洛（Monte Carlo，MC）模拟才能得到近似解，在中大规模的复杂网络中计算量很大. 为了降低影响最大化问题的时间开销，高效的智能算法为解决影响力最大化的问题开辟了新方向. Jiang等[6]提出了一种预期扩散值度量(Expect Diffusion Value，EDV)近似估计潜在节点的影响力，结合模拟退火算法(Simulated Annealing，SA)可识别有影响力的节点. 该算法比贪心算法在时间花费上节约了近3个数量级. Cui等[7]提出了一种节点度递减搜索策略并基于差分进化与遗传算法提出影响力最大化算法(Degree-Descending Search Evolution，DDSE). 钱付兰等[8]利用免疫选择优化遗传算法，再根据局部概率解评估影响力. 实验表明遗传算法在影响力最大化的求解中比模拟退火算法在性能和时间上更具有优越性. Gong等[9]等将改进的粒子群算法与二跳局部影响估计器相结合提出DPSO (Discrete Paticle Swarm Optimization)算法. Liu等[10]通过搜索空间划分机制来增强搜索，提出了基于模拟退火的高效算法SASP(Simulated Annealing with Search Partition). Sankar等[11]通过探索蜂群的摇摆舞行为，提出了一种用于最大化影响力的蜂算法，并在Twitter数据集上验证了该算法的性能. 此外，Zhang等[12]根据信息传播的概率性，提出精确概率解影响力估计，利用增量式搜索解决影响力最大化问题. 以上方法虽然大大提高了算法的运行效率，但除了SASP算法，其余算法只是在简单网络中验证了算法性能，没有运用到中大型网络中，而且一些智能算法存在参数设置困难，使得节点影响估计不足导致算法性能明显下降. 如何能在合理的时间消耗内很好地平衡求解精度，使得算法在不同规模的网络中仍然能保持稳定搜索，是影响力最大化问题面临的一个挑战.

本文采用一阶容斥激活集（the First-order Inclusion-Exclusion Activation set，FIEA）作为适应度函数评估节点集的预期影响，利用Logistic混沌序列的均匀搜索能力和自适应变异稳定而高效的局部寻优特点，提出一种自适应混沌遗传算法（Self-Adapting Chaos Genetic Algorithm，SACGA）迭代出最优种子集，然后再将该种子集经过特定的模型传播后得到最终的影响范围.

1 影响力最大化问题

1.1 问题定义在求解影响力最大化问题时一般将网络定义为图G=(V,E)，其中V代表节点，E代表边即节点间的联系. 从网络中选出K(1≤K≤|V|)个不重复节点组合成一个种子集S，让S在特定的模型下进行影响传播，得到的影响扩散范围δ(S)要达到最大，S*为最佳种子集. 影响力最大化问题的形式化定义为

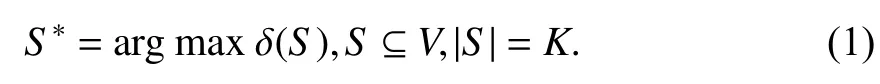
1.2 影响力传播模型在影响力最大化问题中，影响传播模型通常使用独立级联（Independent Cascade，IC）模型和线性阈值（Linear Threshold，LT）模型. 这里详细介绍本文使用的IC模型.

IC模型是一种概率模型，当节点a被激活后，以一定概率去尝试激活它的邻居节点b，并且a对b的激活过程独立，不受任何节点影响. 该模型的传播过程如下：

（1）在某个时刻给定一个种子集S（S中的节点均为活跃状态，S以外的节点均为非活跃状态），在该时刻节点a被激活后，它就获得了一次以概率P去激活节点b的机会.

（2）若节点b有多个邻居均处于活跃状态，这些邻居会以任意顺序去尝试激活节点b. 如果节点b被成功激活，那么在下一时刻，节点b的状态变为活跃，可以去激活其他未被激活的节点.

（3）重复过程（1）和（2），直到网络中没有可以激活的节点. 当整个过程结束时，得到的是网络中被激活的节点数.

1.3 预期影响评估Zhang等[12]基于IC模型，从概率角度出发提出精确概率解评估节点影响，同时证明了该方法遵循容斥原理（Principle of Inclusion-Exclusion, IE）. 利用容斥原理能够在较少的时间成本内在网络中找到具有影响潜力的种子集. 在复杂网络中，给定一个节点v所有处于活跃状态的入度邻居节点Iv={w1,w2,...,wk} 和边概率Pwkv，利用容斥原理计算节点v的被激活概率为

简化后可得

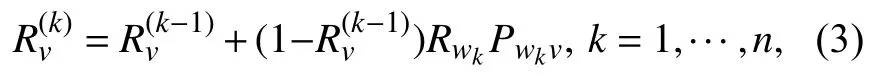
其中 ，k为v的活跃入度邻居数，Rv(0≤Rv≤1) 是为v的被激活概率，表示节点v被激活的程度.

具体实例如图1所示，有一个种子集S={2,3},种子集中节点均为活跃状态，其余节点均不活跃.节点4有两个活跃入度邻居，由式（3）计算可得节点4的被激活概率

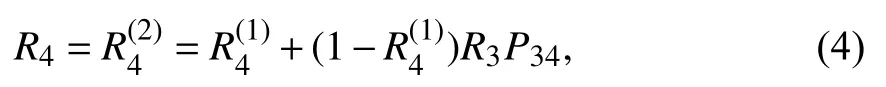
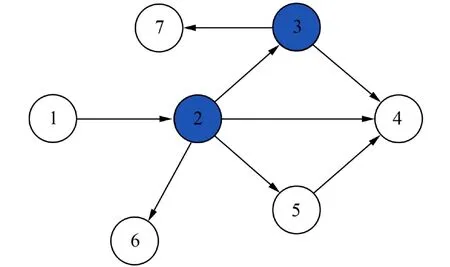
图1 一个小型网络Fig. 1 A simple network

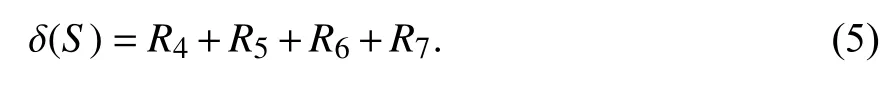
2 自适应混沌遗传算法

利用遗传算法求解影响力最大化问题的可行性已被验证[13-14]. 遗传算法擅长在全局范围内搜索，使得算法不陷入局部最优且收敛快. 但遗传算法的局部搜索能力差，特别是进化后期搜索能力的降低容易导致早熟收敛. 针对这些不足，提出一种自适应混沌遗传算法.

2.1 编码方式选择实数编码方式. 任意一个种子集S={s1,s2,···,sK}表示由K个不重复节点组成的集合，S中的每个元素表示网络中的节点编号，每个编号都是唯一的.

2.2 适应度函数适应度函数在遗传算法中表示个体适应环境的能力，可以用此衡量种群中个体的优劣. 适应度高的个体有更大的概率在种群中生存下去，而适应度低的个体则会在进化过程中被逐渐淘汰. 在提出的算法中，适应度用于在迭代过程中评估种子集的预期影响. 在Zhang等[12]研究工作的启发下，给定G=(V,E) 和任意种子集S，S中的节点均为活跃状态，某个节点的被激活概率为Rv，利用容斥激活集（Inclusion-Exclusion Activation set，IEA）可计算种子集的预期影响

其中，M表示在集合中而不在S的节点，表示S中节点的n阶邻域内的所有非激活邻居节点. 当n取值为 ∞ 时，得到的是种子集S的全局网络预期影响评估，但根据影响力的传播动力学研究显示，由于影响衰减，最近邻域范围内的影响评估往往是最可靠的[15]. 因此，本文采用FIEA作为适应度函数评估种子集的预期影响

2.3 产生初始种群实际上在真实的网络中存在大量影响力极低的节点，这些节点并不能作为影响候选节点. 为了提高搜索效率，首先将单个节点看作一个种子集，利用适应度函数计算图G中每个节点的预期影响σ1(vi)，并将这些节点按预期影响的大小进行降序排列 σ1(v1)＞σ1(v2)＞···＞σ1(v|V|)，从前L个节点中随机产生初始种群，同时选择前K个节点构造关键节点集Q.

2.4 混沌顺序交叉混沌的基本思想是根据一定规则让未知变量从原有混沌空间变换到求解空间，利用混沌本身的随机性、遍历性和规律性等特点对解空间进行混沌搜索，从而求得全局最优解[16].由一个确定性方程得到，但具有随机性的活动状态称为混沌. 当前的混沌优化大多采用Logistic映射混沌序列，定义如下：

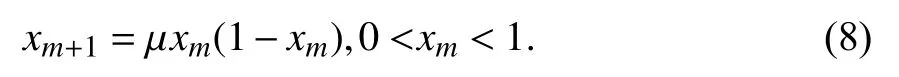
其中，μ 为控制参数，当μ∈(3.5 699 456,4] 时系统进入混沌状态；当μ=4 时，Logistic映射为满映射，整个系统处于完全混沌状态，生成的混沌序列具有良好的随机性. 因此在本文中 μ 的取值为4，初始xm为0到1之间的随机数.

采用混沌顺序交叉，既能均匀地增加种群的多样性，也避免了个体基因位上的冲突. 选择种群内的个体进行配对，两两组成父代，然后具体交叉过程如图2所示.

步骤1从种群中依次选取父代个体X1和X2，随机产生混沌初始值，利用式（8）产生一个混沌值，把该混沌值作为混沌序列的初值生成另一个混沌值，再将这两个混沌值分别与K-2 相乘得到两个正整数g和h(0≤g≤h≤K-1) 作为父代截取基因的起始位置和终止位置，截取出的基因称作交叉基因段.

步骤2生成一对个体X1′和X2′，并保证个体中被选中的基因位置与父代X1和X2的相同.

步骤3找出父代X1中与X2′交叉基因段中不相同的基因，按顺序放入X2′的空位中，生成新子代Y1.X2与X1′重复同样的操作得到另一个新子代Y2，交叉过程结束.

2.5 自适应混沌变异自适应混沌变异的思想是指当种群中个体的适应度差距逐渐缩小并趋于收敛时，需要增大变异概率以破坏当前种群的稳定性. 在变异时，同样利用式（8）迭代生成两个混沌值xm+1和xm+2，再与K-2相乘得到两个正整数a和b(1≤a≤b≤K)，表示个体基因位. 从关键节点集Q中随机选取一个节点替换基因位上的基因，生成新的子代，跳出当前最优，避免算法早熟. 而当种群中个体的适应度差距较大时，应降低变异概率，使算法趋于收敛.{S1,S2,···,SN} 表示一个种群，N为种群大小，S j表示种群中当前待获取变异概率的个体，该个体变异概率为

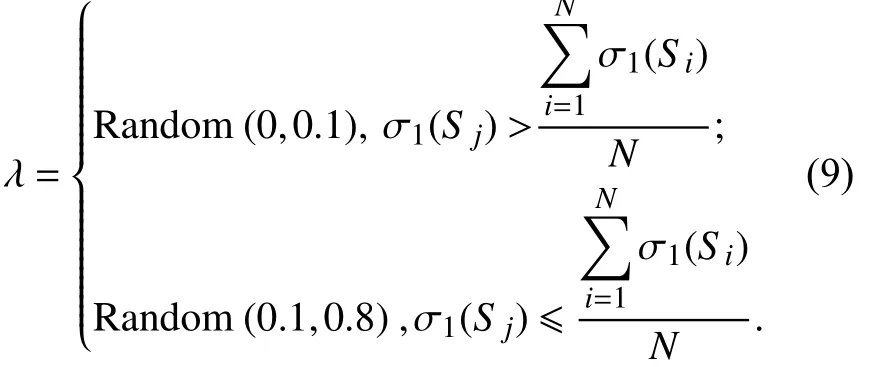
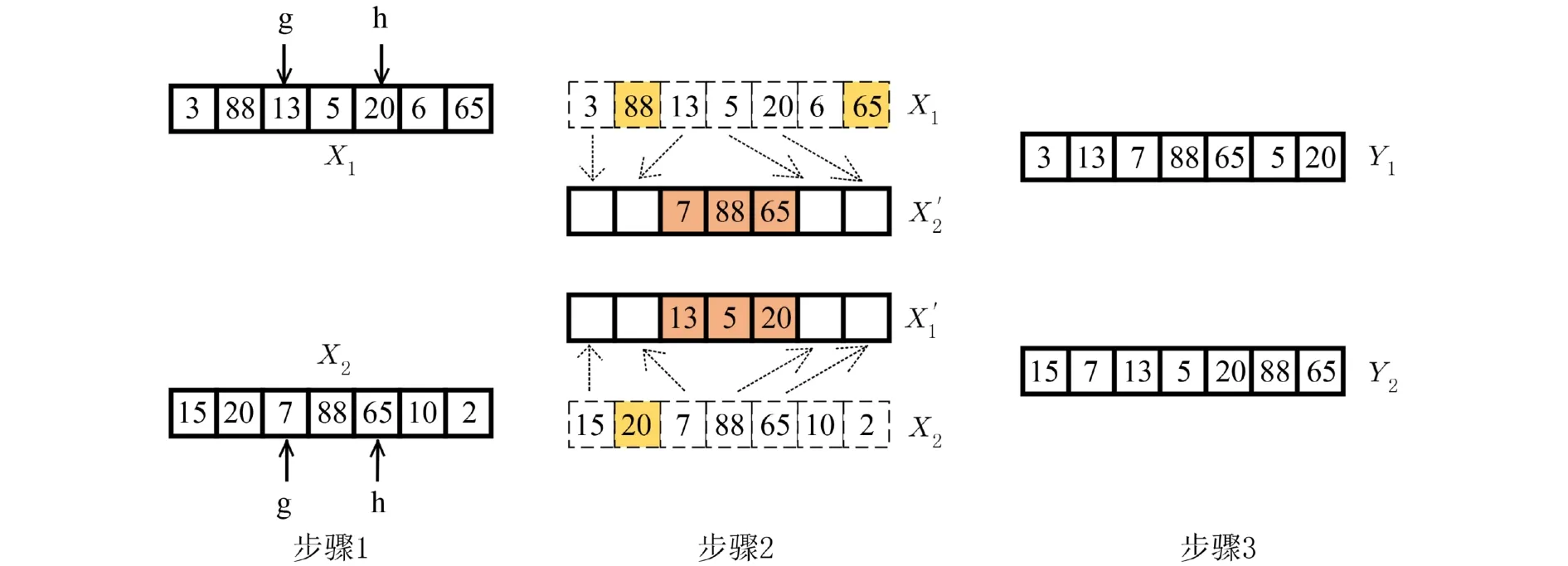
图2 顺序交叉过程Fig. 2 The process of sequential crossover

算法1描述计算节点集的预期影响函数σ1(S)

输入：G=(V,E)，边概率P，种子集S.

输出：种子集S的预期影响.

步骤1种子集中节点的激活概率初始化为1，网络中其余节点的激活概率初始化为0.

步骤2找出种子集S中节点的n个一阶邻居节点.

步骤3利用式（3）计算得到每个邻居节点的激活概率.

步骤4由式（7）得到种子集S的预期影响.

算法2描述自适应混沌遗传算法SACGA

输入：G=(V,E)，边概率P，种群大小N，种子集大小K，交叉概率 γ，迭代次数Imax.

输出：最佳种子集Sbest.

步骤1利用适应度函数 σ1计算G中所有节点的影响分数. 从前L个节点中随机生成N个大小为K的个体组成初始种群S={S1,S2,···,SN}，同时选取前K个节点构造关键节点集Q.

步骤2从初始种群中选出初始最优解Sbest.

步骤3开始进行种群迭代.

步骤4依次从当前种群中选取两个个体作为父代. 如果当前父代的 γ 满足交叉条件就随机产生混沌初始值xm，由式（8）计算得到两个混沌随机数xm+1和xm+2，将两个随机数分别与（K-2）相乘得到g和h，根据g、h进行基因位顺序交叉. 如果不满足交叉条件，则直接进入新种群.

步骤5得到交叉后的新种群N′.

步骤6在新种群N′中的个体j. 根据式（9）产生变异概率 λ，如果 λ 满足变异条件，随机产生初始混沌值xm，由式（8）迭代生成xm+1和xm+2，将两个随机数分别与（K-2）相乘得到a和b. 从Q中随机选择节点与a和b上的基因进行交换，如果λ不满足变异条件，则进入下一阶段.

步骤7如果 σ1(S j)＞σ1(Sbest)Sbest=S j.

步骤8得到变异后的种群.

步骤9更新种群，如果迭代次数小于Imax，跳至步骤3，否则跳至下一阶段.

步骤10迭代完成后输出最佳种子集Sbest.

D(-)为节点平均度，Imax为最大迭代次数，K为种子集大小. 算法1的时间复杂度为O(nKD(-)).算法2产生初始种群的时间复杂度为O(nKD(-))+O(NnKD(-))，迭代过程的时间复杂度为2O(NKImax)+O(NImax)+O(NnKD(-)Imax). 因此，最坏情况下SACGA算法的时间复杂度为O(NnKD(-)Imax).

3 实验与结果分析

本文利用4个真实的网络数据集（数据来源：http://snap.stanford.edu/data）进行实验结果的对比和分析，验证所提一阶容斥激活集FIEA和自适应混沌遗传算法SACGA的有效性.

3.1 数据集网络数据集如表1所示.

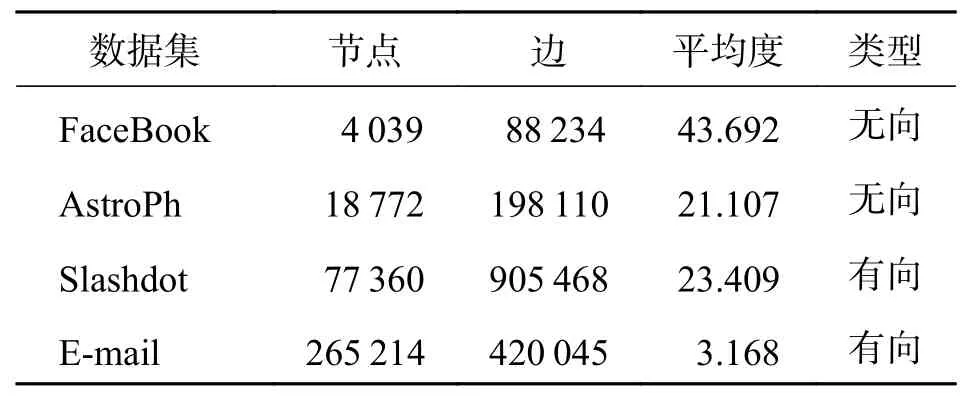
表1 社交网络数据集Tab. 1 The data sets of social network

3.2 对比算法与实验设置为了验证SACGA的有效性，本文选取4个具有代表性的算法与SACGA进行对比，边概率P统一设置为0.01. 其中SAEDV算法的参数为初始温度Ti=500 000，结束温度Tf=100 000， 降温系数 ΔT=2 000 和外循环q=10；DDSE算法参数为种群大小N=10，种群多样性d=0.6 ，交叉概率 γ=0.4 ，变异概率 λ=0.1，迭代次数为200次；GA算法的参数设置为种群大小N=10， 交叉概率 γ=0.4 ，变异概率 λ=0.1，迭代次数180次；SACGA-N是在SACGA下利用n=∞ 时的IEA函数寻找种子集的算法，其参数设置与SACGA相同. 上述算法的结果均由运行10次的平均结果得出. 所有代码使用Python3编写，实验在Windows（Intel Corei5.2.3 GHz,8 GB内存）下进行.

关键节点集Q的设置使得算法能够跳出当前最优，以便寻得更优秀的个体，从而加速算法收敛.如图3所示，在4个数据集中，当Q取值为K时，影响范围达到最大，随着Q取值不断增大，影响范围呈下降趋势，在FaceBook和E-mail数据集上尤为明显. 因此，本文关键节点集Q的取值为K. 此外，为了提高时间效率，将种群大小设置为10，SACGA算法的具体参数设置如表2所示.

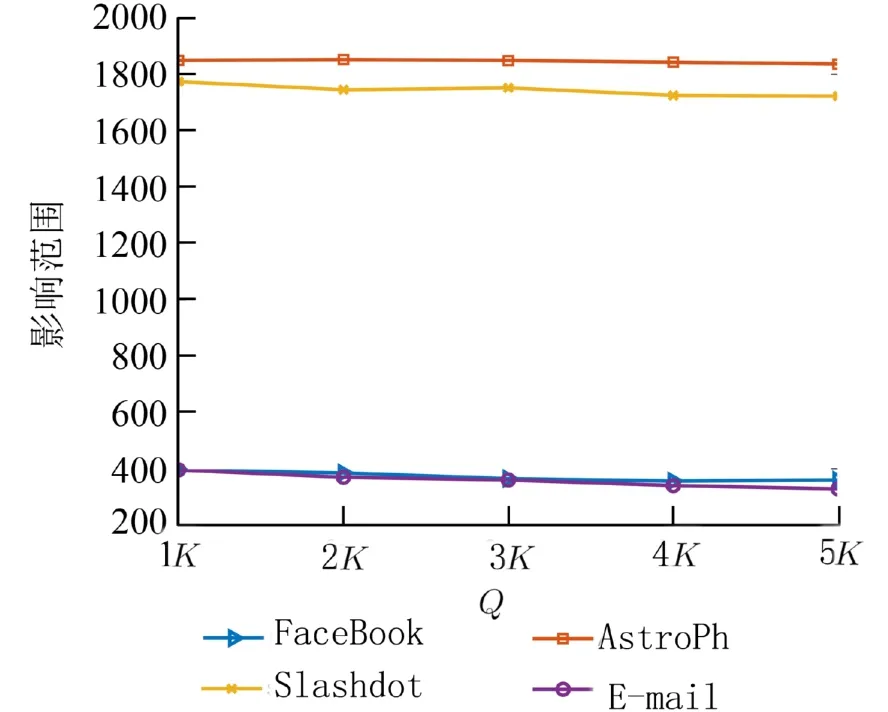
图3 关键节点集 Q 取值与影响范围的变化Fig. 3 The variations of influence spread with differet values of Q

表2 SACGA算法参数设置Tab. 2 The parameter setting of SACGA

3.3 实验结果与分析评价影响力最大化算法的性能通常使用影响传播范围和运行时间这两个常规指标. 影响传播范围指利用影响力最大化算法寻找到的种子集在特定传播模型下的影响范围大小；运行时间即算法寻找到最优种子集所花费的时间.

3.3.1 预期影响评估方法对比 本文利用FIEA评估种子集的预期影响以便选出最优种子集. 为了验证该方法的有效性，选取K为50的种子集在FIEA和IEA上进行影响范围和运行时间的对比. 如表3所示，除了在FaceBook数据集上利用IEA进行评估选出的种子集在影响范围上比FIEA多了0.34%，在其它3个数据集上，利用FIEA评估出的种子集产生的影响范围均比IEA分别扩大了0.24%、0.069%和7.22%. 说明利用FIEA评估种子集的预期影响是一种可靠的方法. 同时本文给出了利用FIEA和IEA计算一个种子集预期影响的运行时间对比，如表4所示，在4个数据集上FIEA只需要不到1 s的时间就能计算出大小为50的种子集的预期影响，而IEA则需要几十秒最长103.671 s才能计算出一个种子集的预期影响，相比起IEA，FIEA节省了很多时间，是提高算法效率的一个有效途径. 因此，利用FIEA评估种子集的预期影响是合理且高效的.

表3 FIEA和IEA的影响范围对比Tab. 3 Comparison of influence spread about FIEA and IEA

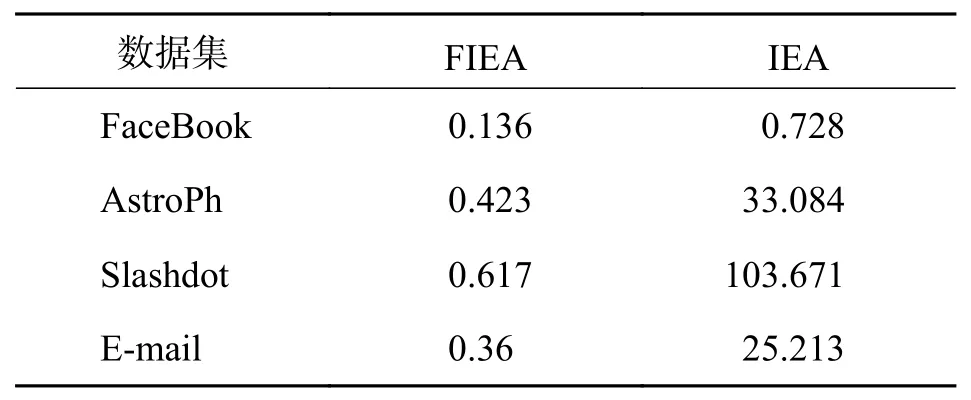
表4 FIEA和IEA的运行时间对比(单位：s)Tab. 4 Comparison of running time about FIEA and IEA(Unit: s)

3.3.2 影响范围对比 本文的影响范围是指种子集经过IC模型传播后得到的种子集在一个网络中激活的节点数目，激活的节点数越多，影响范围越大，算法性能也越好. 由于传播过程中的随机性，将各算法选出的最优种子集以固定传播概率P=0.01在IC模型下进行10 000次的蒙特卡洛模拟，并在图4中给出了5个算法在不同种子集大小下的平均影响范围.

如图4所示，整体来看，SACGA在4个数据集中的表现最好，性能也最稳定，而GA的表现最差. 在FaceBook和E-mail这两个数据集中SACGA明显领先其它算法，当K=50 时，在E-mail数据集中SACGA的影响范围比DDSE、SAEDV、GA和SACGA-N分别扩大了22.76%，5.06%，280.09%和7.79%. 需要注意的是，根据全局预期影响选择种子集的算法SACGA-N的性能并没有想象中的好，虽然在FaceBook和Slashdot数据集中，SACGA-N的性能仅次于SACGA，但在AstroPh数据集上，当种子集大小为20和30时，SACGA-N的影响范围比SAEVD和DDSE分别低了0.67%和0.3%，0.5%和0.26%. 此外，同样在FaceBook和Slashdot数据集中，当K＜30 时，SAEDV的性能落后于DDSE，在FaceBook数据集中尤为明显，但随着K＞30，SAEDV的性能逐渐优于DDSE，并且在AstroPh和E-mail数据集上，SAEDV的性能明显优于DDSE. 在4个数据集中可以看到，DDSE后期搜索能力明显不足，说明基于度的方法在搜索过程中还是存在一定的局限性，特别是在稀疏网络中. GA算法性能相比其它算法性能差的原因可能是算法没有跳出全局最优导致搜索能力不足，不能寻找到优秀的种子集. 综上所述，相比起其它算法，SACGA在搜索时能跳出当前最优，并且表现良好，性能也较稳定.

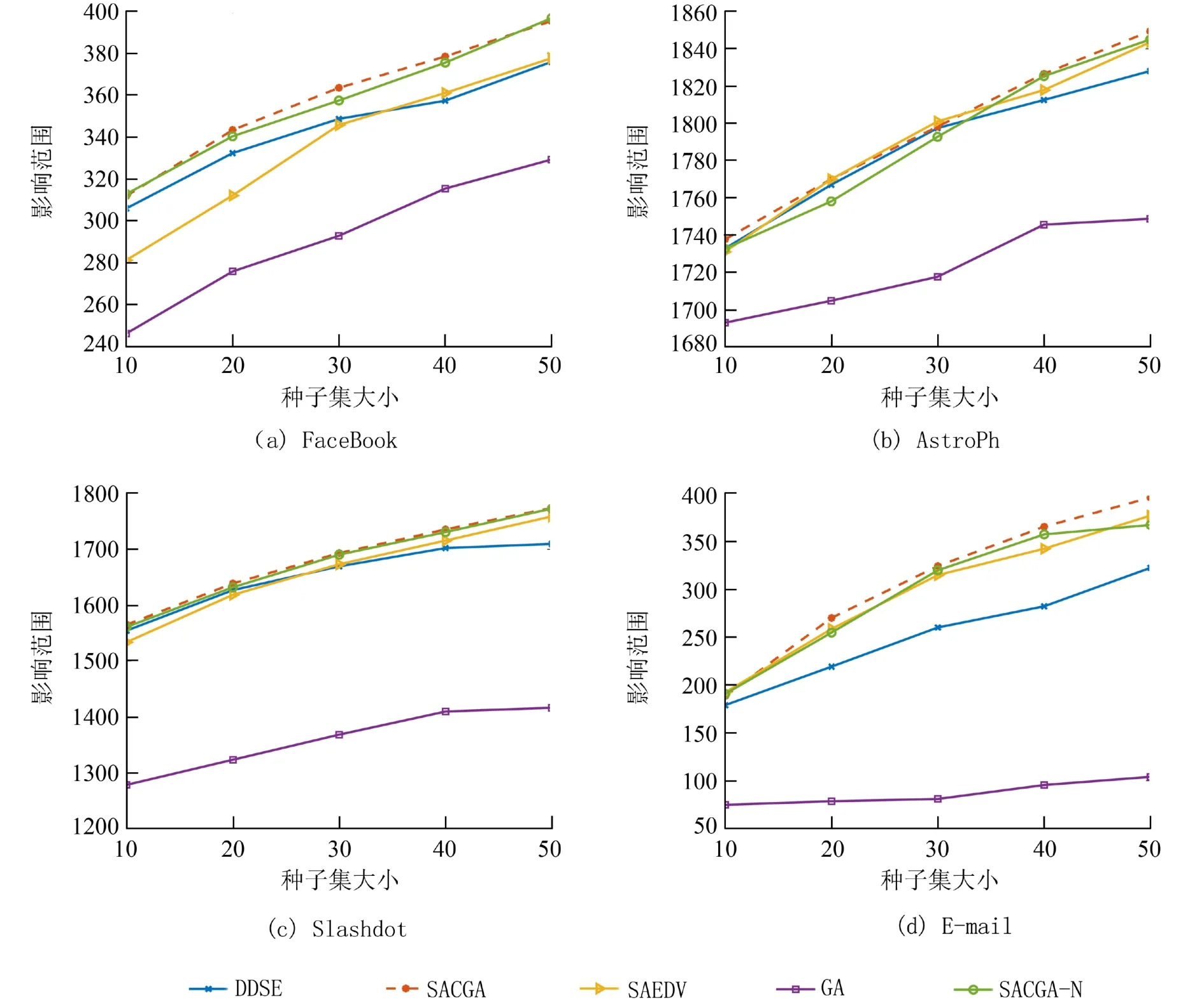
图4 算法在不同数据集上的影响范围Fig. 4 Influence spread with different data sets

3.3.3 运行时间对比 为了验证算法的高效性，本文给出5个算法在4个数据集中寻找到50个最佳种子节点的运行时间对比，如图5所示，GA的时间效率最高，但GA性能最差. DDSE的运行时间也较短，但算法性能也不稳定. 而SAEDV由于要进行数万次的迭代，所以网络规模越大，耗时也越多. 虽然SACGA的运行时间比GA和DDSE的多，但其产生的影响范围均比这两个算法大，可以弥补在时间上的不足. 相比起SAEDV，SACGA在4个数据集中的时间效率分别提高了52.01%，49.75%，55.88%和50.16%，节省了大量时间成本.而SACGA-N要对种子集中的每一个节点进行全局预期影响估计，所以非常耗时，在规模较小的FaceBook数据集中找到K=50 的种子集都需要5 433.014 673 s，高额的时间成本在数据量较大的网络中并不能成为一个合理的解决方案. 因此，实验结果表明，本文提出的SACGA能在影响范围和时间成本上有较好的平衡.

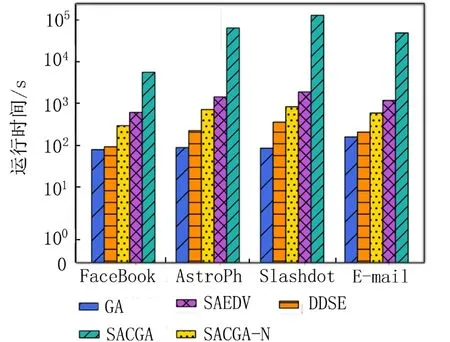
图5 不同数据集上的算法运行时间对比Fig. 5 Comparison of algorithms’ running time on different data sets

4 结束语

本文利用一阶容斥激活集作为适应度函数评估种子集的预期影响，提出一种自适应混沌遗传算法SACGA. 通过单个节点的影响力构造关键节点集，利用Logistic混沌序列均匀搜索和自适应变异来增强算法的局部寻优能力，加快收敛. 在4个真实数据集上的实验表明，SACGA在影响范围和运行时间两个指标上都有良好表现，验证了该算法的稳定性和高效性. 现有智能算法求解影响力最大化问题的方法还有很大的改进空间，如何合理设置初始种群和更好地改进算法设计，使得算法更加高效，也是需要进一步探究的问题.