隧道爆破振动信号混沌分形特征研究

付晓强，俞 缙，戴良玉，张会芝，黄凌君，杨 悦

(1.三明学院建筑工程学院，福建 三明365004；2.华侨大学福建省隧道与城市地下空间工程技术研究中心，福建 厦门 361021；3.三明科飞产气新材料股份有限公司，福建 三明 365500)

爆破信号具有典型的非平稳随机特性，识别和量化爆破信号中所包含的特征信息，是土木工程、岩土工程等领域关注的热点[1-2]。目前常用的非线性特征提取方法主要包括小波变换、希尔伯特-黄变换和神经网络等。小波方法中，小波基的选取对分析结果影响极大，其通常需根据信号的直观特点进行经验性选取，具有很大的盲目性；希尔伯特-黄变换克服了小波方法的小波基选取难题，但其算法存在的“端点效应”极易使信号内部受到不同程度的污染；而神经网络需要大量的数据对网络模型进行训练，且模型建立较为困难，工程实践对分析人员的理论水平要求较高。而近年来流行的混沌理论揭示了确定系统所可能产生的随机结果，可准确提取出非线性信号中包含的看似混乱却遵循特定规则的有序特征。

自Yan[3]提出频率切片小波变换(Frequency Slice Wavelet Transform，FSWT)分析方法以来，其优良的时频特性提取和解读能力得到信号分析领域广泛认可。其中，马朝永等[4]采用FSWT方法并结合谱负熵对轴承故障信号进行了分析，准确辨识出复杂故障信号中包含的周期性冲击循环平稳信息。蔡剑华等[5]提出了基于频率切片小波变换时频分析的大地电磁信号去噪方法，对仿真信号和实测信号的分析验证了结果的准确度。杨仁树等[6]采用EMD和FSWT组合方法对隧道爆破振动信号进行分析，提取到信号更为精细化的时-频-能量特征信息。

对非线性信号建立物理模型进行分析是复杂的，混沌理论为非线性信号特征的提取提供了十分有效的手段。马飞等[7]对生物物种时间序列进行分析，改进了物种发生预测模型，掌握了其发生演变规律。孙迪等[8]应用混沌理论研究了摩擦副磨合过程中摩擦振动混沌吸引子的演化规律，根据摩擦振动吸引子在相空间的体积变化表征了磨合不同阶段的振动特征。 由于爆炸过程的瞬态性以及振动波传播过程的复杂性，使得爆破信号的非线性特征对其传播机理的认识极为重要，现阶段针对隧道爆破信号的非线性混沌特征研究的文献还未见报道。

爆破振动信号特征提取是爆破振动危害控制的前提。为了研究爆破信号混沌非线性特征与信号振幅、主频及持续时间等参量的相关性，本文对隧道爆破振动信号进行频率切片小波变换实现不同频带子信号重构，从非线性角度得到了信号在不同频带内动态变化的混沌特征对爆破信号幅值的确定、主频有效判别及预测，爆破振动奇异监测信号的剔除等均具有非常积极的现实意义。

1 算法基本原理

1.1 FSWT算法

令L2(R)为有限向量空间(R为实数集合)，对于任意信号f(t)∈L2(R),频率切片小波的变换以母小波函数p(t)的傅里叶变换存在为前提[9]，即：

(1)

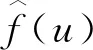
利用Parseval方程对式(1)进行变换，得到其时域表示形式为

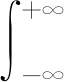
(2)

FSWT逆变换可实现信号重构，假定信号FSWT变换为W(t,ω,λ,σ)，任意选取时间区间(t1，t2)和频率区间(ω1，ω2)，可以得到该时频空间上的信号分量[10]：

(3)

1.2 吸引子相空间重构

本文采用C-C法重构相空间，具体过程[11-12]如下：

对任意一维时间序列x={xi,i=1,2,…,N}，根据嵌入维数m及时间延迟τ可构造一批矢量X，即X=[Xi,Xi+τ,Xi+2τ,…Xi+(m-1)τ],(i=1,2,…,M)，其中N为时间序列长度；Xi为相空间中矢量；M=N-(m-1)τ为相空间矢量个数。

因此，对一维混沌时间序列进行重构可将其映射到高维空间[13-14]。通过该方法，可以在高维相空间中构造一批矢量：

(4)

嵌入维数m及延迟时间τ的选取对重构相空间至关重要[15]。定义差量为

ΔS(m,τ)=max{S(m,r,τ)}-min{S(m,r,τ)}

(5)

局部最大时间t对应S(m,r,τ)零点或ΔS(m,τ)最小值，时间序列延迟τd对应最大局部时间t中第1个，此时重构空间点最接近均匀分布，吸引子在相空间完全展开，据第一个局部时间确定时间序列延迟τd，进而据τd=ττs确定延迟时间τ与m值。

相空间重构可实现在更高维空间中恢复系统吸引子，便于找出系统的内在规律。典型的Lorenz和Rossler信号系统二维相空间重构混沌吸引子形态如图1所示，吸引子状态可用来判定时间序列是否具有混沌特征。

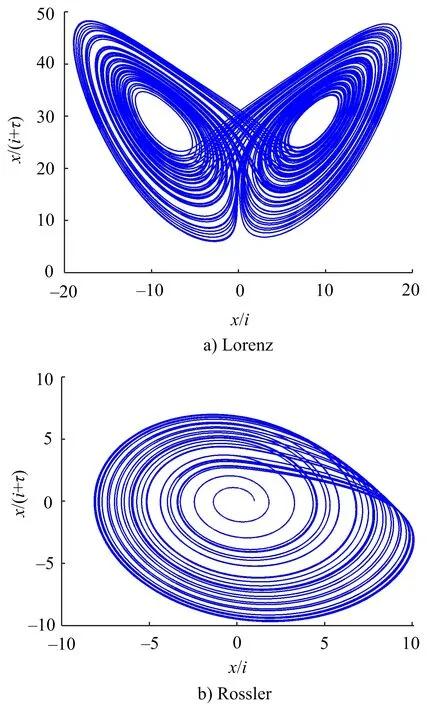
图1 典型信号的二维相空间重构吸引子Fig.1 Two dimension phase space constructed attractor of typical signal

2 爆破信号采集与重构

2.1 隧道位置

新悬泉寺隧道位于剥蚀侵蚀山区，地势陡峻，隧道起止里程为DK20+494.77～DK21+378.00,为全长883.23 m的单线电气化铁路隧道。隧道最大埋深约190 m，左侧距既有太岚线铁路隧道中心线最小距离为14 m。进口端岩石陡直，与悬泉寺桥台相连，出口端位于弱风化石灰岩层。隧道进口线间距为30 m，出口线间距为68 m，隧道距离汾河二库景区千年古刹悬泉寺最近距离为200 m。

该隧道掘进断面41.2 m2，采用钻爆法施工，为了最大程度降低爆破对周围既有构筑物的影响，采用双楔形掏槽+光面爆破形式，使用2#岩石硝铵炸药，炮孔直径32 mm。在隧道小净距处，采用“短进尺+弱爆破”方案，掏槽孔深度1.5 m，其余炮孔1.2 m，单循环总装药量为56.2 kg。隧道掘进岩层瓦斯含量较低，可选用MS1～MS15段电雷管跳段起爆，为爆破振动控制提供了良好的前提条件。

2.2 爆破信号获取

考虑到测试的便捷和持续性，在既有隧道避车硐内布置测点对爆破过程进行监测，既保证了测试数据的准确性，又减小了测试过程对既有隧道正常运行的影响。测试选用四川拓普测控生产的UBOX-5016型爆破测振仪，隧道雷管段别丰富条件下爆破信号具有宽频多峰值的特点，监测时设定拾振传感器采样频率为10 kHz，根据采样定理，其Nyquist频率则为5 000 Hz，保证数据测试的精度。既有隧道避车硐内测振传感器具体安装如图2所示。测点布置时，在避车硐与隧道掏槽中心平齐的位置设置测试平台，利用膨胀螺栓将角钢固定，将传感器固定在角钢预留的三个定位孔中，定位孔间要留有合适的间距，防止三向传感器在测试过程中相互触碰而导致信号失真。

图2 隧道现场测点布置Fig.2 Layout of measuring point in tunnel site

三向传感器准确记录了隧道爆破过程中不同方向的振速信息，通过对比发现沿隧道轴线方向的水平径向振速较其他两方向大，且信号辨识度更高。原因在于隧道爆破过程中破碎岩体质点运动方向与隧道轴线平行，导致该方向产生的振速值较大。因此，选择该方向的振动信号作为分析对象更具代表性。

爆破信号水平径向分量时程曲线如图3所示，其峰值振速为3.36 cm/s，对应时刻为9.8 ms，主振频率为127.42 Hz，波形图清晰展示了各段别雷管起爆产生的的振动响应形态。对于多段别爆破信号而言，毫秒延时致使隧道爆破信号必定为一个时滞的非线性系统。这种时滞系统通常具有多自由度、高维度特性，在系统的演化过程中，会伴随着混沌现象的产生。由此可见，爆破信号系统是高维的动力学系统，蕴含着复杂的特征信息，需重构到高维空间才能解析。

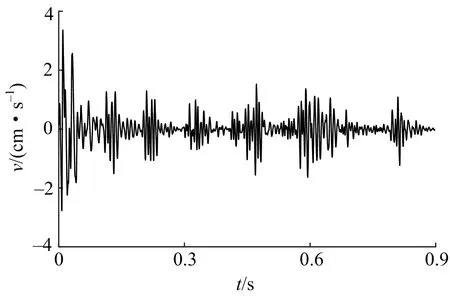
图3 隧道爆破振动信号时程(水平方向)Fig.3 Time history of blasting vibration signal in tunnel(horizontal radial)

混沌行为是由于信号内部的非线性特征，使得系统的演化行为具有随机性，因此其功率谱是宽频的连续谱。求取图3中信号功率谱分布如图4所示，其功率谱幅值在信号主振频段后以指数次幂急剧降低，体现出明显的混沌特征。从功率谱中可以看出信号中包含大量的动态噪声，谱中的峰值紧密交错并相互关联，具有混沌信号“噪声背景”和“宽频带”典型特征，可以直观判定爆破信号具有混沌行为。

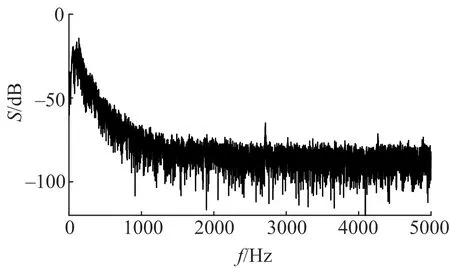
图4 爆破信号功率谱Fig.4 Power spectrum of blasting signal

2.3 信号频带划分与重构

由功率谱分布可知爆破振动信号能量主要集中在中低频段(500 Hz以下)，因此，采用FSWT对信号子频带重构时也以500 Hz以内频带为主。以100 Hz间隔为一个划分区间，500～5 000 Hz高频段作为一个独立区间，这样便可将信号划分为6个子频带子信号，获取每个子频带区间的重构信号如图5所示。从各子信号曲线可知：在各个子频带内，信号峰值振速逐渐降低，说明振动强度均随频率的升高而不断降低，对岩体破坏起主导作用的频率集中在500 Hz以内，计算能量占比为92.5%。500～5 000 Hz频带重构子信号振幅明显减小，主峰不明显且频率成分增多，为高频干扰成分。信号经FSWT分解逆变换重构后一定程度上起到了滤波作用，得到的各频带子信号波形光滑度提高，有效抑制了噪声并较好恢复了各频带子信号的波动形态，体现了信号重构的有效性。

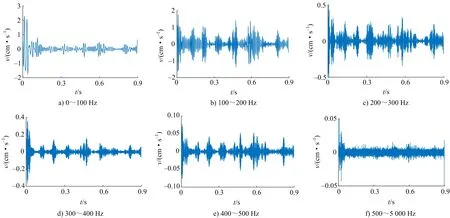
图5 各频带重构子信号波形时程Fig.5 Time history of each frequency band reconstructed sub-signal

3 爆破振动吸引子混沌特征

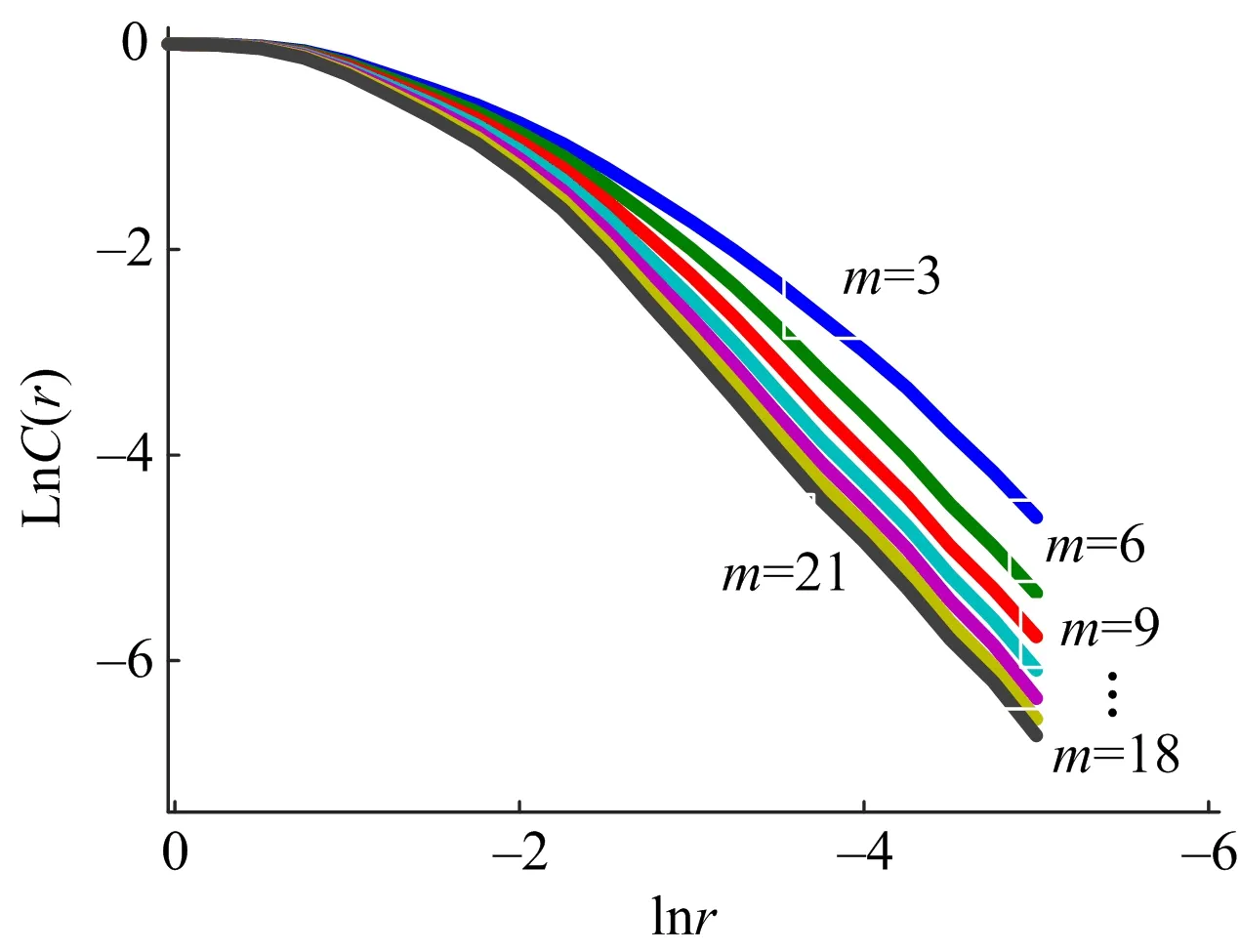
图6 不同嵌入维数lnC(r)-lnr双对数关系Fig.6 Double logarithmic relationship of lnC(r)- lnr with different embedded dimensions

3.1 嵌入维数的确定

隧道爆破信号具有混沌和分形的特征，关联维数是最基本的分形特征参数，这里采用虚假临近点法选取嵌入维数m[14]。对原信号选取不同的嵌入维数m，计算并绘制出lnC(r)-lnr的双对数关系曲线如图6所示。通过对图中曲线进行直线拟合得到的斜率即为关联维数D。当嵌入维数m由小变大时，关联维数D也具有相同的变化趋势。当m增大到9时，双对数曲线趋于平行，即D趋于饱和，从而确定嵌入维数m为9。

3.2 延迟时间的确定

延迟时间τ通常采用自相关函数法求取，设{x(i)}为一组实测时间序列，则其自相关函数为[15]

(6)

(7)

根据上式可构造τ与C(τ)函数，当C(τ)下降至(1-1/e)*C(0)值以下时所对应的τ为最佳延迟时间。

3.3 相轨迹图变化规律

常用的判别信号混沌特性的方法有吸引子轨迹法、功率谱法及 Lyapunov指数法。这里选用吸引子轨迹状态来表征爆破信号时间序列的混沌特征。将前述频率划分区间重构子信号分别进行相空间重构，运用主矢量法将其投影到二维坐标系中，通过相空间轨迹图的变化可直观清晰地展现各频率子信号系统状态的演变过程。根据前述理论，选择信号系统嵌入维数m=9，最佳延迟时间τ=3，通过C-C法进行信号相空间重构并得到子信号的吸引子形态变化过程如图7所示。

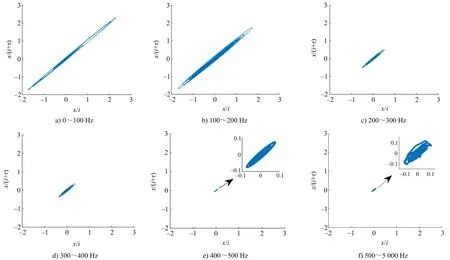
图7 不同频带重构子信号混沌吸引子演化过程(100 Hz间隔)Fig.7 Chaotic attractor evolution process of reconstructed sub-signal in different frequency bands (100 Hz interval)

从图7中可知：爆破信号各频带重构子信号吸引子为向内不断旋进的椭圆轨迹，子信号均具有明显的混沌特征，吸引子在二维相空间形态为沿相平面45°线为对称轴，外观包络呈类似“枣核状”的椭圆形分布。随着频率的增大，吸引子长短轴之比逐渐减小，在相空间形态趋于稳定，并最终汇聚在(0,0)坐标所在的中心不动点。

图7f中高频信号吸引子形态与500 Hz以下的形态发生逆转突变，不再具有低频段展开过程中的拓扑形态，反映爆破信号混沌系统有界性。在对应的吸引子状态出现相互排斥的奇异性,表现为折线形式，体现了不稳定的高频振荡特性，反映了爆破信号混沌系统在高频分量中的随机性。相空间内吸引子从低于主振频率的发散突变模式到主振频带的紧凑密实的稳态模式，再到高于主振频带的发散突变模式的演化分布规律。

为了进一步了解吸引子变化规律，取50 Hz为间隔的子频带做细化分析，重新获得不同频带重构子信号波形曲线(见图8)。

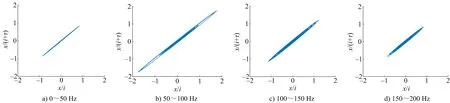
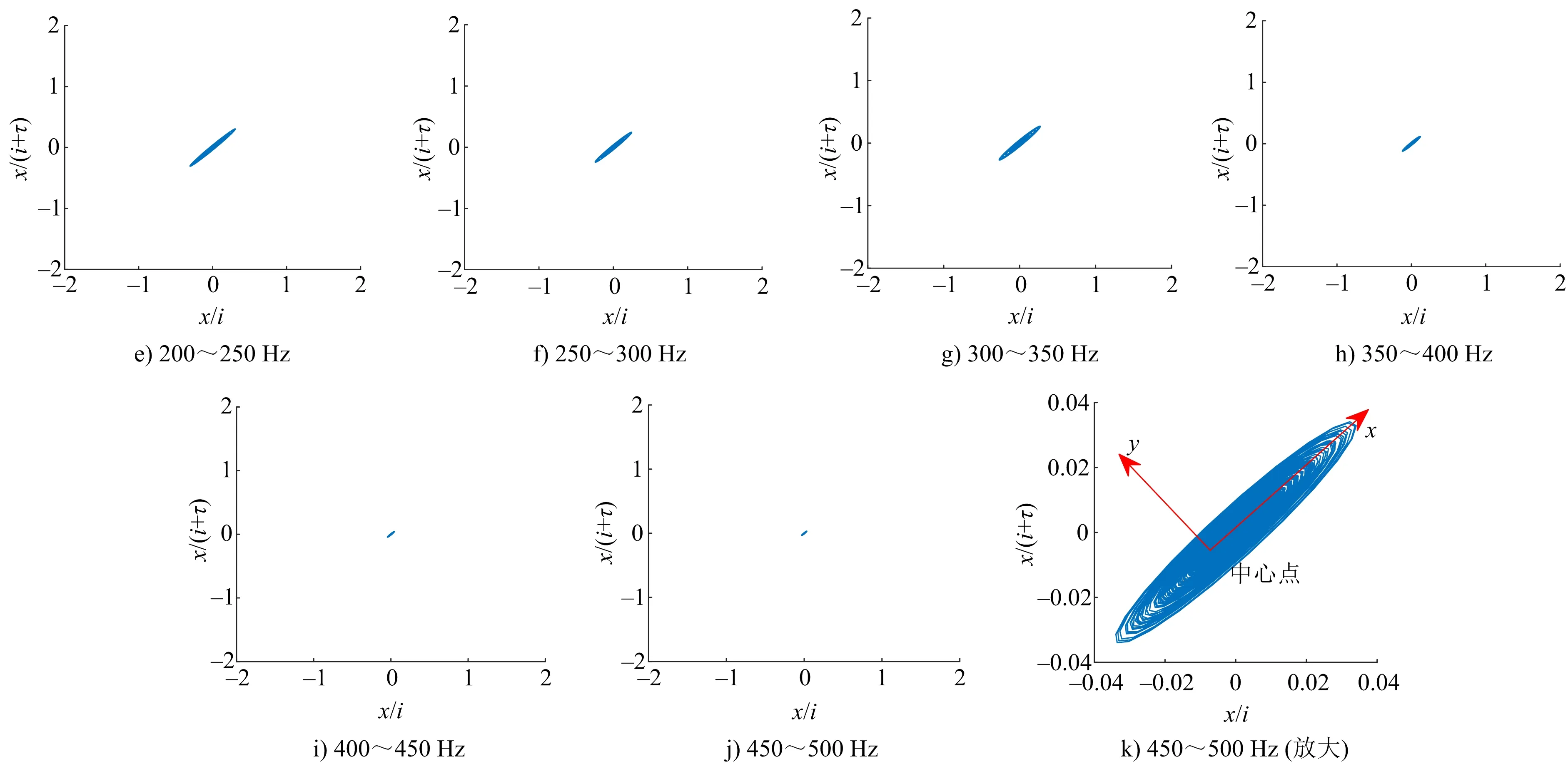
图8 不同频带重构子信号混沌吸引子演化过程与细节特征(50 Hz间隔)Fig.8 Evolution process and detail characteristics of chaotic attractors for reconstructed sub-signals in different frequency bands (50 Hz interval)

隧道爆破信号的优势能量位于主振频带范围内，重构子信号吸引子以主振频带为界限，两侧频率区间内信号吸引子在二维相空间的精细程度和收敛程度均出现明显不同。各频带重构子信号的混沌吸引子聚集在相空间的有限域内，其形态为具有无穷嵌套自相似结构的不相交环面组成，每个环面吸引子反映了不同频率信号混沌弥散状态，如图8k细节图所示。

吸引子在二维相空间中的覆盖面积大小反映了信号本身的复杂程度，也体现出信号能量的聚集和耗散状态。各频带重构子信号振速最大波峰和波谷值与相空间中吸引子椭圆长轴端值对应，表现出良好的局部化混沌特征，突出了有效信号的细节，反映了爆破信号系统混沌吸引子对振幅初值的敏感性。为了量化对相空间吸引子形态特征的评价，提取不同频带重构信号混沌特征参数如表1所示。

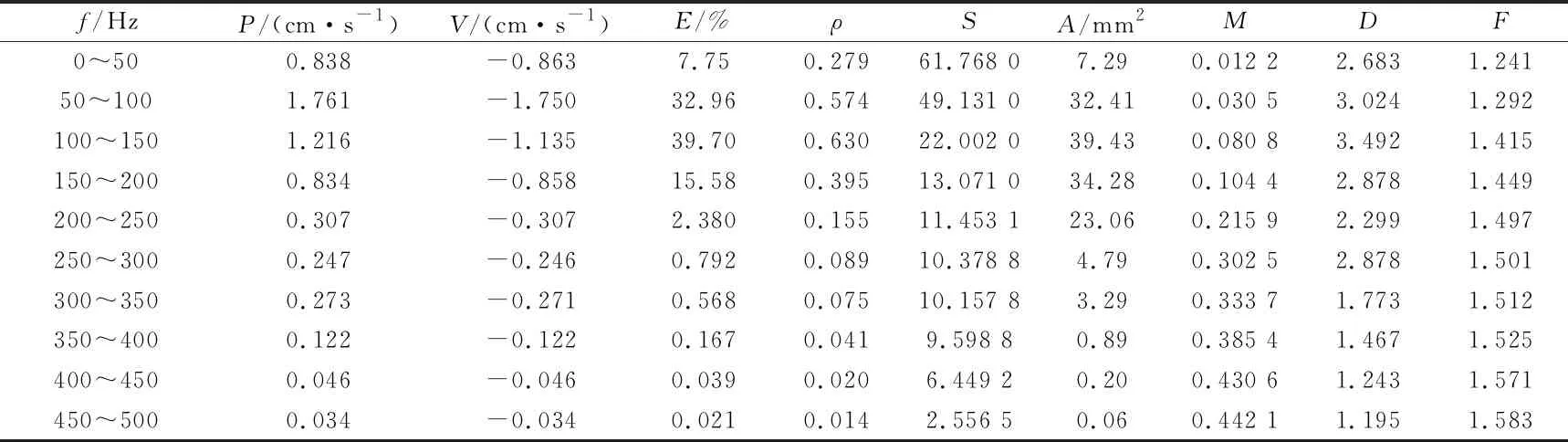
表1 不同频带重构信号混沌特征参数

隧道爆破信号不同频带子信号均为非稳态信号，由于子信号吸引子轨迹具有自相似性，分形维数可反映其轨迹所具有的结构特性。非整数的分形维数表征了爆破信号在不同频率区间混沌演化行为。爆破子信号具有复杂的内部结构，且不同频带子信号的混沌吸引子自相似性质说明了其非线性特征具有相对稳定性。在主振频带区间，炸药爆炸作用最为强烈，能量百分占比高，混沌特征也最为明显，体现在关联维数值较大为3.492。之后随着频率的增大，由于岩体介质的滤波耗能作用，影响爆破信号系统性能的因素减少，系统混沌特性不断减弱，关联维数逐渐降低，在450～500 Hz区间仅为1.195。随着频率的增加，主振频带以上子信号与原信号的相关系数减小，表明其与原信号的相关程度降低，杂波干扰越多，混沌特征更加微弱，信号的可预测性越小。最大lyapunov指数是衡量爆破信号动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率，是衡量信号非线性特征的一个重要指标。计算得到的最大李雅普诺夫指数值与频率的增加呈正相关，说明频率越高其吸引子在相空间越收敛，在相空间的聚集程度也更强，含有的损伤能量亦越少。

以主振频率所在的区间(100～150 Hz)为界限，在相对低频段(小于150 Hz)随着频率的逐渐升高，子信号振幅的波峰和波谷值也不断增大，峰值差、能量百分比及互相关系数也呈现相同的趋势，反映了不同段别雷管起爆在相对低频段内能量的不断补充。在相对高频段(大于400 Hz)随着频率的逐渐升高，子信号振幅的波峰和波谷值也不断降低，峰值差、能量百分比及互相关系数同样逐渐减小，反映了爆炸能量在相对高频段内的不断耗散，说明爆炸能量主要集中在低频信号，同时高频信号所包含的能量贡献也不可完全忽略。信号能量百分比E、相关系数ρ、吸引子包络面积A和关联维数D均以主振频带区间为拐点，呈现先增大后减小的规律，反映了爆破信号系统混沌吸引子对主频初值的敏感性。吸引子椭圆轨迹长短轴比S、最大李雅普诺夫指数M和分形维数F随着频率增大其值也不断增大，表明在有限的频率区域内，吸引子形态变化趋势较为稳定，吸引子特征参数值的变化可敏感地捕捉到信号的细节特征。

由上述分析可知，吸引子包络面积越大，该频段信号幅值越大，能量占比也越高；信号主频位于吸引子形态发生突变的频带范围内，振动在持续时间轴上分布越均匀，吸引子聚集程度越高。吸引子形态变化与爆破信号幅值、主频和持时之间有密切的关系，为隧道爆破信号主频、振幅、持时等特征参量的预测和判别提供依据。

4 结论

1)在同一测点三向振速中，通常与隧道掘进轴线平行的水平径向振速最大，这与掏槽孔单自由面起爆抵抗线方向和破碎岩体质点运动方向关系密切。

2)频率切片小波变换不受小波基选取的局限，自适应性强。重构信号具有很好的去噪、信号特征提取和细节保持能力，重构子信号对原始信号能量的贡献率与相关系数具有一致性，可用于信号波形特征的定量描述和分类判别。

3)隧道爆破信号具有明显的自相似分析特征，通过吸引子混沌动力学相轨迹图，可揭示隧道爆破不同频带信号在相空间的混沌特征演化规律。隧道爆破混沌系统具有初值敏感性、有界性和随机性的内在特征。混沌吸引子的演化规律揭示了隧道爆破混沌动力学特性，体现了其非线性动态变化机制，为隧道爆破信号主频、振幅等特征判别提供依据。