不同装药结构的双向聚能药包爆破数值研究

吴 波，韦 汉，徐世祥，黄劲松，张景龙，李华隆

(广西大学土木建筑工程学院，南宁 530004)

聚能装药结构不仅在军事领域得到了广泛的应用，而且在工程爆破领域也得到了越来越广泛的应用，例如隧道、巷道及边坡的定向断裂爆破。关于定向断裂控制爆破，国内外学者开展了大量的实验与实践研究。李清等[1]采用数字激光动态焦散线系统研究不同药量的切缝药包双孔裂纹扩展规律。杨仁树等[2]采用高速纹影和损伤测试技术研究切缝药包爆轰波和爆生气体的传播机制，并探讨了不同药量对岩体损伤的影响。此外，杨仁树等[3]还通过高速纹影和空气冲击波超压系统对不同管制材料的切缝药包爆轰波与爆生气体的传播机制进行了研究。张盛等[4]通过井下爆破实验对D型聚能管装药量、封堵长度、装药结构、炮孔间距等影响预裂爆破效果的因素进行了研究。

随着科学技术的发展，计算机的应用也越来越广泛，数值模拟成为了继实验与理论研究的第三种重要的研究方法。不少学者在聚能装药结构方面也进行了大量的研究,比如对切缝药包爆破参数的优化研究。杨建辉等[5]对切缝药包聚能管的厚度、切缝宽度进行研究，建立单、双孔模型对爆炸应力变化进行分析。岳中文等[6]采用数值模拟与实验相结合的方法来研究炮孔间距对切缝药包裂纹扩展规律的影响。申涛等[7]基于ALE算法研究切缝药包爆炸过程压力场、冲击波和切缝管动态变化，从而揭示切缝药包爆炸作用机理。王雁冰[8]基于LS-DYNA研究切缝药包爆轰和初始裂纹的形成，以及不耦合系数与爆破损伤之间的关系。李必红等[9]通过数值模拟与实验相结合研究椭圆双极线性聚能药包的最优不耦合系数，数值模拟与实验得出的最优不耦合系数分别为3.20、3.43，两者基本一致。张先锋等[10]也通过ALE对3种不同典型线性装药的聚能射流形成及侵彻过程进行了数值模拟。何满朝等[11]基于双向聚能拉张爆破理论对巷道炮孔间距进行数值优化，并将数值结果应用于实际工程验证其有效性。

以上对聚能药包的研究大都基于有限元，然而基于有限元Lagerange方法容易造成网格的畸变而使计算终止，基于ALE算法又不易对物质边界捕捉，甚至有时网格畸变严重时亦造成计算终止。因此不少学者着手于无网格来研究聚能药包的爆轰过程，尤其是最早提出的SPH无网格方法。SPH方法最早于1977年由Lucy等[12]提出并将其应用于天体物理学，随后广泛应用于各个领域的研究，Swegle等[13]首次将其应用于水下爆炸数值研究，实现SPH在爆炸领域的应用。Liu M B等[14-15]基于SPH对无药型罩聚能装药爆轰过程及聚能射流形成过程进行研究。杨刚等[16]通过自编程序实现的SPH，在装药质量、药型罩质量和装药宽度相同的情况下，对不同药型罩作用下单向聚能无外壳药包聚能射流的形成及后效侵彻过程影响进行分析。李磊等[17]基于三维SPH、FEM及理论计算对比分析聚能装药射流，并将SPH与FEM耦合分析聚能射流侵彻钢靶的过程，并与实验相比较验证耦合算法的有效性。

椭圆长短轴比为15∶11时可实现EBLSC药柱聚能方向能量的充分利用，目前工程实践普遍采用的聚能管型号为长轴∶短轴=30 mm∶22 mm。基于SPH和ALE方法，在保证椭圆长短轴比为15∶11和长轴为30 mm的情况下，分别对药型罩及外壳为紫铜、PVC的椭圆双极线性双向聚能药包(EBLSC)锥角参数进行优化，验证不同聚能管材料的聚能药包变化规律是否一致，最后就不同外壳形状对聚能装药射流头部速度的影响进行分析。

1 材料模型

1.1 炸药模型

本文选用LS-DYNA中常用于模拟爆炸的MAT_HIGH_EXPLOSIVE_BURN模型来描述炸药的本构关系，并采用JWL状态方程表述炸药压力与体积的关系：

(1)

式中：p为压力；V为体积；A，B，w，R1，R2为状态方程基本参数；E为单位体积爆轰能，炸药本构参数及状态方程参数参照文献[16](见表1)。

表1 炸药本构参数及状态方程参数

1.2 聚能管模型

聚能管主要由药型罩及外壳两个部分组成，药型罩与外壳选取相同的紫铜材料，相应的材料模型为MAT_JOHNSON_COOK模型，对应的状态方程为EOS_GRUNEISEN：

(2)

表2 聚能管材料本构参数

表3 聚能管状态方程参数

当聚能管材料选取PVC材料时，由于PVC是一种热塑性材料，温度升高一定程度之后会发生相变分解成HCl气体，具体表征PVC材料的力学及物理特征相对困难。由于爆炸的瞬时性，在爆轰波及爆生气体挤压药型罩形成聚能射流时可认为该过程PVC未发生相变。故PVC材料可选用随动硬化模型MAT_PLASTIC_KINEMATIC来表征材料的力学变化，PVC聚能管物理力学参数[11]如表4所示。

表4 PVC聚能管物理力学参数

1.3 空气模型

本文在SPH模拟中忽略空气对聚能射流的影响，在ALE模拟时考虑空气的作用将炸药能量向外传播，空气密度为0.001 25 g/cm3，对应的状态方程同样为EOS_GRUNEISEN，其状态方程参数如表5所示。

表5 空气状态方程参数

2 数值模型

为研究药型罩锥角大小对双向聚能药包爆破聚能射流的影响，在保证长短轴比为 15∶11和长短轴不变的情况下，建立不同锥角大小的椭圆双极线型聚能药包，不同锥角的四分之一SPH模型如图1所示。

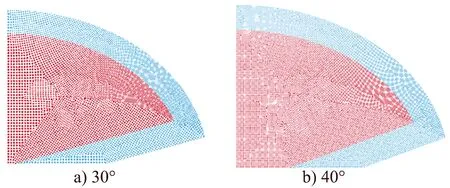
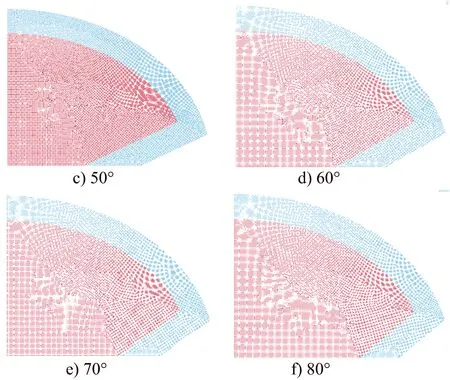
图1 不同锥角的四分之一SPH模型Fig.1 Quarter SPH model with different cone angles

为研究外壳形状对聚能射流头部速度的影响，建立常规聚能药型罩锥角为70°下不同外壳形状的聚能药包，四分之一ALE模型如图2所示。

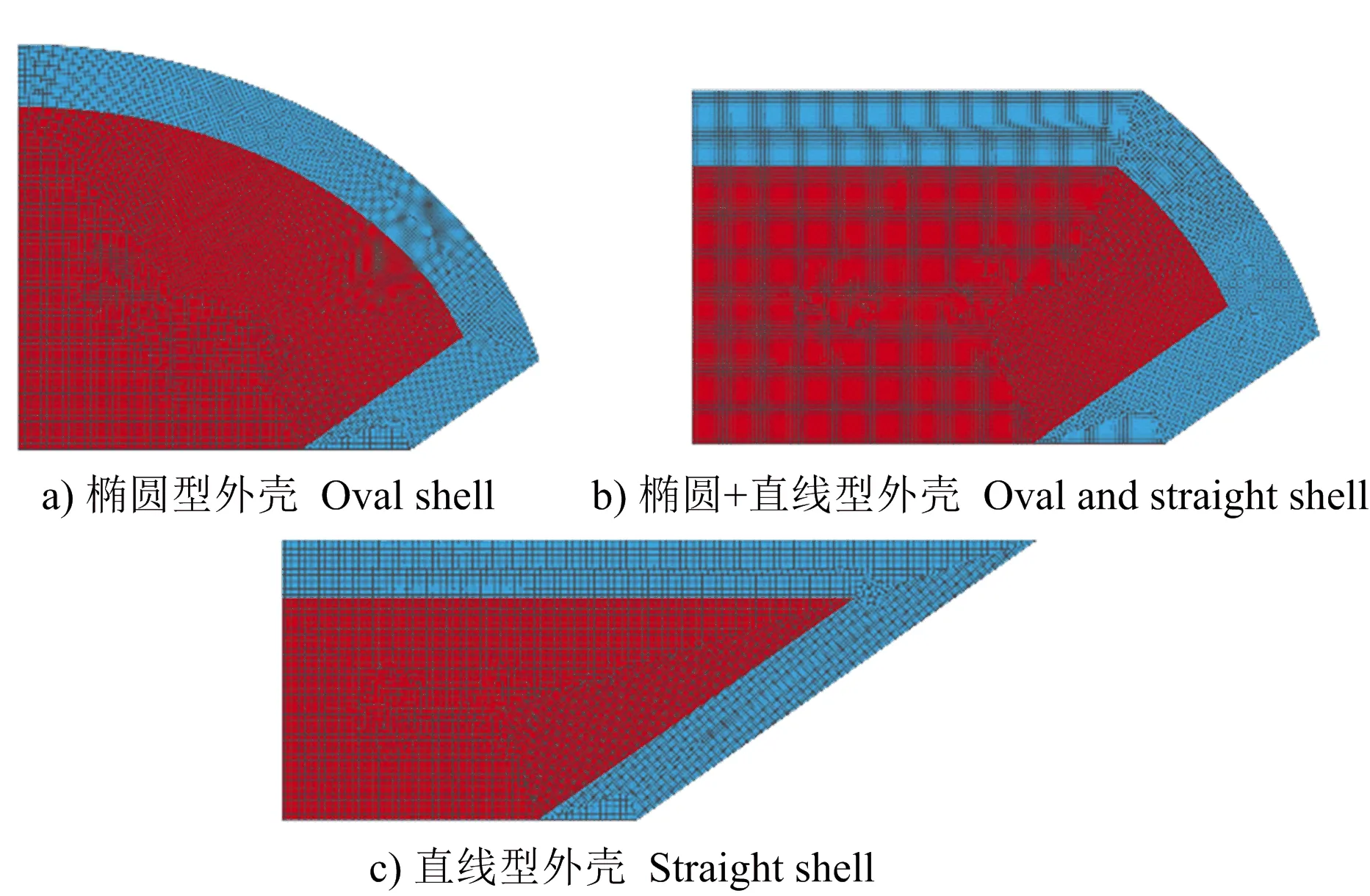
注：b)是a)的基础上，减去部分药量，将上部椭圆外壳改为直线型外壳；c)与a)装药面积一致，但c)的药型罩长度较a)的长。图2 不同外壳的四分之一ALE模型Fig.2 Quarter ALE model of different shells

所建立模型均采用四分之一模型，并施加对称边界加以约束，实现的SPH粒子间距为0.008 ～ 0.01 cm，实现的ALE算法在炸药附近网格平均尺寸为0.01 cm，炸药向外扩张，网格逐渐过渡到0.05 cm，并施加无反射边界条件。

3 数值结果及分析

3.1 锥角影响分析

由不同锥角聚能药包在t=10s时刻的速度云图(见图3)可知，不同药型罩锥角聚能药包在两种算法中聚能射流形态和最大平均射流头部速度基本一致，表明所实现的两种算法的有效性和可行性，但ALE算法无法捕捉射流边界形态，在射流形态上较SPH算法模糊。此外，随着聚能药型罩锥角的不断增大，聚能射流头部速度不断减小，在同一时刻形成的射流长度也在不断的减小，形成杵体的药型罩质量分数也在不断减小，用于形成射流的药型罩质量有所增大，表明药型罩锥角的大小对聚能射流的形成及头部速度有显著影响。当聚能射流头部速度大时，而大部分的药型罩用于形成杵体，所实现的侵彻效果不一定最佳。

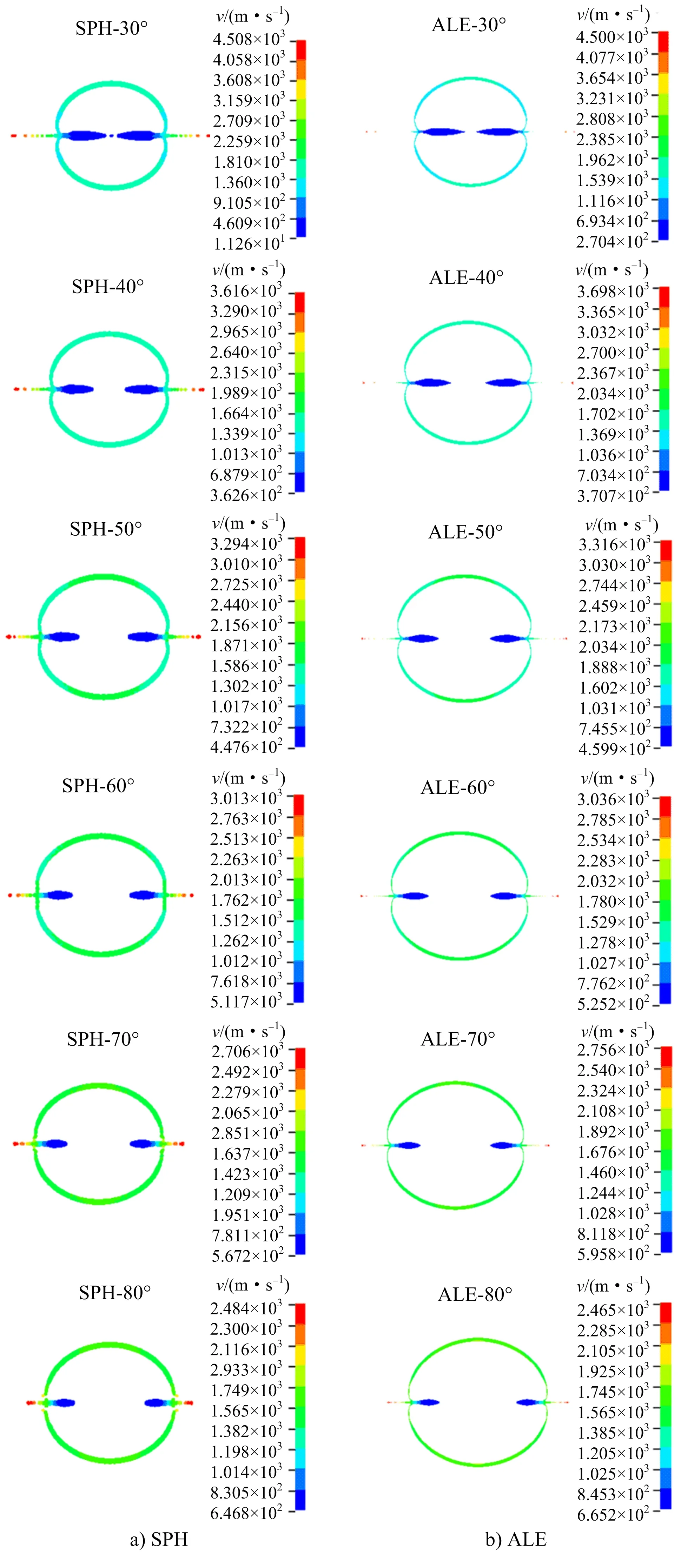
图3 t=10 s时不同锥角的聚能药包速度云图Fig.3 Cloud of shaped charge velocity with different cone angles at t=10 s

3.2 SPH和ALE算法影响分析

由不同锥角聚能药包在SPH和ALE算法下射流头部平均最大速度随时间变化曲线(见图4)可知,两种算法计算的射流头部平均最大速度值在射流形成初期有一定的误差，随着射流不断拉伸，射流不再受杵体的拖曳作用后，射流头部速度趋于稳定，两种算法趋于一致。SPH方法在计算过程中未考虑空气的影响，ALE算法必须考虑空气作为能量传递介质，但两者计算结果趋于一致，表明空气对两种算法的影响很小，为减少计算量，SPH算法不考虑空气的影响是可行的。由图4可知，各锥角药包射流头部速度时间变化曲线形态一致，在短时间内迅速上升，后下降再趋于稳定，下降段主要是因为射流尾部对射流头部的拖曳作用造成的[18]。计算过程中发现，初始光滑粒子数和光滑长度对SPH算法计算结果较为敏感，网格的大小和走向对ALE算法有一定的影响，故两种算法在计算结果上存在一定的误差，但均在可接受范围内，表明数值模拟方法的有效性。随着药型罩锥角的减小，聚能射流趋于稳定后的头部平均最大速度值增大，当药型罩锥角减少到30°时，最终稳定射流头部速度为4 500 m/s，表明药型罩锥角对聚能射流有显著影响。

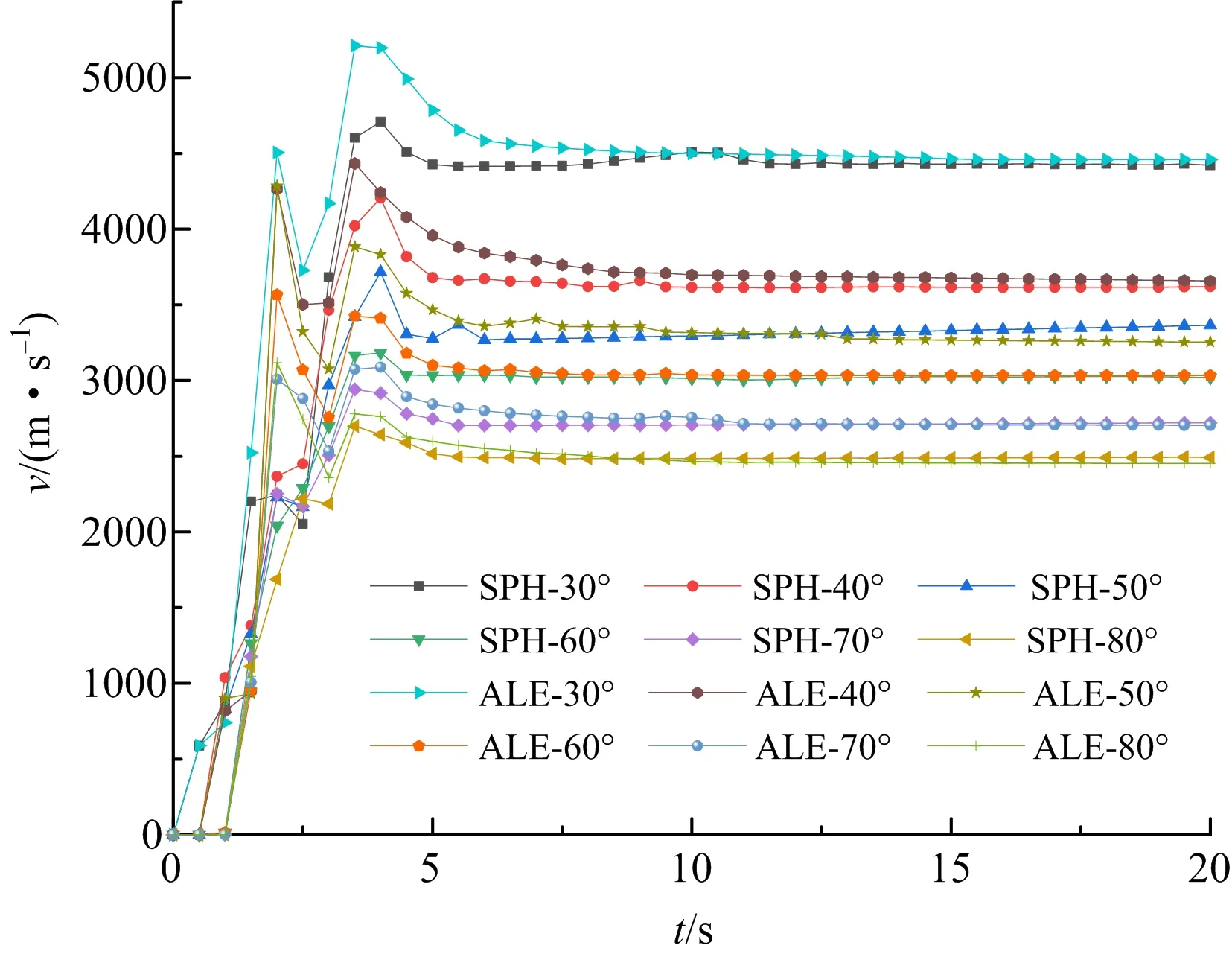
图4 射流头部速度时间历程Fig.4 Time history of jet head velocity

由不同药型罩锥角的聚能药包形成的聚能射流头部至杵体尾部长度随锥角的变化关系(见图5)可知，随着锥角的增大，所形成的射流长度在不断的减小，再次证明了药型罩锥角对聚能射流的影响。在优化椭圆双极线型聚能药包时应适当减小锥角大小，可以减少炸药用量，同时在一定程度上增大射流头部速度，但锥角过小会造成大部分药型罩质量用于形成杵体，不利于后续高速射流的持续侵彻作用。两种算法在射流长度上存在一定的波动，最大误差值发生在药型罩锥角为30°的聚能药包，误差为8.3%，但均在可接受范围以内。

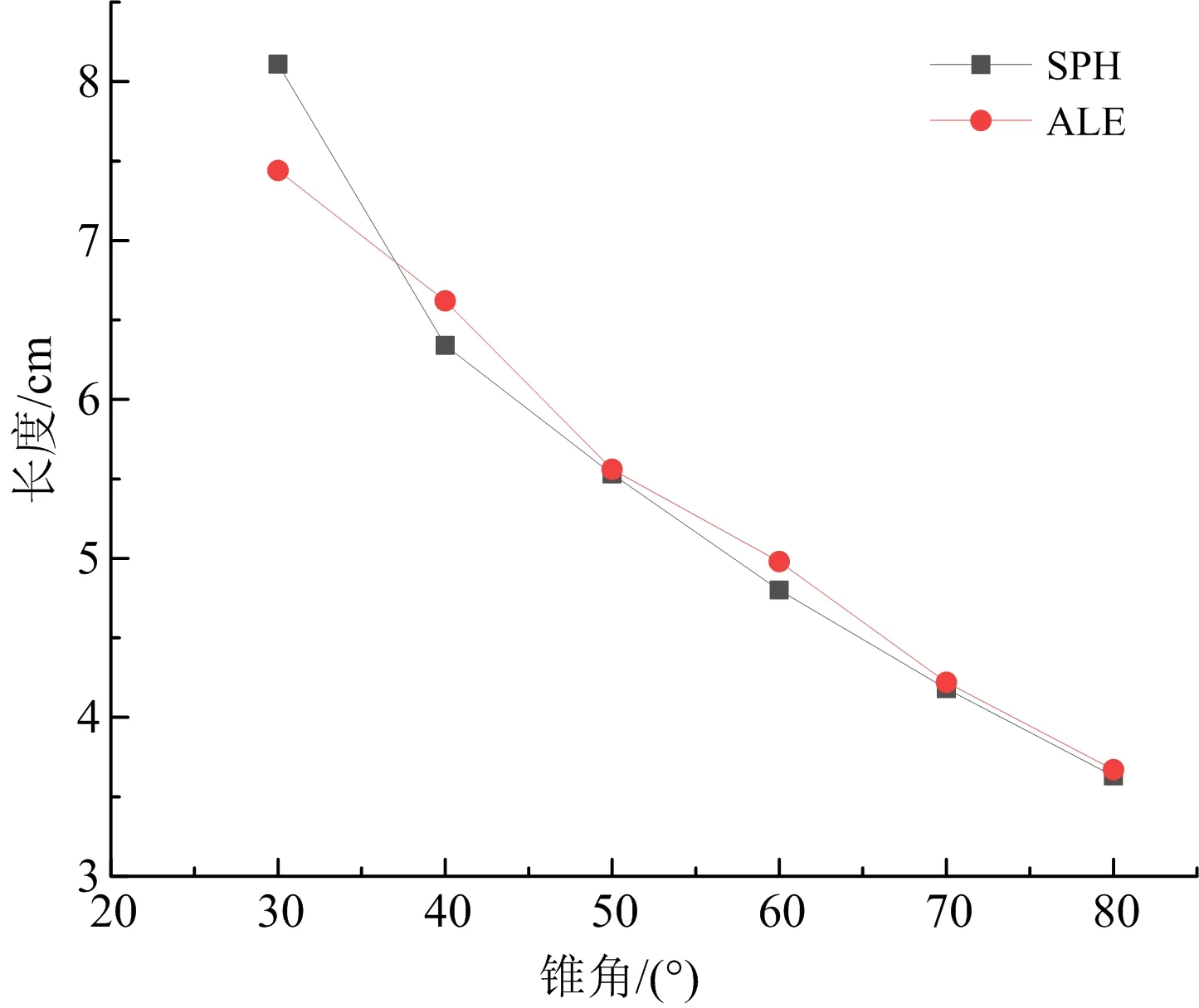
图5 射流长度随锥角变化关系Fig.5 Change relationship of jet length with cone angle

3.3 外壳材料的影响分析

为对比不同材料的聚能管锥角变化时聚能效应是否有相似的变化规律，由于篇幅的限制，聚能管材料为PVC时只进行了ALE的计算分析。不同锥角的聚能药包在t=10s时刻的速度云图如图6所示，不同锥角的聚能药包爆破聚能射流速度时间历程如图7所示。

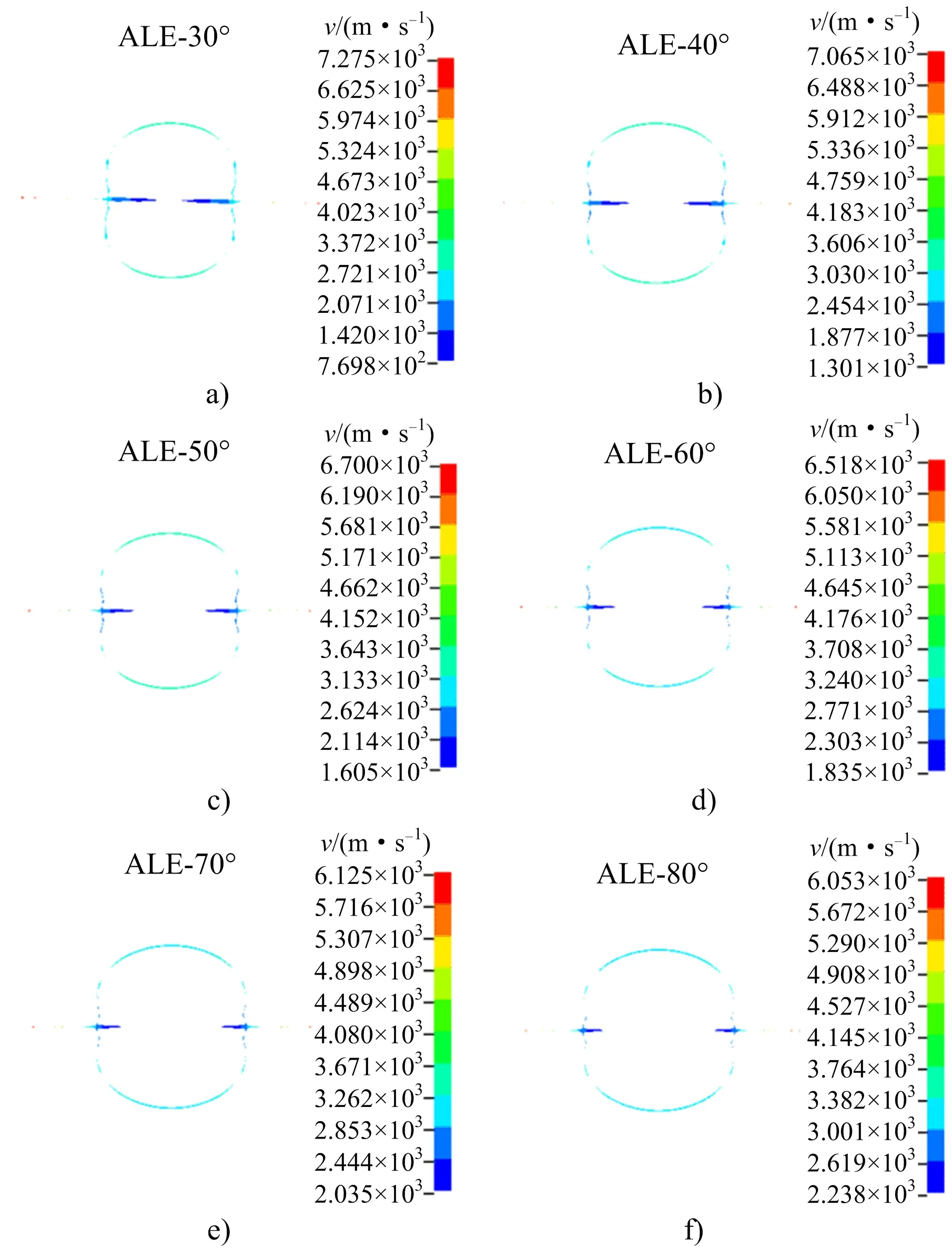
图6 不同锥角的聚能药包在t=10 s时刻的速度云图Fig.6 Velocity cloud of shaped charge with different cone angles at t=10 s

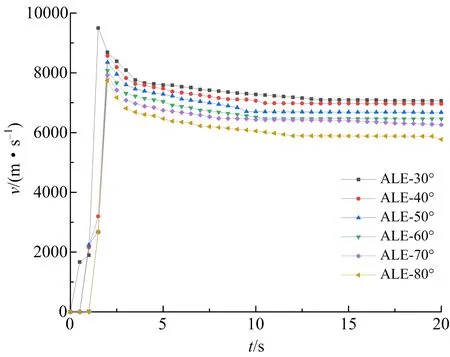
图7 不同锥角聚能药包爆破聚能射流速度时间历程Fig.7 Time history of jet velocity of shaped charge with different cone angles

由图6可知，在t=10s时随着药型罩锥角不断增大，装药面积逐渐减小，聚能射流头部速度不断减小，与聚能管材料为紫铜的变化规律一致。同时不同锥角的聚能射流变化形态也基本一致，但不同药型罩锥角所形成的聚能射流和杵体所占药型罩的质量百分比有所不同。

由图7可知，通过射流头部速度随时间的变化规律来反映聚能射流的形成过程以及药型罩锥角改变对聚能射流的影响。在炸药爆轰之后，药型罩被迅速挤压形成聚能射流并很快达到最大速度，由于杵体速度与射流之间存在速度梯度，射流不断被拉长且射流头部速度不断减少，当射流与杵体分离之后射流头部速度基本维持在一个稳定状态。由于ALE算法考虑空气的影响，随着射流不断向外运动，有少量能量用于克服空气阻力，射流头部速度略有降低，但基本稳定。此外，随着药型罩锥角的不断增大，聚能射流头部最大速度平均值不断减小，再次验证了聚能管材料为PVC时聚能射流随锥角的变化规律同聚能管材料为紫铜时的变化规律是一致的。

3.4 外壳形状的影响分析

由t=20s时不同外壳聚能药包速度分布云图(见图8)可知，两种算法在该时刻形成的射流形态基本一致，且头部最大速度平均值也基本一致。椭圆型外壳和椭圆+直线型外壳在该时刻的射流头部速度大致为2 700～2 800 m/s，但椭圆+直线型外壳装药较椭圆型外壳要少，表明椭圆+直线型外壳装药结构优于椭圆型外壳装药结构。在实际隧道或边坡岩石的聚能爆破中可采用椭圆+直线型外壳装药结构，充分利用爆炸能量实现岩石定向断裂，同时防止非聚能方向岩体损伤破坏。椭圆型外壳和直线型外壳相比较可知，椭圆型外壳和直线型外壳装药量相同，但直线型外壳聚能药包实现的射流头部速度大于椭圆型外壳，表明直线型外壳装药结构优于椭圆型外壳，主要是因为直线型外壳中药型罩长度大于椭圆型外壳，能充分利用炸药能量实现定向聚能。

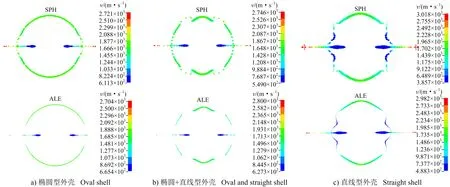
图8 在t=20 s时不同外壳形状聚能药包速度分布云图Fig.8 Cloud of velocity distribution of shaped charge with different shell shape at t=20 s

由不同外壳形状的聚能药包射流头部平均最大速度随时间历程(见图9)可知，椭圆型外壳聚能药包和椭圆+直线型聚能药包的最终稳定射流头部平均最大速度基本一致，但椭圆+直线型聚能药包装药量相对椭圆型外壳聚能药包要小，再次表明椭圆+直线型聚能药包装药结构优于椭圆型外壳聚能药包。直线型聚能药包最终稳定射流头部最大速度平均值明显大于前述两种装药结构，主要是因为在相同装药量情况下该装药结构的药型罩更长，能够充分利用爆炸能量实现聚能效应。在聚能装药爆破中尤其是采用椭圆双极线型聚能药包的聚能水压爆破，装药结构的参数优化对增大孔距、增大开挖进尺等具有一定的现实意义。通过对不同装药结构的聚能药包参数进行数值优化，分析结果可指导工程实践以及优化爆破参数。

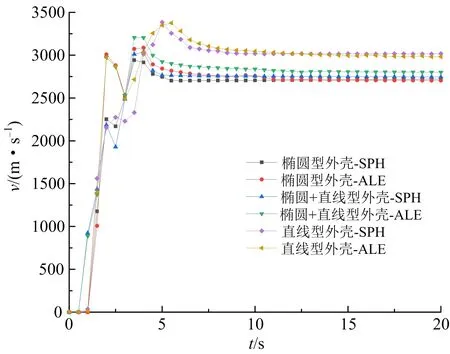
图9 不同外壳形状聚能药包爆破射流头部速度时间历程Fig.9 Time history of jet head velocity of shaped charge blasting with different shell shapes

4 结论

1)在保证长短轴比为15∶11、长轴为30 mm，药型罩为2 mm厚的紫铜材料的情况下，随着椭圆双极线型聚能药包锥角不断减小，装药面积逐渐减小，但聚能射流头部速度越大，变化规律也适用于聚能管为PVC的聚能药包。

2)不同锥角的聚能药包爆破形成的杵体和聚能射流所占药型罩的质量百分比不同，随着药型罩锥角不断减小，用于形成杵体的药型罩质量增大，用于形成射流的药型罩质量有所下降。

3)不同外壳对射流的产生效果不同，其中椭圆+直线型外壳和纯椭圆型外壳形成的聚能射流头部速度基本一致，但前者相对后者节省药量，此外两者形成的射流头部速度相对纯直线型外壳的要小。