煤岩体孔隙结构应力特征的数值模拟研究

王 刚，江成浩，陈雪畅

煤岩体孔隙结构应力特征的数值模拟研究

王 刚1,2，江成浩2，陈雪畅2

(1. 山东科技大学 矿山灾害预防控制省部共建国家重点实验室(培育)，山东 青岛 266590； 2. 山东科技大学 安全与环境工程学院，山东 青岛 266590)

为了探究不同加载方式下煤岩体孔隙周围的应力分布规律，通过CT三维重建技术构建含有不同孔隙形状的煤岩体骨架模型，并利用ABAQUS软件进行单轴、三轴压缩实验模拟。结果表明，球状孔隙结构在单轴压缩条件下，上下区域表现为拉应力集中，左右区域表现为压应力集中。不同倾角的椭球状孔隙结构其长短轴区域的应力集中类型不同。单轴压缩过程中，轴向加载速度影响球状孔隙周围的Mises应力峰值和1应力的变化；三轴压缩过程中，孔隙结构依然经历了压密、弹性、塑性和破坏4个阶段，较低的围压条件使得弹性阶段“应力–应变”曲线与“应力–时间”曲线高度重合。从微观角度为煤岩体力学研究提供了一种新的方法和思路。

CT三维重建；孔隙结构；数值模拟；单轴压缩；三轴压缩

近年来随着煤矿开采深度的增加，复杂的受力环境加剧了煤岩体的破坏过程，由此导致的冲击地压等灾害事故层出不穷。因此，煤岩体结构应力特征的研究越来越受到重视[1]。国内外学者主要从宏观、微观两方面对该问题进行探究[2-4]。由于岩石类材料的失效破坏可以看作是由微裂纹的扩展和聚结引起的[5-6]，因此，微细观角度下煤岩体应力、应变情况的研究对理解其失效机理尤为重要[7-8]。随着数字图像处理技术的逐渐成熟，SEM、CT等高精度成像设备被大量应用在岩石力学领域[9-11]。同时数值模拟技术具有的可重复性、不受外界环境干扰以及可获得全过程检测数据的优点，能够有效避免扫描和加载实验两者的非同步性对结果造成的误差，有助于实现多尺度条件下煤岩体结构应力特征的研究[12-15]。基于CT和数值模拟方法，Zhao Yixin等[16]在重建岩石模型的基础上建立了数值模型，模拟了几种煤样的单轴抗压强度UCS(uniaxial compressive strength)和P波速度。SUN Huafei等[17]采用高精度CT成像和三维重建方法构建了断续煤岩三维数值模型，模拟研究了卸载模式对煤岩力学性质及破坏机制的影响。复杂孔隙结构的存在是导致加载过程中煤岩体应力分布不均的主要原因，但上述研究中，缺乏对煤岩体微细观结构，特别是孔隙结构在不同加载方式下应力特征的研究。为了解决上述问题，笔者运用CT扫描系统对未受力状态下的煤样实施扫描，结合CT三维重建得到了含有微细观孔隙结构的煤岩体骨架模型，通过对三维煤体骨架模型布置不同的轴向加载速度和围压条件实现了单轴、三轴压缩实验模拟，从数值模拟角度研究不同加载方式下煤岩体孔隙结构的应力变化规律。

1 煤岩体结构的损伤破坏模拟

1.1 CT三维重建模型

煤岩体结构的三维重建过程如图1所示。采用μCT225kVFCB型高精度扫描仪对未施加外部载荷作用的某矿长焰煤试样进行CT扫描分析，得到尺寸为201 4 Pixel×204 1 Pixel、分辨率为2 μm煤岩体CT图像，其中能观察到的最小孔隙尺寸为2 μm。为减轻模拟过程的计算压力，在相同位置处批量裁剪连续的100张尺寸为100 Pixel×100 Pixel的CT图像，如图1a所示，模型的真实尺寸为200 μm×200 μm×200 μm，所能观察到的孔隙尺寸范围为2~200 μm。其次，基于Matlab中的图像读取函数提取该CT图像的灰度值矩阵，并制成数字地面模型(Digital Terrain Model，简称DTM)，如图1b所示，采用增设维纳滤波去噪的DTM阈值分割法确定图像阈值为30[18]。最后，将阈值分割后的CT图像导入基于Matlab语言的重建软件中进行三维重建，得到如图1c所示的煤岩体骨架结构模型。通过观察可以看出，煤岩体的孔隙多呈球状、椭球状、不规则多边形状杂乱地分布于煤体中，这体现出煤岩体真实微细观结构的非均质性。

图1 煤岩体骨架结构模型的构建

1.2 算法及破坏准则

将重建后的模型导入到HyperMesh软件中进行网格优化后，生成的inp文件导入到ABAQUS求解器中进行后续的模拟计算。选用能够克服复杂材料退化和失效问题的显式算法作为模拟的计算基础，同时，将整个模拟环境假设为准静态过程以获取任意加载时刻下各力学状态参量的准确值。为全面获取煤岩体的力学数据，将加载过程分为3个阶段，分别设置模型的本构方程和破坏准则：弹性阶段选择ABAQUS中的Elastic本构模型进行设置；塑性阶段采用考虑中间主应力影响的线性Drucker- Prager(D-P)准则对煤岩体结构的屈服形变进行描述；考虑到剪切–拉伸变化是煤岩体压缩过程中的主要破坏形式，设置最大拉应力、剪切破坏准则作为基体单元发生破坏的判别条件。

选用的线性D-P本构方程在π屈服面上的函数为：

式中：为等效围压应力；为中主应力对屈服的影响参数，取值范围[0.778,1]；为偏应力不变量；为材料的摩擦角；为材料的黏聚力，=(1–1/ 3tan)c；c为压应力；为围压。

选用的剪切–拉伸破坏准则方程表现形式为：

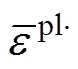
根据煤样自身的物理属性以及相关参数变化特征，确定本次模拟的物理参数：弹性模量为9.09 GPa；内摩擦角为51°；单轴抗压强度0.12为9.55 MPa；黏聚力为6.99 MPa；max为4.2 MPa；泊松比为0.26；为0.7；pls取0.001 5，s=pls=0。

1.3 边界设置与加载条件

煤岩体模型的边界约束设置如图2所示。首先，创建一刚性板结构与模型的上表面耦合接触，并对其设置初始速度模拟压头作用；其次，下表面布置位移约束防止加载过程中模型移动，同时4个侧面施加均布围压。由于存在刚体接触，煤岩体结构的上表面采用罚函数进行定义，其切向摩擦系数设置为1；侧面、下表面不涉及与其他物体的耦合接触，因此，设置无摩擦的接触形式。

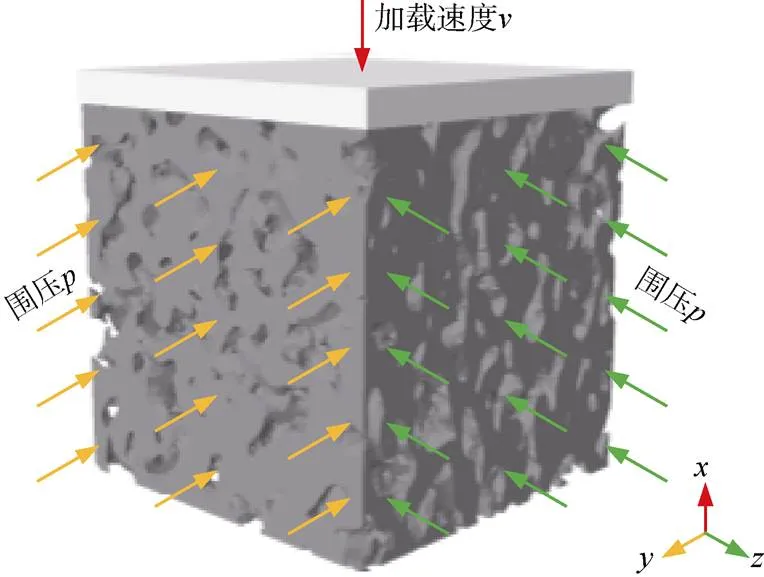
图2 模型加载

本次模拟设置以下2种方案：

①对压头设置轴向加载速度0，分别为0.010、0.015、0.020、0.025、0.030 mm/s，侧面不加围压；

②轴向加载速度0设置为0.02 mm/s，4个侧面分别施加0.20、0.25、0.30 MPa的围压。

2 不同形态孔隙结构应力特征

在微观视角下，孔隙结构形态复杂多变，其应力分布往往会受到倾角、形状等因素影响。由上述分析可知，球状和椭球状孔隙结构是煤岩体孔隙的重要组成部分，在煤岩体形变破坏中一直扮演重要角色。为清晰体现两种形态孔隙结构的应力分布，笔者选择煤岩体模型中与面平行的截面中球状和椭球状孔隙结构进行观测。

通过对该模型结构的分析，分别选择6个球状和椭球状孔隙进行应力研究。其中A1—A6为球状孔隙结构，B1—B2为椭球状孔隙倾角为0°的孔隙，B3—B4为椭球状孔隙倾角为45°的孔隙，B5—B6为椭球状孔隙倾角为90°的孔隙。按照图3所示的方式沿顺时针方向等角度布置测点，测取2种结构的主应力值。其中，为椭球状孔隙结构截面的长半轴，为短半轴。在此基础上，以0=0.02 mm/s单轴加载的方式为例，对孔隙结构的应力分布特征进行研究。

图3 孔隙中测点位置分布情况

2.1 球状孔隙

球状孔隙结构周围的主应力情况见表1。由表中可以看出，孔隙周围出现了不同类型的应力集中。上下边缘单元的1基本为正值，表现为拉应力集中分布，最大值不一定出现在上下边缘的中心测点上。3表现为负值的测点占总测点数的70%左右，3max出现在球状孔隙左右边缘单元上，而此位置对应的1也多为负值，即压应力在此集中分布。根据最大剪应力理论，单轴压缩过程中|1–3|与剪应力有关，其值为0.25~7.79 MPa，而最大值基本存在于球状孔隙结构的左右边缘区域。这与3的分布规律相似，由此可以得出压应力与剪应力之间存在密切联系。主应力2的正负关系与同位置处1值的变化规律类似，应力范围为0~4 MPa，但也有45%的球状孔隙出现负值应力的情况，其作用效果均低于主应力1和3造成的影响。

2.2 椭球状孔隙

利用ABAQUS软件模拟数据作出0°、45°、90°三种椭球状孔隙的主应力分布情况，如图4所示。暗青色轴表示椭球状孔隙中的长轴，绿色轴表示短轴。图中的黑色、红色、橙色变化曲线分别代表主应力1、2和3的变化规律。同时，对椭球状孔隙中相应的测点位置进行标注。

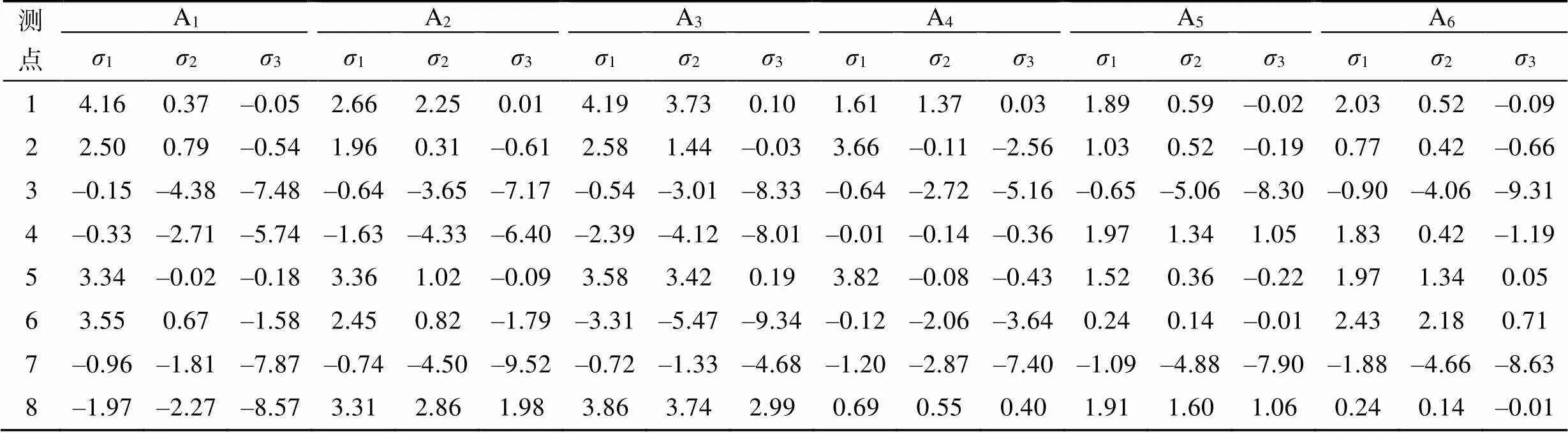
表1 A1—A6球状孔隙周围测点的主应力情况

当倾角为0°时，椭球状孔隙的长轴与加载方向平行，主应力1在孔隙的尖端附近(即长轴位置)表现为拉应力集中，随着测点远离尖端，1值逐渐减小，当测点到达孔隙结构的短轴附近，1的应力类型由拉应力变为压应力，最小值出现在短轴位置，当测点再次移动，1的应力类型再次变为拉应力。2、3的变化趋势与1相似，3max为8 MPa，且在短轴位置表现为压应力集中，而2则介于1、3之间。在倾角为45°以及90°椭球状孔隙结构中，主应力在孔隙的短轴附近表现为拉应力集中分布，最大值受周围结构的影响并不一定都存在于短轴点上，往往会出现一定偏移，偏移量最大不会超过45°，而孔隙的尖端位置则呈现出压应力集中分布，这与0°椭球状孔隙中主应力的变化规律不同。

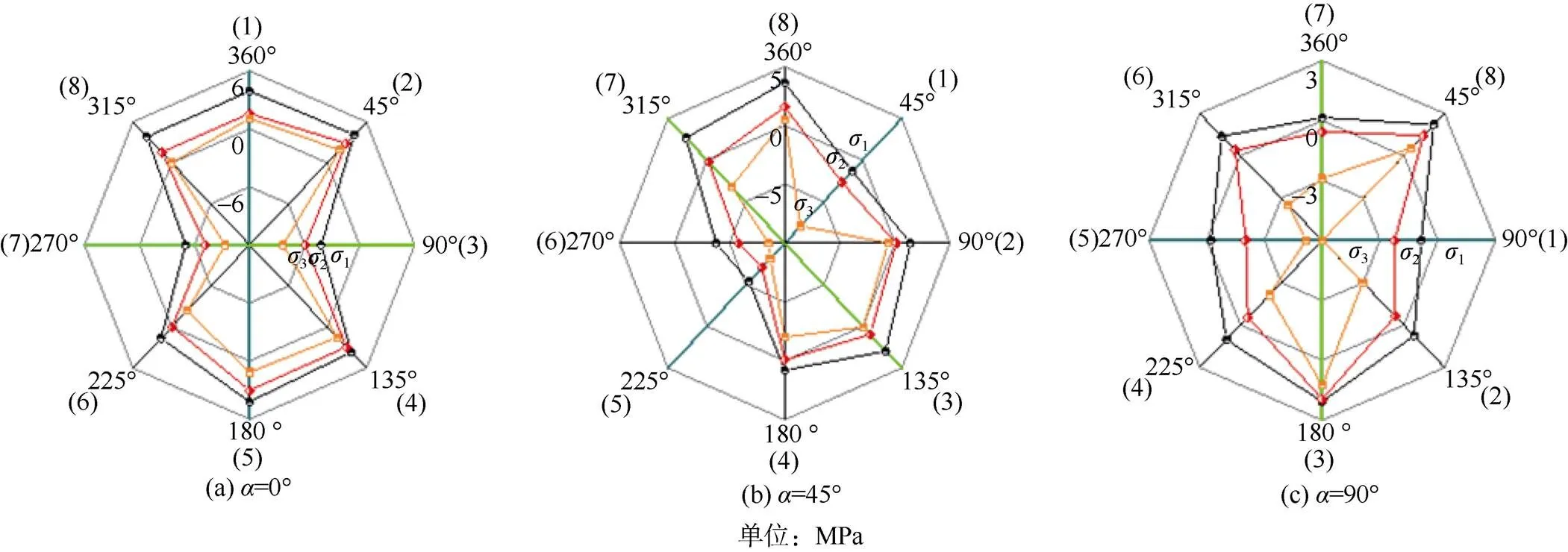
注：(1)—(8)表示不同测点位置。

2.3 理论分析验证

为了验证模拟结果的可靠性，根据球状、椭球状孔隙结构特征以及弹性力学、塑性力学相关定理，构造相应的力学分析模型。

球状孔隙结构周围的主应力情况[19]可表示为：

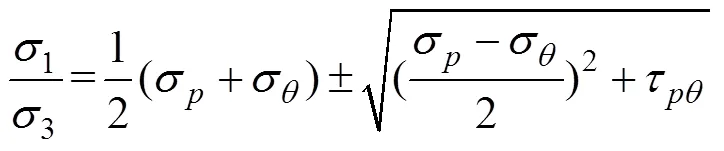
式中：σ为环向正应力；σ为径向正应力，正值为拉应力，负值为压应力；τ为切应力，为球状孔隙上的测点与-面的夹角。

在球状孔隙结构中，其边界条件为=τ=0[20]。由此可得其环向正应力为：

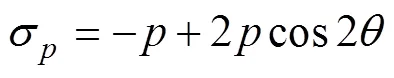
式中：为单轴压缩过程中方向承受的均匀压力，定义其方向受拉为正，受压为负。

对式(3)、式(4)联立可得：

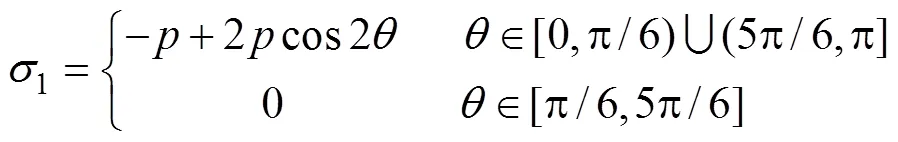
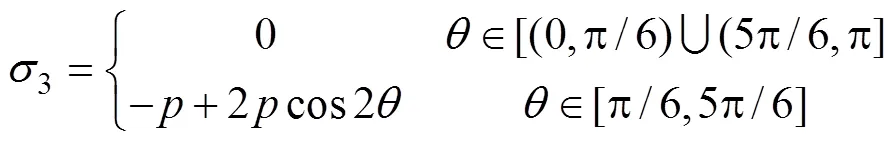
对式(5)、式(6)进行求导计算。当=0或π时，(1)max=；而当=π/2或3π/2时，(3)min=–3。这说明在球状孔隙上下边界会出现拉应力集中，而在其两侧易出现压应力集中。

在椭球状孔隙力学模型中，假设其周围的边界条件为τ=0，任一点的应力分量在曲线坐标系中的表达式[21-22]：

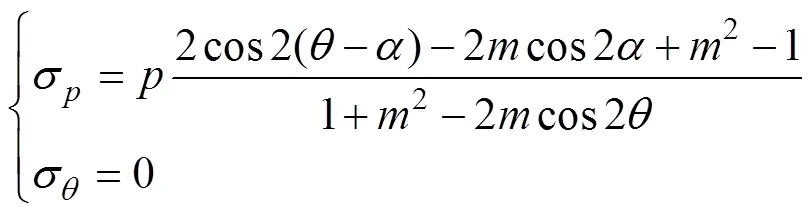
式中：为测点与孔隙长轴的夹角；为与椭圆长短半轴长度有关的几何参数，可表示为=(–)/ (+)，∈[0,1]。

结合式(4)可以看出，1与3的取值情况相似，其值等于σ或0。说明研究椭球状孔隙周围的主应力变化情况相当于探究不同倾角下σ的取值情况。

当=0°时，孔边应力为：

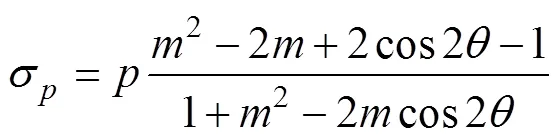
当=π/2或3π/2时，σ取得最小值，(σ)min＜0，即(3)min＜0；当=0或π时，σ取得最大值，(σ)max=，即(1)max=。

当孔隙倾角=90°时，孔边应力为：

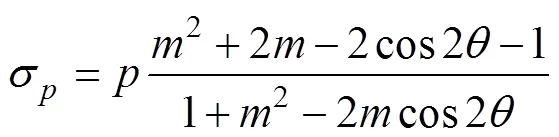
应力情况与0°椭球状孔隙结构的相反。=π/2或3π/2时，σ取得最大值，(σ)max=，即(1)max=；而在=0或π时，σ取得最小值，(σ)min＜0，即(3)min＜0。

当孔隙倾角=45°时，孔边应力为：

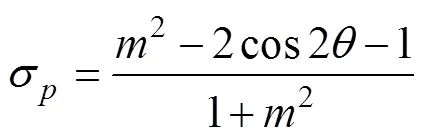
45°与90°椭球状孔隙结构的应力分布类似。

由于=π/2或3π/2对应的是孔隙的短轴位置，而=0、π则对应的是孔隙的尖端位置，将力学模型推导出的结论与模拟获得的结果进行对照，可以看出模拟获得孔隙结构不同位置处的应力类型基本与孔隙力学模型推理出的结论一致。

基于式(8)—式(10)及有限元模拟结果，从理论分析、数值模拟的角度对椭球状孔隙长轴、短轴位置的应力情况做定量研究(表2)。数值模拟得到的压应力与拉应力比值基本处于理论分析结果的范围内。

上述理论分析结果从定性、定量的角度对模拟结果的可靠性进行了验证。由于受到复杂空间位置、测点布置时的误差、孔隙结构力学模型与模拟选取孔隙形状无法完美拟合的影响，模拟获得的孔隙应力值与推导结果没有完全契合，但这并不影响通过应力类型的差异性判断孔隙结构的破坏机理。

表2 椭球状孔隙中上下左右测点σ1、σ3关系

注：0°椭球状孔隙中，1、5测点为拉应力集中，3、7测点为压应力集中；45°及90°椭球状孔隙中，1、5测点为压应力集中，3、7测点为拉应力集中；3(1)表示第3个椭球状孔隙的位置(1)测点，1(3)表示第1个孔隙的位置(3)测点，7(5)表示第7个孔隙的位置(5)测点，5(7)表示第5个孔隙的位置(7)测点。

3 不同加载方式下孔隙结构应力特征

由前面的分析可知，孔隙结构的存在使其周围区域发生应力集中现象，进而导致整个煤岩体结构应力的不均匀分布。因此，孔隙结构应力分布研究对揭示煤岩体物理力学性质至关重要。除形状和角度外，加载方式也是影响孔隙周围应力分布的重要因素。进一步从球状孔隙入手，对不同加载方式下孔隙周围的应力分布规律展开研究。

3.1 轴向加载

首先，在煤岩体模型左侧重新选取3个球状孔隙(A7—A9)，布置4个测点按照模拟方案1测取不同轴向加载速度下球状结构周围的Mises应力峰值以及1最大值、最小值应力情况，结果见表3。其中，1、2、3、4号测点分别对应孔隙的上、右、下、左4个区域，如图5所示。

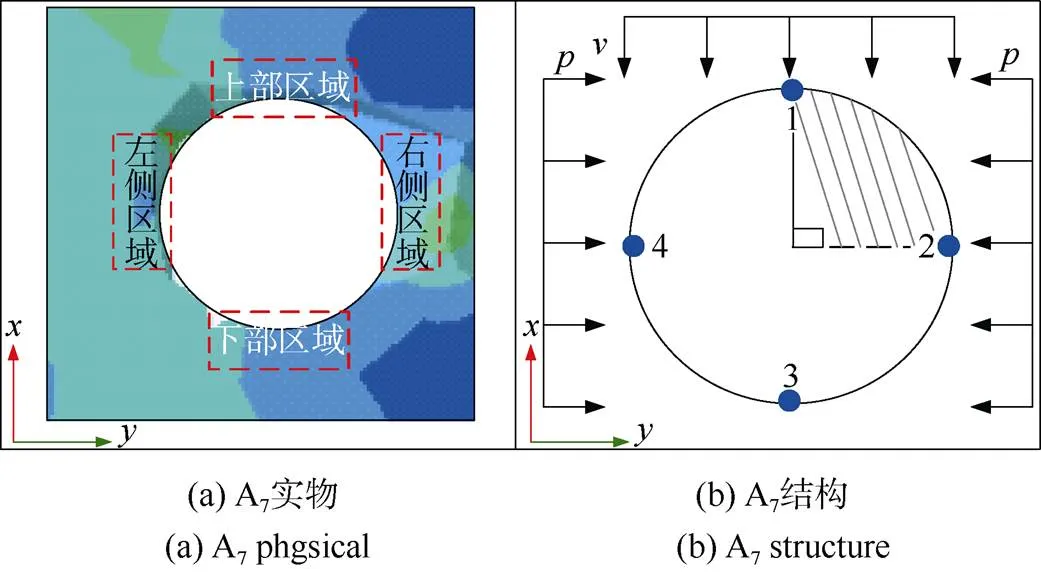
图5 球状孔隙结构截面

通过对比1值可以发现，不同加载速度下球状孔隙左右区域仍然表现为压应力集中，上部区域表现为拉应力集中，下部区域内1的变化情况较为复杂，并不完全表现为压应力集中。这与球状孔隙A1—A6的情况相似。而Mises应力与1具有不同的变化趋势。随着轴向加载速度的增加，上下区域测点的Mises应力峰值逐渐增大，而左右两侧区域测点的Mises应力峰值则逐渐减小。对于1而言，上下、左右区域的1最大值基本随着轴向加载速度的增加而逐渐增大，只有在A9孔隙左右区域出现了少量特殊变化；而最小值变化较为复杂，变化规律趋于多元化。王学滨[23]通过对宏观岩样变形特征影响因素的研究，发现单轴压缩过程中轴向应力峰值(1应力最大值)会随着加载速度的增加而增加。这与本文模拟得到的孔隙结构1应力变化规律具有一定的相似性。由此可以看出，轴向加载速度通过改变轴向应力值进而影响宏观、微观煤岩体结构的变形[24-26]。

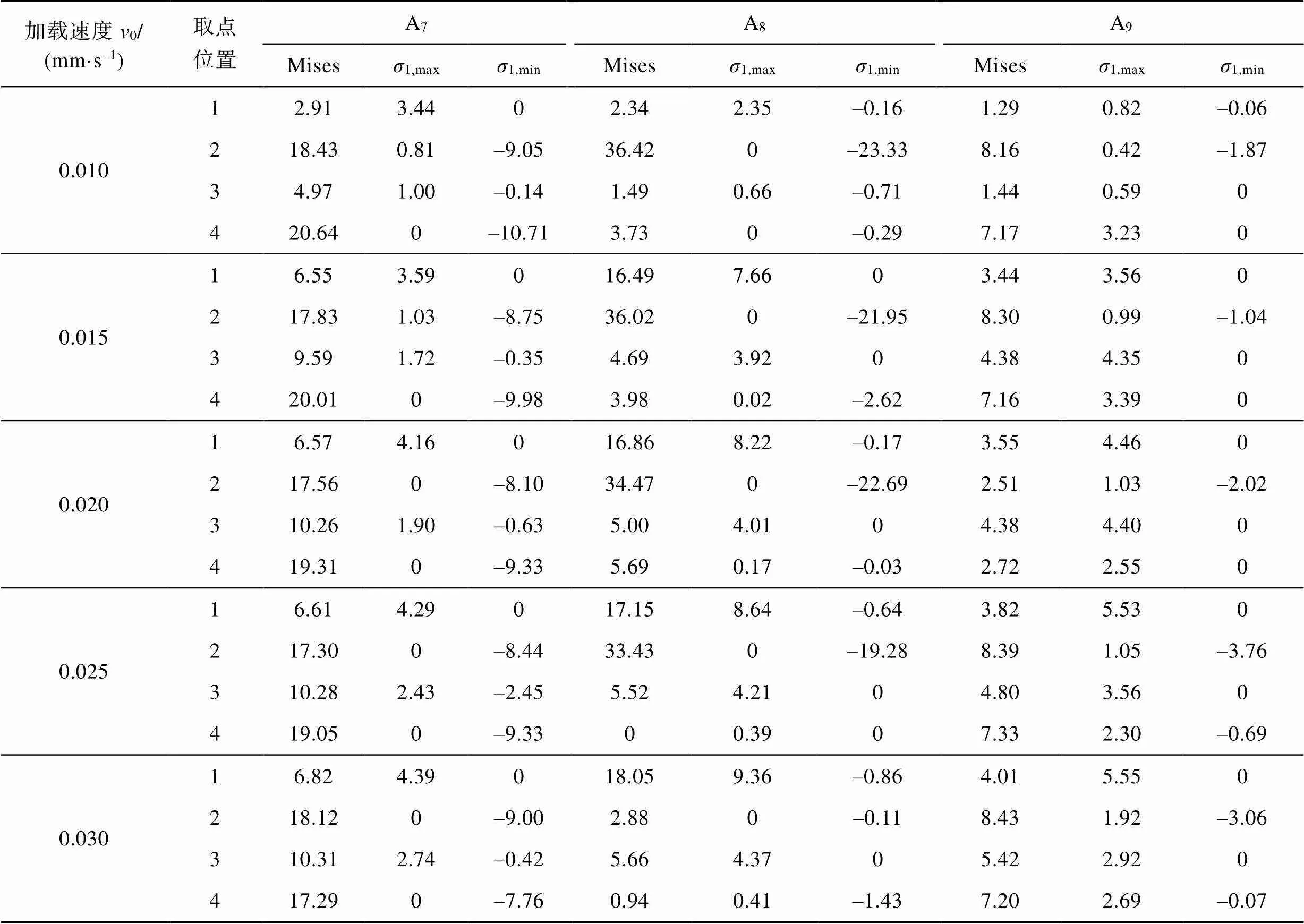
表3 A7—A9球状孔隙周围测点的主应力情况

3.2 围压作用

为了获取围压作用下孔隙结构的应力变化特征，提取模拟数据并绘制A7—A9孔隙结构“应力–时间”“应力–应变”的变化曲线，如图6所示。对比孔隙结构应力随时间的变化曲线，可以看出：在加载之初，1应力出现短暂的弯曲上升，此过程中围压对其产生的影响较小，因此，3条不同围压曲线重合度较高；随着时间的增加，1应力线性增大，表现出明显的线弹性变化特征，此时，围压产生的影响依然较小；而当1应力逐渐到达最大值时，曲线发生差异性变化，围压造成的影响显现，其基本变化规律为“围压越高，1应力最大值越大”；随着时间的继续增加，1应力处于波动下降阶段，围压对于1应力变化的影响依然存在。

图6d—图6f反映了3种孔隙结构的应力–应变变化关系，从图中不难看出围压作用下微细观孔隙结构依然经历了压密、弹性、塑性和破坏4个阶段。但是模拟获得的压密阶段特征不明显，这主要是由于所研究的模型尺寸较小，内部含有的原始裂纹数量较少，加之受力后孔隙结构的迅速闭合，影响了微细观煤岩体结构的压密过程，从而减弱了局部孔隙结构的压密形变。随着模拟进一步向塑性变形阶段发展，围压作用效果显现，应力值会随着围压的逐渐升高而增大，这与“应力–时间”变化曲线反映出的现象相似。

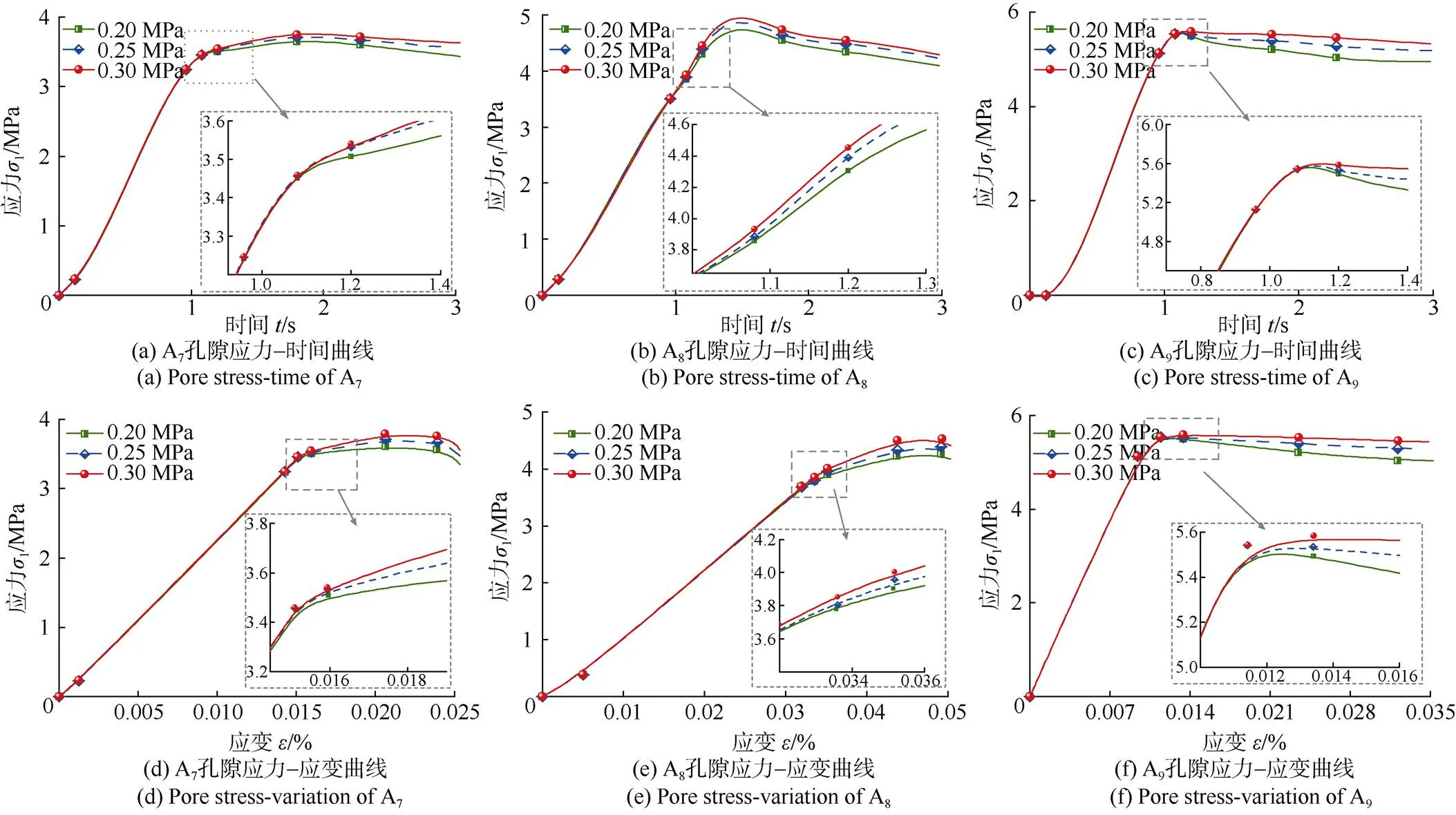
图6 围压作用下A7—A9孔隙区域应力变化情况

对比3种孔隙结构的峰值强度可以发现，虽然孔隙结构形状类似，但是其峰值强度却不尽相同(A7峰值强度为3.78 MPa，A8峰值强度为4.53 MPa，A9峰值强度为5.58 MPa)，这可能是由于选取的孔隙周围结构的差异性影响了该区域内的结构强度，同时也引起了应力的不均匀分布，在上述因素的综合作用下造成了3种孔隙结构峰值强度的不同。当模型到达破坏阶段时，应力–应变曲线呈下降趋势，所反映出的残余强度会随着围压的增加而逐渐增大，这表明围压越低煤岩体孔隙结构的脆性破坏越明显[27]。

4 结论

a. 在单轴压缩过程中，孔隙周围出现了明显的应力集中现象。球状孔隙结构不同区域的应力集中类型不同，上下区域易出现拉应力集中分布，左右两侧区域则更多表现为压应力集中分布。随着椭球状孔隙结构倾角在0~90°变化，其长轴区域由拉应力集中变为压应力集中，短轴区域则由压应力集中变为拉应力集中。

b.随着轴向加载速度的增加，球状孔隙上下区域的Mises应力峰值逐渐增大，而左右两侧区域的Mises应力峰值逐渐减小。1的最大值基本随着轴向加载速度的增加而逐渐增大，但其最小值变化较为复杂。

c. 围压的变化没有改变球状孔隙结构的“应力–应变”趋势，其依然经历了压密、弹性、塑性和破坏4个阶段。较低的围压条件造成弹性阶段曲线高度重合。通过模拟残余强度与围压之间的变化关系可以看出，围压越低煤岩体孔隙结构的脆性破坏越明显。

d. 采用CT三维重建与数值模拟相结合方法探究煤岩体孔隙周围的应力变化特征，丰富了煤岩体力学性质的研究途径，在保证实验精度的同时避免了宏观煤岩体加载实验操作的复杂性，实现了加载过程的可视化。但模拟并未涉及煤岩体孔隙的数量、复杂的空间位置对应力分布影响的研究，有待后续重点研究。

[1] LIU Qiang，NIE Wen，HUA Yun，et al. Research on tunnel ventilation systems: dust diffusion and pollution behaviour by air curtains based on CFD technology and field measurement[J]. Building and Environment，2019，147：444–460.

[2] ALEXEEV A D，REVVA V N，ALYSHEV N A，et al. True triaxial loading apparatus and its application to coal outburst prediction[J]. International Journal of Coal Geology，2004，58(4)：245–250.

[3] SUN Huan，LIU Xiaoli，ZHU J. B. Correlational fractal characterisation of stress and acoustic emission during coal and rock failure under multilevel dynamic loading[J]. International Journal of Rock Mechanics and Mining Sciences，2019，117：1–10.

[4] LIU Shumin，LI Xuelong，LI Zhonghui，et al. Energy distribution and fractal characterization of Acoustic Emission(AE) during coal deformation and fracturing[J]. Measurement，2019，136：122–131.

[5] ZHAO Jun，FENG Xiating，ZHANG Xiwei，et al. Brittle and ductile creep behavior of Jinping marble under true triaxial stress[J]. Engineering Geology，2019，258：105157.

[6] 屈丽娜，李波. 基于西原加速模型的煤体蠕变特性试验[J]. 煤田地质与勘探，2019，47(6)：115–120. QU Lina，LI Bo. Nishihara acceleration model-based experiment of creep characteristics of coal[J]. Coal Geology & Exploration，2019，47(6)：115–120.

[7] RENNER J，EVANS B，SIDDIQI G. Dislocation creep of calcite aggregates[J]. Journal of Geophysical Research：Solid Earth，2002，107(B12).

[8] 余杰，刘晓辉，郝齐钧. 不同围压下煤岩声发射基本特性及损伤演化[J]. 煤田地质与勘探，2020，48(3)：128–136. YU Jie，LIU Xiaohui，HAO Qijun. Acoustic emission characteristics and damage evolution of coal-rock under different confining pressures[J]. Coal Geology & Exploration，2020，48(3)：128–136.

[9] WU Mengmeng，WANG Jianfeng. Reassembling fractured sand particles using fracture-region matching algorithm[J]. Powder Technology，2018，338：55–66.

[10] XU Hong，FENG Xiating，YANG Chengxiang，et al. Influence of initial stresses and unloading rates on the deformation and failure mechanism of Jinping marble under true triaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences，2019，117：90–104.

[11] YANG Xinxiang，KURU E，GINGRAS M，et al. CT-CFD integrated investigation into porosity and permeability of neat early-age well cement at downhole condition[J]. Construction and Building Materials，2019，205：73–86.

[12] DURR N，SAUER M，HIERMAIER S. A numerical study on mesoscale simulation of quartzite and sandstone under shock loading[J]. International Journal of Impact Engineering，2017，108：73–88.

[13] ZHANG Shihuai，WU Shunchuan，DUAN Kang. Study on the deformation and strength characteristics of hard rock under true triaxial stress state using bonded-particle model[J]. Computers and Geotechnics，2019，112：1–16.

[14] SUN Wei，HOU Kepeng，YANG Zhiquan，et al. X-ray CT three-dimensional reconstruction and discrete element analysis of the cement paste backfill pore structure under uniaxial compression[J]. Construction and Building Materials，2017，138：69–78.

[15] 丁鑫，肖晓春，吴迪，等. 不同加载路径煤岩破裂过程声-电荷复合信号特性[J]. 煤炭学报，2016，41(增刊2)：359–368. DING Xin，XIAO Xiaochun，WU Di，et al. Study on compound signal characteristics of acoustic emission and charge induction in coal rock failure under different loading paths[J]. Journal of China Coal Society，2016，41(Sup.2)：359–368.

[16] ZHAO Yixin，SONG Honghua，LIU Shimin，et al. Mechanical anisotropy of coal with considerations of realistic microstructures and external loading directions[J]. International Journal of Rock Mechanics and Mining Sciences，2019，116：111–121.

[17] SUN Huafei，YANG Yongming，JU Yang，et al. Numerical analysis of deformation，failure and energy release mechanisms of fractured coal rock under unloading conditions[J]. Journal of China Coal Society，2014，39(2)：258–272.

[18] PENG Jun，WONG L N Y，THE C I. A re-examination of slenderness ratio effect on rock strength：Insights from DEM grain-based modelling[J]. Engineering Geology，2018，246：245–254.

[19] 孙华飞，杨永明，鞠杨，等. 开挖卸荷条件下煤岩变形破坏与能量释放的数值分析[J]. 煤炭学报，2014，39(2)：258–272. SUN Huafei，YANG Yongming，JU Yang，et al. Numerical analysis of deformation，failure and energy release mechanisms of fractured coal rock under unloading conditions[J]. Journal of China Coal Society，2014，39(2)：258–272.

[20] 刘京红，姜耀东，赵毅鑫，等. 煤岩破裂过程CT图像的分形描述[J]. 北京理工大学学报，2012，32(12)：1219–1222. LIU Jinghong，JIANG Yaodong，ZHAO Yixin，et al. Fractal description of coal damage process based on CT image[J]. Transactions of Beijing Institute of Technology，2012，32(12)：1219–1222.

[21] 王会杰. 深部裂隙煤岩渗流性质的试验研究[D]. 北京：中国矿业大学(北京)，2013. WANG Huijie. Experimental study of fluid seepage in fractured coal under simulated deep coal mining[D]. Beijing：China University of Mining and Technology(Beijing)，2013.

[22] 王刚，杨鑫祥，张孝强，等. 基于CT三维重建与逆向工程技术的煤体数字模型的建立[J]. 岩土力学，2015，36(11)：3322–3328. WANG Gang，YANG Xinxiang，ZHANG Xiaoqiang，et al. Establishment of digital coal model using computed tomography based on reverse engineering technology and three-dimensional reconstruction[J]. Rock and Soil Mechanics，2015，36(11)：3322–3328.

[23] 王学滨. 加载速度对断层–围岩系统变形及快速回跳的影响[J]. 岩土力学，2006，27(2)：242–246. WANG Xuebin. Numerical simulation of influence of loading rate on deformation characteristics and snap-back for fault band and elastic rock system[J]. Rock and Soil Mechanics，2006，27(2)：242–246.

[24] 何俊，潘结南，王安虎. 三轴循环加卸载作用下煤样的声发射特征[J]. 煤炭学报，2014，39(1)：84–90. HE Jun，PAN Jienan，WEANG Anhu. Acoustic emission characteristics of coal specimen under triaxial cyclic loading and unloading[J]. Journal of China Coal Society，2014，39(1)：84–90.

[25] FENG Junjun，WANG Enyuan，CHEN Xia，et al. Energy dissipation rate：An indicator of coal deformation and failure under static and dynamic compressive loads[J]. International Journal of Mining Science and Technology，2018，28(3)：397–406.

[26] 彭瑞东，鞠杨，高峰，等. 三轴循环加卸载下煤岩损伤的能量机制分析[J]. 煤炭学报，2014，39(2)：245–252.PENG Ruidong，JU Yang，GAO Feng，et al. Energy analysis on damage of coal under cyclical triaxial loading and unloading conditions[J]. Journal of China Coal Society，2014，39(2)：245–252.

[27] ZHAO Gaofeng，RUSSELL A R，ZHAO Xiaobao，et al. Strain rate dependency of uniaxial tensile strength in Gosford sandstone by the distinct lattice spring model with X-ray micro CT[J]. International Journal of Solids and Structures，2014，51(7/8)：1587–1600.

Numerical simulation of pore structure stress characteristics of coal and rock mass

WANG Gang1,2, JIANG Chenghao2, CHEN Xuechang2

(1. Mining Disaster Prevention and Control-Ministry of State Key Laboratory Breeding Base, Shandong University of Science and Technology, Qingdao 266590, China; 2. College of Safety and Environmental Engineering, Shandong University of Science and Technology, Qingdao 266590, China)

In order to explore the stress distribution around the pores of coal and rock mass under different loading modes, the skeleton model of coal and rock mass with different pore shapes was constructed through CT three-dimensional reconstruction technology, and uniaxial and triaxial compression experiment simulations were conducted using ABAQUS software. The results showed that under uniaxial compression, the upper and lower regions of spherical pores showed tensile stress concentration, while the left and right regions showed compressive stress concentration.The stress concentration types in the long and short axis of elliptic pores were distinct with different dip angles.Under uniaxial compression, axial loading velocity affected the maximum values of Mises stress and1stress around spherical pores. In the process of triaxial compression, the pore structure still went through four stages of compaction, elasticity, plasticity and failure. The lower confining pressure made the “stress-strain” curve and “stress-time” curve highly coincide in the elastic stage.This study provides a new method for the study of coal and rock mechanics from the microscopic point of view.

CT three-dimensional reconstruction; pore structure; numerical simulation; uniaxial compression; three axis compression

移动阅读

语音讲解

TD712

A

1001-1986(2021)01-0057-08

2020-10-25；

2020-12-28

国家自然科学基金项目(51674158，51974176)；山东省高等学校青创科技支持计划项目(2019KJH006)；山东省自然科学杰出青年基金项目(ZR2020JQ22)

王刚，1984年生，男，山东临沂人，博士，教授，从事煤矿灾害预测与防治研究. E-mail：gang.wang@sdust.edu.cn

王刚，江成浩，陈雪畅.煤岩体孔隙结构应力特征的数值模拟研究[J]. 煤田地质与勘探，2021，49(1)：57–64. doi：10.3969/j.issn.1001-1986.2021.01.006

WANG Gang，JIANG Chenghao，CHEN Xuechang. Numerical simulation of pore structure stress characteristics of coal and rock mass[J]. Coal Geology & Exploration，2021，49(1)：57–64. doi: 10.3969/j.issn.1001-1986.2021.01.006

(责任编辑 范章群)