关于一道高考题的两种解法

内蒙古阿拉善盟第一中学 王嘉琦

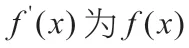
解法一（分离参数法）

当x=0 时，f（0）≥0 成立；

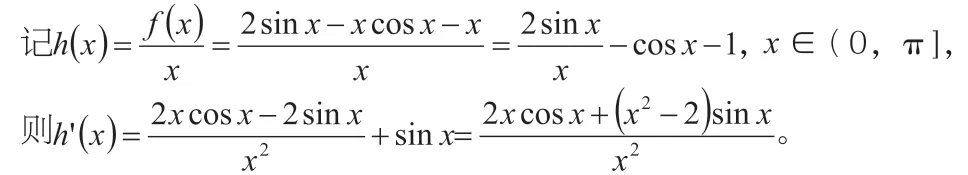
记m（x）=2xcosx+（x2-2）sinx，

则m'（x）=2cosx-2xsinx+2xsinx+（x2-2）cosx=x2cosx。

x π+0-↑极大值 ↓ 0

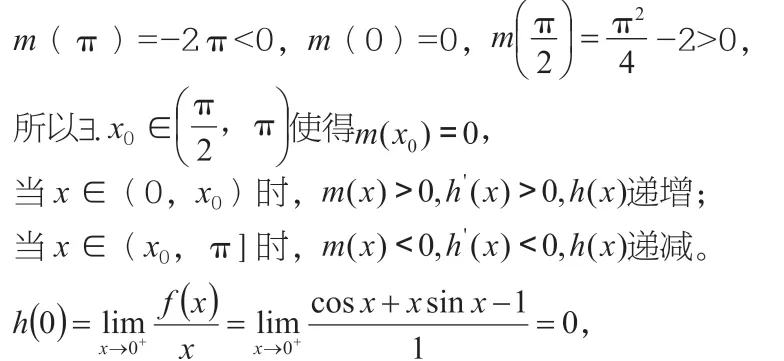
因此a 的取值范围是(-∞，0]。

点评：分离参数法相对易于想到，但是学生在具体的解答过程中，对新设函数求导不容易做对。

解法二（分类讨论法）

x ∈（0，π]时，f（x）≥ax 成立，

即f（x）-ax ≥0 成立。

记h（x）=f（x）-ax，则只需h（x）min≥0，

则h'（x）=f '（x）-a=cosx+xsinx-1-a。

记r（x）=cosx+xsinx-1-a，则r'（x）=xcosx。

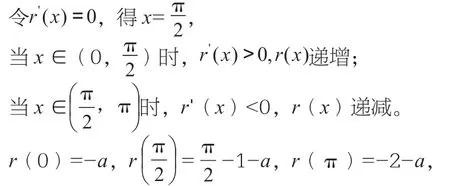
所以h（x）在[0，2π]上递减，

所以x ∈[0，x1）∪（x1，π]时，r（x）＜0，

x ∈（x1，x2）时，r（x）＞0。

所以x ∈（0，x0）时，r（x）＞0，h'（x）＞0，h（x）递增，

x ∈（x0，π]时，r（x）＜0，h'（x）＜0，h（x）递减，

h（0）=0，h（π）=-aπ ≥0 成立。

当a ≤-2 时，r（x）≥0，h'（x）≥0，h（x）递增，

h（x）min=h（0）=0 成立。

因此a 的取值范围是（-∞，0]。

点评：分类讨论法对于学生而言是有一定难度的，但是部分不追求高分的孩子可以尝试用这种方法，一般得分会相对高一些。