基于多目标优化的乘用车后排座椅轻量化设计

黄胜超,廖耀青,单志颖,李建阳,李旭亮

(1.浙江天成自控股份有限公司技术研发中心,浙江台州 318000；2.温州大学机电工程学院，浙江温州 325035)

0 引言

目前，安全、节能和环保三大主题制约着汽车工业的发展，而轻量化作为实现这些目标的重要手段已经成为国内外研究的热点。其中，在汽车安全性和轻量化的研究中后排座椅往往被忽略。因此，在满足安全法规和乘坐舒适性的同时，减轻汽车后排座椅的质量对于汽车行业的发展具有重大意义[1]。近年来，利用轻量化的汽车材料、对部件结构进行优化设计和采用新的制造工艺是解决汽车轻量化问题的3个重要方面[2]。例如，曹立波等[3]结合静态和动态拓扑优化方法对汽车前纵梁进行耐撞性设计，进而获得前纵梁最大吸能时的结构形式。白煜和丁晓红[4]以及ZHANG等[5]采用拓扑优化技术在满足汽车座椅安全性能的前提下对乘用车座椅靠背结构进行轻量化设计。现有对汽车座椅的轻量化设计研究大多集中在结构优化上，具有一定的局限性。很少有研究将汽车座椅骨架独立部件的厚度和材料同时作为设计变量，并根据每个结构部件的预期功能为其寻找厚度和材料的最佳组合。因此，文中采用结构-材料一体化的优化方法对汽车座椅进行轻量化设计。

汽车座椅结构是一个复杂的工程系统，在对其进行轻量化设计时需要考虑多学科的影响，包括安全性和结构强度、刚度等。同时，汽车座椅的碰撞分析模型较为复杂，优化过程中会带来庞大的计算量和计算成本。相比之下，采用响应面法(RSM)、克里金插值方法(Kriging)和径向基神经网络方法(RBF)等建立近似模型进行多目标优化具有效率高和容易弥合多学科优化之间的差距等优点。例如，白俊峰等[6]利用响应面法构建了胫骨加速度峰值和膝关节弯曲角度等的近似模型，并将其运用到汽车保险杠的材料匹配中。柴灏等[7]建立基于响应面法的多材料、多目标优化模型，利用NSGA-Ⅱ算法对优化问题进行求解，在提升一阶模态的同时，实现了汽车座椅骨架的轻量化设计。然而，由于汽车座椅轻量化设计过程中需要考虑许多相互冲突的指标(质量、位移、应变等)，通常单一的近似模型方法无法对所有指标同时构建高精度的近似模型。因此，文中采用3种常用的近似模型方法对所有评价指标进行拟合构建近似模型。通过对比分析各个指标的不同近似模型拟合精度，最终采用RSM-RBF混合近似模型方法进行汽车座椅的结构-材料一体化多目标轻量化设计。

多目标优化问题的特征之一是存在多组非支配解以便设计人员进行选择，然而根据主观意识和工程经验来选择一个特定的解具有一定的随机性[8]。为了解决上述问题，许多国内外研究者采用TOPSIS和灰色关联度(GRG)等方法对非支配解集进行筛选排序，获得最佳折中解。WANG等[9]在对客车副车架进行轻量化设计中，利用熵权理论和TOPSIS方法对所有解进行排序进而得到最佳折中解。蒋荣超等[10]为提高汽车行驶平顺性和操纵稳定性等整车动力学性能优化匹配效率，提出基于熵权法和TOPSIS方法的结构综合贡献系数计算方法，以此筛选出对悬架性能影响较大的结构参数作为设计变量。因此，采用基于熵权TOPSIS方法对多目标优化得到的非支配解集进行综合性能排序，选取汽车座椅多目标轻量化设计中的折中解，具有重要的工程实用价值。

鉴此，本文作者以某乘用车后排座椅作为研究对象，结合有限元理论建立仿真模型，并通过行李箱碰撞试验验证仿真模型的正确性。基于行李箱碰撞试验，采用NSGA-II算法结合RSM-RBF混合近似模型和基于熵权TOPSIS方法对座椅进行结构-材料一体化多目标轻量化设计研究。结果表明，所提出的轻量化设计方法可以将零件材料和厚度合理地分配到座椅骨架结构中，为汽车座椅轻量化设计提供理论指导。

1 建模与验证

1.1 有限元模型的建立

文中依据“安全基础上的轻量化设计”理论，采用数值模拟结合优化算法对某乘用车后排座椅进行轻量化设计。按照《GB15083—2006 汽车座椅系统强度要求及试验方法》，基于HyperMesh软件建立行李箱碰撞试验有限元模型如图1所示。

图1 行李箱碰撞试验有限元模型

1.2 有限元模型的验证

为了确保仿真计算结果的可靠性和准确性，对建立好的行李箱碰撞试验有限元模型进行仿真分析，并和实际试验结果(图2)进行对比验证。对比结果如图3所示，结果表明：仿真计算结果与试验结果的位移曲线趋势和幅度有较好的一致性，且绝对误差也相差不大，因此可以判断文中建立的有限元模型具有良好的精度，可用于后续的多目标优化设计研究。

图2 行李箱碰撞实验

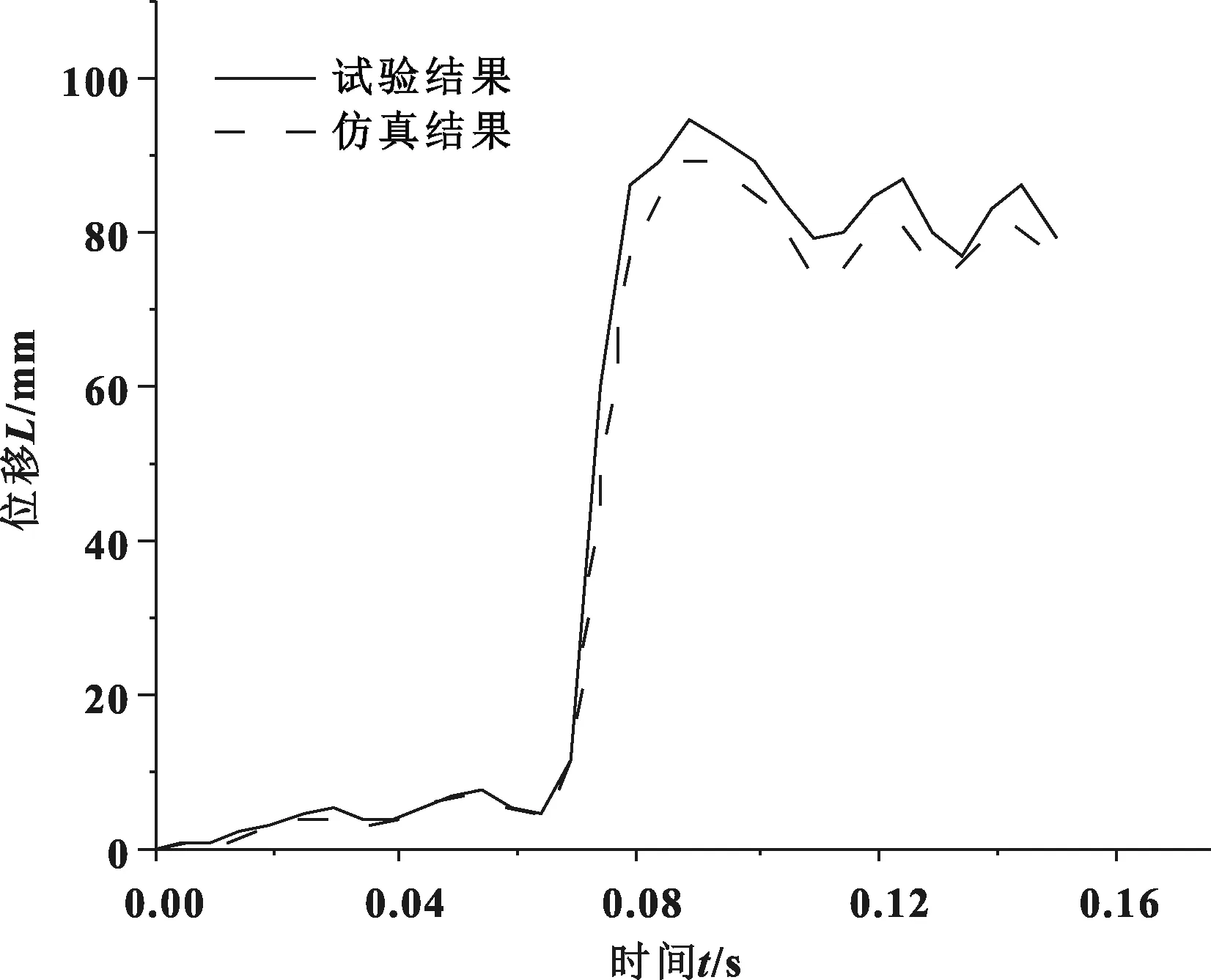
图3 行李箱碰撞仿真和实际试验中头枕位移曲线结果对比

2 优化设计分析

2.1 评价指标和设计变量

后排座椅行李箱碰撞过程是一种非常复杂的非线性动态过程，可作为安全性能的评价指标也是多样的，如速度、位移和变形量等。根据法规要求，试验过程中头枕的前轮廓不允许移出座椅设计基准点(R点)前方的150 mm横向垂面，同时这里允许靠背骨架及其紧固件有一定程度的变形，但不能失效。文中采用最大应变准则作为失效准则，同时引入应变指数来评判零部件是否失效如式(1)所示。当应变指数大于1时表示该部件此时处于失效状态，反之则处于安全状态。因此，将头枕最大位移量、各优化部件应变指数及其总质量作为安全性能和轻量化的评价指标。

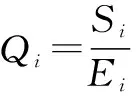
(1)

式中:Qi为第i个部件的应变指数；Si为第i个部件的塑性应变；Ei为第i个部件所使用材料的延伸率。

在后排座椅行李箱碰撞过程中，主要的受力和吸能部件为靠背骨架，因此文中将座椅靠背骨架所有管件与板件的厚度和材料作为设计变量。同时，根据座椅靠背骨架结构的对称性和功能性，将其简化为12个变量，优化部件分布如图4所示。根据工程经验和优化部件的吸能曲线(图5)对优化部件设定厚度和材料的优化取值范围。表1为优化设计备选材料性能参数，根据该表材料的力学性能分为三组，每组4个备选材料；表2为优化部件的设计变量及其取值范围。

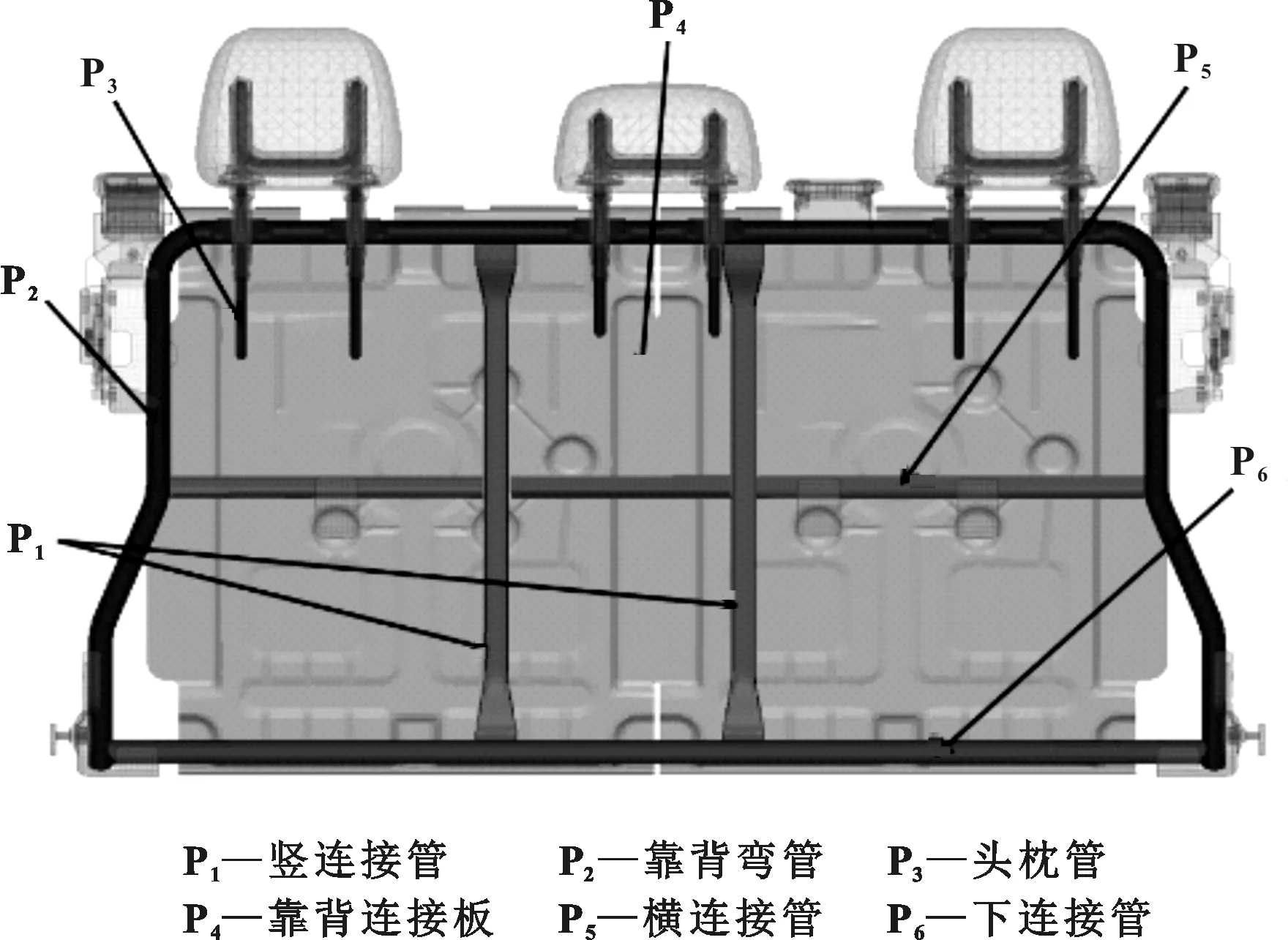
图4 优化部件分布情况

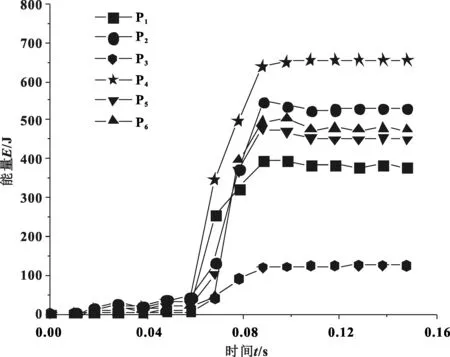
图5 优化部件吸能曲线

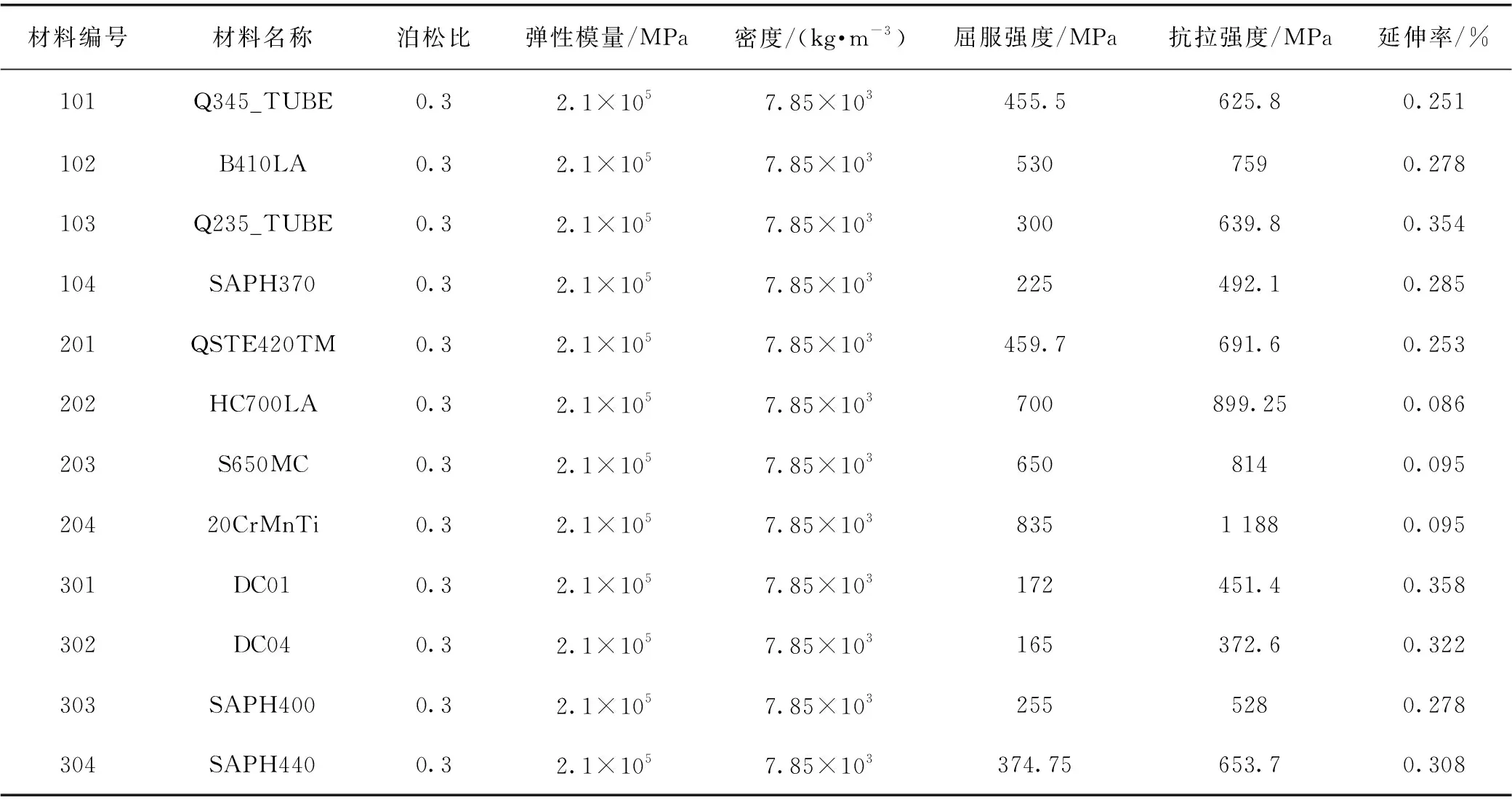
表1 优化设计备选材料

表2 试验参数及取值范围

2.2 建立样本库

优化拉丁超立方试验设计方法是一种分层随机抽样，通过最大化地使每一个边缘分布分层，保证每一个变量范围的全覆盖，然后从变量的分布区间进行高效采样，具有非常好的空间填充性和均衡性[11]。根据优化拉丁超立方采样标准[12]如式(2)所示，文中共有12个设计变量，最少应采样91个，为保证后续建立的近似模型有较好的拟合精度，故抽取200组样本。

(2)

式中:m为最小采样数，n为设计变量数。

根据样本数据，对原始行李箱碰撞试验有限元模型进行参数修改并提交计算，通过后处理提取座椅优化部件总质量M、头枕最大位移量L和6个优化部件P1—P6对应的应变指数Q1～Q6共8个响应，部分试验布局及结果见表3。

表3 试验布局及结果

2.3 混合近似模型的建立

为了选择合适的近似模型来精确逼近响应值，文中采用3种常用的近似模型，分别为RSM、Kriging和RBF，在选定的设计变量和所有响应值之间构建近似模型。然后，在拟合精度比较的基础上，针对不同的响应值采用不同的近似模型方法，以便同时逼近所有响应值。

为了评估近似模型的拟合精度，文中采用以下4个最有效的评估指标[13]：

(3)

(4)

(5)

(6)

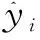
从公式定义中可以看出，R2的值越大，emax、eavg和eRMS的值越小，响应值在设计空间中的拟合精度就越高。

从第2.2节得到的200组样本中随机抽取185组作为训练样本集进行近似模型的建立，然后利用剩余的15组样本数据进行误差分析。根据图6(编号1—8分别代表M、L、Q1、Q2、Q3、Q4、Q5、Q6)3种近似模型的精度评估系数比较可以总结出以下结论：

(1)在样本数量足够的情况下，对于优化部件总质量M这种非线性程度较低的问题，3种近似模型均具有较高的精度；而头枕最大位移量L和优化部件应变指数Q1～Q6的非线性程度较高，近似模型的拟合精度相对较低。

(2)优化部件总质量M、头枕最大位移量L和应变指数Q1、Q2使用RSM方法拟合时与另外两种近似模型相比拟合精度评估系数中R2的值更大，emax、eavg和eRMS的值更小；而应变指数Q3～Q6采用RBF方法拟合时具有相同的效果。

因此，文中最终采用RSM-RBF混合近似模型方法建立设计变量和响应值之间的复杂映射关系。优化部件总质量M、头枕最大位移量L和应变指数Q1、Q2采用RSM方法，应变指数Q3～Q6使用RBF方法来构建混合近似模型。通过这种混合近似模型，除了应变指数Q6的精度评估系数R2为0.765偏低一点外，其余响应值的精度评估系数R2均在0.85以上。同时其他精度评估系数emax、eavg和eRMS均在0.267以下，表明采用RSM-RBF混合近似模型可以获得较好的拟合精度，可用于后续的多目标优化设计,比较结果如图6所示。

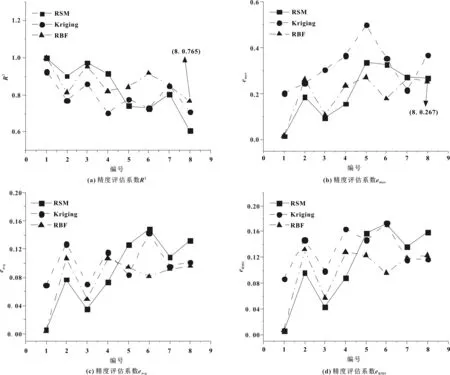
图6 不同近似模型的精度评估系数比较

2.4 多目标优化数学模型

文中以座椅靠背骨架结构的厚度和材料作为设计变量，优化部件总质量和头枕最大位移量最小化作为优化目标，优化部件应变指数作为约束。考虑到有限元模型仿真模拟与实际试验有轻微误差，且零部件需要一定的安全系数，文中将优化部件的应变指数约束到0.8以下,得到的多目标优化数学模型如下所示：

(7)

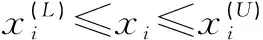
3 优化结果分析与验证

3.1 优化结果

针对上述多目标优化问题，文中在Isight软件中基于第2.3节建立的RSM-RBF混合近似模型，对优化目标设定权重后采用NSGA-Ⅱ算法进行寻优。对应的优化算法参数设置见表4，优化部件总质量和头枕最大位移量的权重根据样本数据采用式(8)所示的熵权法[14]求得，分别为0.588和0.412。最后经过18 001次迭代，获得979个Pareto解，其中包括一个Isight推荐最优方案A。

(8)

式中:xij(i=1,2,…,n;j=1,2,…,m)为第i个样本的第j个目标，n为样本个数，m为目标个数；Ej为第j个目标的信息熵；Wj为第j个目标的权重。

表4 NSGA-Ⅱ的优化参数设置

由图7所示的NSGA-Ⅱ优化结果可知，寻优后的Pareto解集集中在一条细窄的曲线上，说明NSGA-Ⅱ算法的优化结果综合性能良好。

图7 NSGA-Ⅱ优化结果

3.2 基于熵权TOPSIS方法排序

TOPSIS方法基本过程为基于归一化后的原始数据矩阵，采用余弦法找出有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。具体执行过程[15]如下：

(1)构造归一化初始矩阵

将NSGA-Ⅱ算法寻优得到的Pareto解作为决策矩阵，可表示为：

(9)

将定义的决策矩阵进行归一化处理，计算公式为：

(10)

式中：xij(i=1,2,…,n;j=1,2,…,m)为第i个Pareto解的第j个目标，n为样本个数，m为目标个数；Zij为xij归一化处理后的结果。

(2)确定最优方案和最劣方案

文中的目标均为极小型指标，最优方案Z+由Z中每列元素的最小值构成,最劣方案Z-由Z中每列元素的最大值构成：

(11)

(3)确定权重

优化部件总质量和头枕最大位移量的权重根据Pareto解集采用式(8)所示的熵权法求得，分别为0.748和0.252。

(4)计算Pareto解与最优和最劣方案的

(12)

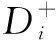
(5)计算Pareto解与最优方案的接近程度Ci

(13)

当Ci越接近1时，说明该组Pareto解越优。

由于979组Pareto最优解集中在一条细窄的曲线上，存在大量重叠解。故文中将最优解按优化部件总质量的大小进行排序，每隔20组取1组数据，共获得48组Pareto最优解，然后采用基于熵权TOPSIS方法对其进行排序。图8展示了48组Pareto最优解与最优方案的接近程度，其中第27个方案(TOPSIS方法推荐方案B)获得了最大的接近程度0.864。表5展示了汽车座椅各优化方案与优化前的评价指标对比情况和近似模型与仿真模型之间的误差情况。从轻量化和安全性能两个方面来看，优化方案A对优化部件质量和头枕位移量都有较大的改善，除了横连接管的应变指数Q5达到0.779以外，其他优化部件的应变指数均在0.5以下。相比较于方案A，优化方案B在轻量化方面较好，质量减少3.57 kg，相对减少率约为整椅的16.73%。同时，各优化部件的应变指数均在0.6以下，说明各优化部件的应变都不大，具有较好的安全性能。近似模型与仿真模型最大误差率为11.6%，因此近似模型能够满足精度要求。综上分析，优化方案B具有较好的综合性能，安全性能指标呈现不均匀和不成比例的变化，但都处于安全状态。在保证了汽车座椅安全性能的前提下，大幅度地减轻了座椅质量。

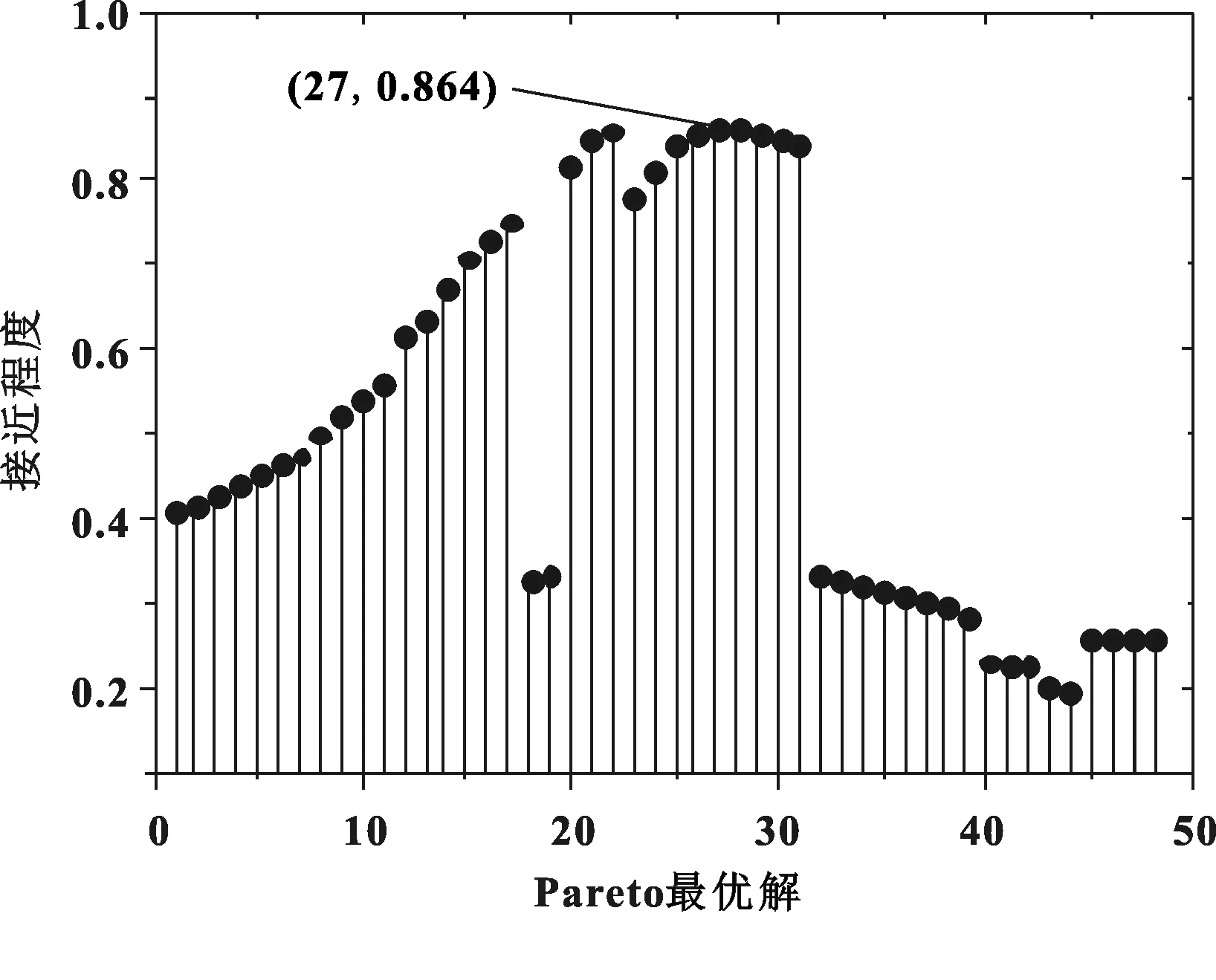
图8 基于熵权TOPSIS方法获得的Pareto前沿接近程度

表5 优化方案性能对比

4 结论

文中以某车型后排座椅为研究对象，采用NSGA-II优化算法结合RSM-RBF混合近似模型和基于熵权TOPSIS方法对其进行结构-材料一体化多目标轻量化设计研究，取得如下结论：

(1)采用RSM-RBF混合近似模型对非线性程度较高的多响应问题有较好的拟合精度，除了个别零件响应值的精度稍低以外，其余目标精度都在0.85以上，满足要求。

(2)采用基于熵权TOPSIS方法选择的最佳折中解不仅与仿真模型误差小，而且在座椅总质量和安全性能之间得到了适当的平衡。

(3)在满足座椅行李箱碰撞试验相应法规要求的同时，使得座椅总质量降低16.73%，轻量化效果明显，部分优化部件应变指数有所上升，但仍在安全范围之内。