曲线拟合最小二乘法的案例式教学探索

李珍珍

【摘要】曲线拟合最小二乘法是工程实践和统计研究中常用的一种数据处理方法，本文为提升学生的学习效果采用案例式教学法，首先给出一个教学案例，通过案例分析，引出曲线拟合最小二乘法的一般原理，再给出练习题来加强学生对最小二乘法的理解.

【关键词】计算方法;曲线拟合;最小二乘法;案例教学

计算方法又称数值分析，是理工类本科和研究生的一门重要课程，主要为工程计算中出现的各类数学问题提供适合计算机处理的算法，并进行误差分析.该课程的特点是需要扎实的基础知识;内容多，理论性强;实践应用性强[1].在传统的讲授型教学过程中我们发现学生学习兴趣不大，学习效率不高，学习效果不佳，因此需要探索更加有效的教学方法.案例式教学模式是基于教学目标的要求，依托案例，由教师引导学生学习、研究以及提升能力的教学方法[2].本文以曲线拟合的最小二乘法为例，进行案例式教学探索，旨在激发学生的学习兴趣，提升教学效果.

一、提出案例

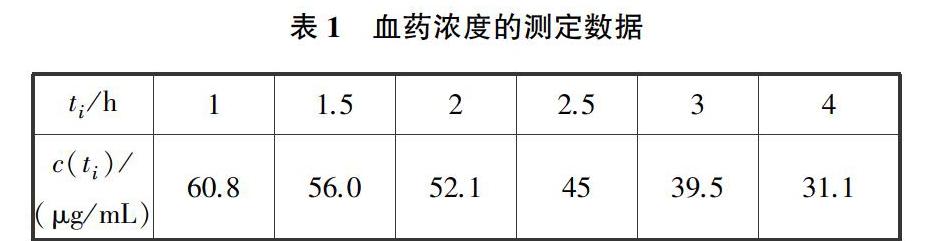
在教学中教师首先提出给药案例：假设向患者静脉注射某种药物300 mg剂量，在ti h后测得血药浓度c（ti）μg/mL如表1（一组虚拟数据）所示，i=0，1，2，3，4，5.

為保证药物的疗效，血药浓度应保持在最小有效浓度25 μg/mL以上.请预测：当给药多久后，血药浓度会下降到25 μg/mL？

二、案例分析

表1中的血药浓度c（ti）是通过测量得到的，其本身具有一定的测量误差，如果用这组数据通过插值法得到插值多项式，那么该插值多项式保留了这些误差，不符合原有规律，因此考虑寻找一个简单函数，使其曲线不必经过所有数据点，但尽可能接近每个数据点，这类问题称为曲线拟合问题，这个简单函数称为拟合函数.

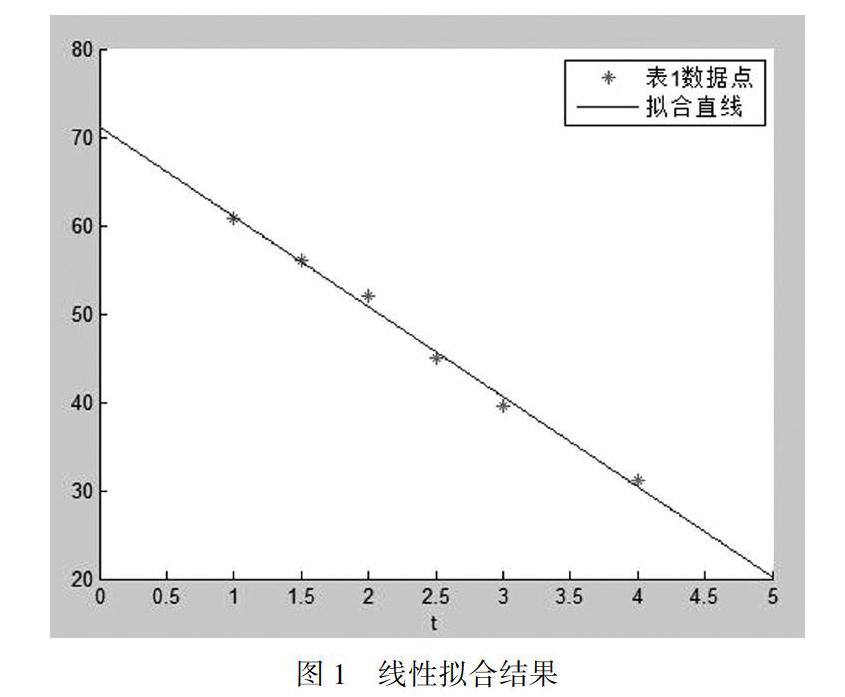
为了找到这个简单函数，将表1中的数据在坐标系中标出来（见图1）.根据图1数据点的分布情况，考虑用直线拟合这组数据，即选{1，t}作为基函数，求线性函数p（t）=a+bt，其中a，b是待定参数.为使p（t）的图形尽可能接近每个数据点，我们令∑5[]i=0（p（ti）-c（ti））2最小，即寻找a，b使函数

将上述用直线拟合的思路拓宽，我们也可以选曲线拟合，最简单的是拟合函数采用n次多项式，比如多取一个基函数t2，则拟合函数为p=a+bt+ct2.

更一般地，若只知函数y=f（x）在离散点x0

求解上述线性方程组可得系数a0，a1，…，an的值.

另外，有时根据数据点的分布，选择的拟合函数是关于待定参数的非线性函数，比如s（x）=aebx，按照使s（x）与f（x）在各离散点处误差平方和最小的原则，用极值原理建立的法方程组是关于待定参数的非线性方程组，这类数据拟合问题称为非线性最小二乘问题[3].

四、练习题

某县水库上游河段降暴雨，根据测算在ti h上游流入水库的流量Q（ti）（102 m3/s）如表2，试用最小二乘法拟合表中数据.

五、结束语

与传统的理论讲授相比，课堂上首先提出教学案例，更能引起学生的学习兴趣，案例分析能充分调动学生的学习积极性，接下来能让学生更好地理解曲线拟合的最小二乘法，另外，增加课堂练习题可以提高学生分析问题、解决问题的能力.

【参考文献】[1] 江志超，邓凤茹，毕晓华，等.案例教学法在研究生数值分析课程教学中的应用研究[J].北华航天工业学院学报，2017（06）.

[2] 钱旭.“计算方法”课程“案例-任务驱动”的立体化教学模式探索[J].新课程研究，2017（06）：105-107.

[3] 同济大学计算数学教研室.现代数值计算（第2版）[M].北京：人民邮电出版社，2014.