基于粒子群优化算法和离散小波变换的心电信号去噪算法

邓一凡

（华北电力大学，北京102200）

心电图（Electrocardiogram, ECG）是对心脏多个心动周期产生的电活动变化的图像记录，是通过将电极放置于体表实现的。心电图常用于帮助医生们诊断心律失常、心肌梗塞等心血管疾病。在心血管疾病中，心律失常是最常见的，因此对心律失常的精准分类一直是生物医学研究的热点。医生们通过人工对心电图进行分析，不仅耗时耗力，还容易因为疲累对最后的疾病诊断产生不良影响。因而通过人工智能实现的心电信号分类算法不仅可以帮助医生分担压力，也能够提高疾病分类的准确率。

心电信号在采集的过程中容易受到环境和设备等因素的影响，导致采集到的心电信号受到噪音的污染。这些噪音主要被分为三类：（1）来自50hz 交流电的工频干扰，（2）来自肌肉的收缩和颤动的肌电干扰，（3）来自人体自身呼吸的基线漂移。传统的心电信号去噪方法是数字滤波，包括低通滤波器、高通滤波器和带陷滤波器等。但是，三类噪音很难用一种数字滤波器滤除，因此通常需要共同使用多个数字滤波器。而且数字滤波属于线性滤波，在滤除噪声的同时，它们很可能会导致信号的奇异点改变或者信号的边缘模糊不清的后果。

由于心电信号是一种不平稳的信号，在时域和频域非常多变，波形的变化也不可预测。而小波变换具有优异的时频分析和局部性分析特性，因此小波变换被广泛应用于信号处理上。研究员早已经把小波变换应用于心电信号的降噪中，并且小波变换已经成为心电信号去噪最有效的方式之一。Donoho[1,2]提出了一维和二维信号的小波阈值去噪方法。Sayadi 等人[3]提出了一种新的基于小波变换自适应阈值的ECG 降噪方案bionic-WT（BWT）。Novak 等人[4]提出了一种基于小波变换的不同噪声水平检测算法的去噪方法。Singh 等人[5]提出了一种小波域中去除心电噪声的母小波基函数选择方法。

小波变换的参数选择之间影响到最后的滤波效果。本文提出用粒子群优化算法对离散小波变换的参数进行优化，从而找到使原始心电信号和去噪信号均方差最小的小波去噪参数，即最佳参数。

1 离散小波变换

表1 小波变换参数范围表

小波变换是一种强大的时频域处理工具，已经被成功应用于心电信号的处理中，解决心电信号去噪、特征提取等问题。小波变换有五个参数：（1）小波基函数类型；（2）分解层数；（3）阈值函数；（4）阈值选择规则；（5）阈值重缩放方法。这五个参数的取值范围如表1 所示。

小波变换主要包括连续小波变换（CWT）和离散小波变换（DWT）[6]。本文主要使用离散小波变换。DWT 通过使用一组滤波（即低通和高通滤波器）来分解信号，以分别产生近似系数cA和细节系数cD。假设原始心电信号有n 个样本，x(t)=[x(1)，x(2),…,x(n)]。假设将心电信号分为L 个层次，每个层次分解为两部分，即近似系数（cA）和细节系数（cD）。cD 将使用高通滤波器进行处理，而cA 将继续进行下一级的分解。使用DWT 的主要目的是通过不同的系数级别对输入信号进行分解，以校正输入信号的高频[7]。Matlab 提供了几种通过DWT 进行信号分解的方法。此外，Matlab 还提供了一种应用逆离散小波变换（iDWT）的信号重构技术。

本文将用小波变换完成心电信号的分解，再利用逆小波变换（iDWT）完成对心电信号的重构。

小波去噪过程可分为三个阶段：

第一阶段是心电信号的分解阶段，该阶段我们首先需要选择第一个参数即合适的小波基函数用于分解心电信号，然后选择第二个参数分解层数L。

第二阶段是阈值的选取，需要同时选择阈值函数类型、阈值选择规则和阈值重缩放方法这三个参数。小波提供了两种标准的阈值函数，分别是软阈值函数和硬阈值函数。阈值通常基于噪声幅度的标准偏差(σ)来定义[8]。阈值规则根据公式（1）选取。

其中x（n）是原始ECG 信号，e 是噪声，σ 是噪声的幅度，n是样本数。小波参数（β、λ 和ρ）必须分别应用于每个小波系数（近似和细节）级别。

第三阶段是通过逆离散小波变换（iDWT）实现去噪后的心电信号的重构。如公式（2）所示。

2 粒子群优化算法

式中，Gk表示最大迭代次数。Wini为初始惯性权值，Wend为迭代至最大进化代数时的惯性权值。

3 基于粒子群优化算法和小波变换的心电信号去噪方法

本文提出的心电信号去噪方法有以下三个阶段：

第一阶段：包括输入心电信号和。首先读入原始心电信号，然后添加高斯白噪音，再计算心电信号的信噪比SNR、均方根差PRD 和均方误差MSE。接着初始化五个小波变换的参数：小波基函数，分解层数，阈值函数，阈值选择规则和阈值重缩放法。小波变换参数取值范围见表1。同时初始化粒子群优化算法的参数，粒子群优化算法初始化参数值如表2 所示，其中D 表示维度，N 表示群规模，G 表示最大迭代次数，w代表惯性权值。

表2 粒子群优化算法初始化参数值表

第三阶段：利用最佳小波参数对心电信号去噪。主要包括以下三步:基于离散小波变换的心电信号分解、阈值选取和基于逆离散小波变换的心电信号重构。

4 结果与讨论

本文选取了MIT-BIH 数据库作为实验数据。该数据库是由美国麻省理工学院与Beth Israel 医院联合建立的研究心律失常的数据库，它也是目前在国际上应用最多的数据库。每条心电图记录有650000 个采样点，采样率为360 Hz，分辨率为10 mV范围内的11 位，比特率为3960 bps。实验设备配置为：戴尔G3、intel core i7、RAM 8G、MATLAB R2014a。为了评价系统的降噪性能，采用了均方根差PRD 和信噪比SNR 两个指标。信噪比是输出信号功率与输出噪声功率的比值，信噪比越大，说明输出信号中的噪音越少。均方根差PRD 和信噪比SNR 分别根据方程（7）和方程（8）计算。

其中，x(n)表示使用过基于粒子群优化算法的小波变换去噪算法的心电信号，N 为采样点。

本文使用基于粒子群优化算法的小波变换去噪算法对MIT-BIH 数据库中的48 条心电信号数据进行了测试，我们对原始信号加入高斯白噪声，使输入信噪比为0-30dB 后，再使用本文提出的心电信号去噪算法对加噪信号进行去噪，并计算了信号去噪前后信噪比SRN 和均方根差PRD 的平均值。如表3所示，均方根误差随着输入信噪比的增加而减小。在选择小波基函数时，Daubechies 函数和Symlets 函数被选择得较多，分别是三次和两次。而且Daubechies 函数总是在信噪比较高的范围内被选择。从分解层数来看，低信噪比适合的分解层数范围为5至7 层，而高信噪比适合的分解层数范围为2 至4 层。该算法选用的阈值函数是软阈值函数，原因是硬阈值函数可能会引起信号的不连续性。阈值选择规则主要集中在Heursure 和Rigsure两个选项之间，其中Rigsure 被选择得更多。最后，在所有阈值重缩放方法中，sln 取得了绝对性优势。表4 给出了基于粒子群优化算法和离散小波变换的去噪算法对输入信噪比为0 到30 dB的心电信号的评估效率。由表3 可见，经过心电信号去噪算法去噪的心电信号信噪比均提高了，说明本文提出的心电信号去噪算法能够有效去噪。且随着输入信噪比的升高，另外，PRD 的变换表明该方法对信号的去噪比较平稳，特别是当心电信号具有低噪声时。PRD 的降低表明了本文所提出的基于粒子群优化算法和离散小波变换的心电信号去噪算法的有效性。

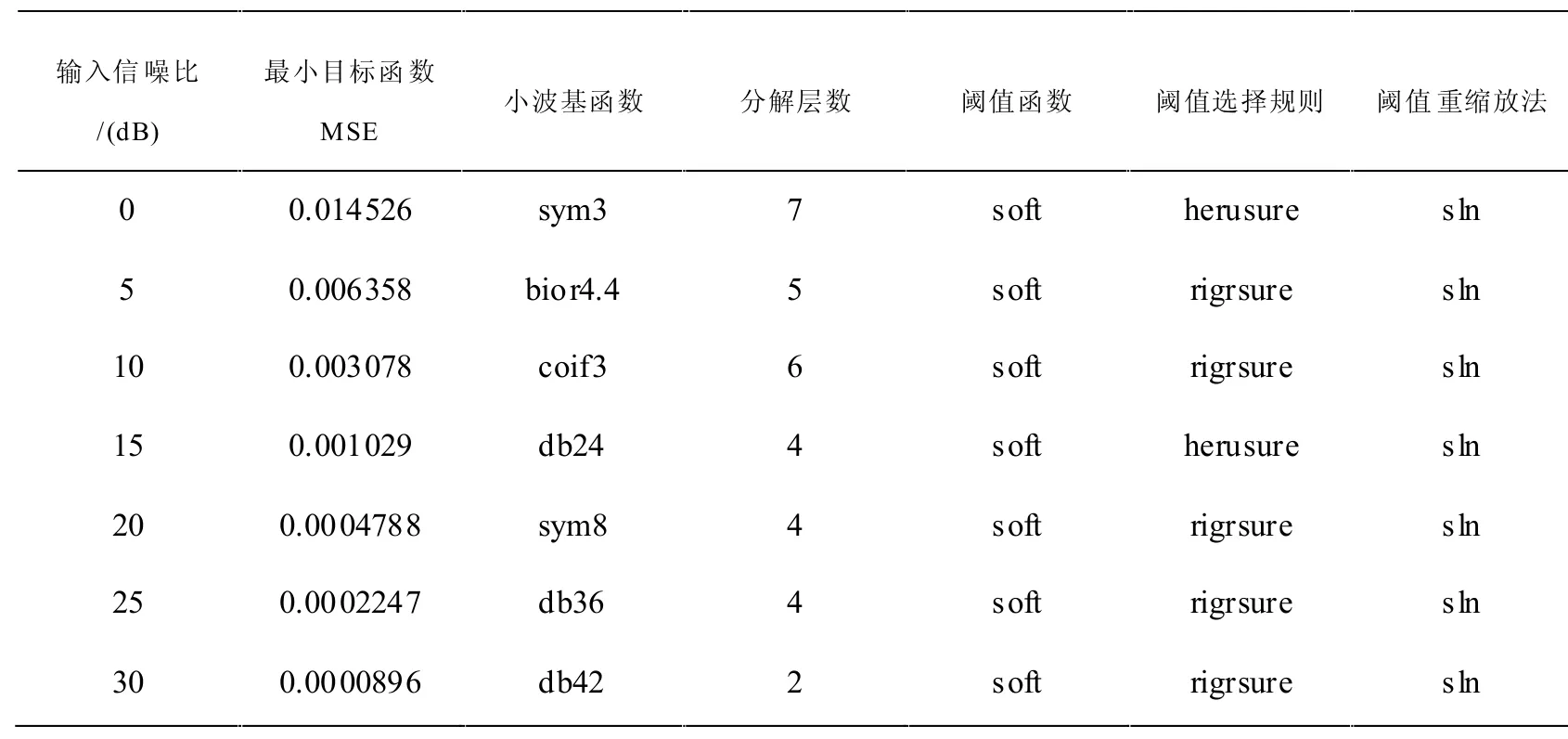
表3 用粒子群优化算法获得的最佳小波变换参数

表4 不同信噪比输入对心电信号去噪性能的影响